循环流化床锅炉炉膛流动特性数值模拟进展
杨 照,刘雪敏,张肖阳,齐国利,董 勇
(1.山东大学 燃煤污染物减排国家工程实验室,山东 济南 250061; 2.中国特种设备检测研究院,北京 100029)
炉膛内的流动特性是循环流化床锅炉(CFBB)燃烧反应和传热的基础,具有重要的研究价值和意义,并得到了充分的研究[1-4]。整体和局部流动结构的不均匀性是炉膛气固两相流动最显著的特征,根据已有的研究,炉膛整体由底部高固体颗粒体积分数的密相区和上部低固体颗粒体积分数的稀相区组成,孔隙率分布呈现为轴向的S型结构和径向的环-核结构,而炉膛局部颗粒则处于不断地聚集和分裂状态,具有团聚趋势。
然而实验方法存在研究成本高、获得数据有限等不足,尽管测量工具和研究方法随着科技进步得到了一定的发展,但截至目前,炉膛内的许多关键参量或是难以通过实验测得,或是存在一定的局限性。例如炉膛中的压力尚可通过实验测得,固体体积分数也可以通过所测的压降推导,但所得数据仅能反映某一高度或某一时刻的特定物料体积分数。因此,数值模拟方法受到了越来越多研究者的青睐。
笔者分析了近10 a炉膛流动特性模拟研究的进展,重点分析了炉膛流动特性模拟的关键因素——曳力模型,对模拟中多相流模型和曳力模型的耦合进行阐述,分析当前研究存在的不足,探讨未来CFBB气固两相流动模拟的发展方向。
1 炉膛流动特性模拟研究进展
炉膛内固相的流态化现象是CFBB最典型的特征,模拟须从气固多相流模型入手。
根据对固相的描述,目前已有的多相流模型分为基于欧拉-欧拉(E-E)方法的双流体模型(Two Fluid Model,TFM)和基于欧拉-拉格朗日(E-L)方法的离散元(Discrete Element Model,DEM)模型以及计算颗粒流体力学(Computational Particle Fluid Dynamics,CPFD)模型。E-E方法基于连续介质假设(亦被称为连续介质模型),将流体与离散的固相作为共同存在且相互渗透的连续介质;E-L方法则只将气体相当作连续相,分别在欧拉坐标系和拉格朗日坐标系下描述气相和固相。E-L方法中,DEM模型充分计算固相间的力和碰撞,详细描述颗粒运动,能够揭示颗粒相的宏观流动特性和确定固相在系统内的停留时间;CPFD模型基于MP-PIC(Multi-Phase Particle In Cell)[5]方法,引入颗粒碰撞模型和空间梯度来计算固相间的相互作用力和碰撞,并将一部分位置、速度相近且粒径、密度等物理量相同的颗粒作为整体进行计算[6-7]。
相较于实验,模拟可以捕获更详细的流动细节,并提供可视化的结果,有助于理解整个系统内的气固流动行为。目前已有许多研究者通过模拟得到了炉膛的典型流动特性,证明了模拟的可信程度。
LIU等[8]和ZHANG等[9]在采用TFM模型的CFBB全回路模拟中,捕获了炉膛内固相下浓上稀的分布特点,得到了炉膛内 “下浓上稀”和径向“环-核”的分布特征(图1);NIKOLOPOULO等[10]在研究中进一步将炉膛分为底部密相区域、中部飞溅区域和顶部自由发展区域3个区域(图2)。而WANG等[11]在采用DEM模型对实验室规模的CFBB全回路的模拟中除了捕获了炉膛固相轴向S型分布(图3)外,还发现湍流现象贯穿整个炉膛,团聚主要在炉膛底部壁面附近形成(图4)。

图1 CFB锅炉内固体体积分数Fig.1 Solid volume fraction distribution in CFBB
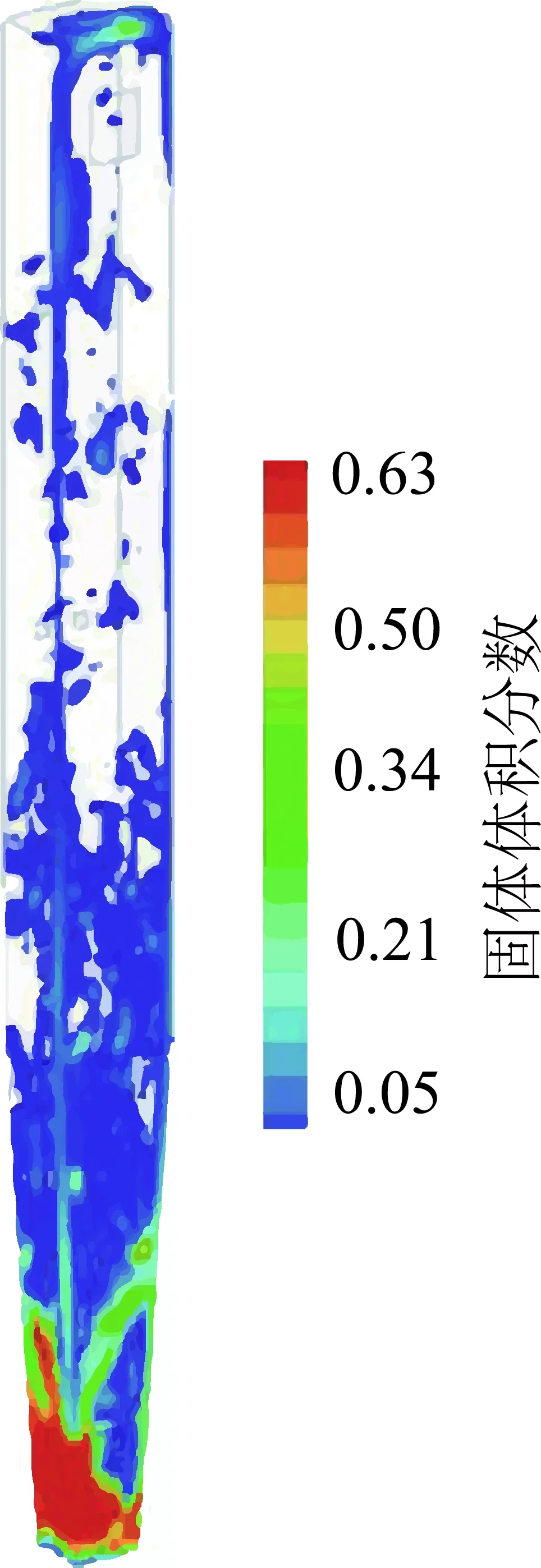
图2 炉膛内固体体积分数[10]Fig.2 Solid volume fraction in furnace[10]
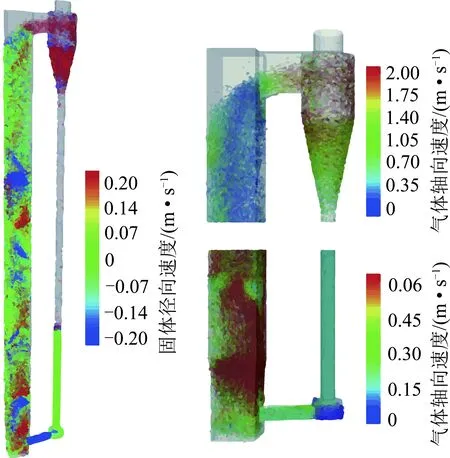
图3 CFB中固体瞬态运动[11]Fig.3 Transient motion of solid phase in CFB[11]

图4 炉膛内固体运动及分布Fig.4 Movement and distribution of solids in furnace
除了能直观地反映炉膛内的宏观流态特征外,通过模拟还能捕获颗粒详细的运动轨迹,用以研究系统内固相的微观流动特性。
LUO等[12]和WANG等[13]在采用DEM模型的CFBB模拟中观察到了强烈的固相返混现象,且主要发生在炉膛壁面和角落处;FANG等[14]进一步将炉膛内固相的混合过程分为启动阶段、迁移阶段、强烈混合阶段和稳定阶段4个阶段,并发现对流混合、剪切混合和扩散混合分别主要发生在炉膛的下部、中部和顶部,固相轴向扩散在整个区域中占主导地位。LUO等[12]还根据炉内固相平均速度捕获了炉膛中心区域的固相向上运动和壁附近的固相向下流动,并将炉膛底部粒子无序运动的原因归为固相反混、回料阀回流、流化风和粒子间相互作用。WANG等[15]还发现固相速度在炉膛中心区域和4个角处较大,而在环带区域中较小(图5)。

图5 炉膛局部区域固体速度[15]Fig.5 Solid velocity in the local area of furnace[15]
模拟方法还能提供炉膛内更为详细的物理参数,通过研究参数的动态变化过程,有助于加深对炉内气固流动行为的理解和认识。
曾胜庭等[16]在300 MW CFBB的 CPFD 模拟中,根据炉膛内的固相体积分数和颗粒速度分布证实了密相区后墙壁面附近存在的床料富集现象,并发现固相体积分数分布随着炉膛高度的增加而逐渐降低,稀相区内的床料分布更为均匀,部分床料颗粒在气流曳力的作用下被携带上升,另一部分贴近壁面的颗粒则呈现下降的流动状态。李德波等[17]在300 MW循环流化床锅炉的CPFD模拟中,根据炉膛速度矢量图发现,炉膛密相区中部气流速度在一次风和部分沿壁面返回风量的作用下大幅增加,同时壁面处出现数个中心区域速度极低的旋流,炉膛底部前壁处的颗粒体积分数较其他处更高。张瑞卿等[18]在采用CPFD模型的工业示范循环流化床锅炉炉膛模拟中研究了炉内的物料体积分数,研究表明,固相物料体积分数在炉膛边壁处存在明显的上升趋势,在炉膛下部中心区出现明显的体积分数峰值,而体积分数峰值并没有在炉膛顶端中心区出现。JIANG等[19]在对具有六旋风分离器布置的大型CFBB的CPFD模拟中研究了炉膛内的气相速度场,观察到炉膛出口处的气流速度矢量方向从垂直转变为水平,炉膛底部气流具有向上和向下流动的不均匀性,中心处固相的垂直速度高于壁面处的颗粒。另外,实验研究中用于定义炉内流态的物理参数通常局限于空隙率、气固滑移速度和方向,而通过数值模拟研究,有可能利用更详细的物性参数完善对炉内流态的定义。TU等[20]采用CPFD多相流模型模拟了带有6个旋风分离器的CFBB,并根据压力时间序列等参数确定了炉膛中随着表观气速增加而出现的3种流态,即多气泡流态(Multiple Bubble)、鼓泡流态(Bubble Regime)和湍流流态(Turbulent Fluidization Regime)。
总而言之,通过数值模拟方法研究炉膛内的流动特性,研究者们已获取更详细的流动细节和可视化结果,加深了对炉膛内气固两相宏观和微观流态特征的认识,有助于完善炉内气固两相流态的定义,并会在今后的模拟研究中不断深化对流动特性的认知。
2 炉膛流动特性数值模拟的关键模型
颗粒间的碰撞只是气固两相流模型需要处理的问题之一。研究证明,相对于对固相的准确描述,气固两相流模拟的关键在于系统中气体-粒子和粒子-粒子相互作用的正确表达[21-23]。曳力作为多相流动中最重要的相间相互作用,决定了炉膛内的气流对颗粒的夹带和输送以及内循环流动等行为[24-26]。因此,无论是E-E法或E-L法,曳力模型都是决定数值模拟准确性的关键。
作为多相流动中最主要的相间相互作用,针对曳力已建立了大量的模型。目前曳力模型主要可以分为传统均匀曳力模型、关联型曳力模型和极值型曳力模型3类[27-29],表1对现有的曳力模型进行了归纳。

表1 曳力模型的分类Table 1 Classification of drag model
复杂系统中的介尺度关联着微尺度和宏尺度,在CFBB系统中,微尺度、宏尺度和介尺度分别指颗粒尺度、设备尺度和颗粒团尺度。
研究表明,炉膛内的固相趋向保持最小重力势能,处于不断地聚集、形成团聚并分裂的状态;气相则趋向于选择阻力最小的路径,倾向于绕过而非穿透颗粒团[63-64]。2种运动机制之间的相互协调得到稀、密相共存的稳定性条件,并实现了流动优势的折中[65],造成了炉膛内流动的复杂性和多样性。同时,由于炉膛内的主要流动曳力来自密相团聚体内部及其界面,因此炉膛内的有效气固动量交换低于均匀悬浮液[57]。
综上所述,介尺度结构是导致炉膛气固流动结构非均匀性分布的根本原因,研发曳力模型的重点在于考虑介尺度结构和系统中固相的异质空间分布对曳力的影响[66-67]。
2.1 均匀曳力模型及关联型曳力模型
均匀曳力模型的构建基于单颗粒曳力模型和均质系统(固定床或均匀液固流化床)的实验结果,采用平均化方法对曳力系数进行修正,并应用于CFBB多颗粒体系模拟。但平均化方法简化和忽略了炉膛多尺度结构的复杂性,会高估气固相之间的曳力[68-69],更适用于颗粒体积分数较低、气固流动较为均匀的体系。
基于建立新曳力模型的困难和均匀曳力模型捕获气固两相基本特征的能力[70],研究者们试图通过修正均匀曳力模型以获得能够用以描述介尺度的次网格模型,即关联型曳力模型[27]。根据对均匀曳力模型的修改依据可以将关联型曳力模型分为修改颗粒直径法、细网格归纳法和修正曳力系数法3类。
修改颗粒直径法将颗粒团当成一个整体,增大直径的颗粒被当作颗粒团以考虑颗粒趋于成团的流动特性。采用修改颗粒直径法的前提是准确描述颗粒团聚现象,但炉膛内的颗粒团受到气相和固相的性质、炉膛的几何形状和运行条件等因素的影响,导致该方法不具有普适性,实用性和准确性也有待深入研究。
细网格归纳法从概念上将一个复杂的多尺度闭合模拟任务分解为解决描述微尺度和介尺度的任务,采用传统曳力模型对炉膛内的微小区域进行高精度模拟,通过求解区域内参数的时间平均得到适用于粗网格模拟的曳力模型,但其本质依然是均匀曳力模型。
修正曳力系数法通过修正均匀曳力模型中的曳力系数,减小均匀曳力模型对于曳力的估计,根据修正方法的不同可以分为直接修正方法和经验修正系数法2类。直接修正方法即通过给曳力模型添加一个小于1的系数减小曳力,缺点在于曳力系数的修正需要大量试算,且修正值取决于研究者的主观意愿,缺乏完善可靠的理论依据;经验修正系数法以O’BRIEN和SYAMLAL[54]提出的O-S模型为代表。O’BRIEN和SYAMLAL基于FCC系统实验数据提出了颗粒团聚效应的修正公式,并以此修改均匀模型曳力参数,保障了模型的准确性。但由于需要根据模拟对象进行广泛的研究而缺乏普遍性,O-S模型通常作为检验曳力模型的基准。
均匀曳力模型和O-S曳力模型的曳力函数分布如图6所示(其中,β为单位体积的曳力系数。定义为β=εgnsFD/ur,其中εg为气体体积分数,ns为颗粒数密度,FD为颗粒所受曳力,ur为气固相对速度[61])。图6(a)汇总了部分均匀曳力模型,由图6(a)可知,不同均匀曳力模型的曳力曲线几乎完全重合,曳力随颗粒体积分数增加而单调增大,没有体现出非均匀流动中因介尺度的存在而导致的曳力降低。由图6(b)可以看出, O-S曳力模型预测在颗粒体积分数εs=0.01~0.50内非均匀流的曳力会发生显著的降低,且在εs≈0.10时曳力下降幅度最大,炉膛稀、密相两侧的流动趋于均匀,符合实验现象[71]。

图6 均匀曳力模型与O-S曳力模型对比[28,71]Fig.6 Comparison of homogeneous model and O-S drag model under different Gs[28,71]Fig.6 Comparison of homogeneous model and O-S drag model Gs[28,71]
2.2 极值型曳力模型
极值型曳力模型以EMMS模型为代表的非均匀曳力模型。EMMS曳力模型基于“多尺度最小能量理论”(Theory of Energy Minimum Multi-scale,EMMS),核心在于对介尺度结构和多结构折衷特性的描述[72],炉膛非均匀区域被分为“颗粒密相”、“颗粒稀相”和“相互作用相”3个均匀的子系统,通过稳定性条件(单位质量颗粒的悬浮输送能耗Nst趋于最小)描述介尺度上两种主要趋势的折衷[73]。
原始EMMS模型由李静海等提出[57],最初被应用于稳态气固流动和结构效应的量化[60],仅考虑了重力对曳力的影响。
而后,杨宁等[58-59]考虑了颗粒的平均加速度和曳力、重力的不平衡,建立了Y-EMMS模型。Y-EMMS将颗粒局部加速度纳入考虑,能求解特定工况下的曳力系数,但模型中包含经验公式,且忽略了气固两相流速对曳力的影响。
随后,王维[60]进一步引入稠密相、稀相和相间的惯性加速用以区别稀、密相内部颗粒加速度,建立了EMMS/matrix模型。EMMS/matrix模型采用2步EMMS分析法,首先对循环流化床的操作参数进行最小能量分析得到颗粒团参数关于气体体积分数的关系式,然后将关系式与CFD耦合得到非均匀曳力修正系数,综合考虑了操作参数和局部流动参数对曳力的影响。但该模型密相颗粒的受力表达式并未采用实际的受力分析。
后续,祁海鹰等[28]基于颗粒团密度εsc修正了颗粒团直径,通过完善局部颗粒的受力平衡提出了不含经验系数的QL-EMMS模型和QL-EMMSn模型[61]。在祁海鹰等的基础上,陈程等[62]进一步引入非均匀因子和基于整体气固滑移速度的状态雷诺数提出了QC-EMMS模型,实现了曳力模型的流动自适应,但该阶段模型尚未考虑颗粒尺寸分布。
EMMS曳力模型的对比如图7所示。EMMS曳力模型在一定局部体积分数范围内都预测到了不同程度的曳力下降,Y-EMMS模型预测的曳力系数在空隙率0.7~1.0内会大幅降低, EMMS/matrix模型预测曳力系数在除了炉膛两端外的大部分空隙率范围内都会降低,QL-EMMS曳力模型预测曳力在εs=0.01~0.35内显著下降。

图7 不同曳力模型对比[77]Fig.7 Comparison of different drag model[77]
但EMMS模型曳力函数随颗粒体积分数的变化趋势与基于实验的相对准确可靠的O-S模型相比,或包含没有物理意义的转折,或存在不同的变化趋势,原因主要在于对颗粒团直径预测的缺陷[74-77]。
合理描述颗粒团特性的QC-EMMS模型能够体现非均匀流曳力随颗粒体积分数呈“凹状”上升,且在稀、浓两端趋于均匀态的非均匀流曳力下降的本质特征(图8)。

图8 QC/QL-EMMS模型与O-S模型的对比[62]Fig.8 Comparison of QC/QL-EMMS model and O-S model[62]
决定CFBB炉膛内两相流模拟成败的关键和未来研究的重点仍是曳力模型[78]。采用均匀曳力模型、关联型曳力模型将导致低估炉膛(提升管)底部稠密区域中固体的体积分数和高估颗粒循环流率,无法捕获颗粒动态集群的形成和消失等特性[58],且即使在采用高网格密度的前提下仍然不能实现本质上的改变[79]。而EMMS曳力模型捕获炉膛(提升管)内非均匀结构的能力更强,可以明显区分和预测炉膛(提升管)内的稀相、密相区域及异质结构[20,80]。
现有的EMMS曳力模型均未考虑颗粒粒径的宽筛分特性,且目前用以检验的O-S模型基于FCC系统实验数据而非CFBB系统,同时研究炉膛内的气固流动特性时需考虑各部件之间的相互影响。因此,现有的曳力模型还需要进一步改进以适用于CFBB全回路多流态的模拟。
3 模型的耦合与选择
尽管多相流模型通常被认为仅对模拟结果产生次要影响[81],但出于科学的严谨性考虑,在CFBB的模拟中考虑多相流模型和曳力模型的耦合对于模拟结果的影响十分必要。考虑到CFBB属于CFB的应用之一,而目前针对CFBB的模拟相对较少,因此对近20 a CFB模拟中采纳的多相流模型、曳力模型及模拟对象和颗粒类型进行了归纳(表2~4)。

表2 基于TFM多相流模型的CFB模拟Table 2 CFB Simulation based on TFM model
固体颗粒依据颗粒粒径和与流体密度之差可以分为 A,B,C,D 四类。CFB锅炉系统中,A类颗粒飞灰仅在炉膛中短暂停留, B类颗粒作为外循环回路的主要成分将直接影响流动情况,故CFBB模拟的颗粒类型将以B类颗粒为主。
TFM模型和均匀曳力模型或EMMS曳力模型耦合是目前被采纳最多的方法。相比于与均匀曳力模型耦合,TFM模型与EMMS的耦合基于EMMS稳定性条件约束,能更准确预测流态,是目前准确性最高的模拟方法;模拟对象多为化学链燃烧(CLC)装置、气化炉和碳酸化器等小型/中试CFB提升管的研究,应用于大型CFB全回路模拟的研究较少;涉及的颗粒类型主要是A类和B类。但TFM模型基于连续介质假设,导致难以实现粒径分布[60,105]和缺乏尺度分离[106-107],同时出于计算机性能考虑而简化了计算[108-110],与真实情况存在一定差异。

表4 基于CPFD多相流模型的CFB模拟Table 4 CFB Simulation based on CPFD model
DEM模型在详细追踪颗粒运动的同时增加了计算压力[97],因此多与均匀曳力模型耦合并应用于小型循环流化床的模拟,涉及的颗粒类型主要为粒径较大的D类颗粒,不适用于CFB锅炉的模拟。
CPFD模型兼备处理宽筛分、多粒径的颗粒负载情况和追踪单个颗粒、处理多分散颗粒群的能力,目前多与均匀曳力模型耦合,并被大量应用于B类颗粒和大型CFB系统的模拟,同时由于CPFD模型能够模拟非流化颗粒的运动而被不少研究者应用于立管、返料阀等设备的研究。相较于完全依赖网格精度的TFM模型和大量追踪粒子运动的DEM模型,CPFD模型兼备高效率和准确性,更适用于CFB锅炉的模拟。
CPFD模型目前主要的不足在于对曳力把握的不准确,但目前CPFD模型多与均匀曳力模型耦合,且因为高估曳力而产生误差[24,78,111]。而将CPFD模型与EMMS模型耦合则能够解决CPFD模型高估曳力的问题,能够获得更准确的模拟结果[100];同时CPFD模型中考虑了颗粒粒径的宽筛分特性,得以弥补当前EMMS曳力模型的不足。EMMS曳力模型CPFD模型与EMMS模型耦合的方法在理论上兼顾对气固两相分布和气固、固相之间作用力的准确描述,同时还优化了数值计算效率,具有很高的应用前景。
4 结 论
(1)数值模拟能提供更详细的流动细节和可视化结果,加深了对炉膛内气固两相宏观和微观流态特征的认识,根据炉膛内气固两相详细的物理参数能完善对炉膛内流态的定义。
(2)曳力模型是影响炉膛流动特性数值模拟的关键。曳力模型可分为均匀曳力模型、关联型曳力模型和极值型曳力模型:均匀曳力模型忽视了介尺度和微尺度不均匀结构的影响,并将高估气固间的曳力系数;关联型曳力模型基于均匀曳力模型,无法从本质上解决均匀曳力模型高估曳力的问题;EMMS极值型曳力模型有效解决了介尺度的问题,并在近年得到了不断的优化和改进,是目前最好的曳力模型。但由于炉膛内气固流动的复杂性及各部件之间的相互影响,目前的曳力模型仍存在不足,有待于建立符合炉膛流态的且适用于CFBB全回路系统的多流态曳力模型。
(3)目前大多采用EMMS模型与TFM模型耦合。然而TFM模型对固相的描述不够准确,无法捕捉流态的本质特征;相比较而言,CPFD模型对于多相流的模拟要更加优越,发掘新的流动特性的可能更高。因此将EMMS曳力模型与CPFD多相流模型耦合是一种很有前景的循环流化床模拟方法,在未来会被更多研究者采用。

