多层叠置煤层压裂裂缝纵向扩展模型与数值模拟

杨兆中，张 丹，易良平,2，李小刚，李 宇

(1.西南石油大学 油气藏地质及开发工程国家重点实验室，四川 成都 610500; 2.西南石油大学 机电工程学院，四川 成都 610500; 3.中海油能源发展股份有限公司，天津 300452)

鄂尔多斯盆地东缘临兴、滇东黔西等地区，煤层纵向叠置，具有多层、薄层、层间距小等特征，不同煤层的压力系数和渗透性质差异明显[1-8]。这类地层中压裂缝高的合理控制对煤层气有效开采非常重要。

关于水力裂缝的纵向延伸问题，国内外运用物理实验和数值模拟开展了大量研究。物理实验表明，水力裂缝纵向扩展受层间应力差、弹性模量、界面强度、压裂液黏度等因素的影响，其中层间应力差为主要影响因素[9-16]。目前常用的裂缝纵向扩展数值模拟方法有边界元法[17]、有限差分法[18-20]、位移不连续法[21-22]、有限元法[23-25]和扩展有限元法[26]。这些方法在模拟裂缝延伸时需要预设裂缝扩展步长，且需要建立相交准则来判断裂缝扩展至界面后的延伸方向。而基于损伤力学建立的裂缝延伸模型则不需要预先设定裂缝延伸方向和相交准则，在处理裂缝延伸问题时不需要额外的规则来描述裂缝界面，裂缝延伸后不需要重新剖分网格。因此，笔者基于损伤力学建立了水力压裂裂缝纵向扩展流固耦合计算模型，基于该模型模拟多层叠置煤层中水力裂缝纵向延伸规律，分析多层叠置煤层压裂缝高的影响因素。

1 模型建立与求解

1.1 损伤演化模型

当材料受到单轴拉伸时可以将其损伤演化法[27]则表示为

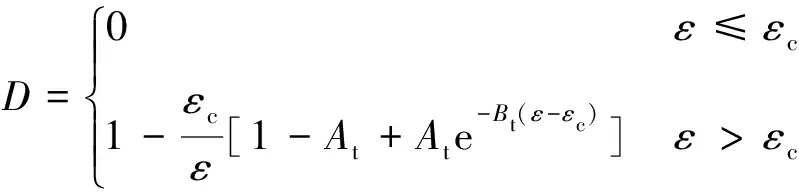
(1)

式中，D为损伤变量;ε为应变；εc为临界应变(材料开始破坏时的应变);At,Bt为材料拉伸系数。

1.2 控制方程

若忽略惯性力和体积力的影响，将饱和流体的多孔介质视为线弹性材料，则多孔弹性岩石的控制方程[28]为

(1)应力平衡方程:

∇σ=0

(2)

式中，σ为总应力张量，Pa。

对于完全饱和的多孔介质，根据孔弹性力学理论[29]，总应力σ和有效应力σeff以及孔隙流体压力P之间的关系可以表示为

σ=σeff-α(D)IP

(3)

式中，I为单位张量，二维情况下为[1 1 0]T;α(D)为Biot孔弹性系数，其随岩石损伤演化而变化，即

α(D)=1-KD/Ks

(4)

式中，KD为多孔介质受损后的体积模量，MPa;Ks为骨架颗粒的体积模量，MPa。

将式(3)代入式(2)可得应力平衡方程

∇(σeff-α(D)IP)=0

(5)

式(5)对应的边界条件为

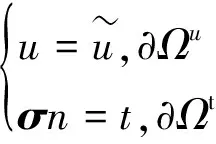
(6)

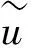
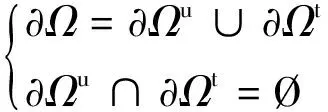
(7)

(2)流体连续性方程：

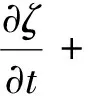
(8)

式中，ζ为流体体积增量，m3;v为流体流速，m3/s。

假设流体流动符合Darcy定律，则流体体积增量和流速可表示为

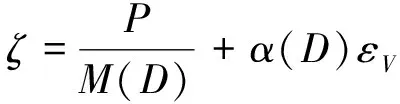
(9)

(10)

式中，M(D)为Biot模量，Pa，如式(11)所示;εV为体积应变;k为各向异性渗透率张量，m2;μ为流体黏度，Pa·s。

M(D)=(Ku-KD)/α(D)2

(11)

其中，Ku为不排水体积模量，即岩石未损伤(原始状态下)的体积模量。将式(9)和(10)代入式(8)，得到多孔弹性介质的流体连续性方程

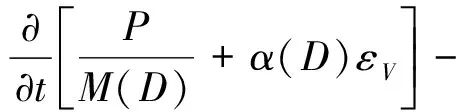
(12)

式(12)对应的边界条件为

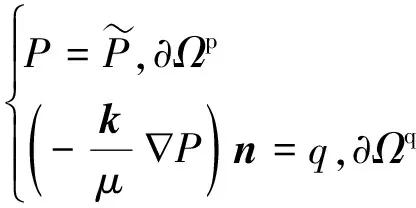
(13)

其中，q为注入排量;∂Ωp为压力场Dirichlet边界;∂Ωq为压力场的Neumann边界。求解域的各边界满足:

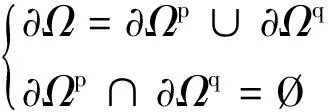
(14)

压裂过程中由于岩石破裂，使得流体沿破裂面切向的流动能力大于沿破裂面法向的流动能力，即地层岩石渗透率为各向异性。因此，对于二维情况，各向异性渗透张量可写为

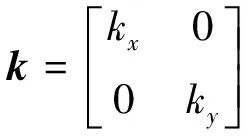
(15)

其中，kx为x方向的渗透率，m2;ky为y方向的渗透率，m2。kx和ky是由岩石的初始渗透率和裂缝渗透率加权组成:

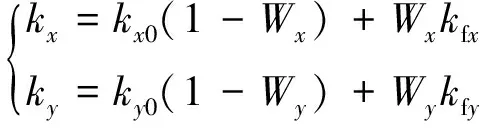
(16)

式中，kx0为岩石基质在x方向的初始渗透率，m2;ky0为岩石基质在y方向的初始渗透率，m2;kfx为x方向的裂缝渗透率，m2;kfy为y方向的裂缝渗透率，m2;Wx为x方向的渗透率加权系数;Wy为y方向的渗透率加权系数。

裂缝渗透率的计算模型为

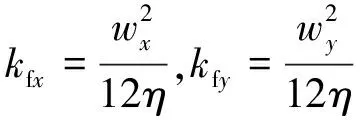
(17)

其中，η为裂缝面形状因子，本文取1;wx,wy为裂缝宽度，本文假设仅当高斯结点处的应变超过临界应变时岩石才会破裂产生裂缝。因此，可以将裂缝宽度的计算公式表示为

(18)

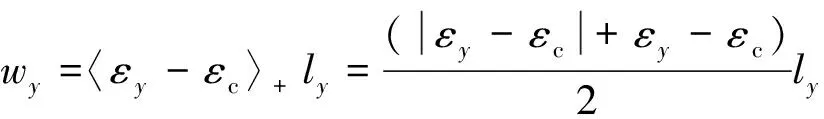
(19)

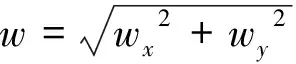
(20)

式中，εx为高斯结点处x方向的应变;εy为高斯结点处y方向的应变;εc为临界应变;lx为x方向的单元长度，m;ly为y方向的单元长度，m。

渗透率加权系数代表水力裂缝对计算单元渗透率的贡献，等于裂缝宽度与单元长度的比值，即

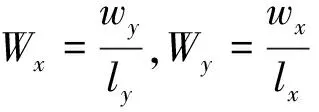
(21)

临界应变与临界拉应力之间关系[30]可表示为

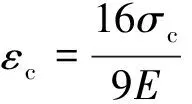
(22)

式中，E为弹性模量。

1.3 数值求解

式(5)应力平衡方程与式(12)流体连续性方程相互耦合，构成了渗流-应力耦合非线性方程组。式(5)和式(12)分别与位移场权函数Wu和压力场权函数Wp相乘，并在计算域上积分，利用散度定理并结合边界条件可得应力平衡方程和流体连续性方程等效积分“弱”形式:

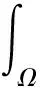
(23)

(24)

其中，C为弹性矩阵，是应力应变转换的关系矩阵。对于每个计算单元的位移场、压力场和对应权函数构造相应的插值函数，其插值形式为

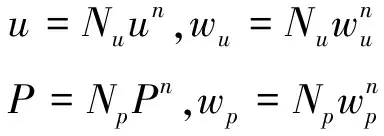
(25)

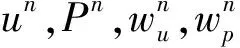
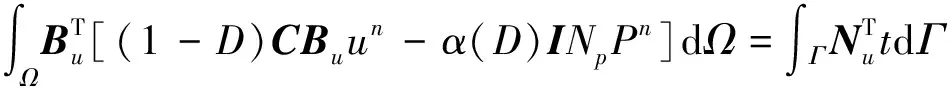
(26)

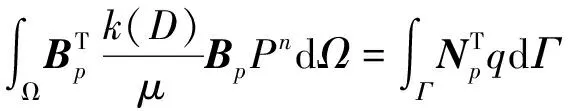
(27)

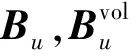
采用向后欧拉法对式(27)中关于时间导数的项进行离散，即

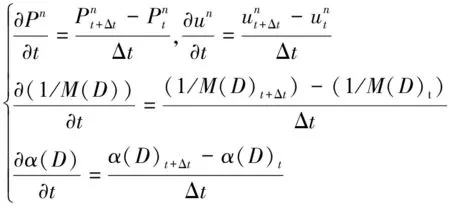
(28)

将式(28)代入式(27)，并将第n+1个时间步变量的下标去掉，则式(27)可写为

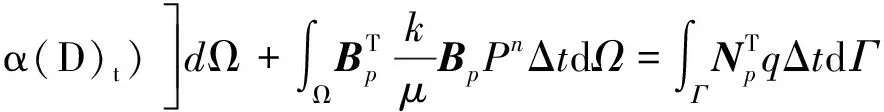
(29)

采用Newton-Raphson迭代法求解渗流-应力耦合方程组，因此将式(26)和(29)写成余量的形式:

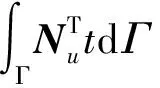
(30)

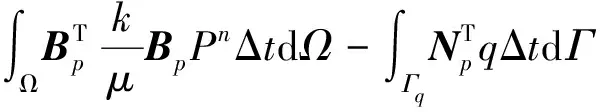
(31)

其中，Ru为位移方程的余量;Rp为压力方程的余量。则渗流-应力耦合方程组在第i个迭代步的Newton-Raphson(NR)迭代格式可写为

(32)

式(32)左边第1项为雅可比矩阵J，各分量为

(33)

通过式(32)可求得第i个迭代步的位移增量δuh和压力增量δPh，进而得到第i+1个迭代步的位移和压力的试探解，即

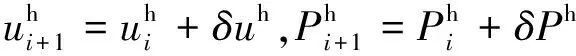
(34)

若位移场和压力场的误差都满足式(35)所示的收敛条件时，迭代结束，否则继续迭代:

‖Ru‖≤tol‖Ru0‖,‖Rp‖≤tol‖Rp0‖

(35)

2 模型稳定性与正确性分析

2.1 模型收敛性与稳定性验证

通过比较3个不同时间步长的模拟结果来验证模型收敛性和稳定性。

如图1所示，计算区域为边长等于16 m的正方形，在计算区域中心有一条沿y方向长度为1.5 m的初始裂缝;固定左边界在x方向上的位移，同时固定下边界在y方向上的位移，并在右边界的x方向上施加12 MPa的压应力，在上边界的y方向上施加16 MPa的压应力。初始孔隙流体压力和沿外边界的流体压力P均设置为5 MPa。计算区域被网格尺寸为0.25 m的有限单元均匀离散。3个不同算例中时间步长分别设置为3.0，4.5，6.0 s。从注入点以恒定的注入速度q=1.5×10-3m2/s注入流体，注入总时间36 s。模拟用到的其他参数见表1。

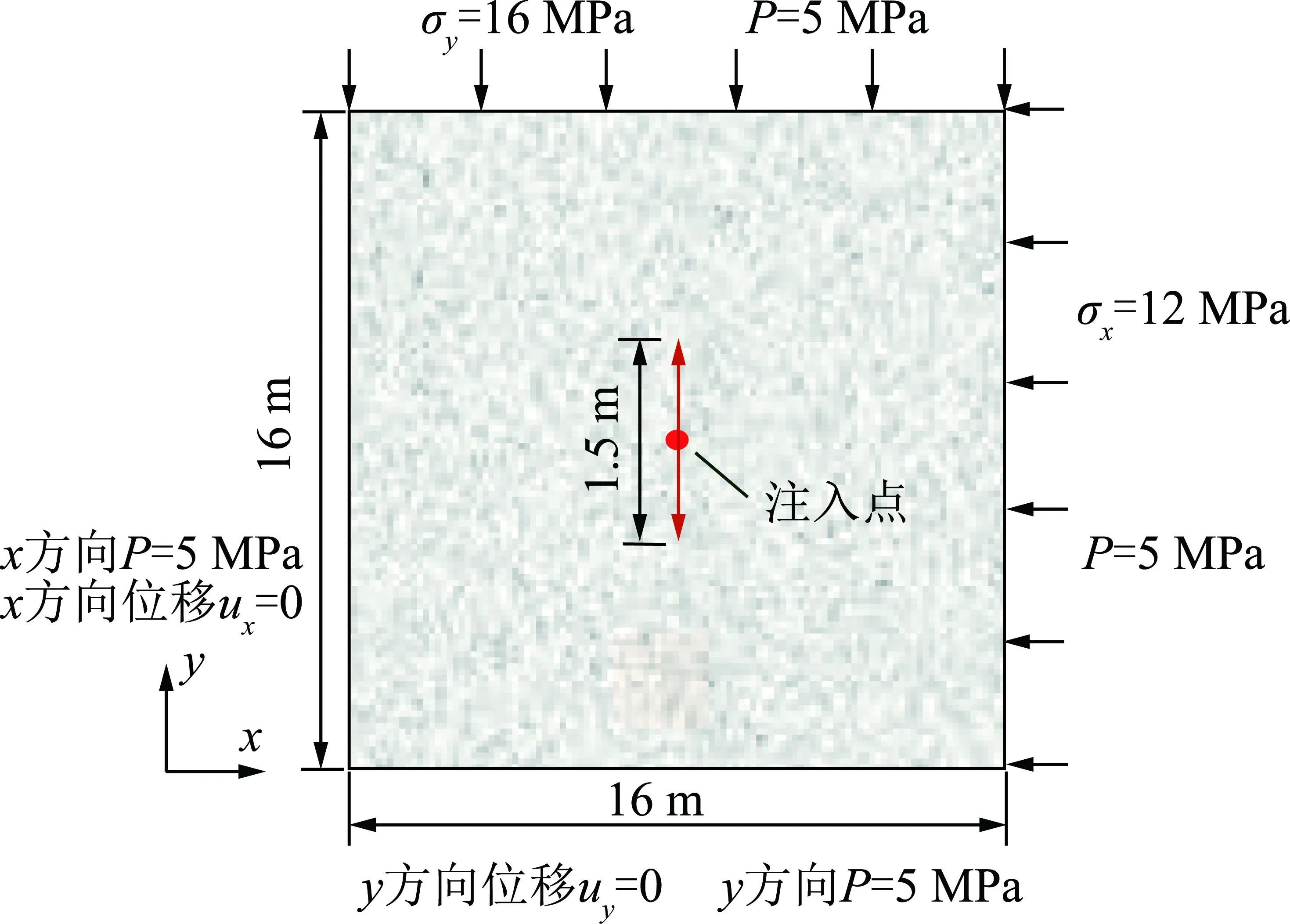
图1 计算区域和边界条件示意Fig.1 Schematic diagram of computational domain and boundary conditions

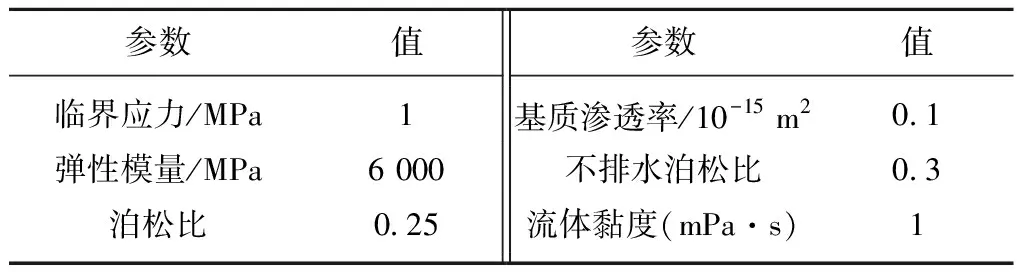
表1 验证模型参数Table 1 Parameters of model verification

在3种不同时间步长情况下，损伤云图、压力云图和裂缝宽度云图几乎相同，裂缝都沿y方向扩展演化(图2～4，其中，D为损伤程度，0表示完好无损，1表示完全失效)。基质渗透率较低，导致由于压裂液滤失而造成压力升高的区域较小。水力裂缝内流体压力几乎相同，即水力裂缝内压降较小。由图5可知，在压裂初始阶段，3种不同时间步长下注入点压力值相差较大，但是当注入时间超过18 s后，不同时间步长下注入点压力值相差较小，并且在注入结束时注入点压力相对误差仅为0.15%，由此验证了该模型的收敛性和稳定性。

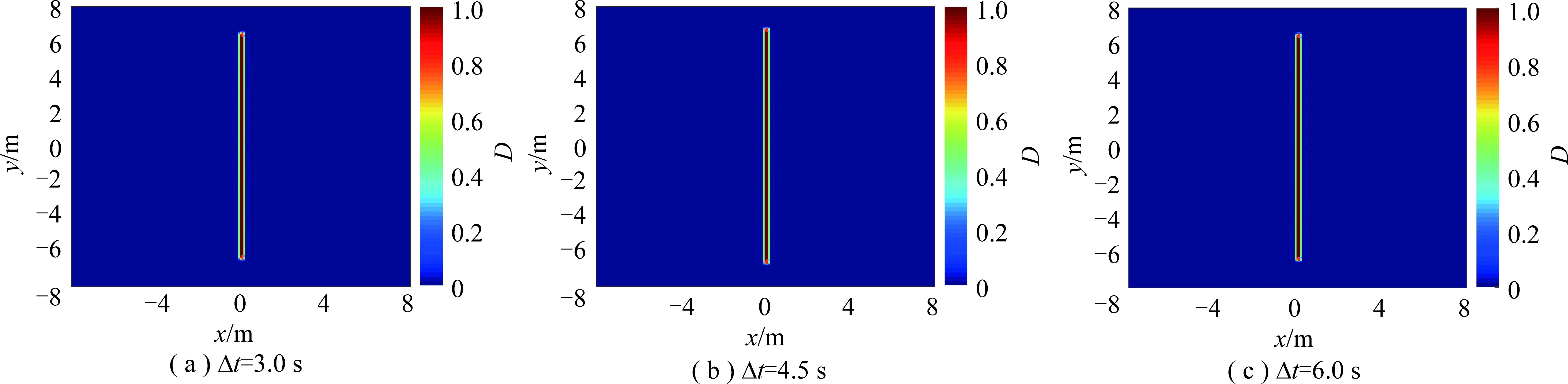
图2 3种不同时间步长情况下注入结束时损伤程度云图Fig.2 Damage distribution contours at the end of injection time in three different time steps

2.2 模型正确性验证

为了验证模型缝宽计算方法的正确性，将上述算例的计算结果与缝宽解析公式计算得到的结果进行对比。由2.1节模拟结果可知，水力裂缝内流体压力几乎相同，而在缝内流体压力均匀分布条件下，裂缝宽度计算公式[31]为

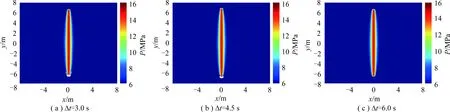
图3 3种不同时间步长情况下注入结束时压力云图Fig.3 Pressure distribution contours at the end of injection time in three different time steps

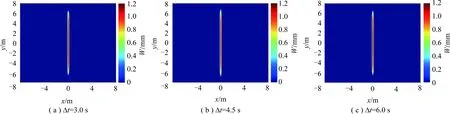
图4 3种不同时间步长情况下注入结束时裂缝宽度云图Fig.4 Fracture width distribution contours at the end of injection time in three different time steps

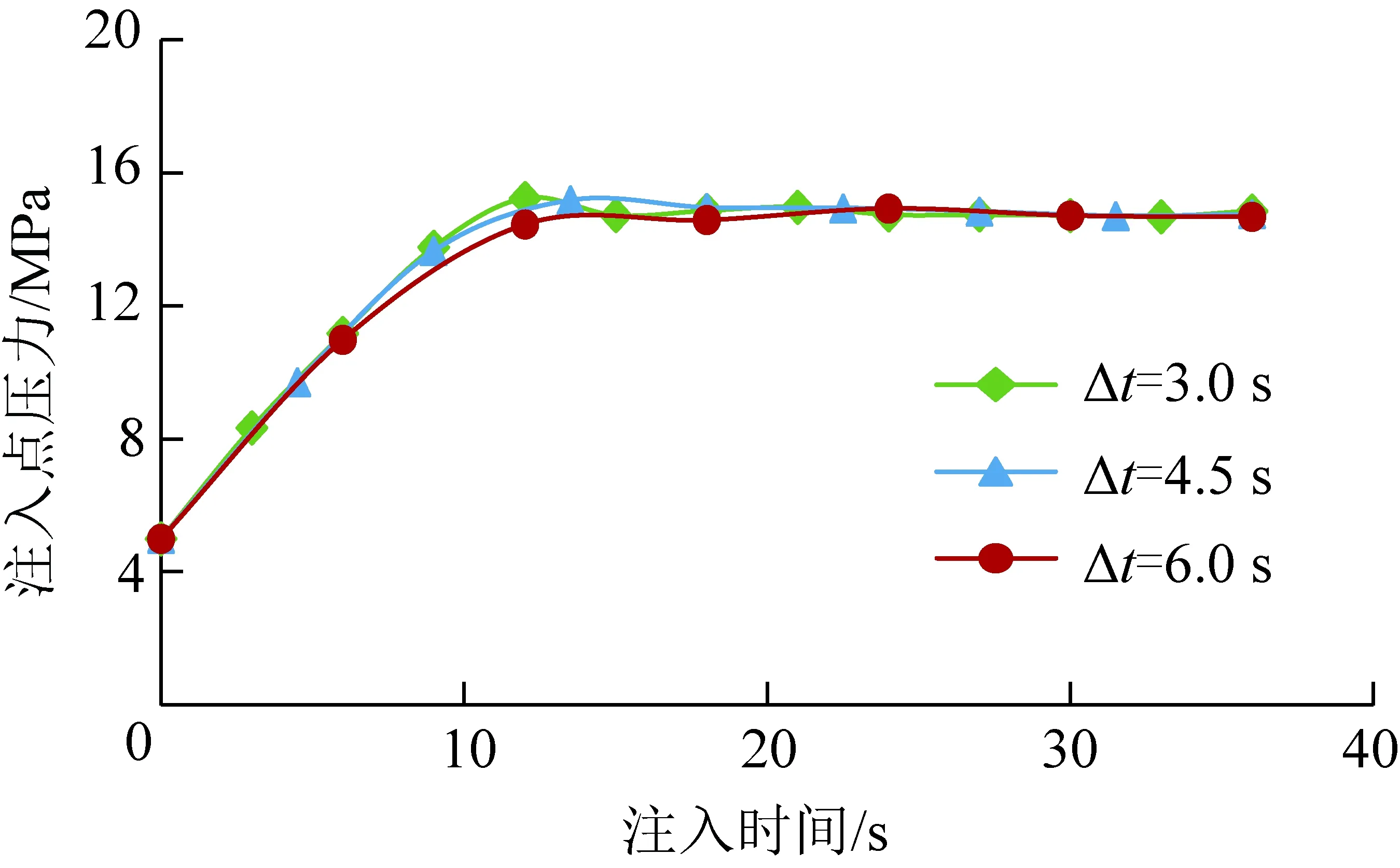
图5 3种不同时间步长情况下注入点压力随时间变化Fig.5 Pressure at the injection point versus injection time in three different time steps cases

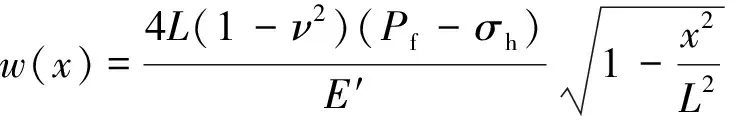
(36)

式中,ν为泊松比；Pf为缝内流体压力，上述算例模型计算结果为12.273 MPa;σh为垂直于裂缝面的远场地应力，在模拟算例中为左边界施加的压应力(12 MPa);L为裂缝长度，算例模型计算得到裂缝半长为5.75 m;x为裂缝面上任意一点到注入点处的距离。

2个不同模型计算得到的裂缝宽度沿缝长方向的分布曲线差异较小，平均误差仅为2.75%(图6)。由此验证了本文模型缝宽计算公式的正确性。

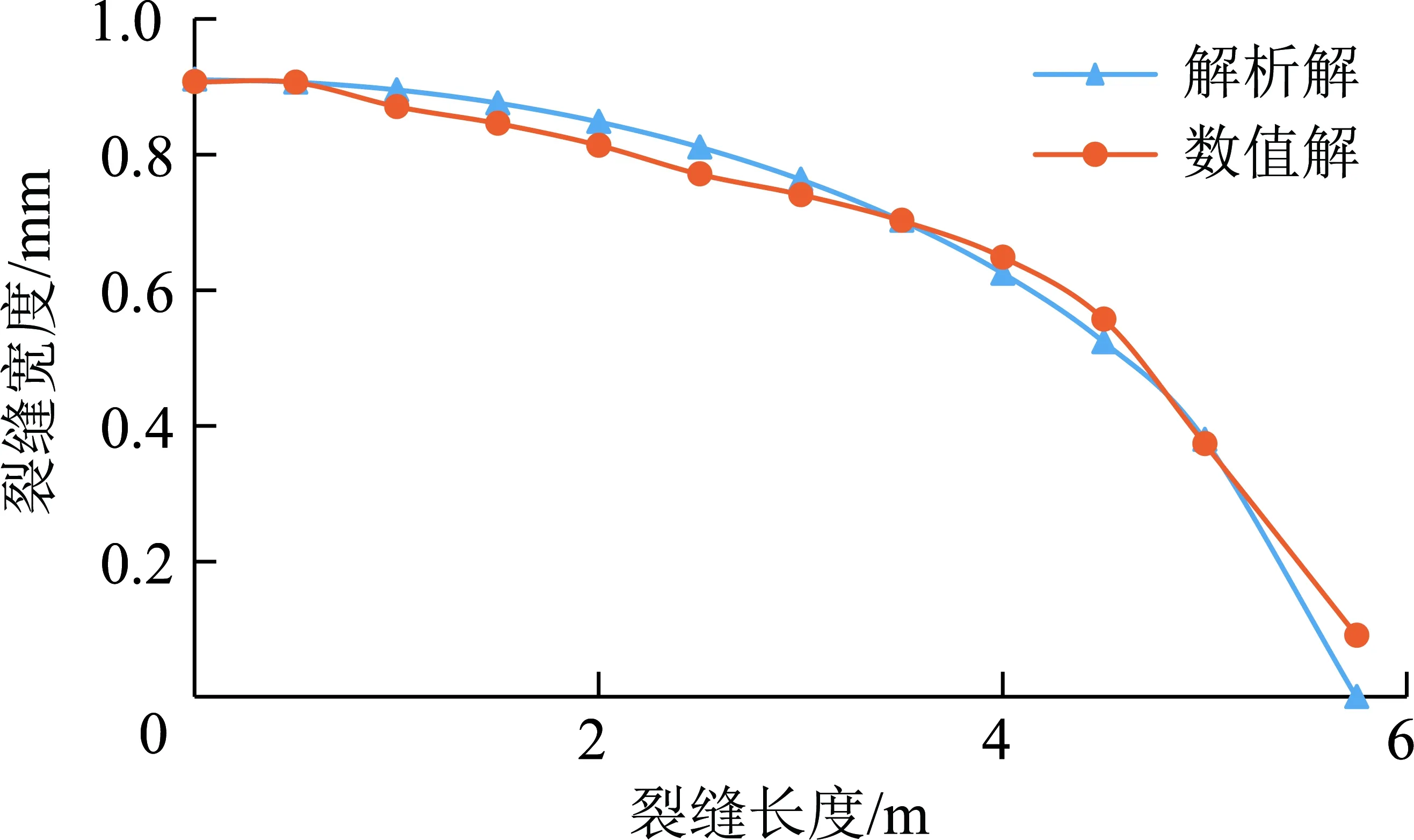
图6 数值模型和解析模型的裂缝宽度对比Fig.6 Fracture width comparison between numerical model and analytical model

3 算例分析

影响多层叠置煤层中水力裂缝纵向扩展的关键因素包括地质因素(原位应力差、界面强度、弹性模量和泊松比)以及工程因素(压裂液黏度)。计算区域和边界条件如图7所示，其中，σhs为砂岩水平地应力，σhc为煤岩水平地应力。模拟用到的其他参数见表2。

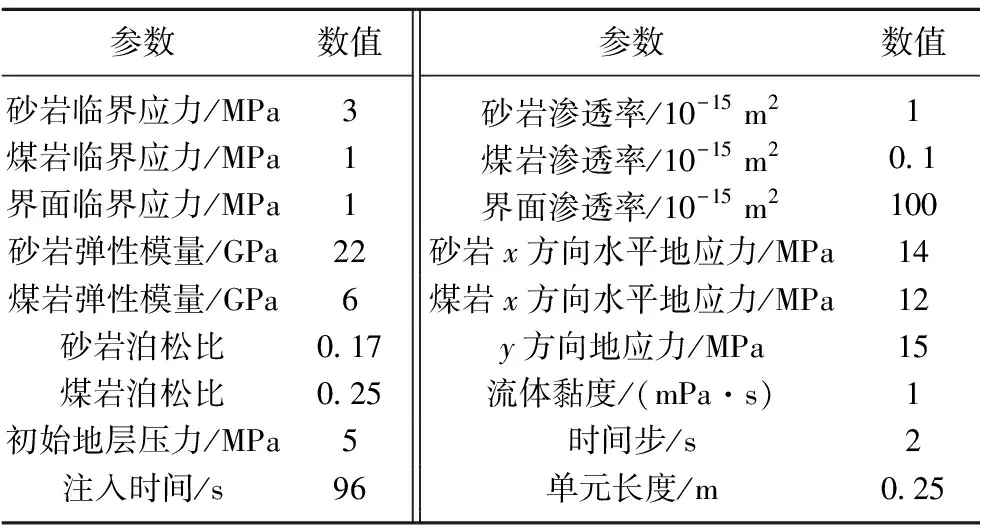
表2 模拟使用的地层参数Table 2 Parameters used in simulation

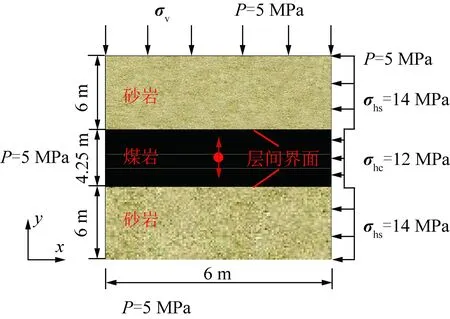
图7 模拟使用的计算域和边界条件示意Fig.7 Schematic diagram of computational domain and boundary conditions used in the simulation example

3.1 原位应力差对裂缝扩展的影响

本节将分析原位应力差即垂直方向(y方向)上的地应力与隔层(砂岩层)中x方向上的水平地应力之差对裂缝纵向延伸的影响。3个算例中注入流体速度q=2.2×10-3m2/s，垂直方向地应力分别为15,16和17 MPa。

分析模拟结果(图8～10)可知，当原地应力差较小时，水力裂缝从煤层扩展至层间界面后转向沿界面扩展，虽然水力裂缝会开启层间界面，但是界面处的裂缝宽度比煤岩层中裂缝宽度小。当原地应力差增大至3 MPa时，水力裂缝直接穿过层间界面而延伸到上下砂岩层，但由于层间界面渗透率比基岩高，因此流体在层间界面处的流动距离大于在基岩中的流动距离。由于损伤程度云图、压力云图和缝宽云图轮廓具有相似性，因此在后续算例中仅给出损伤云图来描述裂缝延伸形态。

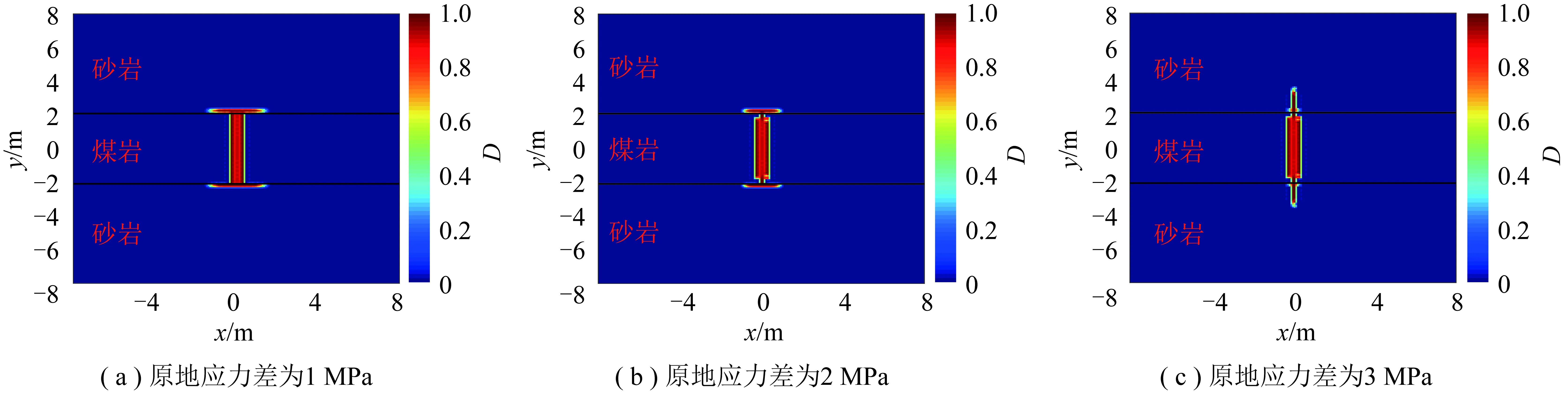
图8 3种不同原地应力差下注入结束时损伤程度云图Fig.8 Damage distribution contours at the end of injection time in three different in-situ stresses difference cases

3.2 界面强度对裂缝扩展的影响

3个算例中，垂直方向上的地应力为17 MPa，注入时间为96 s，模拟界面强度分别为0.50，0.75，1.00 MPa时的裂缝纵向扩展情况(图11)。

由图11可知，界面强度越大，水力裂缝越可能穿过界面而延伸到上下砂岩层。分析注入点压力变化曲线(图12(a))，穿过层间算例中注入点压力比沿层间界面延伸算例注入点压力低，而沿层间界面延伸时，层间界面强度越小，注入点压力越小。

3.3 杨氏模量和泊松比对裂缝扩展的影响

算例中，垂直方向地应力为17 MPa，模拟砂岩层中的弹性模量分别为22，16和10 GPa。由于岩石的泊松比通常与弹性模量成反比，故砂岩泊松比分别为0.17，0.20和0.23。

如图13所示，砂岩层弹性模量越大，裂缝高度越大，即较小的砂岩层(盖层)弹性模量会降低裂缝高度。分析压力变化曲线(图12(b))，砂岩层弹性模量越大，裂缝穿层后注入点压力越高。

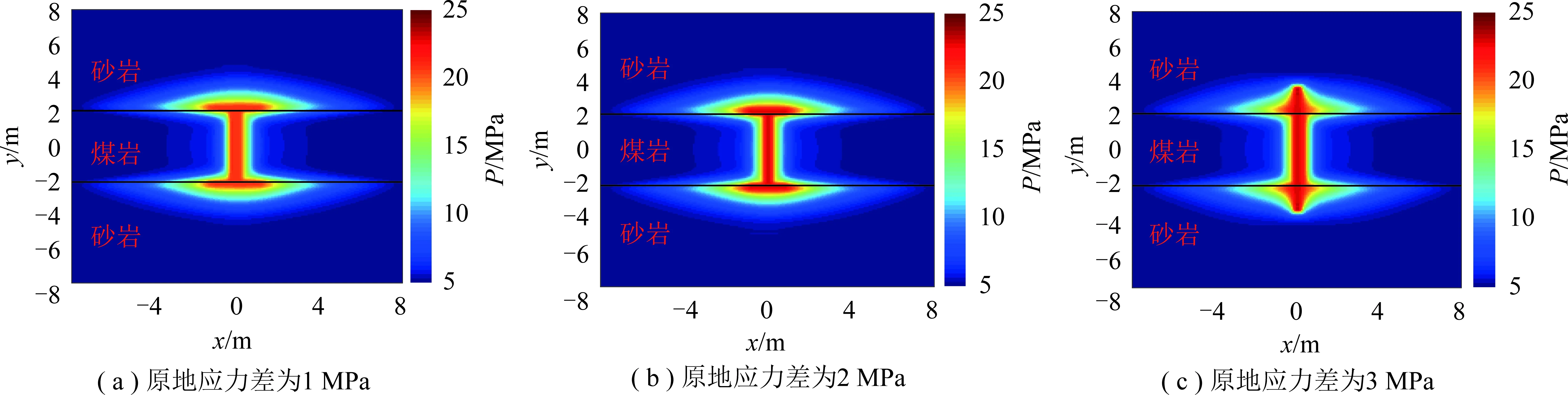
图9 3种不同原地应力差下注入结束时压力云图Fig.9 Pressure distribution contours at the end of injection time in three different in-situ stresses difference cases

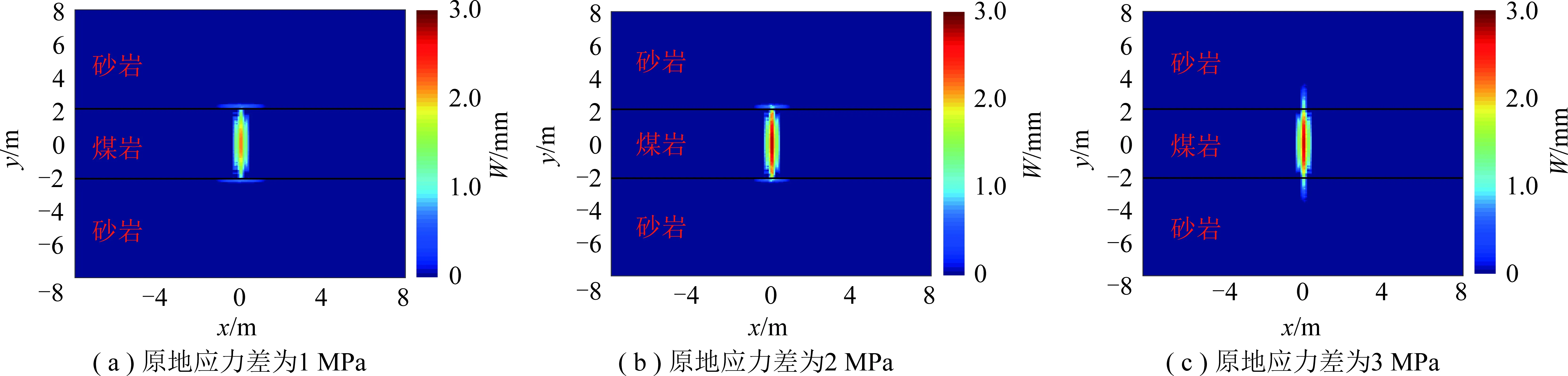
图10 3种不同原地应力差下注入结束时裂缝宽度云图Fig.10 Fracture width distribution contours at the end of injection time in three different in-situ stresses difference cases

图11 3种不同界面强度下注入结束时损伤程度云图Fig.11 Damage distribution contours at the end of injection time in three different interface strength cases

3.4 压裂液黏度对裂缝扩展的影响

算例中，垂直方向地应力设为17 MPa，模拟压裂液黏度分别为0.1，0.5，1.0 mPa·s时的裂缝纵向扩展情况(图14)。

结果显示，压裂液黏度越大，水力裂缝越有可能穿过界面延伸到上下砂岩层，且黏度越大，穿层后裂缝高度越大;压裂液黏度的增加，注入点压力随之增大(图12(c))。

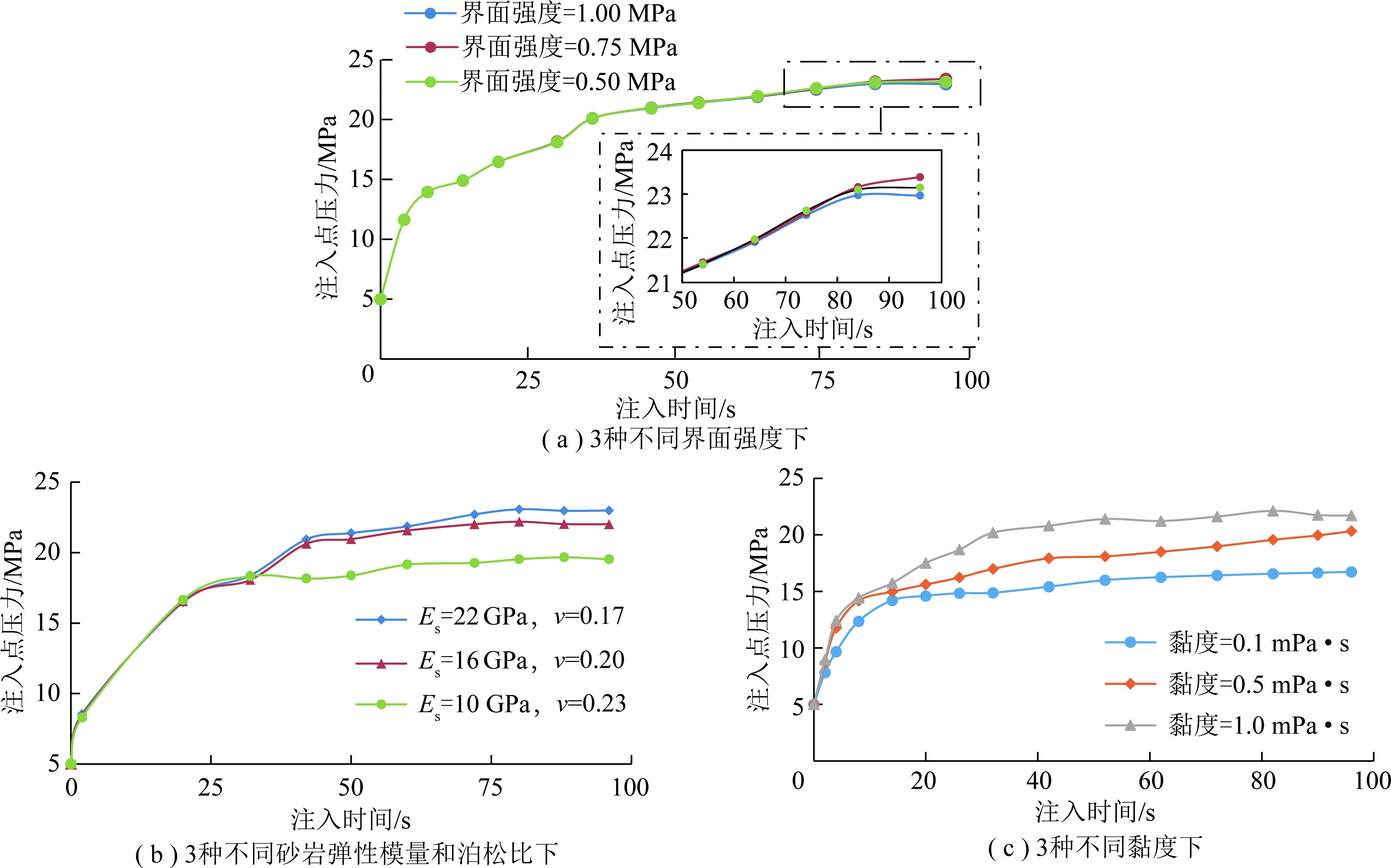
图12 注入点压力变化Fig.12 Pressure at the injection point versus injection time

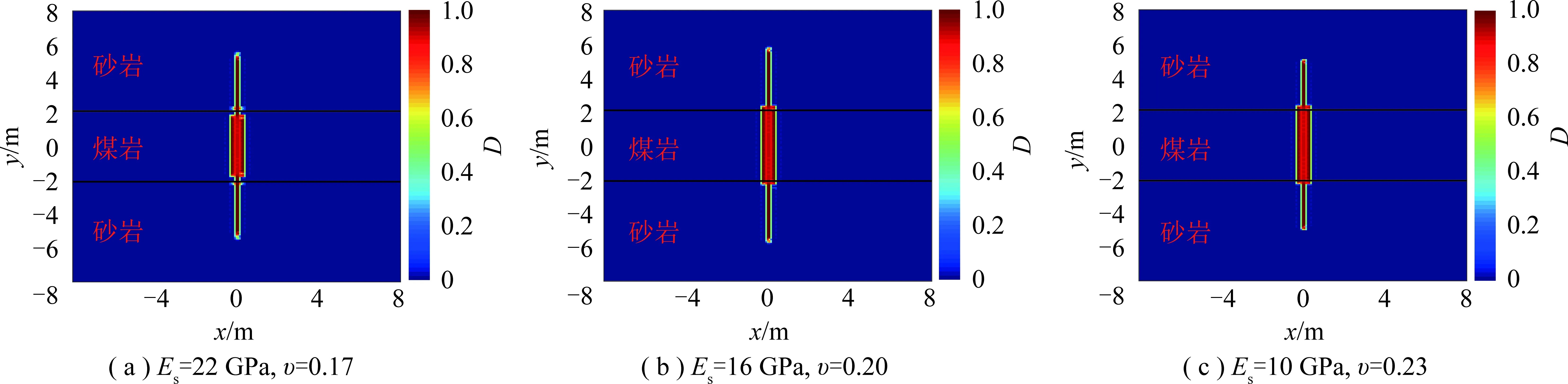
图13 3种不同砂岩弹性模量和泊松比下注入结束时损伤程度云图Fig.13 Damage distribution contours at the end of injection time in three different young modulus and poisson ratio of sandstone cases

4 结 论

(1)较高的原地应力差、界面强度将使水力裂缝穿过界面并在砂岩层中扩展;砂岩层弹性模量越大裂缝穿层后高度越大。

(2)压裂液黏度越大，压裂裂缝越容易穿过层间界面延伸到上下隔层，且黏度越大，穿层后裂缝高度越大。

(3)虽然在某些情况下水力裂缝会打开砂煤岩界面，但界面处的裂缝宽度比煤岩中的裂缝宽度小得多。

(4)水力裂缝沿层间界面转向延伸的缝内流体压力高于直接穿过界面延伸到上下隔层的缝内流体压力。