基于路径积分的叠后绕射波偏移成像

李 勤，沈鸿雁，王 鑫，赵 静，李 萌

(1.西安石油大学 地球科学与工程学院，陕西 西安 710065；2.陕西省油气成藏地质学重点实验室，陕西 西安 710065)

煤田地球物理勘探的任务之一是准确识别和追踪断层、陷落柱、富水层等异质体(区)，以避免(或减轻)开采过程中的地质灾害[1-9]。地震绕射波由于具有较高的分辨力和与小尺度异质体的准确对应关系，近年来备受勘探人员重视。其实，早在20世纪50年代，KREY[10]等就已经发现来自断块、尖灭等处的绕射波，之后TROREY[11],BERRYHILL[12]和Klem-Musatov[13]等对其进行了研究并建立了基本的绕射波理论体系。随着研究的不断深入，人们发现除了能有效检测异质体的存在，绕射波还可用于描述异质体的方位及边界等特征[14]，充分利用绕射波对地下异质体(区)的精细勘探具有十分重要的意义[15-18]。

绕射波利用的关键是对其进行准确成像，但独立的时差规律使得它在与反射波同时成像时不仅得不到正确收敛，而且还会因能量较弱而被掩盖。此外，绕射成像对速度扰动较为“敏感”[19]，很小的速度变化都可能使其离开最佳的收敛状态，因此偏移时需要提供精确的速度模型，这也导致了绕射成像实现起来比较困难。虽然近年发展出许多专门针对绕射波的成像方法和技术，也取得了一定的成像效果[20-25]，但大多还是对速度模型有着较强的依赖[26]。

路径积分法是一种较新的地震成像技术，因无需预先构建成像速度模型就可实现成像，所以引起了研究者的极大关注[27-30]。目前，该方法在直接成像中的应用基于称为“速度延拓”的偏移算法。CLAERBOUT[31]提出了速度延拓偏微分方程，将其应用于速度分析；FOMEL[32-33]指出在各向同性情况下，零偏移距速度延拓是一个连续和解析的过程，并给出了方程的f-k域解；BURNETT等[34]认为路径积分和速度延拓的结合拓展出一种不依赖速度模型的成像方法；LANDA等[35]由共成像点道集的平面度计算了权值，说明加权因子的引入可增强路径积分成像的协调性；MERZLIKIN等[36]进行了路径积分法绕射波成像，并且推导了偏移滤波器的解析形式。上述研究验证了路径积分成像的可行性，探索了其在地震勘探中的应用潜力。

笔者在已有理论的基础上，研究针对叠后绕射波的f-k域路径积分成像方法，以进一步改善绕射波的成像质量，提高破碎带、岩溶、采空区等小尺度异质体(区)的探测精度。

1 方法原理

1.1 路径积分速度延拓

速度延拓(Velocity Continuation，VC)是一种以速度为传播变量的波形过程[33]，描述了时间偏移同相轴在不同速度下的形态变化。零偏移距各向同性时，该过程可表示为一个线性双曲形式的偏微分方程[31,33,36]：

(1)

式中，P(x,t,v)为地震波场，x，t，v分别为空间坐标、单程走时和半偏移速度。

当v=C时(C为非负常数)，求解式(1)的过程称为等速延拓，解得的P(x,t,C)即该速度下的恒速时间偏移剖面。一般可引入变量τ来替换单程走时t(τ=t2)，通过对时间轴的“拉伸”(重采样)处理将方程简化为傅里叶域中的常微分方程并得到其解析解：

(2)

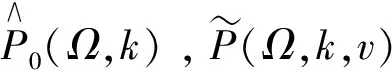
基于速度延拓的连续性以及绕射同相轴顶点在该延拓过程中的“平稳性”，可利用连续叠加等速延拓剖面的方式来实现绕射波成像[37-39]，继而得到基于路径积分的速度延拓偏移滤波器：

(3)

其中，FPI(Ω,k,va,vb)为f-k域路径积分偏移滤波器，其性能取决于Ω，k以及速度积分限va和vb。通过式(3)得到的成像结果可认为是由给定区间内的所有等速延拓剖面等权重叠加而成。

为了进一步增加成像的协调性，提高成像质量，可在上述滤波器中加入高斯因子：

(4)

滤波器的解析表达式(式(4)第2个等号)基于复指数积分函数与虚误差函数成正比的性质得出，通过求取虚误差函数端点值的方式，就可快速求出相应的偏移滤波器。滤波结果经二维逆傅里叶变换后，可进一步输出为成像剖面。与叠后t-x域的偏移不同，f-k域路径积分法主要利用滤波运算进行幅值和相位控制，通过增强绕射波场中的水平(近水平)分量、弱化具有一定倾角的绕射弧侧翼来实现绕射波的偏移成像。

1.2 成像流程

f-k域路径积分法叠后绕射波偏移成像流程如图1所示，具体实施步骤：

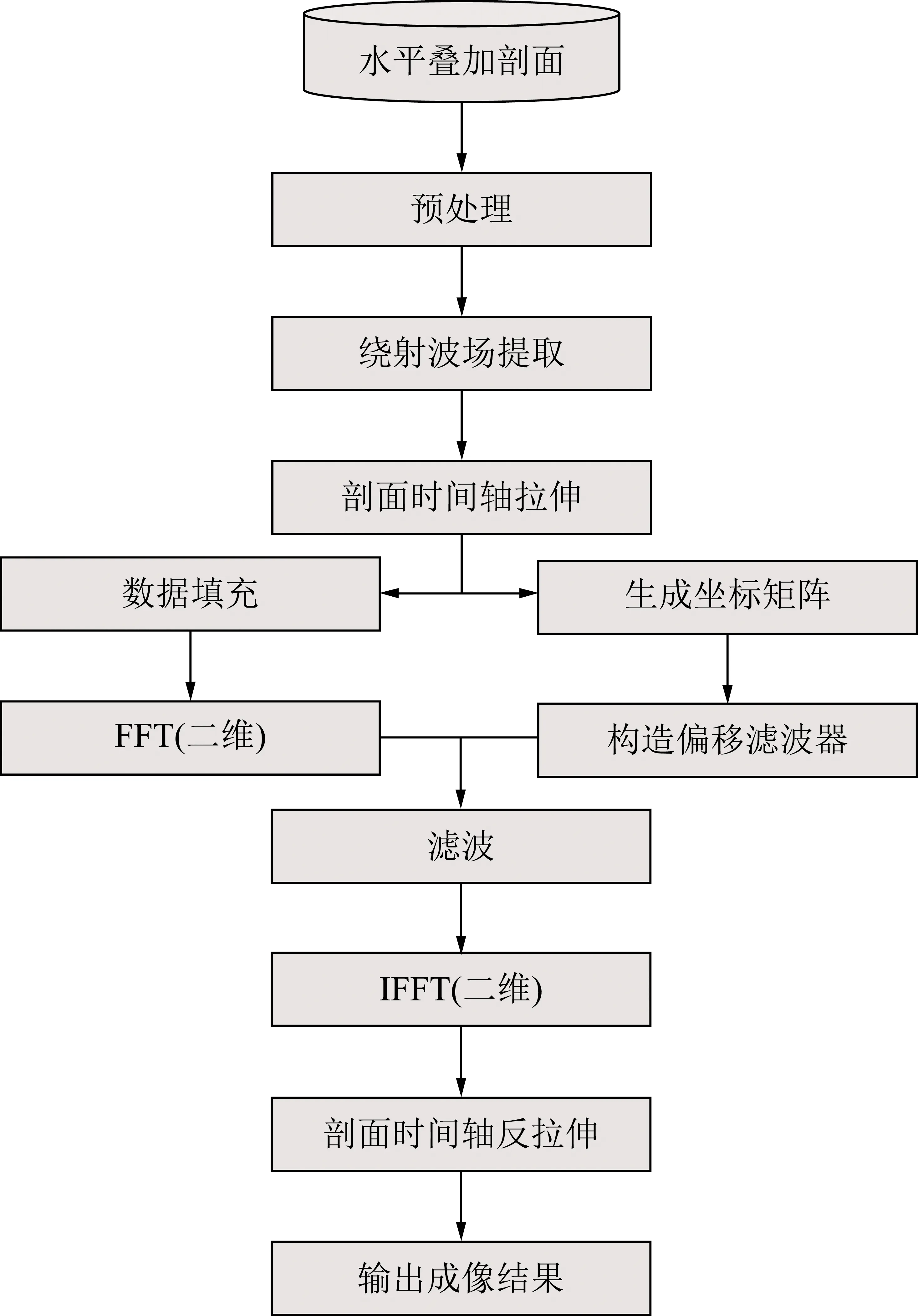
图1 路径积分法成像流程Fig.1 Flowchart of path integral method

(1)输入原始地震记录(水平叠加剖面)，对其进行预处理(能量补偿、干扰波压制等)，然后选择合适的波场分离方法提取绕射波场Dx×y(x行y列)。可选用SVD(Singular Value Decomposition)法提取绕射波[40-44]，基于水平叠加剖面中反射波和绕射波横向相干性和连续性方面的明显差异，通过SVD带通滤波实现2者的分离。

(3)按照拉伸填充后的时空域剖面的网格参数生成坐标矩阵Ωm×1和k1×n，再选取积分限va和vb，由式(4)构造路径积分偏移滤波器Fm×n(复矩阵)。

2 模型数据处理与分析

2.1 单点绕射模型

(1)模型构建。建立了一个单绕射点地质模型来检验方法的正确性(图2(a))。如图2(a)所示，速度为1 500 m/s的均匀地层中，存在1个半径为15 m的球形异质体，球心距地表375 m，其速度为4 500 m/s。采用有限差分解波动方程的方法进行正演模拟，自激自收观测系统，震源子波为Ricker子波，主频为40 Hz，道距为2 m，道数为1 000道，采样率为1 ms，采样点数为1 000点。

正演获得的地震剖面如图2(b)所示，该剖面可等效为水平叠加剖面。从该地震剖面可看出，异质体引起的地震响应为一条具有双曲线特征的绕射波同相轴，顶点在500 ms处，跨度约2 km，能量随着远离绕射源呈现出衰减特性。为了贴近实际情况，在地震剖面中加入了随机噪声(图2(c))，其信噪比约为10∶1。

图2 单点绕射模型及地震剖面Fig.2 Single-point diffraction model and seismic section

(2)等速延拓成像。由于路径积分速度延拓成像基于等速延拓原理，因此需要先检验等速延拓的有效性。根据偏移流程，首先对原始数据(图2(c))进行时间轴拉伸处理，获得地震剖面如图2(d)所示。在拉伸后的剖面中，绕射同相轴顶点“上移”，其附近变得“平缓”，侧翼则更加“陡峭”。

根据式(2)，在3个不同的速度下对拉伸剖面(图2(d))进行了等速延拓实验，成像结果在还原时间轴后如图3所示。当延拓速度vvc远小于最佳成像速度v0时，绕射同相轴两翼变短内收(图3(a))；vvc接近v0时，收敛于顶点(图3(b))；随着vvc的继续增大，绕射弧朝反向重新展开(图3(c))。延拓速度的连续变化使绕射同相轴两翼持续产生相移，而在该过程中，其顶点位置保持静止。

图3 不同速度下的等速延拓结果比较Fig.3 Comparison of constant velocity continuation results with different imaging velocities

上述实验说明等速延拓可有效进行绕射波偏移，其成像的关键在于延拓速度的选取。只有在最佳成像速度附近进行延拓才能使绕射波准确成像，否则将导致其欠偏移(速度太小)或过偏移(速度太大)。值得注意的是，对于等速延拓而言，最佳的延拓速度并非精确对应于真实速度，原因或与剖面时间轴拉伸有关。

(3)路径积分速度延拓成像。早先的速度延拓成像是通过一系列离散的速度进行等速延拓，然后优选高聚焦量的部分拼接形成最终的成像剖面。这种做法不仅运算成本高，而且成像质量还会受速度离散化程度的影响，路径积分为该问题的解决创造了条件，通过积分解可实现速度区间内等速延拓剖面的连续叠加。

通过式(3)构造的路径积分偏移滤波器以及相应的成像结果如图4所示，速度区间取700～2 500 m/s。图4(a)，(b)分别为其对应的f-k幅值谱、相位谱，滤波器幅值谱中的黑色区域称为“主瓣”，两侧伴有若干条浅灰色细长“旁瓣”，它们关于k=0对称，且波数宽度随着频率的升高呈非线性增加；图4(c)为绕射波成像剖面，经过偏移后绕射弧顶点附近的同相轴能量得到了显著增强，侧翼也得到一定程度的压制，但其对侧却出现了一条与之共享绕射顶点的“反向弧”，它们形成的“X”状同相轴对应4条未完全收敛的“尾线”；图4(d)给出了相应的幅值谱响应(Ω=375 Hz)，主、旁瓣光滑可辨，其幅度和波数宽度随着远离零波数轴衰减强烈；图4(e)为滤波器相位谱响应，其值从k=0时的零相位向两侧逐渐减小到 -π/2，并且在|k|持续增大的过程中发生若干次正负“跳跃”，整体呈“锯齿”状，换言之，主瓣区相位稳定，而旁瓣的相位变化则比较剧烈。

图4 路径积分滤波器和绕射波成像结果Fig.4 Path integral filter and diffraction imaging result

图4(c)中的“反向弧”(或称为尾线)是路径积分法固有的偏移“剩余”，它与滤波器旁瓣的存在密切相关。图4(f)为地震剖面滤波前后的幅值谱响应(Ω=375 Hz)，相较于原始曲线(灰色线)，滤波后曲线的幅值(黑色线)在零波数附近有一个明显的增强，远离k=0处则被大幅削弱。然而，由于旁瓣(特别是图4(d)中箭头处的“第1旁瓣”)的“泄漏”效应，导致曲线主峰两侧出现了明显的“旁峰”(图4(f)中箭头所指)，这些旁峰在变换回t-x域时，可能共同产生了偏移剖面中的尾线。从叠加角度来说，给定速度范围的开区间内，绕射双曲线的侧翼在连续等速延拓偏移求和的过程中相互抵消，而区间端点处的偏移却因无法抵消而被保留，从而导致成像剖面中产生2条对应积分上、下限的同相轴。

(4)加权路径积分速度延拓成像。在积分区间较大的情况下，经过路径积分法(式(3))偏移的绕射弧顶点和尾线存在较大的幅值差异(图4(f))，因此后者产生的影响基本可以忽略；但区间较小时，尾线可能与其他同相轴发生相长干涉而产生虚假特征，需要采取一定的措施来压制这类干扰。为此，构造了高斯加权路径积分偏移滤波器(式(4))来削弱尾线的影响。取速度为700～2 500 m/s,vbias=1 600 m/s，σ=200 m/s，构建的滤波器f-k幅值谱、相位谱及相应谱的响应(Ω=375 Hz)分别如图5(a)，(b)，(d)，(e)所示。与未加权的滤波器(图4(a)，(b)，(d)，(e))相比较，高斯加权有效压制了滤波器的幅值谱旁瓣，并使其相位在远离零波数轴的区域“失稳”，降低了大倾角分量贡献的“稳定叠加”。图5(c)为高斯加权路径积分法绕射波成像剖面，不仅有效弱化了尾线，还使绕射点得到了进一步的聚焦。从滤波前、后剖面的幅值谱响应(Ω=375 Hz)(图5(f))也可看出，两侧的幅值被削弱，而中间的小波数区域得到了保留。此外，在原始绕射剖面中加入的随机噪声，偏移后表现为细微的水平同相轴，对成像结果并无明显影响，说明该方法具有一定的抗噪能力。

图5 高斯加权路径积分滤波器和绕射波成像结果Fig.5 Gaussian weighted path integral filter and diffraction imaging result

(5)成像参数控制。高斯加权路径积分法成像的质量受控于积分区间[va,vb]、速度偏量vbias和标准差σ等参数。为此，基于单点绕射模型就成像参数的优选开展了实验研究。

无论加权与否，路径积分法的成像效果均受滤波器主瓣区的控制。理论上，增大积分范围(速度区间)会减小主瓣的波数宽度，使其变窄，这意味着成像剖面中对应区间端点的欠、过偏同相轴的形态将发生改变；同时，适当增大速度区间还可以提高主瓣幅值，进而凸显绕射顶点。然而，过大增加积分范围将以牺牲运算成本为代价。

当σ限定时，最佳成像速度与积分区间[va,vb]的包含关系将直接影响成像效果，区间整体低于或高于最佳速度时均无法正确成像。此外，积分下限越远离最佳速度，成像剖面中绕射点两侧的同相轴欠偏越严重(图6(a))；反之，则会导致严重过偏(图6(c))。获得良好成像结果的前提是必须使积分区间包含最佳成像速度(图6(b))，此时尾线的长短受积分上、下限影响，而绕射点的幅值强弱则与速度区间的大小有关。

图6 不同积分限的路径积分成像结果比较Fig.6 Comparison of path integral imaging results with different velocity ranges

一般而言，对于确定的地震剖面，其成像速度往往分布于一个较大的区间内，但受目标层的限制，必然存在一个更小的、分布更集中的子区间，可将这个含有主要成像速度的区间称为“优势速度区间”。速度偏量vbias指定了优势速度区间所处的位置，在以该速度为中心的邻域内，贡献叠加的权值将被增强。在缺乏先验信息的情况下，vbias可取为积分区间的中点，认为优势速度区间分布在以该点为中心的一定范围内。

在进行高斯加权路径积分法成像时，标准差σ

规定了优势速度区间内贡献的增强程度。由图7可看出，在积分限va,vb和速度偏量vbias限定的情况下，标准差σ越小，vbias附近贡献的权值就越高，绕射收敛越集中(图7(b))，但太小的σ值则容易放大错误速度引起的贡献，使尾线干扰明显增强(图7(c))；当σ值越大时，剖面则越趋向于未加权路径积分法的成像结果(图7(a))。因此，适当选择σ值可有效提高绕射点的分辨率。

图7 不同标准差σ的路径积分成像结果比较(va=1 000 m/s，vb=2 200 m/s,vbias=1 600 m/s)Fig.7 Comparison of path integral imaging results with different standard deviation σ(va=1 000 m/s，vb=2 200 m/s,vbias=1 600 m/s)

当路径积分法应用于实际时，可先大致选取一个合理的速度范围进行偏移，良好的成像剖面应具有均衡的欠、过偏成分，若存在明显的欠偏同相轴，则需要提高积分下限va，而大范围的过偏弧则说明积分上限vb过高。通过不断调整积分限，就可获得一个既包含主要成像速度、又能较好地突出绕射点的速度区间，然后以此为基础确定速度偏量vbias和标准差σ，最后再利用高斯加权路径积分法实现绕射波成像。

2.2 多点绕射模型

为了进一步检验对多绕射点剖面的成像效果，建立了一个含有5个绕射源(标识为a，b，c，d，e)的地质模型(图8(a))，其中均匀地层的速度为3 000 m/s，异质体速度为4 500 m/s，半径为8 m，采用与单绕射点模型相同的模拟方法和数据采集参数获得如图8(b)所示的地震记录(剖面中加入了随机噪声，SNR=10)，利用路径积分速度延拓对该剖面进行偏移成像，取va=1 500 m/s,vb=4 600 m/s，vbias=3 050 m/s、σ=200 m/s。从成像结果来看(图8(c))，5个异质体均得到了准确成像，说明该方法适用于多绕射源成像。

图8 多点绕射模型成像Fig.8 Seismic imaging of multi-point diffraction model

3 实际资料处理与分析

实际地震资料的原始水平叠加剖面如图9(a)所示，该剖面构造较复杂，0～0.5 km存在一个尖灭，由此形成多条绕射波同相轴；在整条剖面(100～300 ms)中存在一套不整合面，由于剥蚀程度的差异，导致地震剖面上也存在数条绕射同相轴，能量较弱，几乎淹没于反射波之下；在剖面的右侧，存在一组空间分布较宽(1.2～1.6 km)、深度跨度较长(100～800 ms)的绕射波，仅靠水平叠加剖面还难以判断该绕射源的形态。反射波叠后偏移成像剖面(图9(b))中绕射波得到了有效收敛，尤其是右侧的绕射波组收敛成一条近乎连续的波阻抗界面，结合该界面两侧错断的同相轴可初步判断该处发育一条较大型的逆断层，但受强反射能量的影响，尖灭点、断点、不整合面的凸点等信息几乎被掩盖在反射同相轴之下，纵、横向分辨率较低。

为了更好地揭示异质体(区)的特征，提取了地震资料中的绕射波场(图10(a))，并分别采用Kirchhoff法和路径积分法对其进行叠后偏移成像处理。与叠后Kirchhoff偏移成像结果(图10(b))相比较，路径积分法成像剖面(图10(c))中，破碎带、风化壳等异质区引起的绕射波得到了有效收敛，清晰地刻画出构造细节，且纵、横向分辨率以及风化壳界面波的连续性均优于叠后Kirchhoff偏移剖面。基于紊乱的地震响应特征，可在剖面中圈划出2个地质异质区：300 ms以浅，清晰展示了由风化壳引起的尖灭点、凸点信息；剖面右侧则揭示出断层及断层引起的破碎异质区，而相关信息在反射波叠后偏移成像剖面(图9(b))中则几乎看不到。

图9 实际资料全波场成像Fig.9 Full wave field imaging of real seismic data sets

4 结 论

(1)f-k域路径积分法是滤波形式的叠加类成像方法，可在给定区间内自动累积稳定贡献，无需预先提供成像速度模型，减少了速度建模时的主观影响，具有流程简单、精度高、稳定性好、运算效率高等优点。

(2)以叠后绕射剖面作为f-k域路径积分法的输入时，强反射波场对成像结果的影响较大，因此在提取绕射波时应尽量保证其干净和完整。

(3)高斯加权路径积分法受控于积分区间[va,vb]、速度偏量vbias和标准差σ等参数，需恰当选择以确保绕射波的成像质量。