让数学原理寓于数学活动之中——《商不变的性质》教学设计及反思

■冯胜 邵承民

让数学原理寓于数学活动之中
——《商不变的性质》教学设计及反思

■冯胜 邵承民

《商不变的性质》是人教版课标教材小学数学四年级上册第93页的教学内容，是学生在知道积的变化规律、学习除数是两位数的除法后，通过计算、观察、比较、抽象以及概括等活动发现、归纳商不变的性质。这部分内容的教学不仅可以巩固所学的计算知识，培养学生初步的抽象、概括能力以及探究能力，同时还能为学生以后学习小数除法以及函数知识做准备。

本堂教学设计，通过将数学原理寄于数学活动之中，让学生经历自主探究的过程，促进和深化了学生对数学思想方法的理解，帮助学生构建了“商不变的性质”这一数学知识，是一个较为有效的课堂教学。

【教学设计】

教学内容：人教版课标教材小学数学四年级上册第93页

教学目标：

1．让学生经历发现、抽象、概括商不变的性质过程，理解并会用这一性质解决有关问题。

2．在发现、归纳商不变的性质过程中，培养学生观察、比较、抽象和概括的能力。

3．培养学生积极思考、勇于探索的学习习惯，感悟“形变值不变”的辨证唯物主义观点。

教学重点：使学生理解商不变的性质，并能用这一性质解决有关问题。

教学难点：使学生发现并归纳概括商不变的性质。

教学关键：引导学生发现算式之间的变化规律，用数学语言进行较为准确的归纳、概括。

教学过程：

一、创设情境，导入新课

1．多媒体课件出示“猴王分桃”的场景，猴王说：“给你6个桃子,平均分给你们3只小猴吧。”小猴一想，连连摇头说:“太少了，太少了。”猴王又说：“好吧,给你60个桃子,平均分给30只小猴，怎么样?”小猴子得寸进尺,挠挠头皮,试探地说:“大王，再多给点行不行啊？”猴王一拍桌子,显示出慷慨大度的样子:“那好吧,给你600个桃子,平均分给300只小猴,你总该满意了吧。”小猴子觉得自己占了大便宜开心地笑了,猴王也笑了。

2．提出问题：你觉得谁是聪明的一笑？为什么？

3．学生自由回答：猴王的笑是聪明的一笑，按照这三种分法，每只小猴得到的都是2个桃子。

4．教师启发思考：你是怎样知道每次分的一样多的呢？

5．学生汇报，教师板书：6÷3=2，60÷30=2，600÷300=2。

6．提出问题：观察几个算式，你发现了什么？

7．学生回答：这几个除法算式的商都是2。

二、比较归纳，探究新知

1．引导发现。

（1）提出问题：大家观察的真仔细，你还能说出几道商是2的除法算式吗？

（2）学生自由汇报，教师选择板书：12÷6=2，24÷12=2，48÷24=2，6000÷ 3000=2，……

（3）引导思考：同学们说的真好！这些算式排的太乱，谁能把他们按一定的顺序排列呢？

（4）学生回答，教师板书：6÷3=2，12÷6=2，24÷12=2，48÷24=2，60÷ 30=2，600÷300=2，6000÷3000=2。

2．提出问题。

比较每个算式的被除数、除数和商：①从上到下看，是按照什么规律变化的？②从下到上看，是按照什么规律变化的？

3．集体讨论，归纳性质。

（1）学生小组讨论。

（2）教师引导交流。

①教师引导学生交流：从上到下看，是按照什么规律变化的？

学生举例说：6÷3=2到12÷6=2的变化规律。教师指出：像这样的变化过程，我们可以说：6÷3=2被除数和除数都扩大2倍，商不变。

②追问：其他几组算式的变化规律是怎样的？你能归纳它们的变化规律吗？

学生说出其他几组的变化情况后，试着归纳变化规律：被除数和除数都扩大相同的倍数，商不变。

板书：同时扩大，相同的倍数。

③教师引导学生思考：从下往上看，又是按照什么规律变化的？

④学生举例说明，引导学生通过分析比较算式中被除数和除数，得出：被除数和除数都缩小相同的倍数，商不变。

板书：同时缩小

（3）归纳性质。

①引导归纳：你们能把刚才我们发现的这两个规律用比较简洁的语言概括成一句吗？

②学生交流：被除数和除数同时扩大（或缩小）相同的倍数，商不变。

③揭示性质：这就是商不变的性质，前面要“在除法中”就更好了。这就是我们今天学习的内容——商不变的性质。（板书课题：商不变的性质）

（4）理解性质。

①教师质疑：请同学们说一说这个性质中哪些字或词比较关键，为什么？

②学生回答：同时，因为……；相同的倍数，因为……（板书作重点记号）

（5）回归情境。

思考：猴王是运用了什么规律来分桃“忽悠”了小猴子的？

三、多层练习，深化新知

1．不计算，判断下面哪个算式与“16÷8”的商是相等的？为什么？

（16×2）÷（8×2）

（16÷2）÷（8×4）

（16×4）÷（8×5）

（16＋2）÷（8＋2）

利用这些题目，引发学生的争论，让大家在争论中加深对商不变性质的理解。

2．在○里填运算符号,在□里填数。

800÷25=(800×□)÷(25×4)

2800÷400=(2800÷100)÷(400 ÷□)

36÷18=(36○□)÷(180○□)

在学生填数的基础上,引导发现“0除外”,完善对“商不变的性质”的理解。

3.根据3120÷260=12，很快说出下面各题的商。

312÷26=

31200÷2600=

1560÷130=

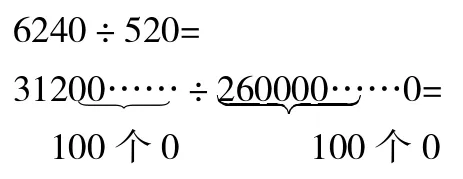
让学生利用“商不变的性质”灵活地简化计算。

四、课堂小结，延伸质疑

1．通过学习，你有什么收获？

2．你能举出一些商不变的性质在生活中的应用吗？

3．下课后，请手里卡片上算式得数与“28÷7=4”的得数相等的同学先出教室。（课前先发了一些写有除法算式的卡片）

【教学反思】

朴素而丰富的数学原理“商不变的性质”怎样从学生大脑中生长出来呢？本节课进行了一些尝试，并有了以下三点感悟：

一、探究欲望源于兴趣的激发

课堂应是点燃学生智慧的火把，恰到好处的问题情境，可以暴露学生认识中的矛盾，激发学生的学习兴趣，引发学生探究知识的欲望。在本节课，一开始教师先出示“猴王分桃”的趣味情境，讲述了一段生动的故事，学生非常感兴趣，并立即被吸引，从而认真思考故事中提出的问题。通过故事设疑，激发了学生探究新知的欲望，为后续学习做好了心理准备。

二、知识生长源于有效的建构

建构主义对学习持有这样的观点：知识是不能被传递的，而是基于主体经验的主动建构，强调学习者的主动作用，强调学习的主动性。对于“商不变的性质”学生并不陌生，因为学生在进行整十数的口算除法时，已经有所接触。本节课的关键是帮助学生完善对这一性质的认知。因此，在把握教学起点的情况下，首先通过问题情境激活已有经验；接着让学生自己说出商是2的除法算式，对这些除法算式进行整理、排序，引导学生观察、思考这些除法算式的变化规律，指导学生进行描述；再引导学生抽象、概括出商不变的性质，最后通过分层练习帮助学生深化理解性质，至此，完成了帮助学生对商不变性质从模糊认识到清晰理解的认知完善过程。学生在这个过程中主动探索，知识逐步生长。这一过程也是数学规则学习从具体实例感知——语言抽象概括——具体实例运用的建构过程。

三、新知内化源于深刻的理解

抽象的数学规则必须在具体的实例中加以运用，这样不仅能帮助学生理解数学规则，同时也发展了学生的数学应用意识。因此，在本课的巩固练习环节中，练习作了精心设计，由易到难，由浅入深：练习1注重对性质中关键词的理解，练习2引导学生发展扩大（或缩小）的倍数（0除外），练习3则运用性质进行简化计算，而课堂小结中说一说生活中运用商不变的例子，让学生体会数学与生活的联系。最后，请手里卡片上算式得数与“28÷7=4”的得数相等的同学先出教室，既巩固了知识，又检查了效果，多种途径帮助学生理解、内化新知。

与此同时也有几点思考：一是学生回答“你还能说出几道商是2的除法算式吗？”这个问题时，说出的算式是被除数和除数同时扩大（或缩小）倍数不是整数倍的算式，该怎样处理？是纳入研究范围还是放在一边？二是由于学生现阶段没有学习0为什么不能做除数，对为什么不能同时乘（或除以）0缺乏理解认识，因此，这里的教学如何处理也是值得思考的问题。三是本节课我们教给学生的是什么？我们交给学生的不仅是商不变性质这个知识，更重要的是研究商不变性质的方法。学生通过观察、比较除法算式后提出的猜想，实际是数学中的不完全归纳法，由于学生的知识水平有限没有证明猜想，但是这种方法对于学生研究其他数学问题是很有帮助的，也许这就是“数学是思维的体操”的体现吧。

冯胜华中科技大学附属小学邵承民武汉市硚口区武药小学）

责任编辑 廖林