波群内单个波的波陡分布与波破碎

高志一,文 凡,李 洁

(1.国家海洋环境预报中心 海洋灾害预警报技术重点实验室,北京 100081;2.中国海洋大学 物理海洋实验室, 山东 青岛 266003)

波破碎的研究是当今海浪研究中的热题。近年研究结果表明波群是影响波破碎的重要因素[1-4]。波群由一连串波高超过某一临界值的波构成,而波群中单个波的最大振幅出现位置对波的破碎具有重要影响。Banner等[5]研究认为：波群中单个波的振幅和波陡在波群中央达到最大,当单个波振幅超过临界值时,该波发生破碎。最大振幅的波出现在波群中央,意味着波群具有某种对称性。但如果波群结构前后不对称,波群前侧波动振幅将可能大(小)于后侧波动的振幅,在这种情况下,波群中最大波高可能出现在波群前(后)部,而不是在波群中央,波群前侧波动的波破碎率就大(小)于后侧。基于这种设想,本文对波群结构和波群中单个波的位置以及其对波破碎的影响进行了实验研究。研究中依据波包络线理论[6]研究波群,分析风浪波包络时间导数分布的结果表明：波群结构是不对称的,波群中波动的最大振幅出现在波群前部而不是波群中央,波群的这种不对称性导致波群前部单个波出现大波陡的概率大于后部单个波出现大波陡的概率。波群前部与后部单个波波陡的差异随谱宽度和平均波陡增大而增大,实验研究表明：波群前部单个波的波陡大于后部单个波波陡,因此导致波群中单个波在波群前部发生破碎的概率较大。由于波破碎对风浪成长等具有重要意义,而波发生破碎的位置与波群结构的不对称性有关,因此本文结果对风浪研究具有重要意义。

1 风浪实验

1.1 实验设置

实验室观测在中国海洋大学物理海洋实验室大型风浪槽中进行。风浪槽长65 m,宽1.2 m,高1.2 m。在风浪槽中取10个观测点观测风浪波面高度。观测点位置为7,10.7,14.35,18,21.7,25.4,29.05,32.75,36.4,41 m。在4种平均风速下进行实验：4,6,8,10 m/s(由设置在风浪槽 47 m处的风杯式风速计测得),同时在各个观测点进行同步的风场观测。实验时水深0.73 m。观测波面高度时采样间隔为0.0308 s,每个波浪观测记录长度为5 min。本文实验中录制了实验室风浪视频资料,以便用于研究波群中单个波发生破碎的频率。

1.2 波陡的计算

本文以ak表示波群中单个波的波陡,a为该波的波峰高度,k为该波的波数k=2π/L。L=gT2/2π[7],是单个波的低阶近似波长,周期T是相邻波谷之间的时间间隔。平均波陡为ak0=a0k0,其中a0=(2m0)1/2,其中m0为0阶谱矩,平均波数k0是谱峰频率对应的波数。用平均波陡对单个波的波陡进行归一化。

1.3 波龄的观测

实验中在各个观测点采用皮托管式风速计观测瞬时风速,皮托管风速计与测波仪固定于同一支架上,并由计算机控制可以上下移动、定位,定位间隔2cm,最低测点距下垫波浪浪尖约 2cm,由下至上共观测15层,每层风速采样 200次,采样间隔 0.02 s。使用最小二乘法拟和对数风速廓线并求出粗糙度和摩擦风速

其中z0为粗糙度,U*为摩擦风速,z为高度,κ为Karman常数,取0.4。再以上述公式计算z=10 m高度处的风速U10,由下式计算波龄σ：

其中Cp为谱峰频率波动的相速。

1.4 谱宽度的定义

本文研究中采用一般的谱宽度参数ε[8]

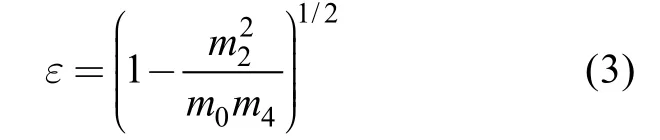
其中mi为频率谱的i阶矩。

1.5 波包络的计算

实验研究中采用 Hilbert变换方法求波包络,求波包络时滤波截断频率取0.5～1.5倍谱峰频率[6]。计算得到的波包络如图1中虚线所示。

图1 由Hilbert变换方法得到的波包络Fig.1 The envelope calculated by Hilbert transformation

1.6 波群定义

本文研究中采用 Kimura的波群定义[9]：波高超过某一临界高度的单个波构成波群。实验中将波峰高度超过水平ρ0的波浪序列定义为波群,临界水平取值为ρ0=(2m0)1/2。同时对波群内单个波编号,如图2为一个连长3的波群,即该波群包含3个单个波,按从左至右的顺序将它们编为第1,2,3号波动。

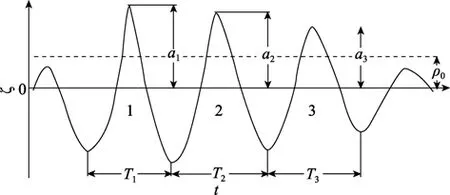
图2 连长为3的波群Fig.2 A wave group with three individual waves

1.7 波破碎

以波破碎产生的气泡作为波动发生破碎的示踪物(如图3)。如果测波探头前后半个主导波波长范围内出现气泡,则认为发生一次破碎事件,同一个单个波的波峰出现多个气泡仍然记为一个破碎事件。将波破碎率B定义为发生破碎的波峰个数与单个波总个数之比。实验室产生的风浪具有明显的群性,容易从视频资料中统计波群中单个波发生破碎的频率。

图3 波破碎形成的气泡Fig.3 The bubble(s) generated in the process of wave breaking

2 波包络时间导数分布的研究

迄今 Longuet-Higgins[6],Nolte和 Hsu[10],Ew-ing[11]等依波包线理论对海浪波群的统计性质进行了大量研究,如对波群平均历时长度、平均连长以及波群波包络上跨水平数的研究等。前人在其研究中一般都假定波群包络线具有对称结构,未注意波群包络线的不对称性问题。本节依波包络线理论来研究波群结构,研究结果表明波群具有不对称结构,即波群前部单个波振幅大于波群后部单个波振幅。

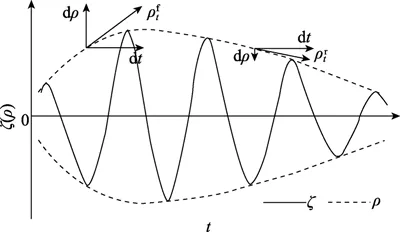
图4 波群前部和后部波包络的时间导数 和Fig.4 The time derivatives of the envelope in the front of and in the rear of a wave group (and )

按 Hilbert变换方法求出包络线ρ之后,采用线性差分计算波包络线时间导数ρt

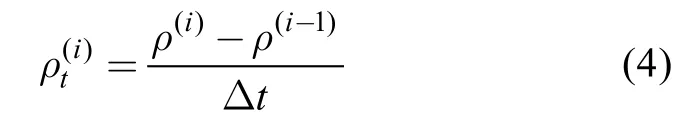
其中Δt为采样时间间隔,使用ρt的均方根σtρ将ρt归一化。

本文采用Gram-Charlier级数[12]拟合波包络时间导数的分布,Gram-Charlier级数为

图5 归一化的波包络时间导数分布Fig.5 The distributions of the normalized time derivative of wave envelope

图5为根据实验数据拟合得到的归一化波包络线时间导数分布。实测波包络时间导数分布系统地向左偏离正态分布,概率密度最大值出现在-1～0之间。0～2之间的概率密度低于正态分布曲线,2～4的概率密度高于正态分布;-1.5～0的概率密度高于正态分布,-3～-1.5的概率密度低于正态分布。大量实验结果都具有上述特征,这表明波群具有前后不对称的结构(波群前部包络线陡峭,后部包络线平缓)。

研究结果还表明波群结构的不对称性程度随谱宽度和平均波陡增大而增大。

图6和图7分别为偏度因子与谱宽度和平均波陡之间的关系。从图中可以看出偏度因子随谱宽度和平均波陡增大而增大(除圆圈圈出的点外)。对实验数据进行分析发现,被圈出的点对应的波浪有较高的破碎率,波破碎造成波群前部单个波振幅变小,因而波群前部波包络线振幅下降,造成波包络线不对称程度减小,因此这些点的偏度因子λ3值偏低。

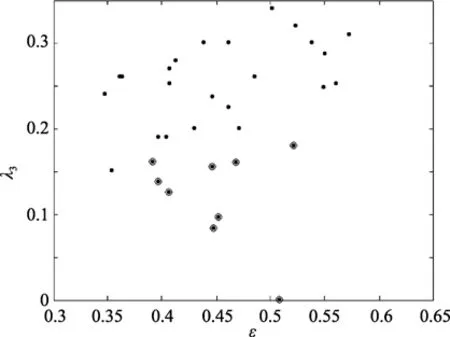
图6 偏度因子λ3与谱宽度之间的关系εFig.6 The relation between the skewness λ3 and spectral width ε

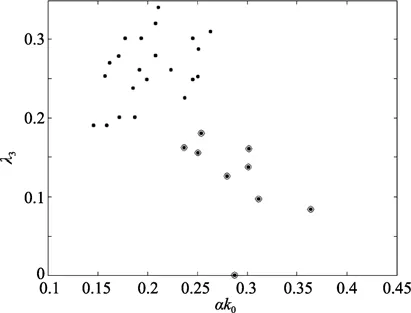
图7 偏度因子λ3与平均波陡ak0之间的关系Fig.7 The relation between skewness λ3 and the mean wave steepness ak0

波包络时间导数分布系统地向左偏离对称分布表明波群的包络线前部陡峭后部平缓,而不是前后对称的(如图4)。这对波群中最高单个波出现的位置有重要影响,从图4容易看出最大波高出现在波群前部。由于波动的波高与波陡之间存在密切联系,波群内最高单个波出现在波群前部可能造成波群内单个波波陡的累积概率分布与单个波在波群中的次序有关。

3 波群内单个波波陡分布的研究

研究结果表明,波群具有不对称结构,波群前部单个波振幅较大。又已知波群中单个波的振幅与波陡之间存在密切联系,这就引出一个问题：波群结构的不对称性对波群中单个波的波陡分布有什么影响？为研究这一问题需要研究波群中不同位置上单个波的波陡分布。这项研究对深入了解波破碎现象也具有重要意义[13-14]。

研究结果表明,波群前部单个波出现大波陡的概率大于后部单个波出现大波陡的概率;单个波的波陡分布与单个波在波群内的位置有密切关联;波群前部和后部的单个波波陡累积概率分布的差异(单个波波陡累积概率分布曲线的“张角”)随谱宽度和平均波陡增大而增大。

3.1 单个波波陡分布次序性的研究

对波群内不同序号单个波的波陡分布进行研究。结果表明,波群前部单个波出现较大波陡的概率大于波群后部单个波出现较大波陡的概率。

将同一波面记录上全部连长为N的波群分为一组,分别对第1到N号(编号方式见图2)单个波的波陡进行统计。统计结果如图8所示。图8为波群内单个波的波陡累积概率分布。从图中明显可以看出,序号越大的单个波出现大波陡的概率越小。大量实验结果都具有上述特征,这表明波群内单个波的波陡分布与单个波的序号有关。下面的分析将看到,单个波序号对波陡分布的影响与波龄的影响相当。

图8中显示波群内不同序号单个波的波陡分布曲线形式相似,单个波的序号越小其波陡分布曲线的位置越高(波群前部和后部单个波的波陡分布曲线之间的张角θ越大),这意味着序号越小的单个波的平均波陡越大,这将导致波群前部单个波的破碎率较大。

图8 单个波在波群中的次序与单个波波陡分布的关系Fig.8 The relation between the steepness distribution of individual waves and the position of the waves

3.2 单个波波陡分布与序号关系的研究

研究发现,单个波波陡分布与单个波在波群中的序号(编号方式见图2)有密切关联。单个波序号对单个波波陡分布的影响是不可忽略的。

图9为波群内单个波序号和波龄与单个波波陡分布的关系。图9 上图为同一风浪场中连长分别为2,3,4的波群中1号和2号单个波的波陡累积概率分布,图9下图为谱宽度相同波龄不同的两种风浪场波群内 1号单个波的波陡累积概率分布。比较上下两组图可以发现,连长2和3的波群内单个波的序号对波陡累积概率分布的影响大于波龄对波陡累积概率分布的影响,连长 4的波群内单个波的序号对波陡累积概率分布的影响与波龄对波陡累积概率分布的影响相当。图10采用了与图9不同的观测数据,得到的结论是相同的。大量实验结果表明,单个波序号对波陡分布的影响与波龄的影响相当,甚至超过波龄的影响。

图9 单个波次序和波龄对单个波波陡分布影响Fig.9 The influences of the position of the individual wave and wave age on the steepness distribution

3.3 谱宽度和平均波陡对单个波波陡分布影响的研究

实验结果表明波群结构不对称性的程度随谱宽度和平均波陡增大而增大,也就是说波群前部和后部单个波的振幅差异随谱宽度和平均波陡增大而增大。研究发现,波群前部和后部单个波波陡累积概率分布曲线的差异也随谱宽度和平均波陡增大而增大。

图11为平均波陡相同条件下谱宽度对单个波波陡分布的影响。从图中可见,谱宽度较大的波群中首个单个波波陡分布与末尾单个波波陡分布的差别(波群内单个波波陡分布曲线的张角θ)较大。大量实验结果都具有上述特征,这表明波群前后单个波陡分布的差异随谱宽度增大而增大。

图12为平均波陡较小情况下平均波陡对单个波波陡分布的影响。从图中可以看出平均波陡较小时(波破碎影响较小),平均波陡较大的波群中首个单个波波陡分布与末尾单个波波陡分布的差别(波群前部和后部单个波波陡分布曲线的张角θ)较大。

由于波破碎率随平均波陡增大而增大,波群前部单个波发生破碎的频率较大使该波的波陡减小。因此平均波陡增大时波群前后单个波波陡分布的差异不增大反而减小(如图13所示)。

图13为平均波陡较大(破碎率较大)情况下平均波陡对单个波的波陡分布的影响。从图中可以看出平均波陡较大时(波破碎影响较大),平均波陡较大的波群中首个单个波波陡分布与末尾单个波波陡分布的差别(波群前部和后部单个波波陡分布曲线的张角θ)较小。

大量实验结果都具有上述特征。这表明平均波陡较小时(波破碎影响较小),波群前部和后部单个波波陡分布的差别随平均波陡增大而增大;平均波陡较大时(波破碎影响较大),波群前部和后部单个波波陡分布的差别随平均波陡增大而减小。

图10 单个波次序和波龄对单个波波陡分布影响Fig.10 The influences of the position of the individual wave and wave age on the steepness distribution

3.4 单个波波陡分布信息熵的研究

将信息熵概念应用于波群内单个波波陡分布的研究,发现相同连长的波群中不同序号单个波波陡分布的信息熵不同。

3.4.1 波陡分布的信息熵

Shannon将Boltzmann熵的概念加以推广,引入信息熵的概念,用以表征随机过程中事件的不确定性程度。在某随机过程中若各事件发生的概率为p1,p2,….,pn信息熵定义[15]为

图11 谱宽度对单个波波陡分布的影响Fig.11 The influence of spectral width on the distributions of individual wave steepness

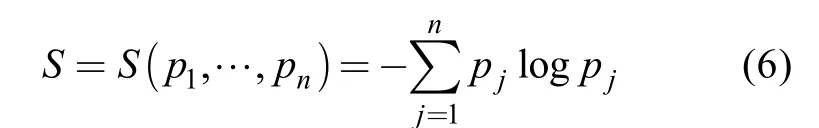
信息熵(6)通过概率分布pj定量地表征随机过程中事件发生的不确定性的程度。信息熵的值越大,事件发生的不确定性程度越高。

将实测的归一化波陡ak/ak0的取值范围划分为多个取值区间,统计归一化波陡在各个区间出现的概率(ak/ak0的取值范围为0.5～3,将其划分成10个取值区间)。ak/ak0出现在第j个取值区间的概率即为(6)式中的pj。根据(6)式计算出同连长波群单个波波陡分布的信息熵。

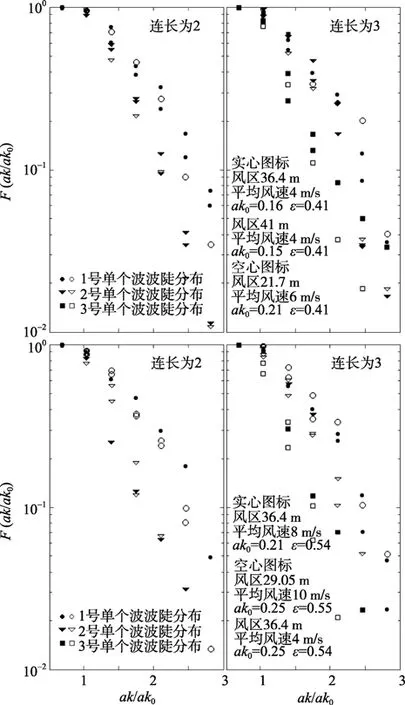
图12 平均波陡较小时其对单个波波陡分布的影响Fig.12 The influence of the mean wave steepness (with smaller values) on the individual wave steepness distribution

3.4.2 不同序号单个波波陡分布的信息熵

图14为连长2和连长3的波群内单个波归一化波陡ak/ak0分布的信息熵与谱宽度ε的关系。从总体趋势上看,连长为2的情况中1号单个波波陡分布的信息熵大于2号;连长为3的情况中1号单个波波陡分布的信息熵最大,2号次之,3号最小。由图14的结果可知,同样连长的波群中不同位次单个波波陡的统计分布是不同的。

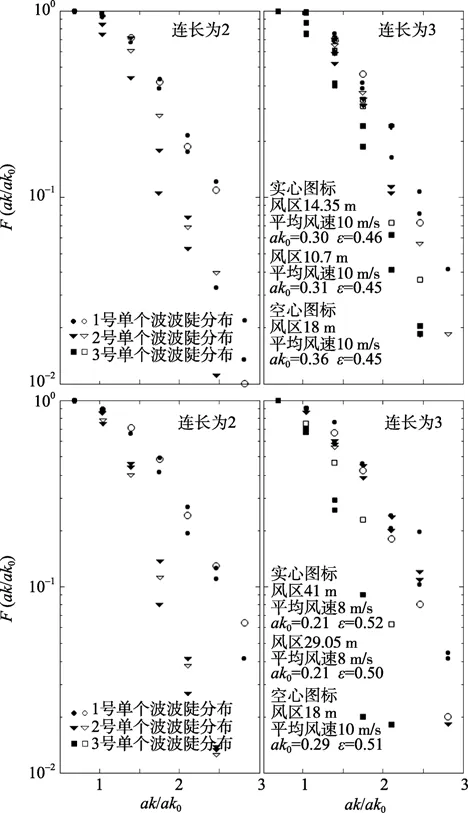
图13 平均波陡较大时其对单个波波陡分布的影响Fig.13 The influence of the mean wave steepness (with larger values) on the steepness distribution of steepness

4 波群中波破碎的研究

波破碎对大气-海洋之间热量和动量交换以及波浪谱的演化都有重要影响,对波破碎的研究具有重要理论和应用意义。近年对波破碎的研究结果表明,波群是影响波破碎发生的重要因素。Donelan等[1]和Holthuijsen[4]在外海观测时发现多数波破碎事件发生在波群内。Dold和 Peregrine[16]发现,波群内包含的单个波越多,发生波破碎的临界波陡越小。Banner等[5]提出,波破碎判据中应包含与波群性质有关的参量。然而迄今对波群中波破碎发生位置这一问题研究较少。

图14 连长2和3的波群内单个波波陡分布的信息熵与谱宽度的关系Fig.14 The relation between information entropies of the individual wave steepness distributions in wave groups and spectral width

实验结果表明,波群结构的不对称性(波群前部单个波的振幅较大)导致波群前部单个波出现大波陡的概率大于后部单个波出现大波陡的概率,也就是说波群内序号较小的单个波的平均波陡较大。由于波破碎与波陡密切相关,这意味着波群内的波破碎率很可能与波群内各波的序号(即各波在波群中的位置)有关。对这一问题进行研究的结果表明,波群前部单个波更容易发生破碎,波群前部单个波发生破碎的频率为后部单个波的 4倍。这一结果对深入了解波破碎现象具有重要意义。

实验中首先研究破碎率B与平均波陡之间的关系,实验结果表明波破碎率随平均波陡增大而增大(如图15),这与前人研究结果一致[5]。接下来研究波群中波动发生破碎的位置。统计波群内不同序号单个波发生破碎的次数,结果表明在各种连长的波群内波群前部单个波的破碎数高于后部单个波的破碎数(如表1)。其中连长2的波群内1号单个波破碎数为2号波的1.3倍,连长3的波群内1号单个波破碎数为3号波的4倍。这意味着波群前部的波动更容易发生破碎。

图15 破碎率B与平均波陡ak0的关系Fig.15 The relation between probability of wave breaking B and mean wave steepness ak0

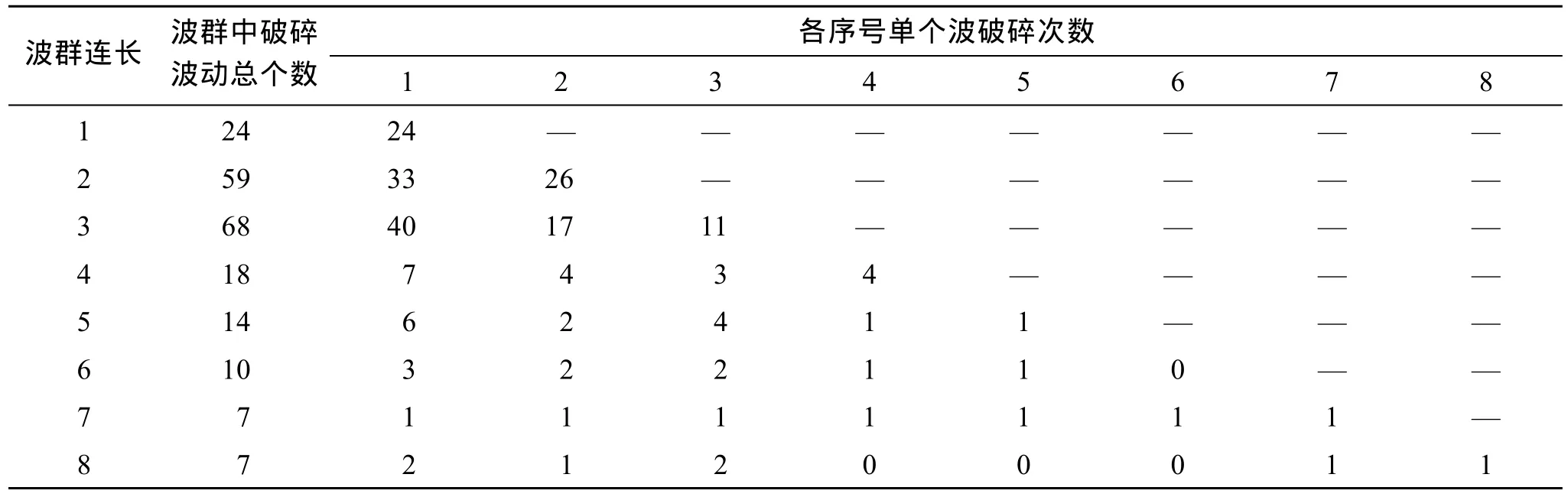
表1 波群中单个波发生破碎的次数Tab.1 Breaking times of individual waves in wave groups

波群前部单个波发生破碎的频率较大导致图6和图7中的数据散落。图16为波群前部单个波破碎率较大对波群结构不对称性程度的影响。图中所示波群内第一个单个波发生破碎,将该波的波峰削去(如图16中阴影部分所示)。本文实验中采用电容式测波仪观测波浪,该仪器只能记录水位的升降,波破碎事件在波面记录上就表现为波面高度下降。由这种波面高度记录计算得到波包络为图中长虚线ρb所示,若没有波破碎的影响波包络应为图中短虚线ρnb所示。容易看出波破碎造成波群结构的不对称性程度减小。这样便解释了图6和图7中的数据散落现象。同样道理可以解释图13中平均波陡增大波群前后单个波波陡分布差异减小的现象(波陡分布曲线张角θ减小)。

图16 波破碎对波包络线振幅的影响Fig.16 The influence of wave breaking on the envelope amplitude

5 结语

本文研究了波群结构对波群中单个波波陡分布和波破碎的影响。实验结果表明,波群具有不对称结构,波群内最高单个波出现在波群前部而不是波群中央;波群的这种不对称性导致波群前部单个波出现较大波陡的概率较大,且波群前部和后部单个波波陡分布的差异随谱宽度和平均波陡增大而增大;波破碎视频统计结果表明,由于波破碎与波陡密切相关,波群前部和后部单个波的波陡的差异导致波群前部的单个波更容易发生破碎(波群前部单个波破碎的频率是后部单个波破碎频率的 4倍),而不是波群中央的单个波更容易发生破碎。由于波破碎是风浪成长理论中的重要问题,而波破碎更容易发生在波群前部,因此本文结果对风浪研究具有重要意义。

[1]Donelan M A,Longuet-Higgins M S,Turner J S.Whitecaps [J].Nature,1972,239：449-451.

[2]Thorpe S A,Humphries P N.Bubbles and breaking waves [J].Nature,1980,283：463-465.

[3]Su M Y.Large,steep waves,wave grouping and breaking [C]//Webster W C.Proc 16th Symposium on Naval Hydrodynamics.Berkeley：ONR,1986.

[4]Holthuijsen L H,Herbers T H C.Statistics of breaking waves observed as whitecaps in the open sea [J].J Phys Oceanogr,1986,16：290-297.

[5]Banner M L,Babanin A V,Young I R.Breaking probability for dominant waves on the sea surface [J].J Phys Oceanogr,2000,30：3145-3160.

[6]Longuet-Higgins M S.Statistical properties of wave groups in a random sea state [J].Phil Trans R Soc Lond,1984,312(A)：219-250.

[7]文圣常,余宙文.海浪理论与计算原理 [M].北京：科学出版社,1984.

[8]Cartwright D E,Longuet-Higgins M S.The statistical distribution of the maxima of a random function [J].Proc Roy Soc London,1956,237(1209)：212-232.

[9]Kimura A.Statistical properties of random wave groups[C]// Billy L E.Proc 17th Int Conf on Coastal Eng.Sydney Australia,New York：ASCE 1980.

[10]Nolte K G,Hsu F H.Statistics of larger waves in a sea state [J].J Waterway,Port,Coastal Ocean Div,1972,105：389-404.

[11]Ewing J A.Mean length of runs of high waves [J].J Geophys Res,1973,78(12)：1933-1936.

[12]Huang N E,Long S R.An experimental study of the surface elevation probability distribution and statistics of windgenerated waves [J].J Fluid Mech,1980,101：179-200.

[13]Banner M L,Gemmrich J R,Farmer D M.Multiscale measurements of ocean wave breaking probability [J].J Phys Oceanogr,2002,32：3364-3375.

[14]Svendsen I A,Veeramony J.Wave breaking in wave groups [J].J Waterway,Port,Coastal,and Ocean Engineering,2001,127(4)：200-212.

[15]Guiasu S.Information theory with applications [M].London：Mc-Graw-Hill Inc,1977：1-439.

[16]Dold J W,Peregrine D H.Water-wave modulations[C]//Billy L E.Proc 20th Int Conf Coastal Eng.Taipei Taiwan,New York：ASCE 1986.