用于水下通信的电磁耦合系统的优化设计

(浙江大学 机械电子控制工程研究所,浙江 杭州 310027)

在深海的高压环境下,为了安全考虑,水下工作的深潜器和作业工具之间不能通过电缆直接相连,深潜器和作业工具间实现数据传输必须通过电磁耦合等非接触方式[1]。电磁耦合方式能够很好地满足水下非接触数据传输这一要求,相比于水下光通讯和声通讯,它结构简单、功耗低、尺寸重量较小、造价低廉,传输速率也基本能满足要求[2-3]。

电磁耦合方式利用电磁感应原理,数字信号通过调制后作为 RCL电路的信号源,使电感线圈产生和信号相关的交变磁场,而和该线圈耦合的电感线圈则产生感应电动势,最后由解调电路解调得到原数字信号,实现非接触式数据传输。这种电磁耦合信息传输方式传输角度很大,线圈间轴向通讯距离和径向通讯距离差不多,但磁场强度随距离增大而大幅衰减,传输距离很短。

本文提出了通信距离和线圈直径、匝数和载波频率之间的关系,并据此确定了电磁耦合系统优化设计的新方法,选择合适的载波频率,针对需要的最大通信距离设计出最小尺寸的线圈,确定线圈的匝数。

1 接口电路

检测线圈通讯性能的接口电路框图如图1所示。两个接口分别为深潜器端和工作器端接口,由两个电感线圈实现信号的耦合。两个接口的电路大致相似,均能实现信号的调制和解调功能,可双向发送和接收。图1中只表示单向数据的传输过程。电感线圈上的载波频率可以在 200～550 kHz范围内任意调节[4]。为使通过电感线圈的电流达到最大,能量有效利用,RCL电路必须达到谐振,即满足：

其中,f为载波频率,L为线圈的电感,C为串联的电容。

2 通信距离

2.1 决定系统通信距离的因素

原线圈的交变电流使线圈产生交变磁场,感应线圈中产生感应电动势。感应电动势的幅值达到一定值时解调电路才能够成功解调出信号,

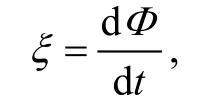
ξ和Φ分别为感应线圈的电动势和磁通,另

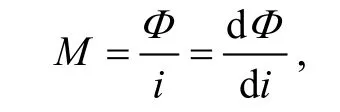
M为两个线圈间的互感,i为原线圈的电流。

若假定原线圈电流为i=Isin(2πft+φ),对于无铁芯圆柱形线圈则有,

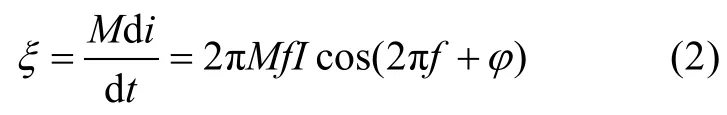
感应线圈感应电动势的幅值决定了能否通信,而线圈的感应电动势幅值是由互感M,载波频率f和原线圈电流幅值I共同决定的。考虑功耗因素,RCL电路的电阻限制了该电流幅值。同样,感应电动势幅值低于何值时解调电路不能解调出正确信号也是由接口电路决定的,这和接口电路的滤波和检波电路有关。在既定电路的条件下,M和f直接决定了系统的通信效果。

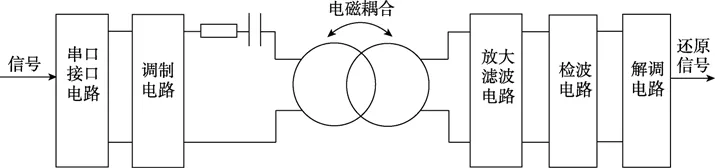
图1 接口电路示意简图Fig.1 Scheme of interface circuit

定义通信系数k=Mf,其中两线圈的互感M由于随着线圈间的距离增大而逐渐变小,因此k也随着线圈间的距离增大而逐渐变小。当k小到一定值时,两线圈间不能实现通信,定义这个值为klim,则klim值所对应的线圈距离就是系统的最大通信距离。不难看出,klim的大小由电路本身决定,它可以用来评定电磁耦合方式调制解调电路的优劣。已知klim,就可以通过线圈的直径、匝数、载波频率等得出 ICL系统的最大通信距离。

2.2 两线圈间互感的计算

两圆线圈的示意图如图2所示,a,b分别为两线圈的半径,d为两线圈间的距离。单匝共轴圆线圈的互感可以用如下公式表示：

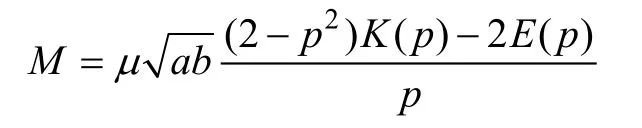
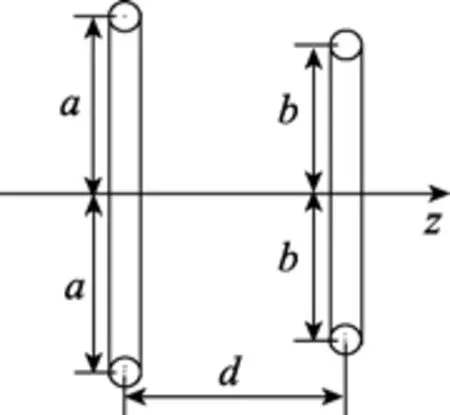
图2 共轴圆线圈间的互感Fig.2 Mutual inductance of coaxial round coils

线圈是有一定的截面尺寸的。计算发现,相同距离的线圈根据外径尺寸计算的互感和根据内径尺寸计算的互感两者的平均值与根据中径尺寸计算的互感极其近似,因此可以通过线圈的中径来对多匝线圈的互感值进行描述。多匝圆线圈的互感可以用如下公式表示：

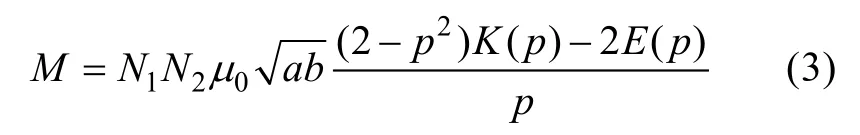
式中N1,N2分别为两线圈的匝数。

下文所提到的线圈直径均指线圈中径(内径和外径的平均值),线圈间距离即为平行的两线圈的轴向平均距离。

3 电磁耦合系统的优化设计

3.1 线圈自感对系统通信的影响

根据前文提出的理论,线圈的直径越大,匝数越多,系统的最大通信距离也越远。当匝数无穷大时,线圈间的通信距离也可以达到无穷远。此时,线圈的电感也变为无穷大值,为了达到谐振串联的电容就应该为无穷小值。实际上,由于干扰电容等其他因素的影响,为了能够使 RCL电路达到谐振,电感L不能取无穷大值。对于某一个固定的载波频率f,都有一个电感值Llim与之相对应。当电感线圈的电感小于Llim时,可以通过调节电容的方法使 RCL电路达到谐振,调出最大通信距离。当电感线圈的电感偏大时,无论如何调节电容都无法调出谐振,此时的最大通信距离很小,且不能保证两线圈在一定范围内都能实现通信。

通过实验发现,系统的载波频率越小,其对应的限制电感Llim越大,且达到谐振时的电感和串联电容的比值Llim/C越大。

3.2 线圈自感的计算

为了使线圈的最远通信距离达到最大,对于一定直径的线圈,其匝数要尽可能大,这时线圈的自感应达到或接近该载波频率对应的Llim值。这就需要对线圈的自感进行估算。空心原线圈的自感可以采用查表法和解析法来计算,也可以通过各种经验公式估算[6]。实际所缠绕的线圈截面近似为圆型,线圈采用0.44 mm的漆包线缠绕。线圈的自感和线圈的截面尺寸、直径和匝数相关,考虑到同种材料绕制的线圈截面尺寸和形状可以表述成匝数的函数,因此可以仅仅通过线圈直径和匝数估算线圈的自感。用专业的测电感电桥设备对多个同匝数不同直径的线圈和同直径不同匝数的线圈分别测量,可以得出该种直径漆包线绕制的线圈电感的经验公式：

其中D为线圈的直径,N为线圈的匝数,且同时要满足d≥50 mm,N≥10。

3.3 优化设计

前面论证过,要令系统的最远通信距离达到最大,线圈的电感应达到工作载波频率对应的Llim,这时线圈才可以在同直径情况下有更多的匝数,更好的通信效果。根据k的定义,提高载波频率,线圈直径、匝数都能获得更好的通信效果。但实际存在着电感对线圈直径和匝数的限制,提高载波频率,Llim下降,同直径线圈可缠绕的最大匝数变小。

根据通信系数的定义有

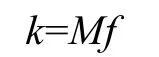
对于同直径,距离相同的线圈,若两线圈匝数均为N,则根据公式(1)有

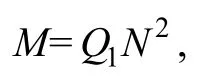
Q1为某一固定常数,又根据公式(3),则,

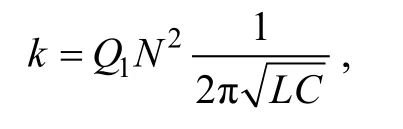
若令L/C=a,

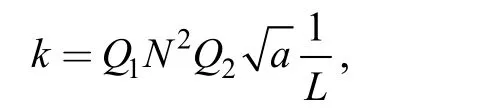
Q2为某一固定常数,又因为L约和线圈匝数的平方成正比,则,

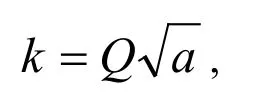
Q为某一固定常数。

由此可见,a值越大,同直径的线圈同距离时k越大,因此其最大通信距离也越远。因为当载波频率越小时,a所能取到的值越大,对应的同直径的线圈最大通信距离越远。由于载波频率减小最大通信速度也会减小,于是,对于该接口电路,综合考虑通信距离和通信速度,载波频率选为接口电路频率可调范围内的最小值200 kHz,此时测得对应的Llim值为4 570 μH。根据线圈间互感的计算和线圈自感的计算,通信系数的定义及测得的klim值 85 μH·kHz(空气中测得,测定方法如实验所示),我们可以得到优化设计方法设计的线圈最大通信距离和线圈直径间的关系,如图3所示,此时的线圈匝数如图4所示。

图3显示了按照最优化设计方法,最大通信距离和线圈直径近似成一次线性关系。实际应用中可以根据需要的最大通信距离确定线圈直径,然后根据图4确定线圈匝数,通过改变电容值达到谐振就可以得到最优的通信距离。

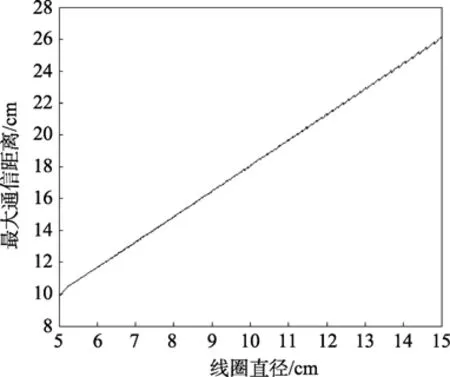
图3 最优时最大通信距离Fig.3 Maximum communication distance for optimum strategy

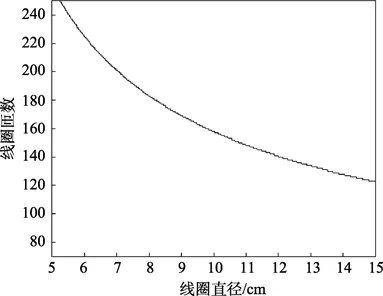
图4 最优时对应的线圈匝数Fig.4 The number of coils for optimum strategy

4 实验结果

为了表明线圈的互感和载波频率直接影响系统通信距离并测出接口电路的klim值,分别对同匝数不同直径的线圈在相同载波频率下的最大通信距离和同线圈对在不同载波频率下的最大通信距离进行了测试。潜器端通过串口和PC连接,工作器端和一种采样器电路连接,采样器电路对接收到的数据处理并返回数据,当 PC接收到的数据有明显错误或接收不到则说明通信失效。传输介质选用实现比较方便的空气介质。测量最大通信距离时,两个接口电路调制波形的载波频率必须要预先调为某固定值,并将图1中的电容换为可调电容,通过调节可调电容使RCL电路实现谐振。测量线圈间最大通信距离时,要保证两个线圈平行且同轴,逐渐增大两线圈间的距离并分别调节两接口电路上的可调电容达到谐振,使线圈间的通信距离可以达到最远。最大通信距离测量实验如图5所示。

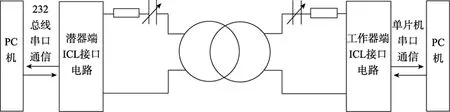
图5 最大通信距离测量实验Fig.5 Measurement of maximum communication distance

图6为在载波频率f=300 kHz下,五组同为100匝的不同直径的线圈的通信系数随线圈距离变化的曲线。图7为线圈直径为66.5 mm,匝数为100匝的线圈在不同载波频率下的通信系数随线圈距离变化的曲线。曲线为通过k的定义计算得出的理论曲线,▽符号对应的线圈距离是该对线圈在该载波频率下实际测量的最大通信距离。通过图6的实际测量结果,我们可以看出▽符号近似成一条水平直线,这条直线对应的通信系数约为 85μH·kHz,即可以看做为klim值,该线和曲线的交点对应的是该对线圈在该载波频率下的理论最大通信距离。从图6和图7看出,理论和实际的最大通信距离相差不大,最大偏差值小于1cm。得到klim,我们就可以定量地较精确地计算出线圈的最大通信距离。

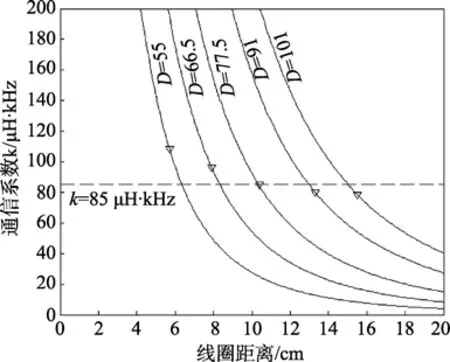
图6 线圈互感对通信距离的影响Fig.6 The influence of mutual inductance on communication distance

图7 载波频率对通信距离的影响Fig.7 The influence of carrier frequency on communication distance

采用耦合线圈的优化设计方法,根据图3和图4的最大通信距离和线圈直径,线圈匝数的关系,我们设计了几组不同直径的线圈,其理论和实际测量的结果如表1所示。

本次实验只针对空气介质进行了实验。海水对电磁信号的衰减远大于空气介质,且海水的导电系数越大,载波频率越高,信号衰减得越剧烈。现在还没有公式来描述海水对不同频率的电磁波的衰减情况,但不难确定的是,这种在空气中采用优化设计方法设计的线圈由于选用低载波频率,针对具体的水下情况也是最优的,只是通信距离可能发生变化。如果要精确的计算出通信距离需要测出该载波频率下该导电系数水体下的klim值。

表1 优化设计线圈最大通信距离Tab.1 Maximum communication distance between coils for optimal design strategy

5 结论

本文提出了通过通信系数来评定电磁耦合通信系统通信效果的方法,确定系统的最大通信距离,并对影响最大通信距离的因素进行了讨论,提出了一种最优的线圈设计方法：(1)通过对若干线圈的最大通信距离实验确定电路的klim值。(2)当线圈的直径和匝数都被限定时可以通过提高载波频率提高通信距离,直到无法调出谐振,即线圈电感达到该频率下的Llim。否则载波频率应根据情况,尽可能选择可调定范围内的最小值,测定该载波频率下的Llim。(3)确定线圈的自感随直径和匝数变化的公式。(4)绘制图3、图4的曲线,根据需要的最大通信距离确定线圈的直径和匝数。

此确定线圈最大通信距离的方法和线圈优化设计的方法不仅适用于圆线圈的电磁耦合通信,对于各种形状的线圈也同样适用。

[1]陈鹰.海底热液科学考察中的机电装备[J].机械工程学报,2003,38 (增刊)：207-211.

[2]刘飞,陈奇,补家武.ICL通讯在海底静力触探中的应用与研究[J].科学技术与工程,2008,8(12)：3110-3114.

[3]Fornari D,Bradley A,Humphris S.Inductively coupled link (ICL) Temperature Probes for Hot Hydrothermal Fluid Sampling From ROV Jason and DSV Alvin [J].Ridge Events,1997,8(1)：26-31.

[4]赵伟.深海非接触式双向信号传输技术研究[D].杭州：浙江大学,2004.

[5]王增和,王培章,卢春兰.电磁场与电磁波[M].北京：电子工业出版社,2001：113-115.

[6]贺开华.空心圆柱线圈电感计算方法的比较[J].船电技术,2006,26(6)：41-43.