基于电力线信道的一类OFDM盲同步算法的改进
王季立,贾振红,覃锡忠,李 涛,赵君凯
(①新疆大学 信息科学与工程学院,新疆 乌鲁木齐 830046;②中国移动通信集团新疆有限公司,新疆 乌鲁木齐 830091)
0 引言
随着通信技术的发展,人们在追求高速率和高可靠性数据通信的同时,也越来越重视通信成本的降低。利用电力线作为传输媒介,无需另外铺设通信线路,可以有效降低通信成本。但电力线信道具有线路衰减大,噪声干扰强,多径传输和频率选择性衰落严重的特点,会严重影响信号传输质量。OFDM技术作为一种高效的调制技术,以其抗干扰能力强,带宽利用率高,抗频率选择性衰落的特点,为实现高速低压电力线载波通信提供了一个有效的解决办法。然而,OFDM系统对同步误差较为敏感,因此准确的定时估计是实现OFDM系统的关键。目前已有大量文献对OFDM通信系统的同步技术进行了探讨,算法主要分为两类,一类是基于导频信号的数据辅助估计,这类算法性能好,但降低了系统传输效率;另一类是基于循环前缀的盲估计[1-4],虽然估计精度差,却提高了传输速度。最大似然估计(ML)算法[1]作为一种典型的盲同步算法,得到了广泛的应用与研究。在原ML算法基础上,人们提出了多符号ML算法[2],基于信道估计的ML算法[3],及简化的ML算法[4]等,但ML类算法是在高斯白噪声信道中推导出来的算法,不适合于多径效应明显的电力线信道。针对具有固定拓扑结构的电力线信道中时延扩展数值可以测定[5],电力线通信中没有多普勒频移的特点,在原ML算法,多符号以及简化的ML算法基础上提出了适合于电力线信道的盲同步算法,具有较高的估计精度,改变了原ML类算法在电力线信道中估计精度差的缺点,但同时又没有降低系统传输效率,为ML算法能推广应用在基于OFDM的电力线通信中提供了理论支撑。
1 电力线信道仿真模型
1.1 多径模型
德国学者 M.Zimmerman基于信道测量结果的基础上,提出了一种电力线信道多径模型的解析式[6]

式中i是路径号,gi为路径i的加权系数,a0,a1和k是衰耗参数,di为第i条路径的长度,vp为信号在电力线信道中的传播速度,对于介电常数εr≈4的绝缘材料(PVC),电缆的相位速度大约为1.5×108m/s。
1.2 噪声模型
按照Zimmermann.M提出的电力线中噪声的建模方法对三大类主要噪声(稳态背景噪声,脉冲噪声,窄带噪声)分别进行建模,仿真出的合成的电力线内噪声的时间域波形如图1。

图1 电力线信道中的合成噪声
2 同步算法
2.1 基于循环前缀的ML类同步算法及理论分析
以简化的符号ML算法为例,设传输的一个OFDM符号包含N个子载波,循环前缀长度为L,单位为抽样间隔,在输出段观察2N+L个连续样值r(k),得到自相关函数 c(θ) 。

时间定时和频率偏移表达式为[4]∶
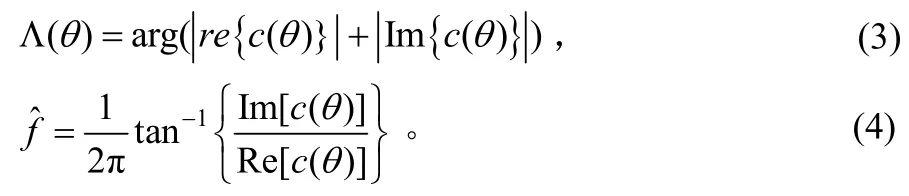
通常,为了取得较精确的定时效果,可以取当前的定时和前面几个符号的定时平均。然而ML类盲同步算法不适合于应用于具有多径效应的电力线信道中。理论分析如下:
在电力线信道中,存在多径效应,发送的信号经过M条独立路径到达接收端,因此,在k时刻,接收端接收到的信号可以表示为[7]:

其中s(k)是发送的OFDM信号,c(k,τ)是电力线多径衰落过程,n(k)是电力线信道中各种噪声的集合,每径延时为τm(m=1~ M),并设τm中最大为τmax,最小值为τmin,则时延扩展 τM=τmax-τmin。因为循环前缀是OFDM周期内后面一部分数据的复制,所以:

其中L是保护间隔时间段,l是整数,T为OFDM符号周期。由 r(k+T−L)减去r(k)得∶

其中,ndif=n(k+T)-n(k),因为在电力线通信中不存在多普勒频移以及当lT+τM≤k≤lT+L时,r(k)不受符号间干扰(ISI)的影响,所以当lT+τM≤k≤lT+L时,数值c(k+T,τm)-c(k,τm)可被认为是 0。且信噪比比较高时,差值ndif(k)几乎为零。由式(7),所以,当 lT+τM≤k≤lT+L时,且信噪比比较高时,rdif(k)几乎为零。也就是说,经过电力线多径衰落信道传输后,在高信噪比下,循环前缀中没有受到 ISI影响的那部分数据仍然和其T−L时刻后的数据具有很强的相关性。而ML类算法是用循环前缀的全部L个样值和其N(FFT/IFFT点数)个样点之后的L个样值做相关,如公式(3)、式(4)所示。如前分析,在电力线多径衰落信道下,循环前缀的一部分采样点(lT≤k≤lT+τm)必然受到 ISI的影响,使用循环前缀的全部L个采样点做相关势必会影响定时估计的精度。而ML算法载波频率偏移估计(CFO)是依赖于准确的定时估计的,若定时估计不准,载波频率偏移估计也将不精确。
2.2 基于电力线信道的改进的OFDM盲同步算法
与无线信道不同的是,对有一定拓扑结构的电力线信道而言,时延扩展在数值上相对稳定,循环前缀中受ISI影响的码元数目也就可以确定。这里的算法采用那部分不受 ISI影响的样值和其N个样点之后的样值作相关运算,按照前面的分析,它们的相关性应该很强,尤其是在高信噪比下。设由于时延扩展的存在,循环前缀中受ISI影响的码元数目为num。这里改进的算法,就是用循环前缀中那部分不受符号间干扰的码元和其后面T−L时刻后(N个样点后)的码元作相关运算 ,代替原 ML类算法中用所有的循环前缀的样点和其后面的样点作相关运算。因为采用新的算法后,峰值将会出现在lT+τM+ 1时刻(代替原来的(lT+1))时刻,所以定时估计还要减去num。以简化ML算法为例,自相关函数变为:

新的定时估计和频偏估计分别为:

设系统设计的比特速率为 v,经过测量和计算时延扩展为τ,每个子载波所携带的有用信息为b,由于存在时延扩展,循环前缀中受符号间干扰影响的码元数目为num。

3 仿真分析
为了验证以上算法在电力线信道中的有效性,有代表性地选取 Zimmermann.M 经过测量计算得到的四径模型(第一径是最强径)和十五径模型(第一径非最强径)来作为多径仿真模型[6](表1)。
参考信道1和参考信道2的衰减参数都为 k=1,a0=0,a1=7.8×10-10,以参考信道 2计算为例,如果信号在电缆中传播速率为1.5×108m/s(若介电常数为4),经计算时延扩展为0.773 µs,采用编码速率为1/2的卷积编码,4QAM调制,则每个子载波携带的有用信息为1 bit。若所设计的比特速率为10 M/s,按照公式(10),由时延扩展所延迟的码元个数为77,取保护间隔长度为256,FFT/IFFT点数为1 024。在MTLAB下仿真,分别在参考信道1和参考信道2下画出ML算法,多符号ML算法(取为8个符号),简化的ML算法以及它们的改进算法的时间估计均方误差,和频偏估计均方误差曲线。其中在信道1中计算num时,第四径忽略不计(因为第四径加权系数相对前三径很小)。考虑到简化 ML算法定时精确不高,信道2中简化的ML算法和改进的简化ML算法的定时取为前后三个符号的定时平均。

表1 电力线多径模型参数
从图2和图3可以看出在第一径为最强径的参考信道1中,只有简化的ML算法在定时估计和频率偏移估计上与原简化算法性能相当,而改进的原ML和多符号ML算法在高信噪比时(这里≥12 dB),在定时估计和频率偏移估计方面都比原算法好,在低信噪比时,性能相当。从图4和图5可以看出,在参考信道2中,由于多径效应明显,两类算法在低信噪比下性能都较差,但在高信噪比下(这里≥6 dB),改进的ML类算法均比相应的原算法好的多。尤其是改进的多符号ML算法,在多径效应明显的15径电力线信道中,在较高信噪比下仍然可以达到理想的定时效果。从仿真结果看,在第一径非最强径的多径模型中,原ML类算法定时效果差。原因是在第一径为非最强径的情况下,原ML类算法很容易发生定时偏移,定位在最强径上,从图6就可以看出。而现提出的算法则更容易定位在第一径上,而非最强径上,有效地克服了原ML类算法的不足,而且运算时间相对减少。图6为15 dB下信道2中的定时偏移概率曲线。

图2 信道1下的定时估计均方误差

图3 信道1下的频率偏移估计均方误差

图4 信道2的定时估计均方误差

图5 信道2下的频率偏移估计均方误差

图6 15 dB下信道2中的定时偏移概率曲线
4 结语
通过理论分析和仿真,可见这里在 ML类算法基础上,改进的盲同步方法在电力线信道中取得了不错的定时效果和频率偏移估计效果,尤其是在高信噪比以及第一径为非最强径时,算法的改进效果尤其明显,而且改进的算法计算量较少,仿真结果表明,该方法能较好的适应电力线通信的需要。
[1] van de BEEK J J,SANDELL M,BORJESSON P O.ML Estimation of Time and Frequency Offset in OFDM System[J].IEEE Trans.on Signal Processing,1997,45(07):1800-1805.
[2] TIEJUN L V, JIE Chen.ML Estimation of Timing and Frequency offset Using Multiple OFDM symbols in OFDM symbols[C].USA:Global Telecommunications Conference,2003: 2280-2284.
[3] HAO Zhou,MALIPATIL A, HUANG YIH-FANG.OFDM Carrier Synchronization Based on Time-Domain Channel Estimates[J].IEEE Trans. on Wireless Communications,2008,7(08):2988-2999.
[4] SHARMA N, PAPADIAS C B.Reduced-complexity ML Decoding of Rate 6/8 and Rate 1 Linear Complex Space-time Codes for up to Eight Transmit Antennas with Phase Feedback[J].IEEE Signal Processing Letters,2005,12(08):565-568.
[5] OH HUI-MYOUNG,CHOI SUNGSOO,KIM Young Sun,et al.A Systematic Technique for Esimating Multipath Parameters of Power-line Communication Channel[C]// IEEE. IEEE International Symposium on Power-Line Communications and Its Applications,Italy: IEEE, 2007:261-266.
[6] MANFRED Z,KLAUS D.A Multipath Model for the Power Line Channel[J].IEEE Trans Commun,2002,50(04):553-559.
[7] Kenkichi Takahashi, Takahiko Saba.A Novel Symbol Synchronization Algorithm with Reduced Influence of ISI for OFDM Systems[J].IEEE Global Telecommunication Conference,2001(01):524-528.

