一种三次均匀B样条曲线快速反算的方法＊

李道军，邬向伟

(1.郑州职业技术学院，河南 郑州 450121；2.中州大学，河南 郑州 450044)

在计算机辅助几何设计(CAGD)实践中，常遇到设计者事先并不知道控制多边形顶点的位置，而只知道曲线上的某些型值点的情况。从设计角度上来说，通常考虑的是曲线的大致形状，而非控制多边形的大致形状。为了构造B-spline曲线，就需要由已知的型值点反算出控制多边形的顶点。在实际工程应用中，B-spline曲线的反算过程所涉及到的计算量很大，因此讨论B-spline曲线的快速反算算法有着很重要的意义[1]。

对于三次均匀B-spline曲线的反算，朱心雄[2]给出了一种计算速度快且易于编程的反算控制顶点的迭代方法，可以得到在允许误差范围内的C2连续曲线。而参考文献[3]通过A-1的研究对三对角矩阵提出了一种优于追赶法和LU分解法的求解方法。但是它们都是以两端曲率为零作为边界条件，可能出现人们所不希望看到的曲线在端点处不连续的现象。针对B-spline曲线的反算过程计算量大，重构曲线端点处曲率不连续的问题，本文提出了一个有效的解决办法，并在Matlab[4]中予以编程实现，大大降低了程序的复杂性，提高了运算效率，并使重构所得曲线的两个端点处曲率不为零，至少满足了一阶连续。

1 反求B-spline曲线

为了使一条k次B-spline曲线通过一组数据点qi(i=0，1，…，m)，反算曲线时，一般使曲线的首末端点分别与首末数据点一致，将内数据点依次作为样条曲线的分段连接点，则数据点qi将依次与B-spline曲线定义域内的节点一一对应，即数据点qi有节点值uk+i(i=0，1，…，m)。该B-spline插值曲线将由 n+1个控制顶点 di(i=0，1，…，n)与节点矢量 U=[u0，u1，…，un+k+1]来定义。 其中，n=m+k-1，即控制顶点数目要比数据点数目多出k-1个，共有m+k个未知顶点。由端点插值要求，应取k+1重节点端点的固支条件，又取规范定义域。于是u0=u1=…uk=0，un+1=un+2=…un+k+1=1。

以反算三次均匀B-spline曲线为例，曲线的定义域为u∈[u3，un+1]，曲线的控制顶点应有 n＝m+3个。 则 B-spline曲线方程可表示为：

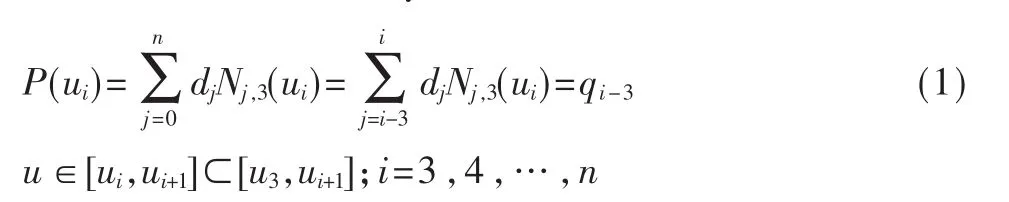
式中总共有m+1个线性方程组，但有n+1个控制顶点未知量。因此，要想得到唯一解，需要另外补充两个方程，这两个方程一般由边界条件给定。边界的补充条件有多种形式，如给定两端点的切向量、自由端点条件、虚节点条件和抛物线条件等，实际应用中根据具体情况选取适合的边界补充条件。有了补充方程，即可用迭代法或追赶法等求解所建立的线性方程组。

2 快速反算算法

将定义在每一个节点区间上用整体参数u表示的B-spline基变换成用局部参数 t∈[0，1]表示，则三次均匀B-spline曲线段的矩阵表示为：

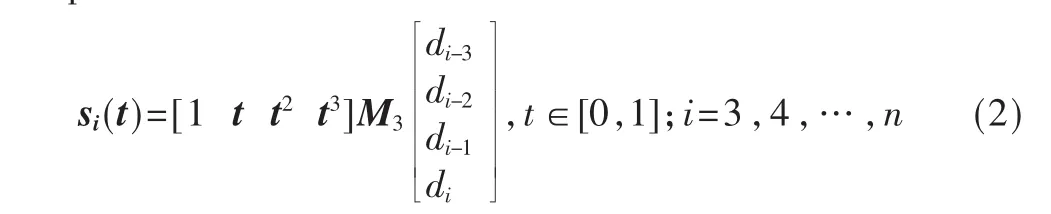
式中，[1 t t2t3]M3为三次均匀B-spline基的矩阵表示，M3为三次B-spline基函数系数矩阵，表示为：

补充边界条件：由均匀B-spline曲线的局部性质可知， 数据点的端点 P1与 d0、d1、d2、d3有关，Pn与 dn+1、dn、dn-1、dn-2有关。边界条件的补充除上述选用端点曲率为零外，还有两种方法：(1)令d0、dn位于其相邻的其他三个控制顶点所确定的抛物线上，这样能保证两个边界点的曲率不为零，但缺点是边界处卷曲过大；(2)令d0、dn位于其相邻的其他三个控制顶点的反向延伸直线段上，但不足之处是两个边界点的曲率也为零。比较好的方法是令d0、dn分别等于与其相邻的其他三个控制顶点所确定的抛物线及反向延伸直线的平均值，即：

由几何可知，三次均匀B-spline曲线在节点处，数据点与控制顶点之间有下列关系：

那么在Matlab中求解式(8)线性方程组将非常简单，本文用直接法进行求解，只需输入A和P，然后进行矩阵左除，即D=AP，即可输出方程组的解D=[d0d1…dn+1]T。需要说明的是，由于矩阵A中n一般很大，且元素多为非零元素，故储存时易用稀疏矩阵形式。 上述算法部分Matlab程序如下：

%输入数组 A，数据点 qi，i=1，2，…n；qx、qz分别为其坐标；

求出控制顶点后，再由式(3)即可求出参数定义域内任意节点上的数据点值，从而也就求出了所需曲线。

利用上述算法对图1所示经过预处理后的数据点进行运算，图2所示为反求的控制顶点，图3为上述算法重构的曲线。上述均匀三次B-spline曲线反求算法，可扩展到均匀双三次B-spline曲面控制网格顶点的反算。

[1]刘德平.逆向工程关键技术及其应用研究[D].西安：西安电子科技大学，2008.

[2]朱心雄.自由曲线曲面造型技术[M].北京：科学出版社，1999.

[3]吴光亚，王小华.反求三次B样条曲线控制顶点的一种快速算法[J].杭州电子科技大学学报，2005，25(3)：64-66.

[4]王学辉，张明辉.Matlab 6.1最新应用详解[M].北京：中国水利水电出版社，2002.