单领航者相对位移测量的多自主水下航行器协同导航

李闻白，刘明雍，张立川，刘富樯

(西北工业大学 航海学院，陕西 西安710072)

0 引言

随着人工智能理论、传感器技术和微计算机技术等的不断成熟和发展，具有感知、思维和动作能力的自主水下航行器(AUV)在军事和民用领域得到了广泛的应用，如水下情报搜集、远程水下攻击、深海资源勘测和海底光缆铺设等。就当前的技术而言，水下导航问题仍然是发展AUV 所面临的主要挑战之一［1］。导航系统必须提供远距离及长时间范围内的精确定位、速度及姿态信息，受AUV 自身的体积、质量、能源的限制及水介质的特殊性、隐蔽性等因素的影响，实现AUV 的精确导航是一项艰巨的任务［2］。

长基线(LBL)、短基线(SBL)和超短基线(USBL)系统作为三种传统的水下导航方法，已被广泛应用于潜艇和AUV 的实时导航与定位。这些系统的定位精度较高，但其中的一系列不足之处也是明显存在的［3-4］。以常用的LBL 为例，布放、标定和回收水下传感器基阵需耗费大量的时间、人力和物力，使用成本较高;此外，针对AUV 执行任务区域的不同，上述布放和回收工作需重复进行，制约了AUV 的活动范围。SBL 和USBL 需要母船支持，减少了AUV 的灵活性和隐蔽性。

出于以上考虑，研究人员提出了利用多个AUV间的相互合作实现协同定位的导航方法［5］。它使得导航信息能够分享，且摆脱了基阵(母船)的束缚，使用区域灵活，成本较低。通常多AUV 的协同导航采用主从式(Leader-Follower)，主AUV(领航者，Leader)装备有高精度的导航通讯设备(如GPS、磁罗盘、多普勒速度仪、深度计、水听器等)，从AUV(跟随者，Follower)配备的传感器精度相对较低。利用AUV 间的水声通讯，可以测量出各个不同时刻主、从AUV 间的相对位置信息，AUV 在各采样周期内的相对位移由自身的航位推算获得。根据上述信息并结合AUV 的运动学方程，利用扩展的Kalman滤波(EKF)方法就可以求取各从AUV 在不同时刻的定位估计。

为将系统复杂度及对量测手段的要求减到最小程度，人们提出了用一个领航者，仅利用距离信息的协同导航方法［6］。Bahr［7］等研究了单领航者AUV的协同导航，给出了基于极小化代价函数的CN 导航算法(CN-Algorithm)，但该算法对代价函数中Kullback-Leibler 距离(KL divergence)的求解过于复杂，没有考虑定位解算的实时性。Gadre［8］等通过单AUV 领航者与单固定信标相结合的导航方法来提高定位精度，给出了基于EKF 的协同导航算法，但固定信标的引入制约了AUV 的活动范围，同时减少了隐蔽性。Baccou［9］等采用领航者、跟随者AUV 间的适当机动来解决单个距离信息求解不充分的问题，通过设定初始化机动路径，利用Levenberg-Marquardt 方法(LM-Algorithm)优化协同导航EKF 算法中的滤波初值，并以此提高定位精度。但是，LM优化算法的收敛性与自身迭代初值的选取密切相关，不适当的初值往往导致其收敛到错误结果，因此在实施过程中至少需要选取50 组以上的不同初值进行迭代试验，利用统计方法筛选出最终的正确结果，这将使得算法的复杂性大为增加，从而降低导航算法的实时性与稳定性。

本文针对上述研究中存在的问题，结合单领航者AUV 协同导航系统的定位原理和运动学模型，基于相对位移测量、航位推算信息及相邻时刻主、从AUV 间相对位置的几何关系，提出了一种多AUV协同导航算法。该算法的原理直观、简捷，具有较高的定位精度，同时兼顾了导航解算的实时性要求。仿真结果验证了该算法的可行性和有效性。

1 数学模型

主、从AUV 均配备有各自的导航系统，其中包括磁罗盘、多普勒速度仪和水听器等传感器。如图1所示，tABk时刻AUV A、AUV B 间的距离为rAB(tABk)，其中k 表示A、B 间的第k 次数据传输;A、表示tAkB时刻AUV A 的推位B 间的航位推算信息在tAkB时刻实现交换，pADR(tAkB)=导航位置坐标，由A 的航位推算系统获得。

理论分析可知，由(1)式可以确定AUV B 的位置坐标(xB1，yB1)，而依次累加ΔpB12，ΔpB23…即可求得后续时刻AUV B 的位置坐标更新。进一步，方程组(1)存在唯一解的必要条件是向量组［xA1，yA1］T，和［x3A+Δx1B3，y3A+Δy1B3］T线性独立。也就是说，AUV A 和AUV B 不能以相同的速度沿同一方向平行航行，否则协同导航问题将无法求解(此时协同导航系统全局不可观测)，这与已有的研究结果是吻合的［8］。

在实际应用中，利用代数方法或数值算法通过(1)式直接求解(xB1，yB1)是不被采用的，这将导致(xB1，yB1)敏感地依赖于系统的输入(当系统近似不可观测时尤为显著)从而失去意义。因此，设计适当的EKF 导航算法是可行途径，在下一节中具体展开讨论。

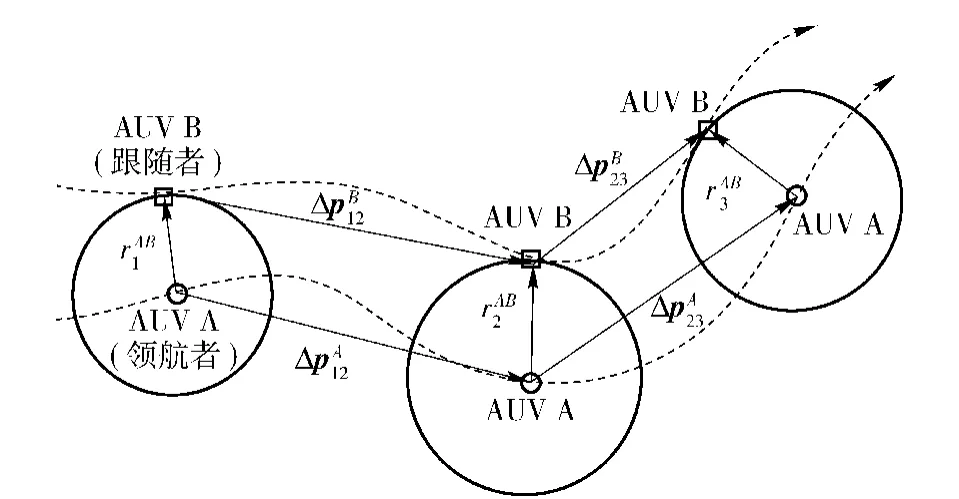
图1 主从式多AUV 协同导航系统Fig.1 Leader-Follower cooperative navigation system of multiple AUVs

2 协同导航算法

2.1 状态估计

记pAB=pB-pA表示AUV A、AUV B 间的相对位置，其一阶导数为=vAB，设pABlc表示主、从AUV在时刻的最新一次相对位置数据传输，则协同导航系统的状态方程可以写为

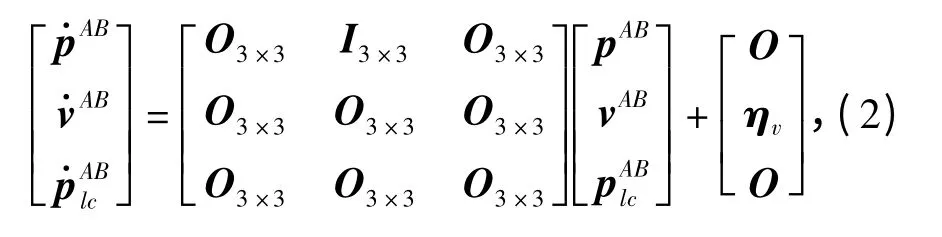
式中，ηv是具有零均值的高斯白噪声，var ηv=diag设系统的状态更新时间为Ttu，则与(2)式相对应的离散时间状态方程为(“-”表示先验估计)

式中，系统噪声

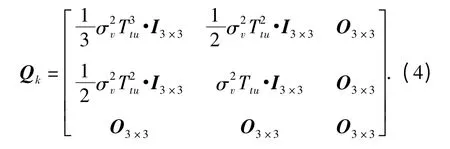
2.2 量测方程与方差更新

主AUV A 可近似连续地获得自身的航位推算定位信息，并经由水声通讯周期性地获取从AUV B的航位推算位置。由于漂移误差的存在，上述航位推算结果的定位误差将随时间的推移持续增长，其增长特性服从高斯白噪声过程［10］

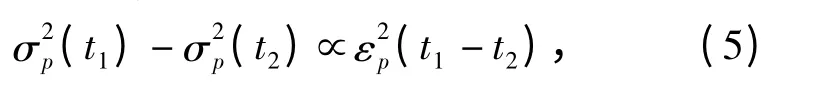
利用连续相邻时刻主、从AUV 的相对位移信息，可以建立系统的位移差量测方程

结合误差模型(5)可得(6)式的量测误差分布

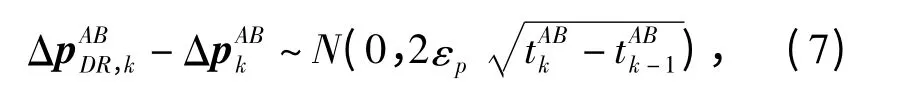
相应的位移差量测矩阵为

位移差量测噪声矩阵为

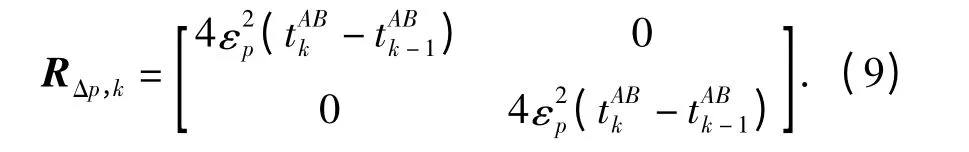
此外，主、从AUV 间的相对速度量测矩阵为

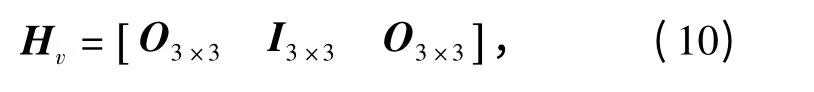
速度量测噪声矩阵为

式中，σ2hz，σ2vt分别表示水平与垂直方向的测速误差。

下面讨论滤波方差的更新。由于状态向量中已经包含了主、从AUV 在tABk时刻的最新一次相对位置数据传输pABlc，因此结合位移差量测方程的构造形式可知，此时滤波方差的更新过程具有比经典的EKF 算法中更为简洁的形式。设Pk(-)表示k 时刻滤波方差的先验估计，ΔpABk为k 时刻新获得的位移差量测值，则滤波方差的更新可以分为两步(“+”表示后验估计):

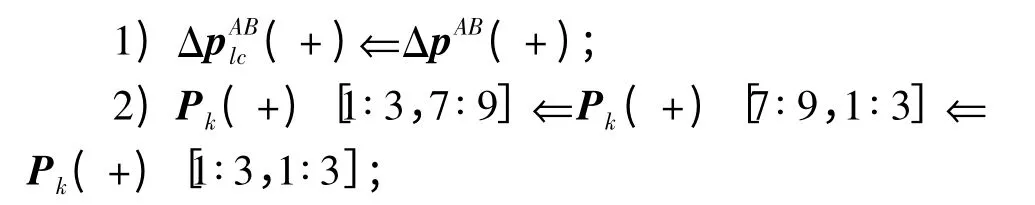
其中方括号部分表示与Pk(+)中相对应的子矩阵。

2.3 量测数据的选取

考虑到水下通讯环境的复杂性，在相对位置量测数据被用于滤波之前，应舍弃部分错误的量测值以确保Kalman 滤波器具有较快的收敛性。为此，可以利用先验方差矩阵Pk(-)来判断tABk时刻所获得的pAB(tABk)是否为一“好”的量测值。Pk(-)的主对角项描述了状态变量估计误差的方差。对于状态向量s(tABk)=［(pAB(tABk))T(vAB(tABk))T主对角线的前两项分别是主、从AUV 的相对位置坐标ΔxAkB，ΔyAkB估计误差的方差σ2Δx(tAkB)，σ2Δy(tAkB).由此，可以定义一个描述时刻相对位置估计不确定性的圆域，其半径为

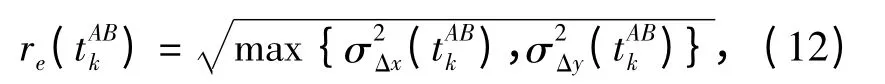
此时，如果量测值pAB(tABk)满足

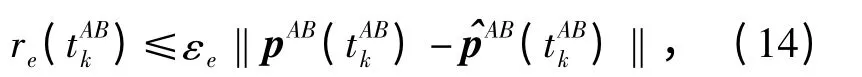
则认为pAB(tABk)是有效数据，否则应当予以舍弃。(14)式中的εe是可以根据不同的实际情况加以适当选取的正常数。判据(14)式可作为EKF 导航算法中的一个子模块加以使用。

3 可观测性分析

可观测性作为动态系统的重要性质之一，描述了系统的状态量能否经由量测数据加以求解。由前述讨论可知，当主、从AUV 以相同的速度沿同一方向平行航行时，协同导航系统全局不可观测。本节进一步研究单领航者协同导航系统的局部可观测性，这在实际应用中更具有普遍意义［11］(在大多数情形下，系统的全局可观测性条件是难以获得的)。

定义tAkB时刻关于相对位置量测量rAB，ΔpAB的向量函数

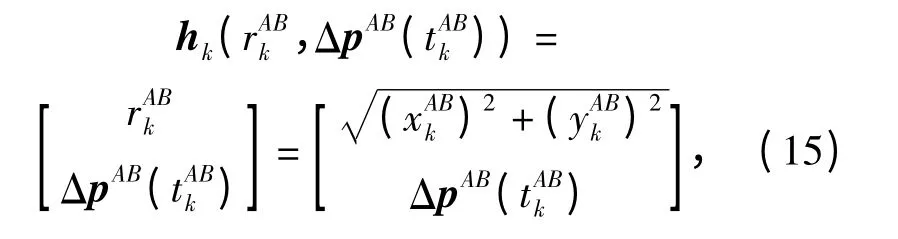
经过一个采样周期Ttu=tk+1-tk，并结合(15)式可得

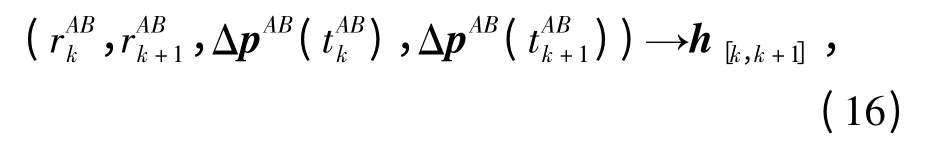
即

直接计算映射(16)式的Jacobi 行列式可得

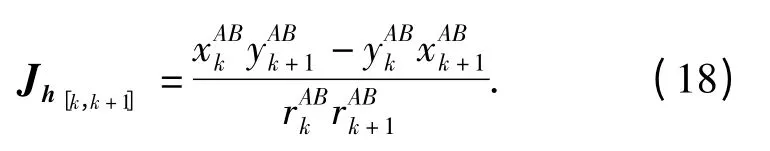
因此，协同导航系统局部可观测的条件是Jh［k，k+1］≠0，即

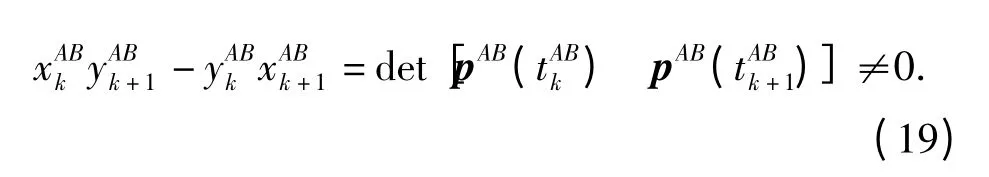
分析(19)式知，如果导航系统局部可观测，当且仅当相邻的两个相对位置量测值pAB(tABk)和pAB(tABk+1)线性独立。利用(19)式可以方便地检测系统的局部可观测性:设δ0是一给定的正常数，pAB(tAkB)，pAB(tAkB+1)是相邻的两个量测值，如果

则系统不可观测或近似不可观测，此时需要调整主、从AUV 的运动轨迹以保持系统的可观测性，并以此保证定位解算的正确性。

4 仿真结果

为检验文中协同导航算法的有效性和实用性，进行仿真分析研究。如图2所示，AUV1(领航者)由坐标原点出发沿直线航行，AUV2、AUV3 首先按斜线航行一段距离，然后与AUV1 保持平行航行。AUV1 的航速为2 m/s，AUV2 和AUV3 的航速为1 m/s，传感器采样周期为1 s.速度信息由多普勒速度传感器测量，取σ2v=(0.1 m/s)2的零均值高斯白噪声;航向角信息由陀螺罗经测量，取σ2φ=(0.5°)2的零均值高斯白噪声;AUV 间的相对位置量测噪声取σ2r=(0.1 m)2的零均值高斯白噪声。

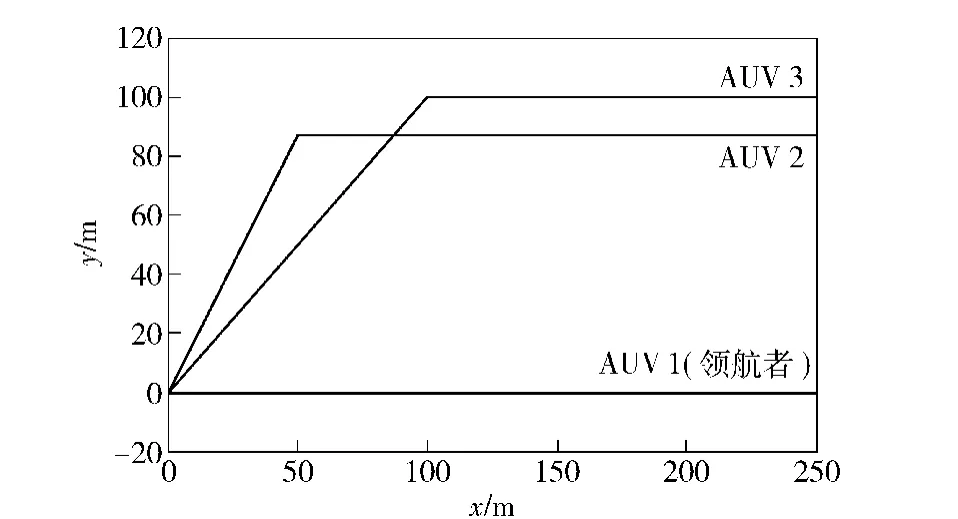
图2 AUV 的仿真运动路径Fig.2 The simulated trajectories of AUVs

图3给出了从AUV 的EKF 协同导航算法轨迹。由图3可知，EKF 协同导航算法轨迹与真实轨迹(见图2)有较好的吻合性，且在全航程中保持稳定。图4分别给出了AUV2、AUV3 的协同导航定位误差。可以看到，在整个航程中，AUV2、AUV3 的定位误差中值约为2.5 m，单一方向的最大定位误差不超过5 m，具有较高的导航定位精度。

为进一步检验文中导航算法的性能，将文献［7］中的CN 导航算法、文献［9］中的LM-EKF 导航算法与文中方法进行比较(见表1)，三种算法的仿真均采用图2所示的运动路径和本节所给定的初始条件。

图3 从AUV 的协同导航轨迹Fig.3 Cooperative navigation trajectories of follower AUVs

图4 从AUV 的定位估计误差Fig.4 Localization errors of follower AUVs

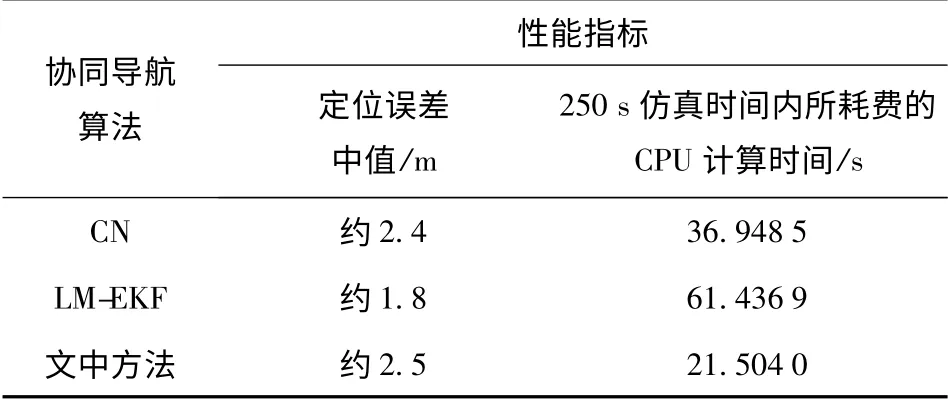
表1 三种协同导航算法的性能比较Tab.1 Performance comparison of three cooperative navigation algorithms

由表1可以看出，在相同仿真时间内，文中的导航算法实现了与CN 算法相当的导航定位精度，但所耗费的CPU 计算时间仅为后者的58%.LM-EKF方法首先采用LM 算法优化了EKF 滤波器的初值，因而其定位精度有所提高。但是，LM-EKF 方法所耗费的CPU 计算时间大约是文中方法的2.86 倍，可见其在提高定位精度的同时牺牲了部分导航解算的实时性。相比而言，文中的导航算法较好地兼顾了定位精度与实时性两方面的要求，在不太损失定位精度的同时有效提高了计算效率。

5 结论

结合单领航者AUV 协同导航系统的定位原理和运动学模型，基于相对位移测量、航位推算信息及相邻时刻主、从AUV 间相对位置的几何关系，提出了一种多AUV 协同导航算法。仿真结果表明，基于EKF 的协同导航算法具有较高的定位精度，且与文献［7，9］中的导航算法相比，有效提高了定位解算的实时性。

References)

［1］ Kinsey J，Eustice R，Whitcomb L.A survey of underwater vehicle navigation:recent advances and new challenges［C］.The 7th IFAC Conference on Maneuvering and Control of Marine Craft，Lisbon，Portugal，2006:1-12.

［2］ Eustice R，Whitcomb L，Singh H，et al.Recent advances in synchronous-clock one-way-travel-time acoustic navigation ［C］.Oceans'06 MTS/IEEE Conference on Exhibition，Boston，USA，2006，1-7.

［3］ Stutters L，Liu H，Tiltman C，et al.Navigation technologies for autonomous underwater vehicles［J］.IEEE Transactions on Systems，2008，38(4):581-589.

［4］ Chandrasekhar V，Winston S，Yoo S C，et al.Localization in underwater sensor networks-survey and challenges［C］.Proceedings of the 1st ACM International Workshop on Underwater Networks，New York，2006:33-40.

［5］ Bahr A，Leonard J，Fallon M.Cooperative localization for autonomous underwater vehicles［J］.The International Journal of Robotics Research，2009，28(6):714-728.

［6］ Baccou P，Jouvencel B，Creuze V，et al.Cooperative positioning and navigation for multiple AUV operations［C］.Oceans'01 MTS/IEEE Conference and Exhibition，Honolulu，2001:1816-1821.

［7］ Bahr A.Cooperative localization for autonomous underwater vehicles［D］.Massachusetts Institute of Technology and Woods Hole Oceanographic Institution，2009.

［8］ Gadre A.Observability analysis in navigation systems with an underwater vehicle application［D］.Virginia Polytechnic Institute and State University，2007.

［9］ Baccou P，Jouvencel B.Simulation results，post-processing experimentation and comparison results for navigation，homing and multiple vehicle operations with a new positioning method using a transponder［C］.Proceedings of the 2003 IEEE/RSJ International Conference on Intelligent Robotics and Systems，Las Vegas，2003:811-817.

［10］ 秦永元，张洪钺，汪叔华.卡尔曼滤波与组合导航原理［M］.西安:西北工业大学出版社，2007.QIN Yong-yuan，ZHANG Hong-yue，WANG Shu-hua.Kalman filter and integrated navigation principles［M］.Xi'an:Northwestern Polytechnical University Press，2007.(in Chinese)

［11］ 郑大钟.线性系统理论［M］.第2 版.北京:清华大学出版社，2002.ZHENG Da-zhong.Linear system theory［M］.2nd ed.Beijing:Tsinghua University Press，2002.(in Chinese)