定时截尾试验中故障数为零装备的平均无故障间隔时间评估方法研究

郭荣化，吴玉生，陈庆荣

(中国华阴兵器试验中心，陕西 华阴714200)

0 引言

定时截尾可靠性试验，就是当试验进行到预定的试验时间t 时，就终止试验，然后根据试验中被试装备发生的故障个数，对装备作出“接收”或“拒收”的判定，同时对装备的可靠性作出评估。由于定时截尾试验具有很强的计划性和可操作性，是目前可靠性工作者最乐意选择的使用方法。

但随着武器装备设计不断优化，元器件水平逐步提高，在定时截尾可靠性试验中，当试验结束时，出现零个关联故障的概率也在逐渐地提高。针对这种情况如何做出正确的试验结论，目前在国标、国军标的资料中，都未有明确提出具体的实施意见。

1 相关评估标准缺陷

《GJB899—90 可靠性鉴定和验收试验》中(A-8)式，给出了基于指数分布的极大似然估计法推导而来的平均无故障间隔时间(MTBF)观测值点估计^θ 的计算方法

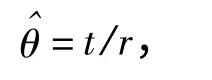
式中:t 为设备的总试验时间;r 为责任故障。

同时在(A-11)式给出了定时截尾试验中接收时MTBF 的置信下限系数θl公式和置信上限系数θu的计算方法

上述公式在无故障发生时均无法应用，因为无故障发生时r 为0，根据点估计评估公式得出MTBF的估计值为无穷大;同样在自由度m 为0 时χ2分布也不存在。

但在GB5080.4—85《设备可靠性试验可靠性测定试验的点估计和区间估计方法(指数分布)》中5.1.1 条规定，在指数分布场合，若到测定点没有观察到失效数据，推荐用下述公式计算失效率^λ

因为产品的平均寿命与产品的故障率互为倒数关系，即可用总试验时间的3 倍作为平均寿命(MTBF)估计。上述规定也只是一个经验的办法，国标中没有给出推导过程和相关依据，取3 倍试验时间作为MTBF 估计值的做法至今也尚未在其他文献和资料查找到充分理论证明。

近年来，统计学家对无失效情况进行了相应研究，如文献［1-2］提出配分布曲线法;文献［3-13］采用Bayes 或多层修正Bayes 法;文献［14］给出了指数分布情况下的修正似然函数法;文献［15-16］采用公式和权系数给出一种类似经验法;文献［17-18］采用再抽样方法，利用Monte-Carlo 方法进行了随机模拟和参数估计;文献［19-20］采用最大期望(EM)算法，并与极大似然估计及修正极大似然估计进行了比较;文献［21］采用信息测度方法建立寿命检验方法等。关于无失效数据的若干研究进展情况，见参考文献［22］。上述诸多研究中，以对Bayes 方法研究居多，而且主要方向为采用分层Bayes 方法以及不同先验分布的情况下各种估计，这些方法理论性较强，侧重于在无失效情况下的数学推导和理论证明，由于各种方法引起估计结果的差别没有统一的判定依据，无法形成在无失效情况下可靠性鉴定试验相应的操作方法，难以在实际可靠性试验中进行实施和评估。此外，文献［23］通过定义最大置信下限和正则置信下限概念，推导出无故障情况下计算最优置信下限的普遍公式，但是由于其推导过程理论性很强，不便于一般工程人员理解和接受。

针对上述问题，本文根据指数分布的累积分布函数性质，利用一次试验中小概率事件是不会发生的原理，进行反证法论证，推导出无故障情况下MTBF 的验证值确定方法，弥补了依据GJB899 中公式无法确定MTBF 验证值的不足。由于本文提供的推导方法避开了较为复杂数学推导，并给出具有较为明确的工程物理背景的各个估计方案，在进行可靠性鉴定试验设计时，通过双方协商，可提前选取合适的参数估计方案，使本文提供的方法具有很强的可操作性和工程应用价值。

2 验证区间推导

可靠性鉴定试验中若产品寿命服从指数分布，产品累积分布函数可表示为

式中:ti为可靠性试验中第i 个故障发生的时间;θ为平均无故障间隔时间MTBF 值。

设从一批产品中取n 个进行定时截尾试验，到规定的时间并未发现产品故障，产品的工作时间为

假定题设样本E 的发生概率为P(E)时，则有下式成立

式中，tΣ为到规定的截止时间所累积的相关试验时间。

通过(2)式可知，若θ 减小时，P(E)随之减小，即P(E)随θ 具有单调递减性。假设MTBF 下限值θl是已知，在产品的MTBF 设计值是合理的基础上，那么θ 应以一个较大的概率大于MTBF 下限值θl，即MTBF 下限θl大于θ 的概率是个小概率，根据P(E)的单调性，如果存在θ≤θl，则发生P(El)事件的概率也必为一个小概率α 事件

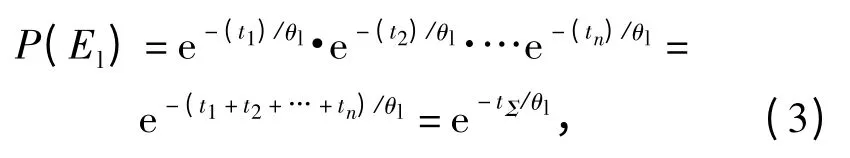
即有

所以满足上式的MTBF 置信下限θl计算公式为

上述公式结果，与文献［23］推导出来的指数分布下零故障最优置信下限可靠性评估公式使一致的，其区别在于文献［23］在θ 已知情况，假设θl是变化的，然后推导出最优的θl;本文假设θl已知，在θ减少至θl后，试验中出现无故障发生的事件将是一个小概率事件，从而获得置信下限θl计算公式。虽然推导过程不一样，但是公式意义都是一样的，文献［23］定义正则性的一个物理意义可以简要表述为:无故障情况下置信下限不会小于有故障情况下的置信下限。本文的小概率推导过程中一个物理意义可简要表述为:产品MTBF 取在置信下限情况下无故障发生的概率小于区间估计中任何一个MTBF值时的无故障发生概率。

3 点估计方案

在前节验证区间的推导中，得到了MTBF 的验证下限，根据(5)式控制置信水平变动，在某一风险范围附近，存在一个置信水平α'的θ'l等于MTBF 的值，故此，我们可以将此时的估计下限作为MTBF 的点估计，即得到下式

由上述推导的(6)式，可以计算在不同置信度α'下，MTBF 的这个置信下限θ'l值，即^θ 关于总试验时间tΣ的倍数关系，这个关系可以用来获得合理的MTBF 点估计，获得的计算方案见表1.

表1 无故障发生时MTBF 点估计计算方案简表Tab.1 The calculation scheme of the point estimation of MTBF of zero-failure

上述计算方案主要是在产品寿命服从指数分布情况下，解决在采用定时截尾试验中无故障发生时进行MTBF 真值估计问题，弥补在试验中接收的判决故障数位零发生时MTBF 无法估计的难题。上述计算方案理论上可以适用于包括GJB899—90《可靠性鉴定和验收试验》中给出的标准定时截尾试验1～17 号方案和短时高风险19～21 号方案，尤其适用于接收的判决故障数较少的方案中，比如GJB899的标准定时截尾试验方案17，短时高风险方案20和方案21，因为这些方案接收的判决故障数分别为2/2/0，在实际试验过程中无故障情况的出现概率也较高。

表1提供的无故障发生时MTBF 点估计计算方案简表给出了在定时截尾试验中，零故障时的MTBF 点估计值和置信度之间的关系，选取不同的置信度将会得到不同的MTBF 估计值，其中置信度选取主要依据产品本身的技术状态。下面针对不同工程应用环境对各个方案的选取进行说明。

如果进行可靠性鉴定试验的武器装备采用较多高新技术，作战使用中需要极高的可靠性，或者定时截尾试验选用的短时高风险、鉴别比又较大的试验方案，在进行MTBF 的点估计的计算时，订购方可以选择风险更小的保守方案1、2、3，让生产方承担较大的风险。其中，方案2 计算MTBF 点估计值结果等于r 为1 时的MTBF 估计值，即认为如果继续进行可靠性试验，会立即出现1 个故障。

如果进行可靠性鉴定试验的武器装备属于成熟产品，或者基于可靠性鉴定试验前的数据有理由相信武器装备的可靠性较高，可以选择方案5、6、7 等。其中方案7 与GB5080.4—85 推荐的计算结果是一致的，此方案订购方承担风险要高于生产方。

例如，某新型电子侦察装备，选用GJB899 标准定时试验方案中17 号方案(双方名义风险均为20%，判决故障的接收数Ac≤2，判决故障的拒收数Rc≥3)进行可靠性鉴定试验，试验结束后没有出现故障，总试验时间t=24(台时)，该如何给出试验结果?

因为产品试验过程中零个故障，根据17 号方案试验结束后故障数小于3 个，可以做出接收产品为合格的判定，在对其进行MTBF 估值时，采用GJB899 提供的公式=t/r 将无法计算，因考虑其作战过程中任务可靠较高，又为新型电子侦察装备，其以前可靠性水平掌握较少，故可选取文中表1提供较为保守的3 号方案，MTBF 的估计值计算结果为28.8 h.

4 结论

在可靠性鉴定试验中，产品在有故障下的数据处理已有一套成熟的方法，但是对无故障情况下的处理还处于研究探讨阶段，常用的极大似然估计法也随之失效，本文经过推导和分析解决了下述两个问题:

1)获得了无故障时可靠性鉴定试验中的MTBF置信下限公式。

2)提供了无故障情况下，MTBF 的点估计计算方法，并给出了几种典型的方案和应用环境分析。

本文研究的内容对GJB899 中在无故障发生时MTBF 的验证值难以确定作了较好的补充，根据可靠性试验方案设计，在可靠性试验进行前可以根据产品技术状态和工程背景，双方协商选取文中提供的某一方案，以此确定如果在可靠性试验中无故障时的MTBF 验证值计算方法，避免了在试验完成后对MTBF 估计可能产生的分歧，本文研究的内容和提供的方案对可靠性鉴定试验具有很强的指导性和可操作性，具备很强的工程应用和推广价值。

References)

［1］ 茆诗松，罗朝斌.无失效数据的可靠性分析［J］.应用概率统计，1990，4(4):489-506.MAO Shi-song，LUO Chao-bin.Reliability analysis for zero-failure data［J］.Chinese Journal of Applied Probability and Statistics，1990，4(4):489-506.(in Chinese)

［2］ 王伟，夏新涛.配分布曲线法在无失效数据可靠性分析中的应用［J］.轴承，2006，(3):20-22.WANG Wei，XIA Xin-tao.With distribution curves in the zero-faliure data reliability analysis［J］.Bearing，2006，(3):20-22.(in Chinese)

［3］ 韩明.多层先验分布的构造及其应用［J］.运筹与管理，1997，6(3):31-40.HAN Ming.The hierarchical prior-distribution structure and its application［J］.Operations Research and Management Science，1997，6(3):31-40.(in Chinese)

［4］ 王建华，袁力.无失效数据下失效概率的多层Bayes 和EBayes 估计的性质［J］.工程数学学报，2010，(1):78-84.WANG Jian-hua，YUAN Li.The properties of failure probability of hierarchical prior-distribution and the E-Bayes estimation Bayes of zero-failure［J］.Chinese Journal of Engineering Mathematics，2010，(1):78-84.(in Chinese)

［5］ 孙少葆.指数分布无失效数据的Bayes 估计［J］.长春理工大学学报:高教版，2008，(1):168-172.SUN Shao-bao.The bayes estimation of zero-failure based on exponential distribution［J］.Journal of Changchun University of Science and Technology:Social Sciences，2008，(1):168-172.(in Chinese)

［6］ 余文波，任海平.成败型试验中无失效数据的多层Bayes 分析［J］.南昌大学学报:理科版，2009，(2):130-132.YU Wen-bo，REN Hai-ping.The hierarchical bayes analysis based on the success-failure type of zero-failure［J］.Journal of Nanchang University:Natural Science，2009，(2):130-132.(in Chinese)

［7］ 张晓冉，张海娟，高作峰.无失效数据的一类迭代Bayes 分析［J］.武汉大学学报:理学版，2009，(4):399-404.ZHANG Xiao-ran，ZHANG Hai-juan，GAO Zuo-feng.An iterative bayes analysis of zero-failure［J］.Journal of Wuhan University:Natural Science，2009，(4):399-404.(in Chinese)

［8］ 李亿民.关于指数分布无失效数据的一种Bayes 分析［J］.山东理工大学学报:自然科学版，2006，(2):17-19.LI Yi-min.A Bayesian analysis for non-failure data of exponential distribution［J］.Journal of Shandong University of Technology:Science and Technology，2006，(2):17-19.(in Chinese)

［9］ 韩明.无失效数据情形可靠性参数的估计和调整［J］.应用数学，2006，19(2):325-330.HAN Ming.Estimation and rectification of reliability parameters in the case of zero-failure data［J］.Mathematica Applicata，2006，19(2):325-330.(in Chinese)

［10］ 韩明.无失效数据的多层Bayes 可靠性分析［J］.应用数学，1998，(2):131-134.HAN Ming.The hierarchical bayesian reliability analysis of zerofailure data ［J］.Mathematica Applicata，1998，(2):131-134.(in Chinese)

［11］ 曲贺梅，高风昕，党平安.电器无失效数据的Bayes 可靠性分析［J］.数学的实践与认识，2008，(13):144-147.QU He-mei，GAO Feng-xin，DANG Ping-an.Bayes reliability analysis of electrical appliances zero-failure data［J］.Mathematics in Practice and Theory，2008，(13):144-147.(in Chinese)

［12］ Coolen F，Coolen-Schrijner P.On zero-failure testing for Bayesian high-reliability demonstration［J］.Proceedings of the Institution of Mechanical Engineers，Part O:Journal of Risk and Reliability，2006，220(1):35-44.

［13］ Bailey R T.Estimation from zero-failure data［J］.Risk Analysis，2006，17(3):375-380.

［14］ 王玲玲，王炳兴.无失效数据的统计分析:修正似然函数方法［J］.应用概率统计，1996，11(1):64-70.WANG Ling-ling，WANG Bing-xing.The statistical analysis of zero-failure data:modified likelihood function approach［J］.Chinese Journal of Application Probability and Statistics，1996，11(1):64-70.(in Chinese)

［15］ 刘伟，袁新，乔明锋.定时截尾试验中故障数为零的设备MTBF评估［J］.电子产品可靠性与环境试验，2007，25(1):19-21.LIU Wei，YUAN Xin，QIAO Ming-feng.The estimation method of MTBF for zero-failure data in reliability time truncated qualification test［J］.Electronics Product Reliability and Environmental Testing，2007，25(1):19-21.(in Chinese)

［16］ Huang Z L，Yu F X，Zhang S T.Empirical-statistics analysis for zero-failure GaAs MMICs life testing data［J］.IEICE TRANSACTIONS on Fundamentals of Electronics，Communications and Computer Sciences，2009，92(9):2376-2379.

［17］ 张琼，李凡群.Bootstrap 方法在无失效数据分析中的应用［J］.安庆师范学院学报:自然科学版，2006，(3):26-28.ZHANG Qiong，LI Fan-qun.The application of bootstrap methods in the data-analysis of zero-failure［J］.Journal of Anqing Teachers College:Natural Science，2006，(3):26- 28.(in Chinese)

［18］ 樊磊.基于自助法的无失效小样本可靠性评估［J］.微计算机信息，2008，24(33):209-211.FAN Lei.The reliability assessment of small samples based on bootstrap methods of zero-failure［J］.Control ＆ Automaion，2008，24(33):209-211.(in Chinese)

［19］ 纪志荣，黄可明.基于EM 算法的无失效数据的参数估计［J］.福州大学学报:自然科学版，2007，(4):507-510.JI Zhi-rong，HUANG Ke-ming.The parameter estimation of zerofailure based on EM algorithm［J］.Journal of Fuzhou University:Natural Science，2007，(4):507-510.(in Chinese)

［20］ 赵海兵，程依明.无失效数据的EM 算法［J］.华东师范大学学报:自然科学版，2006，(5):93-98.ZHAO Hai-bing，CHENG Yi-ming.The EM algorithm of zerofailure［J］.Journal of East China Normal University:Natural Science，2006，(5):93-98.(in Chinese)

［21］ 吴绍敏.以熵为测度的无失效抽样检验法［J］.华侨大学学报:自然科学版，2001，(2):128-132.WU Shao-min.The sample test of zero-failure based on entropy measure［J］.Journal of Huaqiao University:Natural Science，2001，(2):128-132.(in Chinese)

［22］ 韩明.无失效数据可靠性进展［J］.数学进展，2002，(1):7-19.HAN Ming.The progress in the zero-failure reliability study［J］.Advances Mathematics，2002，(1):7-19.(in Chinese)

［23］ 陈家鼎，孙万龙，李补喜.关于无失效数据情形下的置信限［J］.应用数学学报，1995，(18):90-100.CHEN Jia-ding，SUN Wan-long，LI Bu-xi.Confidence limits in the case of zero-failure data［J］.Acta Mathematicae Applicatae Sinica，2002，(1):7-19.(in Chinese)