陀螺稳定平台的滑膜变结构控制实验研究

姚兆，刘杰，李允公，衣英刚，高飞

(1.东北大学 机械工程与自动化学院，辽宁 沈阳110004;2.装甲兵技术学院，吉林 长春130117)

0 引言

陀螺稳定光学探测平台作为一种高精度的视轴稳定系统，可以实现对地、对空目标的全景式大范围探测和跟踪。它既可作为独立的光电观瞄系统用于侦察任务，也可作为火控系统的组成部分完成战场作战任务。其主要功能是隔离载体角运动，使探测器在惯性空间内保持稳定;它也能够响应指令信号，在一定角度范围内对目标进行搜索，在人工识别锁定后能够按探测器信号自动跟踪目标，并给出方位、俯仰等角度信息，其实质就是一种速度伺服控制系统。目前，针对视轴稳定控制提出了许多控制方法，文献［1-2］提出了采用高斯型RBF 神经网络对摩擦力矩进行观测和补偿的方法，同其他方法相比具有较好的自适应能力和较高的精度;对于机械谐振的克服，除了采用陷波滤波器外，文献［3］提出了采用简单的FIR 滤波器方法，并通过实验验证了其效果;文献［4-5］分析了陀螺噪声对稳定精度的影响，提出了采用Kalman 滤波器预测实际角速率方法，仿真结果表明该方法在低信噪比情况下有效地估计了实际的角速率输出;文献［6］针对稳定系统中的非线性扰动，采用LQG 和Kalman 滤波算法对扰动进行实时估计和补偿，并采用自校正控制的方法以提高LQG 算法的鲁棒性，实验结果表明，这种方法同采用传统的PI 和陷波器方法相比，精度提高了近一倍，但这些方法由于计算过于复杂或者过于依赖控制对象的精确数学模型，仅适合仿真，难于实现。在工程实践中，由于系统存在各种非线性扰动因素，采用常用的PID 控制或PD 控制作为速度控制器，很难保证稳定平台的扰动隔离精度，尤其是在低速运行时，常常出现速度的死区现象和非平稳现象，如文献［7］采用的H∞控制和文献［8］采用的模糊控制方法等，很难在实际系统中应用。本文以某型号火控系统稳定平台为实际背景，在分析双轴稳定平台结构和惯性稳定原理的基础上，根据系统非线性、不确定特性以及特殊应用环境，提出采用滑膜变结构控制策略，并进行了实验验证。实践证明，该系统具有负载特性好，响应速度快、稳定精度高、抗冲击力强等特点，有效地提高了系统的扰动隔离精度和鲁棒性，同时，系统结构简单，体积小，质量轻，具备很强的实用性。

1 稳定平台系统结构

该稳定平台主要由双轴速率积分陀螺仪、方位向和高低向直流力矩电机、方位向和高低向解算器、1/2 钢带传动机构、支撑框架、电磁锁定装置及轻质反射镜等构成。力矩电机为有限角直流力矩电机，安装于上反头部机械转动框架上，两台电机分别提供高低轴和方位轴输出力矩。双轴速率积分陀螺采用挠性陀螺，安装于平台框架上，它是稳定平台的核心部件，用于敏感台体的扰动速率和反射镜转动的角度。其输出信号通过线性变化、变系数等处理，与稳定伺服校正电路、功率放大电路和力矩电机构成稳定、伺服控制系统，实现反射镜对大地空间的稳定。图1为稳定平台原理框图。

图1 稳定平台原理框图Fig.1 Block diagram of stabilized platform

2 稳定平台总体设计

采用三维结构造型分析软件，分析稳定平台机械构造、传动结构特点和负载特性参数，决定关重传感器件的性能参数。根据仿真计算出的负载特性和系统总体对稳瞄控制系统性能指标的要求，对上反组件内安装的陀螺、电机和角度传感器等关重件进行选型，对控制系统建模，通过仿真计算确定电路参数。同时，为了提高建模的准确性，采用先进的三维造型软件精确仿真计算上反射镜的负载特性，根据系统总体指标要求和所选传感器特性参数，在系统建模时采用Matlib ＆ Simulink 系统设计与分析软件，考虑各种参数扰动影响，进行模型分析与数字动态仿真，反复验证模型的准确性。考虑到稳瞄控制系统是一个高精度控制系统，陀螺、旋转变压器等器件的输出信息属于微弱信号，极易受到电磁干扰，影响到系统的稳定精度或同步精度，另外系统控制电路中还存在大功率电流和高频脉冲，会对稳瞄控制系统造成影响。为此，对系统和电路中所有弱信号和大电流、高频脉冲信号都做了屏蔽保护，电路接地采用了分类分级接地和单点接外壳方式，滤波电路还采用了金属屏蔽方式，以尽量减少干扰［9］。

控制模块采用集成DC/DC 电源模块分区统一供电，电源精度高、可靠性好、稳定性好;功率放大电路采用电流反馈保护方式，并实行一体化散热，提高整个系统可靠性。系统的位置伺服控制采用数字控制方式实现位置传感器信号采集处理和位置校正。

3 滑模变结构控制器设计

陀螺瞄准线稳定系统除了具有运动控制中常见的机械谐振、电机死区和极限环振荡，摩擦力矩耦合负载变化以及电气参数波动等问题外，挠性陀螺自身由于扭杆的弹性刚度，信号器与力矩器的稳定与温度等有关，故挠性陀螺存在零位温度漂移现象;陀螺内部的电子器件会产生热噪声，陀螺外部的模拟信号的波动、电源干扰和电磁干扰会导致随机噪声;信号在传输、测量和转换过程中可能引入噪声，大量量测噪声的存在会使辨识的模型具有较高的阶次而无法逼近实际的系统，将会降低控制系统的精度和分辨率，而且，此类光电跟踪系统反应时间很短，稳定控制响应时间一般在毫秒级，因此要求控制系统具有快速动态响应［10］、高质量稳态精度以及对于模型参数变化的自适应能力和鲁棒性。因而常规PID控制器很难达到理想的控制效果。

变结构控制系统是一种特殊的非线性反馈控制系统，是解决有界不可测扰动、系统变参数和模型不确定问题的有效方法。由于滑动模态可以进行设计且与对象参数及扰动无关，使得滑模变结构控制具有快速响应、对参数变化及扰动不灵敏、无需系统在线辨识、物理实现简单等优点。将其应用到稳定平台系统中，可很好的解决精度与快速性之间的矛盾［11］，增强系统鲁棒性，抑制干扰力矩对电机的影响，而且算法较简单，工程上易于实现［12］。引入滑模变结构控制后系统模型如图2所示。

其中:VSC 为滑膜变结构控制器;KG为陀螺的静态传递系数;τG为陀螺的时间常数;RM为电机电枢回路总电阻值;TL为力矩电机的电气时间常数;KM为力矩系数;MT为外界干扰力矩;MF为力矩电机输出力矩;Js为折算到电机轴上的总转动惯量;θo(k 为摇摆引起的视轴偏差修正角);θp(k 为视轴稳定伺服系统输出角度)。

直接针对离散系统的滑模变结构控制，可以不直接考虑采样周期的长度，因为它是一种准滑模控制，原理上又有避免高频抖振的可能;建立在差分方程基础上的离散系统，其状态可由输出、控制等值计算出来，不需要建立观测器，从而使直接针对离散系统的滑模变结构控制，更具有实用性。

1)离散系统滑模区的可达条件

以离散李雅普诺夫稳定性为基础，可推导出离散系统滑模区的可达条件

当采样周期T 很小时，其等价的两个不等式是

(2)式是保证状态轨迹进入滑模区s(k)=0 的必要条件，称为滑模必要条件;而(3)式保证状态轨迹收敛到s(k)=0，称为滑模收敛条件。

2)基于趋近律的离散滑模控制器设计

基于趋近律的控制器设计是滑模变结构控制的一种典型控制策略，这种控制方法不仅可以对系统在切换面附近或沿切换面的滑模运动段进行分析，而且可以有效的对系统趋近段的动态过程进行分析和设计，从而保证系统在整个状态空间内具有良好的运动品质。

在连续控制系统中，常用的趋近律为指数趋近律

对于离散系统可将(4)式离散化，即得离散指数趋近律为

式中，ε ＞0，q ＞0，1-qTs＞0，Ts为采样周期。

由上式不难证明滑模区的可达条件成立，如下

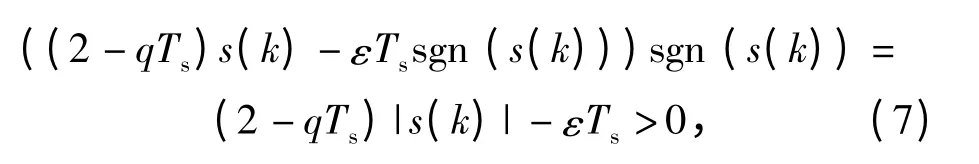
即离散指数趋近律(5)式满足滑模区的可达条件。

针对离散系统

离散滑模面为

将s(k+1)=Cx(k+1)=CAx(k)+CBu(k)代入趋近律(5)式得

得到离散滑模控制律为

忽略电机电气时间常数的影响，本系统的开环传递函数为

其离散状态空间表达式为

取R(k)=［θ0(k);+dθ0(k);d2θ0(k)］，R(k+1)=［θ0(k+1);+dθ0(k+1);d2θ0(k+1)］

切换函数可写为

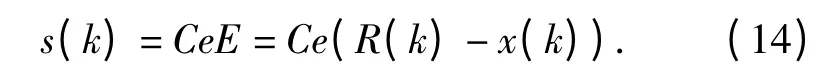
其中Ce=［C1，C2，1］，则

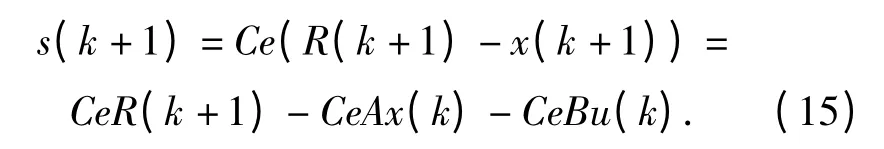
控制规律为

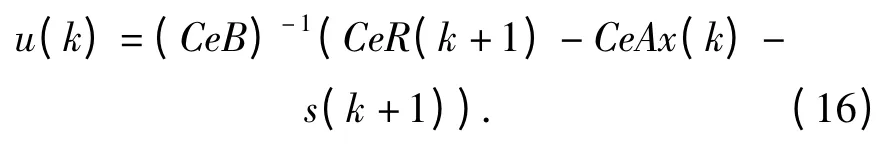
将s(k+1)-s(k)=-qTss(k)-εTssgn (s(k))代入，得

其中c1，c2，q，ε 为可变参数。滑模参数c1和c2对系统调节时间有较大的影响。趋近速度参数q 主要影响切换函数的动态切换过程，适当调整该参数能够改变系统向滑模面的趋近速度，可以更好的改善系统动态性能。符号函数增益参数ε 代表了系统克服摄动及外干扰的能力［13］。经过试验，c1，c2，q，ε 分别取值为35、40、30、20，此时系统具有较小的稳态误差和较高的抗干扰能力。

4 试验及结果分析

对该稳瞄系统分别做了摇摆试验、振动试验和冲击试验。试验时，在主试验台(摇摆台、振动台、冲击台)上面中央位置放置一个平面镜，将稳定平台固定于主试验台上，并使稳定平台底面轴向与平面镜的轴向重合。平行光管用来测量组件内上反射镜的运动情况，光管的目镜内以正中央为原点，上下左右均有一定刻度。接通平行光管电源，使其向正前方发射平行光束，将目镜对准测量组件的上反射镜，则上反射镜将平行光束反射至平面镜;而后光束将沿相同路径返回平行光管的目镜，形成一个十字分划，通过调整目镜在方位和俯仰轴向的位置，可使十字分划与目镜的原点重合。试验中，观察目镜内十字分划的运动轨迹，便可知稳定平台高低向稳定误差α 和方位向稳定误差β 最大值，具体数据如表1～表3所示。

表1 摇摆试验稳定误差Tab.1 Stabilization error of swing test

通过对试验数据进行分析可以得出以下结论:

1)在使用平行光管作静态观察时，瞄线基本保持不动，证明系统对噪声的抑制比较成功，达到了比较理想的动态性能［14］，工作可靠，稳定精度高，达到了平台稳定精度的设计要求。

2)在整个高低角工作范围内，瞄准线沿方位向的振幅，在10～40 Hz 频率范围内，不超过20″，在40～120 Hz 频率范围内，不超过30″.但在40～70 Hz谐振频率点上的振幅达1'，在70～120 Hz 谐振频率点上的振幅达2'，这是由于机械谐振造成的。系统的频带宽度越宽机械谐振对系统动态特性的影响就越显著。所以在机械加工中，应尽量提高系统的机械谐振频率，以使其远离系统的中频带。为抑制机械谐振频率，在对采集到的陀螺数据作放大校正预处理时使用了陷波器，在120 Hz 以下，垂直向和水平向都没有出现严重的超差点，在40 Hz 以内，系统误差均不超过20″，证明系统的低频精度较高。

表2 振动试验稳定误差Tab.2 Stabilization error of vibration test

表3 冲击试验稳定误差Tab.3 Stabilization error of impact test

3)火炮后座对系统精度的影响最为严峻，冲击试验充分证明了这点。冲击过程中，陀螺的输出信号很大，在50 g 峰值加速度下，系统最大动态误差可达5'，但是在冲击过后，瞄准线可基本回归原位，系统达到设计要求。

5 结论

陀螺稳定平台系统中的非线性因素，直接影响到系统的速度闭环控制精度，进而影响到整机的目标跟踪精度和跟踪速度。尤其是对低速性能要求很高的高精度光电跟踪设备，必须采用有效的控制方法消除非线性扰动因素。另外，由于火控系统对稳定平台的精度、抗振动、抗冲击等性能要求较为苛刻，如果采用经典的PID 控制器，只能靠提高力矩刚度来加强对力矩干扰的抑制程度，但同时也将带来稳定性问题。本文利用滑模变结构控制方法对模型参数变化、非线性和外扰噪声的不敏感性，设计的稳定平台系统无超调，响应速度快而且抗干扰能力强，具有很好的鲁棒性。实验表明，该方法可以有效地消除系统中的非线性扰动，改善陀螺速度闭环的低速性能，视轴稳定精度因此提高了50%以上，同时在控制中有效地避免了滑模抖振现象，可靠性高。

References)

［1］ Du H L，Satish S.N.Modeling and compensation of low-velocity friction with bounds ［J］.IEEE Transation on Control Systems Technology，1999，7(1):110-121.

［2］ Jayesh A.Implementation of a friction estimation and compensation technique［J］.IEEE Control Systems，1997，8:71-76.

［3］ Slobodan N.Vukosavic.Suppression of torsional oscillations in a high-performance speed servo drive［J］.IEEE Transation on Industry Electronics，1998，45(1):108-117.

［4］ Marcelo C A，Douglas E E.Novel kalman filtering method for the suppression of gyroscope noise effects in pointing and tracking systems［J］.Optical engineering，1995，34(10):3016-3030.

［5］ Marcelo C A.Kalman Filtering Approach for Reducing Gyroscope Noise Effects in Stabilized Platforms［C］∥SPIE Conference on Acquisition，Tracking，and Pointing VI，Albuquerque:1992，1697:399-413.

［6］ Li B ，Hullender D ，DeRenzo M .Nonlinear induced disturbance rejection in inertial stabilization systems［J］.IEEE Transation on Control System Technology，1998，6(3):421-427.

［7］ Shen J C.H∞control and sliding mode control of magnetic levitation system［J］.Asian J Control，2002，4(3):333-340.

［8］ Chen B，Liu X P.Fuzzy approximate disturbance decoupling ofMIMO nonlinear systems by backstepping and application to chemical processes ［J］.IEEE Transactions on Fuzzy Systems，2005，13(6):832-847.

［9］ 帐德宁.上反稳瞄系统数字化控制研究［D］.天津:天津大学，2006.ZHANG De-ning.Research on digital control of upper reflector aim-stabilization system［D］.Tianjin:Tianjin University，2006.(in Chinese)

［10］ Rtega J J.Gunfire performance of stabilized electro-optical sights［C］∥SPIE Conf，Orlando:1999，3692:74-83.

［11］ 李汉舟，刘修彦.挠性捷联惯性导航系统误差补偿技术［J］.中国惯性技术学报，2007，15(4):403-411.LI Han-zhou，LIU Xiu-yan.Error compensation technique for SINS with dynamically tuned gyroscope［J］.Journal of Chinese Ineatial Technology，2007，15(4):403-411.(in Chinese)

［12］ 郭贵莲，盛光忠，崔志强.基于DSP 的全数字滑模变结构直流伺服系统［J］.三峡大学学报:自然科学版，25(5):437-439.GUO Gui-lian，SHENG Guang-zhong，CUI Zhi-qiang.Full-digital SM VSC DC servo system based on DSP［J］.Journal of China Three Gorges University:Natural Science Edition，25(5):437-439.(in Chinese)

［13］ 姚琼荟，黄继起，吴汉松.变结构控制系统［M］.重庆:重庆大学出版社，1997:1-12.YAO Qiong-hui，HUANG Ji-qi，WU Han-song.VSC control system［M］.Chongqing:Press of Chongqing University，1997:1-12.(in Chinese)

［14］ 韩永根.角度无静差陀螺稳定光电探测平台设计与实现［J］.光电工程，2008，35(8):1-4.HAN Yong-gen.Design and implementation of a Gyro stabilized platform with zero steady-state angle error［J］.Opto-Electronic Engineering，2008，35(8):1-4.(in Chinese)