泵控缸电液位置伺服系统建模研究

高强，金勇，王力，侯远龙，季丽君

(1.南京理工大学 机械工程学院，江苏 南京210014;2.总装备部工程兵军代局武汉军代室，湖北 武汉430073)

0 引言

泵控缸电液位置伺服系统是通过改变泵的输出功率来控制传送给负载的动力，其具有功率损失小、效率高等特点，然而与所有电液伺服系统一样，泵控缸电液位置伺服存在非线性和时变性，其非线性主要是由液压阀的死区、滞环、库仑摩擦等因素引起的;其时变性主要表现为液压油液体积弹性模量、油液的粘性、系统的阻尼比等随着油压、油温、阀的开口量的变化而变化［1-2］，使得难以对泵控缸电液位置伺服系统进行精确建模。

机理分析建模法是电液伺服系统常用的建模方法，它运用一些已知的定律、定理和原理，如流量连续性方程、力或力矩平衡方程等，来建立电液伺服系统的数学模型。文献［3-4］利用机理分析建模方法，建立了电液伺服系统的动态数学模型。文献［5-7］推导出了电液伺服系统的状态空间方程，并设计了系统的非线性控制器。机理分析建模法的缺点在于系统的物理参数需要检测，而这通常是很困难的。

近年来，基于智能控制理论中的模糊逻辑、神经网络、遗传算法等知识形成了许多新型的建模方法，为电液伺服系统的建模开辟了一条新途径。T-S 模糊模型以局部线性化为基础，通过模糊推理方法实现了全局的非线性，具有结构简单、逼近能力强等特点，文献［8-9］利用T-S 模糊模型建立了电液伺服系统的模型，并基于该模糊模型提出了预测控制和H∞模糊跟踪控制方案。神经网络是一种具有高度非线性的连续时间动力系统，它有着很强的自学习功能和对非线性系统的强大映射能力，文献［10］提出了基于Adaline 神经网络的电液伺服系统加速度谐波在线辨识算法。文献［11］利用神经网络构造了电液伺服系统的模型，得出了神经网络模型的精确性高于线性模型的结论。文献［12］采用自适应学习率的改进BP 算法在线调整网络权值，从而得到精度高、泛化能力强的电液伺服系统神经网络模型。

本文以某远程火箭炮泵控缸电液位置伺服系统为对象，研究了该电液伺服系统机理建模、模糊建模、BP 神经网络建模和基于遗传算法的BP 神经网络建模4 种建模方法，并利用辨识数据对各种模型进行了训练和检验，通过分析比较总结出了各模型的特点，为泵控缸电液位置伺服系统的内模控制、模型参考控制等奠定了基础。

1 泵控缸电液位置伺服系统

某远程火箭炮泵控缸电液位置伺服系统结构图如图1所示。该系统主要由火控计算机、控制计算机、D/A 转换器、功率放大器、液压系统(包括伺服阀、伺服泵、液压缸和储能器等)、旋转变压器、RDC模块等组成。

图1 泵控缸电液位置伺服系统结构图Fig.1 The diagram of the electro-hydraulic position servo system of pump-controlled cylinder

数据是辨识的基础，因此，要首先确定系统的输入/输出数据。在系统辨识中，最常用也最容易形成的是伪随机二进制信号。由于伪随机二进制信号仅包括两个幅值，因此被广泛的应用于线性系统的辨识中。而对于非线性系统，Leontaritis 和Billings［13］已经证明:用伪随机二进制信号作为激励信号，系统的一些特性将会丢失。对于非线性系统辨识，激励信号应该是各种幅值和频率的组合，而伪随机多幅值信号恰好符合这一要求。伪随机多幅值信号可以由(1)式计算得到［14］

式中:int(x)表示将x 取整;v(y)是方差为σ2的白噪声序列;Ns是保持相同幅值的步数。

在实际应用中，大多数控制输入并不是在固定时间内保持某一幅值的，为此引入一个变量δ 来决定何时改变幅值，则w(k)为

由(2)式可知，δ 越趋近于1，则激励信号保持某一恒定值的时间越长，即该激励信号具有较低的频率特性，反之激励信号具有较高的频率特性。

2 泵控缸电液位置伺服系统建模方法

2.1 机理建模

在机理建模之前，先作如下假设:1)泵和缸的泄漏为层流，壳体回油压力为零，忽略低压腔向壳体内的外泄漏;2)忽略管道内压力损失和管道动态;3)补油系统的工作无滞后，在工作中低压管道压力不变，高压腔压力变化;4)在管道和缸体腔内不会出现压力饱和现象。

通过建立泵和缸流量连续方程、缸和负载力矩平衡方程便可推导出泵控缸电液位置伺服系统的传递函数。

2.1.1 泵和缸流量连续方程

控制电压为U 时，变量泵的摆角φ 为

式中，K 为电压—角度转换系数。

泵和缸的流量连续性方程为

式中:kp为变量泵排量梯度;np为变量泵转速;p1为负载压力;Ct为总泄漏系数;A 为负载液压缸活塞缸筒有效面积;l 为负载液压缸活塞缸筒位移量;V0为一个腔的容积;βe为有效体积弹性模数。

图1中B 点的运动轨迹是曲线，可以通过余弦定理建立液压缸活塞缸筒线速度dl/dt 与负载角速度dθ/dt 之间的转换关系

式中:θ 为负载的转角;Klθ(θ)是将线速度转换为角速度的比例系数。

因此，(4)式可以改写为

2.2.2 缸和负载力矩平衡方程

缸和负载力矩平衡方程

式中，De为等效排量;J 为转动惯量;Bm为粘性阻尼系数;G 为负载弹性刚度;TL为不平衡力矩。

2.2.3 泵控缸电液位置伺服系统传递函数

将(6)式和(7)式求拉氏变换后联立、略去负载弹性刚度G，并化简得

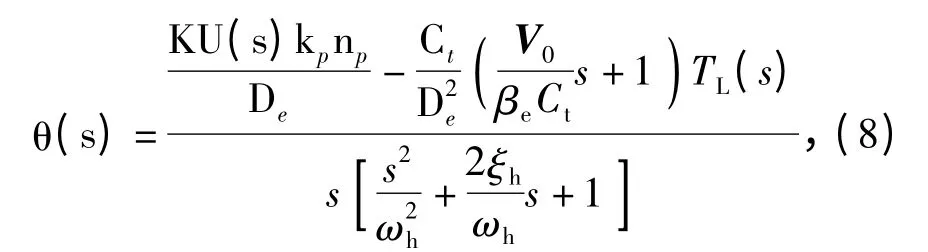
式中:ωh=为液压系统固有频率;为液压系统阻尼系数。

在(8)式中，系统转动惯量J 随着带弹量的不同而大范围变化，且总泄漏系数Ct、油液粘性阻尼系数Bm和不平衡力矩TL等均随工作状态而变化，这说明泵控缸电液位置伺服系统存在严重的非线性和时变性。

由(8)式可知，控制电压与负载转角之间的传递函数为

2.2 模糊建模

常用的模糊模型为Mamdani 模型和Takagi-Sugeno(T-S)模型。Mamdani 模型经常用在专家系统中，而T-S 模糊模型规则前件是模糊变量，结论部分是输入输出线性函数，它以局部线性化为基础，通过模糊推理方法实现了全局的非线性，因此，本文采用模糊c 聚类法划分输入空间、利用最小二乘法辨识结论参数，以构造T-S 模糊模型逼近泵控缸电液位置伺服系统。

1)T-S 模糊模型前提结构辨识

模糊c 均值(FCM)类型算法的价值函数为

式中:vij介于(0，1)之间;ci为模糊组i 的聚类中心;dij=‖ci-xj‖为第i 个聚类中心与第j 个数据点间的欧几里德距离;m∈(1，μ)是一个加权指数。

构造如下新的目标函数，可使得(10)式达到最小值的必要要求

式中，λj(j=1，…，n)是的第n 个约束式的拉格朗日乘子。对所有输入参量求导，使得(10)式达到最小的必要条件为

和

由上述两个必要条件，模糊c 聚类算法是一个简单的迭代过程。

FCM 用下列步骤确定聚类中心ci和隶属度矩阵V:

步骤1 用值(0，1)之间的随机数初始化隶属度矩阵V，使其满足约束条件;

步骤2 用(12)式计算c 个聚类中心ci，i=1，…，c;

步骤3 根据(10)式计算价值函数。如果它小于某个确定的阈值，或它相对上次价值函数值的改变量小于某个阈值，则停止算法;

步骤4 用(13)式计算新的V 矩阵，返回步骤2.

2)模糊模型结论参数辨识

模糊模型的结论参数利用最小二乘法求取。

2.3 BP 神经网络建模

由于BP 神经网络可以逼近任意非线性系统，所以采用三层网络BP 算法来建立非线性系统的模型。

BP 神经网络训练集的设计:

1)输入层节点数选择。从系统输入输出关系和辨识精度考虑，采用4 个输入结点，即u(k)，u(k-1)，y(k)和y(k-1).

2)隐含层及输出层节点数选择。隐含层结点数目的选择对辨识网络精度有很大的影响，本文按照公式得到隐含层结点数的初值为6.其中，nh为隐含层结点数，n 为输入层结点数，m 为输出层结点数，a 为［1，10］之间的自然数。输出层节点数为1.因此，用于辨识的网络结构为4-6-1.

3)初始权值。如果每个节点的净输入均在零点附近，则网络的学习速度较快。为了使各节点的初始净输入在零点附近，有两种办法可以采用:一种是初始权值足够小;另一种是使初始权值为1 和-1的权值数相等。本文中采用第一种方法设置初始权值。

4)神经网络训练。为了减小神经网络学习过程的振荡趋势，改善收敛性，本文采用带有动量项的BP 算法训练网络节点的权值和阈值，即

式中:ω(k)为权值;η 为学习率;D(k)=-∂J/∂ω(k)为k 时刻的负梯度，J 为性能指标函数;α 为动量因子，且0≤α ＜1.

2.4 基于遗传算法的BP 神经网络建模

BP 算法的优点是计算数值精度高，缺点是易陷入局部最优，并且对网络结构的初值要求高，初值不合理会引起网络振荡以至不收敛，而遗传算法具有全局随机搜索能力，能够在复杂的、多峰值的及不可微的大矢量空间中迅速有效地寻找到全局最优解，陷入局部最小值的可能性大大减少。因此，将遗传算法与神经网络相结合(GA-BP)，较好的解决了BP神经网络易陷入局部最小的问题。

遗传算法实现BP 神经网络权值和阈值优化的关键技术:

1)编码方式。根据实际情况在采用实数编码方式时，每个权值和阈值分别由1 个符号位、1 个整数位和4 个小数位组成:第1 位为符号位，其取值为随机产生的0 或1，定义0 表示正号，1 表示负号;第2 位为整数位，由多次训练结果可知，每个权值和阈值的取值范围在(-4，4)之间，因此，整数位的取值是随机产生的［0，3］之间的整数;第3 位到第6 位为小数位，其取值为随机产生的［0，9］之间的整数。

2)适应度函数。本文将性能指标函数J 引入适应度函数的计算，可以充分地把两者的评估标准融为一体。定义适应度函数F 为:

式中，Cmax为足够大的常数。

3)遗传操作。选择算子采用适用度比例法;交叉算子采用两点交叉算法;变异算子采用基本位突变的变异操作:首先对个体的每一个基因座以变异概率Pm指定其为变异点，然后对每一个指定的变异点，对其基因值做取补运算，从而产生新一代个体。由于本文中编码的符号位、整数位和小数位的取值范围不同，因此在执行变异操作时要按编码位的性质采用不同的变异策略:符号位模1 取补、整数位模3 取补、小数位模9 取补。

3 实验仿真

考虑到泵控缸电液位置伺服系统的固有频率较低，本文选择(2)式中变量δ=0.9，并且由于泵控缸电液位置伺服系统随动控制箱的控制输出电压为-5～5 V，因此，伪随机多幅值信号的幅值范围也应在-5～5 V 之间。将(2)式所产生的伪随机多幅值信号由功率放大器放大后，输入到泵控缸电液位置伺服系统的半实物仿真试验台，并由测角装置实时测量火箭炮负载的角度值，便可得到一组系统输入/输出数据对，如图2所示，图中(a)为伪随机多幅值输入数据，(b)为火箭炮负载角位置输出数据。

图2 泵控缸电液位置伺服系统输入输出数据Fig.2 The input/output data of the electro-hydraulic position servo system of pump-controlled cylinder

图2中的4 000 组输入/输出数据(采样间隔为0.1 s)作为训练数据和检验数据，其中前2 200 组数据用来训练，后1 800 组数据用来检验。

3.1 机理建模

经过辨识，泵控缸电液位置伺服系统的传递函数为

图3为机理建模模型输出和期望输出，其中(a)为训练数据，(b)为检验数据。训练的均方根误差RMS(用于衡量模型的精确性，RMS 值越小，表示模型越好，越接近于实际系统)为5.23，信号间方差比VAF(用于衡量模型输出近似于期望输出的程度，VAF 值越大，表示模型越好，越接近于实际系统)为78.56%;检验的RMS 为7.423，VAF 为51.27%.由RMS 和VAF 数据可知，机理建模得到的模型精度低、泛化能力差，只能粗略地描述泵控缸电液位置伺服系统固有的非线性和时变性特性。

图3 机理建模模型输出和期望输出Fig.3 The model output and desired output of mechanism modeling

3.2 模糊建模

利用模糊c 聚类方法划分输入空间、最小二乘法辨识结论参数，从而构造模糊模型。令模糊聚类个数的初值为c=3.模糊建模模型输出和期望输出如图4所示，其中(a)为训练数据，(b)为检验数据。训练的RMS 为0.42，VAF 为98.25%;检验的RMS为0.73，VAF 为97.68%.由RMS 和VAF 数据可知，模糊建模得到的模型精度较高、泛化能力较好，可较好的拟合泵控缸电液位置伺服系统固有的非线性和时变性特性。

图4 模糊建模模型输出和期望输出Fig.4 The model output and desired output of fuzzy modeling

令BP 神经网络的学习速率η=0.05，最大训练次数为1 000.考虑到神经网络初值不同对建模结果的影响，因此，本文利用BP 神经网络进行了10次建模研究，并对10 次建模结果取平均值。BP 神

3.3 BP 神经网络建模

经网络建模模型输出和期望输出如图5所示，其中(a)为训练数据，(b)为检验数据。训练的RMS 为0.30，VAF 为98.72%;检验的RMS 为0.51，VAF 为98.44%.由RMS 和VAF 数据可知，神经网络建模可较好的拟合泵控缸电液位置伺服系统固有的非线性和时变性特性，得到的模型建模精度较高、泛化能力较好。

图5 神经网络建模模型输出和期望输出Fig.5 The model output and desired output of BP neural network modeling

3.4 基于遗传算法的BP 神经网络建模

令BP 神经网络的学习速率η=0.05，群体规模为25，交叉概率Pc=0.8，变异概率Pm=0.1，最大训练次数为1 000.基于遗传算法的BP 神经网络建模模型输出和期望输出如图6所示，其中(a)为训练数据，(b)为检验数据。训练的RMS 为0.07，VAF 为99.58%;检 验 的RMS 为0.13，VAF 为99.47%.由RMS 和VAF 数据可知，基于遗传算法的BP 神经网络建模得到的模型精度高、泛化能力好，能够很好的描述泵控缸电液位置伺服系统的动态特性。

图6 基于遗传算法的BP 神经网络建模模型输出和期望输出Fig.6 The model output and desired output of BP neural network modeling based on genetic algorithm

4 结论

本文研究了某远程火箭炮泵控缸电液位置伺服系统的机理建模、智能建模的方法，并建立了其机理建模模型、模糊模型、BP 神经网络模型和基于遗传算法的BP 神经网络模型。通过对比RMS 和VAF数据可知，由机理建模方法推导出的线性传递函数几乎不能描述系统的非线性和时变性特性，建模精度低、泛化能力差。模糊建模和BP 神经网络建模建模精度较高、泛化能力较好，可较好的拟合系统固有的非线性和时变性特性，但是模糊建模时聚类算法对于设置聚类中心的初值存在一定困难;神经网络建模存在易陷入局部最优，并对网络初值要求高等问题。基于遗传算法的BP 神经网络较好的解决了BP 神经网络易陷入局部最小的问题，因此，基于遗传算法的BP 神经网络建模能够很好的描述系统的动态特性，具有建模精度高、泛化能力好的特点。

References)

［1］ Vossoughi G.Nonlinear analysis and control of electro-hydraulic servo system［C］∥Proceedings of the 2nd Biennial European Joint Conference on Engineering Systems Design and Analysis，New York，1994:59-67.

［2］ Bennett S.Brief history of servome chanisms［J］.IEEE Control System Magazine，1994，14:75-79.

［3］ Sepasi M，Sassani F.On-line fault diagnosis of hydraulic systems using unscented kalman filter［J］.International Journal of Control，Automation and Systems，2010，8(1):149-156.

［4］ Kalyoncu M，Haydim M.Mathematical modelling and fuzzy logic based position control of an electrohydraulic servosystem with internal leakage［J］.Mechatronics，2009，19(6):847-858.

［5］ 管成，潘双夏.电液伺服系统的非线性鲁棒自适应控制［J］.中国电机工程学报，2007，27(24):107-112.GUAN Cheng，PAN Shuang-xia.Nonlinear robust adaptive control of electro-hydraulic system［J］.Proceedings of the Chinese Society for Electrical Engineering，2007，27(24):107-112.(in Chinese)

［6］ 方一鸣，韩永成，赵琳琳，等.控制量前具有不确定系数的电液伺服系统自适应控制［J］.控制理论与应用，2009，26(2):156-160.FANG Yi-ming，HAN Yong-cheng，ZHAO Lin-lin，et al.Adaptive controller for electro-hydraulic servo system with uncertain coefficients in control input［J］.Control Theory ＆ Applications，2009，26(2):156-160.(in Chinese)

［7］ 倪敬，彭丽辉，项占琴.扩轧管电液伺服系统非线性建模与控制［J］.机械工程学报，2009，45(5):250-255.NI Jing，PENG Li-hui，XIANG Zhan-qin.Nonlinear modeling and control of electro-hydraulic servo system of pipe expanding［J］.Journal of Mechanical Engineering，2009，45(5):250-255.(in Chinese)

［8］ Shen Y L，Cao Y，Li T S.Study on electrohydraulic servo loading system using fuzzy model based predictive control with multi-step linearization［C］∥Proceedings of the World Congress on Intelligent Control and Automation，Shanghai:2002:312-315.

［9］ Zhang X Z.H∞tracking control to electrohydraulic servo system of continuous casting mould based on fuzzy models［C］∥Fifth World Congress on Intelligent Control and Automation，Hangzhou:2004:769-772.

［10］ 姚建均，王立权，王贤成，等.基于人工神经网络的电液伺服系统加速度谐波辨识［J］.兵工学报，2009，30(5):633-638.YAO Jian-jun，WANG Li-quan，WANG Xian-cheng，et al.Electrohydraulic servo system acceleration harmonic estimation based on ANN［J］.Acta Armamentarii，2009，30(5):633-638.(in Chinese)

［11］ He S，Sepehri N.Modeling and prediction of hydraulic servo actuators with neural networks［C］∥Proceedings of American Control Conference，San Diego:1999:3708-3712.

［12］ 张秀玲.液压弯辊系统的优化神经网络内模控制［J］.中国机械工程，2007，18(20):2419-2421.ZHANG Xiu-ling.Optimal neural network internal model control for hydraulic bending roll system［J］.China Mechanical Engineering，2007，18(20):2419-2421.(in Chinese)

［13］ Leontaritis I J，Billings S A.Experimental design and identifiability for nonlinear system［J］.International Journal of Systems Science，1987，18:189-202.

［14］ Mohieddine J，Andreas K.Hydraulic servo-system modeling，identification and control［M］.London:Springer-Verlag London Limited，Library of Congress Cataloging-in-Publication Data，2003:132-134.