水下滑翔机纵倾运动的自适应积分反演控制

陈宇航，严卫生，高剑，杜亮

(西北工业大学 航海学院，陕西 西安710072)

0 引言

浮力驱动式水下滑翔机依靠移动内部质量块和改变压载舱质量(浮力调节)实现水下锯齿形滑翔运动［1］如图1所示。俯仰角的跟踪控制对于水下滑翔机完成水下侦察、海洋观测、海底地形绘制等任务具有重要的意义。Naomi 等人［2］基于试验级水下滑翔机“ROGUE”的线性化模型提出了LQR 最优控制方法。Graver［3］系统分析了滑翔机的结构及水下运动特性，针对“ROGUE”滑翔机进行了更深入的研究，提出了滑块加速度的控制模式。Nina 等人［4］运用PID 控制方法设计了前馈/反馈控制器对滑翔机的运动进行了分析。以上的研究对于滑翔机非线性模型均采用了线性化的方法，没有考虑模型中的非线性特性和参数的不确定性。

近十几年来，反演设计方法作为非线性反馈控制系统的一种递归设计方法，已经成为不确定非线性系统控制的有效方法。反演技术是一种基于Lyapunov 稳定性理论的非线性控制递推设计方法，但寻找一个合适的Lyapunov 函数却一直缺少系统化的方法，而反演设计方法则提供了一种有效的途径，其基本思想是将复杂的非线性系统分解为不超过系统阶数的子系统，然后从系统输出开始为每个子系统设计Lyapunov 函数和虚拟控制量，一直“反演”到系统的控制输入，实现系统的全局渐近跟踪。

本文针对水下滑翔机纵倾运动非线性模型参数不确定情况下，研究了滑翔机俯仰角跟踪控制问题，控制律的设计分为两步:第一步，采用了自适应积分反演控制方法，对于不确定模型参数进行在线估计，设计滑块位移控制律;第二步，由于反演控制具有良好的过渡过程品质，将得到的滑块位移作为滑块伺服控制器的参考输入，利用反演控制方法设计滑块伺服控制器，跟踪滑块位移参考输入。仿真研究显示，该方法获得了良好的系统动态性能，保证了俯仰角跟踪误差的全局渐近稳定。

1 水下滑翔机纵倾运动模型

水下滑翔机的动力学模型［6］有着很强的非线性性，较为复杂，不便于控制系统的设计，为简化问题的分析，作下面几点假设［7］:

1)质量块相对于滑翔机质量比较小，滑块的纵向偏移量较小，且轴向位移及轴向移动速度较小，则由于滑块移动引起的惯性主轴的变化ΔJ 可忽略不计，即滑翔机的转动惯量=J2+ΔJ≈J2为常数，并忽略滑块轴向移动牵连力和科氏力的影响。

2)考虑到滑翔机速度的慢变特性，忽略速度的动态性能。

3)俯仰角θ∈(-π/2，π/2)

根据以上的假设，水下滑翔机的纵倾运动模型可以描述为

式中，ω2为俯仰角速度;J2为转动惯量;mf1、mf3为附加质量;ms，s、r 分别为滑块的质量和在载体坐标系下的位置(r 为固定值);α 为攻角;v1、v3为滑翔机在载体坐标系下的轴向和纵向速度;KM为水动力系数;u 为滑块的轴向控制力。

为便于分析，将模型(1)改写为

模型(2)中包含不确定参数β，γ，δ.

2 自适应反演控制器设计

水下滑翔机纵倾运动控制律设计的基本思想是:首先根据给定俯仰角参考信号θr，利用自适应反演控制方法设计滑块期望轴向位置sr，使得θ 能够快速的全局渐近收敛到θr，进而以sr为参考输入，设计控制律u，使得s 能够快速的跟踪sr.

2.1 俯仰角跟踪控制器设计

第一步，定义俯仰角度跟踪误差

求导有

以角速度ω2为虚拟的控制输入，使e1具有适当的稳定特性，选择稳定函数

式中:c1，λ1为正的设计参数;ζ1为积分项，定义为增加的积分项可以增强系统在干扰和模型参数不确定情况下的动态性能的鲁棒性。

第二步，定义角速度的跟踪误差

由(4)式和(6)式得

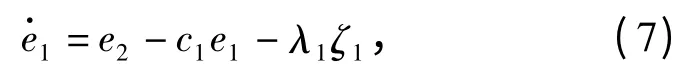
选择Lyapunov 函数

求导有

对(6)式求导有

将(2)式、(5)式代入(10)式有

选择第二个Lyapunov 函数

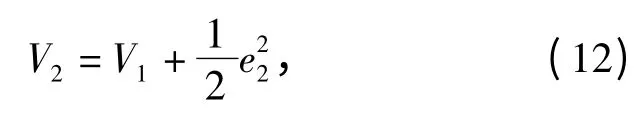
求导有

将(9)式、(11)式代入(13)式有

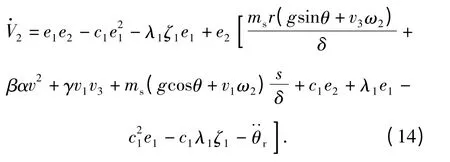
为获得期望的稳定特性，考虑到不确定参数β，γ，δ，选择滑块位移参考输入sr为

式中，当θ 为±90°时，ms(gcos θ+v1ω2)=0，在假设条件下为未知参数的估计值，为对应的估计误差，c2，λ2为正的设计参数，ζ2为积分项，定义为

将(15)式代入(14)式得

式中，

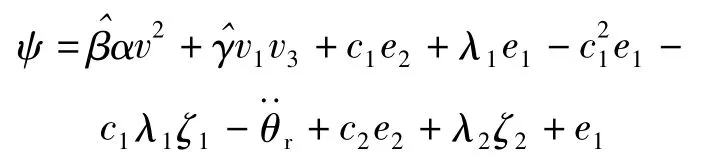
为消除参数估计对于系统稳定性的影响，设计参数自适应律，选择第三个Lyapunov 函数

式中，ε1，ε2，ε3为自适应参数，对上式求导有

将(16)式代入(18)式有

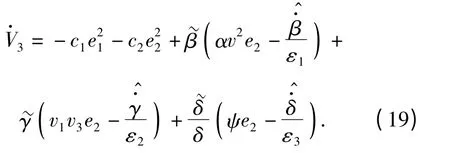
选择如下的自适应律

将(20)式代入(19)式得

由于标量函数V3正定，而负半定且对时间是一致连续的，根据Barbalat 引理有

由以上分析可知，(2)式描述的水下滑翔机纵倾运动在控制律(15)式及自适应律(20)式的作用下，能够跟踪指定的俯仰角参考信号，并且俯仰角跟踪误差全局渐近收敛到零。

2.2 滑块伺服控制器设计

滑块的轴向位移为s，滑块在u 的作用下全局渐进跟踪期望位移sr，由滑块位移的作用可知，sr更应该视为一种静态量，忽略其动态特性，结合(15)式运用反演法进行滑块伺服控制器设计。

第一步，定义滑块位移跟踪误差

求导有

定义滑块轴向移动速度的跟踪误差

由(24)式和(25)式可知

选择Lyapunov 函数

求导有

对(26)式求导有

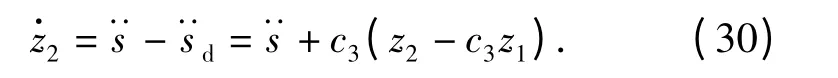
选择第二个Lyapunov 函数

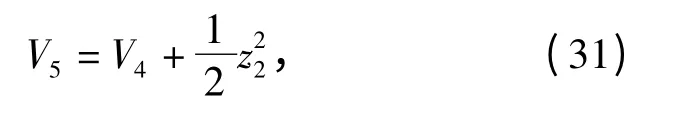
求导有

取控制输入

则有

根据Barbalat 引理有

由以上分析可知，(2)式描述的滑块轴向运动在控制律(33)式作用下，能够跟踪滑块位移参考信号，并且位移跟踪误差全局渐近收敛到零。

反演控制具有良好的过渡过程品质，滑块在控制律(33)式的作用下，跟踪参考输入sr，并保证s=sr，而在控制律(15)式及自适应律(20)式的作用下，最终保证俯仰角跟踪的全局渐近稳定性。

3 仿真研究

通过仿真实验验证上述的自适应积分反演跟踪控制器及滑块伺服控制器的性能，并分析引入的积分项对于控制系统的性能的影响，控制器设计框图如图2所示。

图2 水下滑翔机纵倾运动控制示意图Fig.2 Underwater glider vertical pitch motion control schematic

仿真中，取水下滑翔机运动模型参数KM=-100 Nm(s/m)2，J2=12 kg·m2，mf1=5 kg，mf3=70 kg，ms=9 kg，r=0.05 m，俯仰角参考指令取为

1)选取控制参数λ1=1，λ2=1，c1=2，c2=2，c3=15，c4=15，参数自适应估计的初值为，=-8，=5.4=-12，自适应参数ε1=ε2=ε3=0.1.

从仿真结果可以看出，俯仰角和滑块位移能够快速的跟踪给定的参考值如图3所示。同时，俯仰角及滑块位移跟踪误差渐近收敛到零如图4所示。

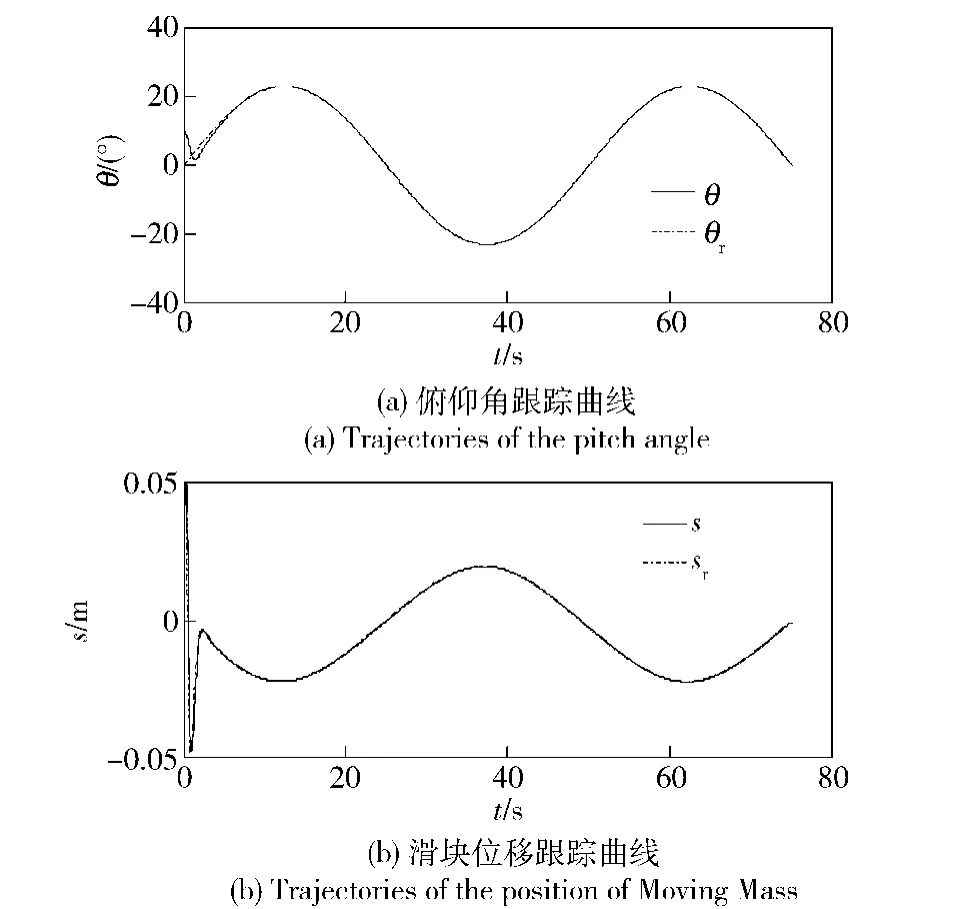
图3 俯仰角、滑块位移跟踪曲线Fig.3 Trajectories of the pitch angle and position of Moving Mass

2)对比有积分项，即λ1=1，λ2=1 和无积分项，即λ1=0，λ2=0 时的控制系统的响应性能，其他控制参数与上述相同。

图4 俯仰角及滑块位置跟踪误差Fig.4 Pitch tracking error and position tracking error of Moving Mass

仿真结果如图5所示，积分项的引入提高了俯仰角跟踪精度，但增大了系统的超调。

图5 积分项对于系统性能的影响Fig.5 Integral on the performance of the system

上述仿真结果显示，在俯仰角控制律和自适应律及滑块伺服控制器的作用下，俯仰角和滑块位移能够快速的跟踪给定的参考值。同时，俯仰角及滑块位移跟踪误差收敛到零。自适应积分反演控制保证了在模型参数不确定的情况下跟踪误差的全局渐近稳定性，积分项的引入，则进一步提高了系统在不确定参数及未建模动态下的鲁棒性。

4 结论

本文研究了水下滑翔机纵倾运动的俯仰角跟踪控制问题，采用自适应积分反演控制方法，设计了俯仰角跟踪控制器及滑块伺服控制器。理论分析和数学仿真都证明了在所设计的控制律和自适应律的作用下，闭环控制系统具有全局渐近稳定性，而积分项的引入则可以进一步改善稳态控制品质。水下滑翔机所处海洋环境复杂，如海流的影响等，在存在随机干扰和模型参数不确定的情况下，自适应和滑模控制的结合将是一个值得探索的解决方案。另外，滑翔机的编队控制，路径跟踪，路径规划等在未来的工作中也将做进一步的研究探讨。

References)

［1］ Jenkins S A，Humphreys D E，Sherman J，et al.Underwater glider system study［R］∥Scripps Institution of Oceano-graphy Technical Report.UC San Diego:Scripps Institution of Oceanography，2003.

［2］ Naomi E L，Joshua G G.Model-based feedback control of autonomous underwater gliders［J］.IEEE Journal of Oceanic Engineering，2001，26(4):643-645.

［3］ Joshua G G.Underwater gliders:dynamics，control and design［D］.Princeton:Princeton University，2005.

［4］ Nina M，Craig W.Under water glider motion control［C］.Proceedings of the 47th IEEE Conferenceon Decision and Control，2008:552-557.

［5］ Smallwood D A，Whitcomb L L.Model based dynamic positioning of underwater robotic vehicles:theory and experiment［J］.IEEE Journal of Oceanic Engineering，2004，29(1):1-19.

［6］ Woolsey C A，Leonard N E.Moving mass control for underwater vehicles［C］∥Proceedings of the American Control Conference，May 8-10，2002.

［7］ Liao G B，Yu B S，Yang Y G.Study on the theory and simplified equations of mass moment control missile［J］.System Engineering and Electronics，Nov，2004，26(11):1635-1639.

［8］ Jean-Jacques E.Slotine，Weiping Li.Applied nonlinear control［M］.Beijing:China Machine Press，2006.

［9］ 严卫生.鱼雷航行力学［M］.西安:西北工业大学出版社，2005.YAN Wei-sheng.Torpedo navigation mechanics［M］.Xi’an:Northwestern Polytechnical University Press，2005.(in Chinese)