车辆动力传动系统扭转强迫振动响应灵敏度研究

刘辉，蔡仲昌，曹华夏，项昌乐

(北京理工大学 机械与车辆学院 车辆传动国家重点实验室，北京100081)

0 引言

在车辆动力传动系统设计中，为使系统具有较好的动态特性，需对设计参数进行反复的动力学修改和优化，而灵敏度分析将使这些工作更具有针对性、可行性［1-5］。目前系统动力特性灵敏度研究主要是针对固有频率和振型展开，主要有以下两种方法，一是借助模态分析中特征值和特征向量灵敏度分析方法［6-8］，二是在大型商用有限元软件中采用优化设计模块提供的梯度评估工具［9-10］。而动态响应灵敏度分析主要借助于模态分析中频响函数灵敏度分析或在模态分析基础上结合傅里叶变换进行，涉及大量复杂矩阵运算，推导过程繁琐，计算困难［11-12］。因此一种原理简单、推导方便、计算快捷的适合于动力传动系统轴系的扭振响应灵敏度分析方法更具有工程实际意义。车辆动力传动系统扭转强迫振动响应灵敏度分析主要是研究强迫振动响应参数如扭振角位移和附加扭振应力对惯量、刚度等系统结构参数的变化率。本文在利用系统矩阵法对车辆动力传动系统多自由度集中参数模型进行扭振响应分析的基础上，运用直接导数法进行强迫振动响应灵敏度分析，推导了强迫振动响应灵敏度计算公式，建立了一套适合于动力传动系统的强迫振动响应灵敏度分析方法，通过实例验证了该方法的可行性。

1 动力传动系统强迫振动响应分析

本文采用集中参数法对车辆动力传动系统进行多自由度离散化分析，以发动机波动转矩为激励，建立系统n 自由度强迫振动模型，其动力学方程为

式中，J、K 和C 分别为n ×n 阶的系统惯量矩阵、阻尼矩阵和刚度矩阵;θ、和分别为n 维的系统扭振角位移、角速度和角加速度列向量;M 为系统激励转矩向量。

作用在发动机曲轴上的波动转矩是车辆传动系统产生扭振的能量来源，其主要包括燃气爆发压力转矩和往复部件惯性转矩，一般通过傅里叶级数展开得到波动转矩的各谐次信息。发动机第v 谐次(v=r/2(r=1，2，…，24))转矩及系统在其作用下的扭振角位移响应和综合角位移响应分别为

式中，v 为发动机转矩各谐次序号，Xv和Yv分别为发动机第v 谐次波动转矩的余弦、正弦分量矩阵，ω 为发动机旋转角速度，t 为时间。

角位移分别对时间取一阶、二阶导数得到动力传动系统扭振角速度和角加速度响应。

根据各质量点振幅和材料力学公式，可得忽略轴段材料阻尼时，第l 轴段(l=1，2，…，n-1)的附加扭振应力为

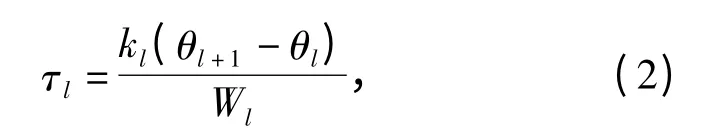
式中:θl为第l 轴段的综合角位移响应;Wl为第l 轴段的抗扭截面模量;kl为第l 轴段的扭转刚度。

2 强迫振动响应灵敏度分析

2.1 灵敏度分析方法

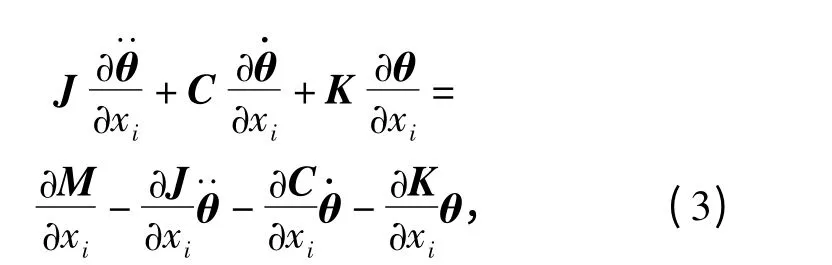
引入广义力

则(3)式可表示为

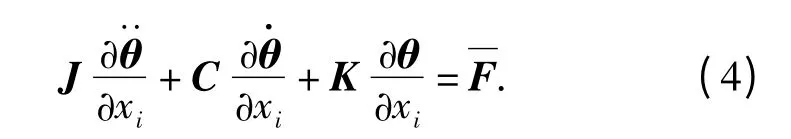
2.2 扭转角位移对设计参数的灵敏度

取扭转刚度kl为设计变量，则(3)式化为

2.3 轴段附加扭振应力对设计参数的灵敏度

取扭转刚度kh为设计变量，将(2)式对kh求导得

当h≠l 时，

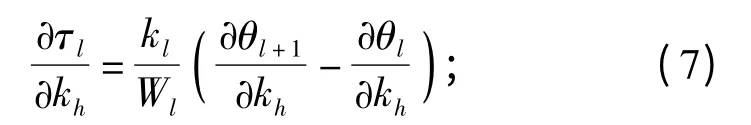
当h=l 时，

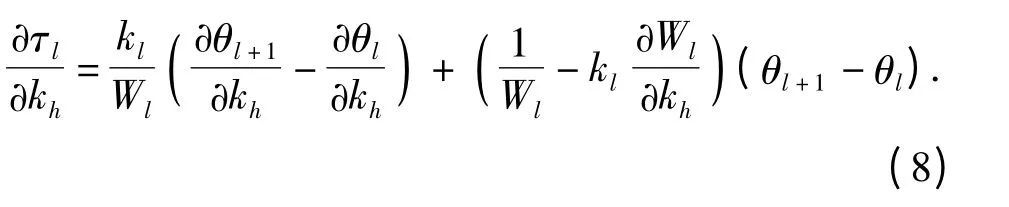
为便于比较各个参数对振动特性的影响，引入相对灵敏度概念，采用一阶无量纲灵敏度进行分析，表达式为

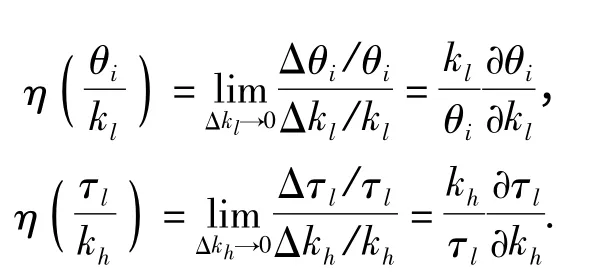
本文根据前面推导的灵敏度公式，采用Matlab编程对强迫振动响应对刚度的灵敏度进行计算，计算程序流程如图1所示。

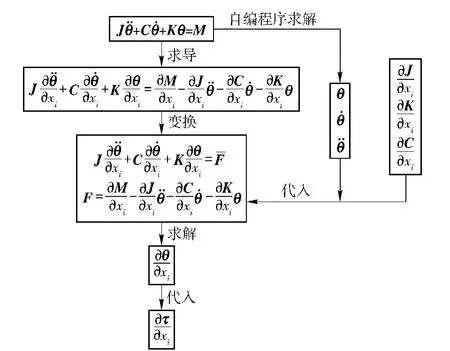
图1 灵敏度分析计算流程Fig.1 Flow chart of sensitivity analysis for vibration response

3 强迫振动响应灵敏度分析实例

3.1 强迫振动响应分析

某车辆动力传动系统简化为81 个自由度的模型，其某挡的扭振计算模型如图2所示。图中n 为集中质量点个数，即系统自由度个数，Ji为各集中质量点的惯量(i=1，2，…，m，…，p，…，n)，kl为各轴段扭转刚度，阻尼的位置和表示方法与刚度相同，在此不再赘述。

扭振振幅计算结果如图3所示。由图可知，发动机自由端和飞轮的振幅随着转速增加呈下降趋势，在发动机转速600 r/min 时达到最大值0.6°和0.55°，振动以0.5 谐次为主;变速箱输入端振幅最大值为0.52°，在发动机转速范围0.5、1、1.5、3、4.5谐次均存在共振转速。

图2 车辆动力传动系统某档扭振计算模型Fig.2 Torsional vibration dynamic model of powertrain

图3 不同部件的扭振角位移振幅Fig.3 Vibration amplitudes in different components

通过计算可知，曲轴系统中第6 轴段附加扭振应力最大，传动系统中第11 轴段附加扭振应力最大。它们在发动机工作转速范围内的最大附加扭振应力如图4所示。

图4 不同轴段的附加扭振应力Fig.4 Maximal additional vibration stress in different shafts

3.2 强迫振动响应灵敏度分析

在工程实际中，由于受到实际结构的限制，优先采用调整轴段刚度的方法进行动力学修改。发动机自由端、飞轮和变速箱输入端振幅对轴段刚度的灵敏度结果如图5所示。从结果可知，发动机自由端振幅依次对减振器、联轴器、曲轴系统轴段的刚度敏感;发动机飞轮振幅依次对第13 轴段、联轴器、传动系统轴段、曲轴系统轴段的刚度敏感;变速箱输入端振幅依次对联轴器、第13 轴段、传动系统轴段的刚度敏感。

轴段附加扭振应力τ6、τ11对各轴段刚度的灵敏度计算结果如图6所示。由图可知，τ6依次对减振器、联轴器、曲轴系统轴段的刚度敏感;τ11依次对联轴器、第13 轴段、传动系统轴段的刚度敏感。

以上分析表明当动力传动系统装有合适刚度的盖斯林格联轴器时，曲轴上各质量点的扭振角位移主要对曲轴系统本身的刚度敏感，而传动系统各质量点的扭振角位移主要对联轴器刚度和传动系统本身的刚度敏感，这表明位于联轴器前后的曲轴系统和传动系统在扭振性能上没有发生强烈耦合，相互影响很小，联轴器起到了很好的隔振作用。

从上述灵敏度分析可知，对于本文中实例，可以通过调整联轴器和第13 轴段的扭转刚度减小扭振角位移幅值和附加扭振应力。从工程实现角度分析，联轴器位于发动机飞轮和变速箱输入端之间，在动力学修改时比较容易实现;而第13 轴段为传动系统内部轴段，受到结构设计限制，难以实现较大幅度修改。在本例中，为改善系统振动响应特性，应当选择联轴器刚度作为动力学修改或优化的设计变量。

图5 不同部件振幅对轴段刚度的灵敏度Fig.5 Sensitivity of Vibration amplitude of different components to torsional stiffness

图6 附加扭振应力对轴段刚度的灵敏度Fig.6 Sensitivity of maximal additional vibration stress of different shafts to torsional stiffness of shafts

4 结论

本文基于车辆动力传动系统扭转强迫振动计算方法，对扭振角位移和附加扭振应力的灵敏度分析方法进行了深入研究，结论如下:

1)基于直接求导法，推导了扭振角位移和附加扭振应力对轴系刚度的灵敏度计算公式，提出了扭转强迫振动特性参数的灵敏度分析方法和流程，为动力传动系统扭振特性的动力学修改和优化中设计变量的选取提供了理论依据。

2)在动力传动系统中，位于弹性联轴器前后的曲轴系统和传动系统在扭振性能上没有发生强烈耦合，相互影响很小，弹性联轴器起到了较好的隔振作用。

3)以某型动力传动系统为实例进行了扭振特性和灵敏度分析，得到了扭振振幅和附加扭振应力的敏感参数，为该系统改善振动响应特性提供了指导。

References)

［1］ 毕凤荣，李志军，郝志勇.参数灵敏度分析在内燃机设计中的应用研究［J］.内燃机学报，2006，24(1):67-71.BI Feng-rong，LI Zhi-jun，HAO Zhi-yong.Application of parameter sensitivity analysis in internal combustion engine design［J］.Transactions of CSICE，2006，24(1):67-71.(in Chinese)

［2］ 唐传茵，郭立新，李华，等.灵敏度在车辆动力学分析中的应用［J］.计算机仿真，2008，25(11):278-281.TANG Chuan-yin，GUO Li-xin，LI Hua，et al.Application of sensitivity method in vehicle dynamics［J］.Computer Simulation，2008，25(11):278-281.(in Chinese)

［3］ 向建华，廖日东，张卫正.基于灵敏度分析的内燃机曲轴扭振系统结构动力学修改［J］.内燃机工程，2007，28(6):66-69.XIANG Jian-hua，LIAO Ri-dong，ZHANG Wei-zheng.Structural dynamic modification of crankshaft torsional vibration system of IC engine base on sensitivity analysis［J］.Chinese Internal Combustion Engine Engineering，2007，28(6):66-69.(in Chinese)

［4］ 梁兴雨，舒歌群，李小倩，等.基于结构刚度灵敏度分析的油底壳结构改进［J］.内燃机工程，2009，30(1):84-87.LIANG Xing-yu，SHU Ge-qun，LI Xiao-qian，et al.Structure improvement of oil sump based on structural sensitivity analysis［J］.Chinese Internal Combustion Engine Engineering，2009，30(1):84-87.(in Chinese)

［5］ 柴国英，黄树和，岳文忠，等.基于灵敏度分析的曲轴扭振减振器优化设计［J］.农业工程学报，2009，25(5):105-108.Chai Guo-ying，Huang Shu-he，Yue Wen-zhong，et al.Optimal design for torsional vibration damper based on sensitivity analysis［J］.Transactions of the Chinese Society of Agricultural Engineering，2009，25(5):105-108.(in Chinese)

［6］ 马洪文，马彪.综合传动装置变速机构振动频率与敏感度分析［J］.机械强度，2002，24(4):489-492.MA Hong-wen，MA Biao.Vibration frequency and sensitivity analysis on shift mechanism of powershift steering transmission［J］.Journal of Mechanical Strength，2002，24(4):489-492.(in Chinese)

［7］ 劳耀新，侯之超，吕振华.发动机前端附件带传动系统频率灵敏度分析［J］.汽车工程，2006，28(5):477-481.LAO Yao-xin，HOU Zhi-chao，LÜ Zhen-hua.Frequency sensitivity analysis on belt drive system for front end accessories of engine［J］.Automotive Engineering，2006，28 (5):477-481.(in Chinese)

［8］ 刘辉，项昌乐，郑慕侨.车辆动力传动系固有特性灵敏度分析及动力学修改［J］.汽车工程，2003，(25)6:591-594.LIU Hui，XIANG Chang-le，ZHENG Mu-qiao.Sensitivity analysis and dynamic modification of natural characteristic in vehicle powertrain［J］.Automotive Engineering，2003，(25)6:591-594.(in Chinese)

［9］ 雷明准，陈剑，陈心昭，等.灵敏度分析方法在车身轻量化中的应用［J］.汽车工程，2009，31(7):682-685.LEI Ming-zhun，CHEN Jian，CHEN Xin-zhao，et al.The application of sensitivity analysis to vehicle body lightweighting［J］.Automotive Engineering，2009，31(7):682-685.(in Chinese)

［10］ 王庆，张以都，张洪伟，等.基于有限元的齿轮传动系统动力修改研究［J］.武汉理工大学学报，2008，30(9):120-123.WANG Qing，ZHANG Yi-du，ZHANG Hong-we，et al.Finite-element based dynamic modification for gear transmission［J］.Journal of Wuhan University of Technology，2008，30(9):120-123.(in Chinese)

［11］ 郭兴昕，赵进全，白辽江，等.非均匀耦合传输线瞬态响应灵敏度的分析方法［J］.西安交通大学学报，2009，43(8):72-75.GUO Xing-xin，ZHAO Jin-quan，BAI Liao-jiang，et al.Sensitivity analysis of the transient response of nonuniform coupled transmission lines［J］.Journal of Xi'an Jiaotong University，2009，43(8):72-75.(in Chinese)

［12］ 张军挪，王瑞林，李永建，等.基于灵敏度分析的机枪结构动力修改研究［J］.中北大学学报:自然科学版，2007，28(2):112-116.ZHANG Jun-nuo，WANG Rui-lin，LI Yong-jian，et al.Structural dynamical modification research of machine gun based on sensitivity analysis［J］.Journal of North University of China:Natural Science Edition，2007，28(2):112-116.(in Chinese)