基于并联式平台的船舶轴段定位及工作空间分析

兰君辉，李天匀，朱翔，李维嘉

1 华中科技大学船舶与海洋工程学院，湖北武汉430074

2 高新船舶与深海开发装备协同创新中心，上海200240

3 船舶与海洋工程水动力湖北省重点实验室，湖北武汉430074

0 引 言

在船舶建造阶段，推进轴系的安装直接影响船舶建造的周期［1-2］。目前，国内对于轴系安装工艺的研究工作已经较为详尽，刘宏伟［3］详细介绍了某集装箱船的轴系安装流程和校中方法，系统阐述了传统轴系安装工艺；张潮宏［4］等从不同角度研究了超长轴系校中安装工艺的若干关键技术，分析了各中间轴段的校中及中间轴承的定位要素。对于并联机构的正反解算法和空间运动方面的研究也有很多，张尚盈等［5］给出了正反解算法和Matlab/Simulink 实现的方法，并用具体的例子和数据来验证该算法的高效性；黄真等［6］系统地研究了并联机器人机构的空间结构，形成了较为完整的理论体系。刘兆磊等［7］基于目标位置估计的Cramer-Rao 界和几何精度稀释（GDOP），来研究组网的多异质非线性传感器系统中传感器和目标的相对位置对目标跟踪精度的影响；韩明等［8］对振动传感器定位的原理和方法进行了阐述，提出了多节点协同定位中最佳站址布局的方式；夏凌楠等［9］以扩展卡尔曼滤波（EKF）为框架，结合惯性传感器和视觉里程计提出一种定位算法，能够克服视觉定位和惯性定位的缺点，提高定位精度。刘征等［10］基于运动学正解分析矿用正铲液压挖掘机的水平挖掘时理论可达的工作空间；贺淑娟［11］采用蒙特卡洛法求出机械臂的可行位形空间，即自由区域，建立了路径安全性优化数学模型。

船舶推进轴系安装是在船舶下水后，以已安装到位的艉轴作为基准，确保偏移量和偏斜量在允许范围的前提下，以主机为基准对各轴段进行逐个校中并将相邻轴段通过法兰连接，要求轴段精确调整至与基准轴对中的目标位置。但采用人工吊装的传统方式自动化水平不高，要耗费大量的人力和工时，对于重量较大的尤其是超大型船舶推进轴系的精准安装及后期调整作业，该问题就更加突出。

为了将传统的人工吊装的模式转变为智能设备自动装配的模式，提高船舶轴系安装的自动化水平，设计了一种特殊的六自由度并联式平台（以下简称“平台”），用于辅助船舶推进轴系智能安装。本文拟在平台基础上建立轴段的传感器观测模型，提出利用三边质心定位算法对轴段进行定位研究，计算平台与轴段接触点的位置条件，通过分析平台各种工况极限位置条件得到轴段工作空间。

1 平台简介

在轴系校中时，主要是通过平移和旋转组合进行调整，使轴段实现位置和姿态的调整，从而到达目标安装位姿。而传统人工吊装的安装方式位姿调整不便、精确度不高、效率低、安装质量依赖于操作人员的工程经验，因此有必要设计一种精度高、位姿调整易实现、负载大、自动化程度高的模块化平台［8］。所设计的平台由2 个独立的运动机构、2 个旋转脚架、2 个托块、1 个控制柜、1 个遥控手柄和1 台计算机组成，总体结构如图1 所示。平台主要的传动机构为2 个独立的运动机构，单个运动机构可以独立地实现3 个自由度的平移运动。具体的性能参数如表1 所示。

运动机构直线导轨行程为150 mm，电动缸行程为80 mm。测量出位于2 个运动机构上的某2个固定侧面的距离和位于2 个运动机构上的某2个固定上表面之间的高度差这2 个初始参数，将2个独立的运动机构按照这2 个参数进行现场组装，即完成了平台的初始化。

表1 平台性能参数Table 1 Performance parameters of the platform

图1 平台总体结构Fig.1 The overall structure of platform

利用所设计的平台进行轴系安装时，通过计算机控制程序实现对轴段位姿的调整。控制包含2 个模式：使用控制手柄实时控制轴段的平移和旋转，此为遥控模式；在控制界面输入目标位姿的坐标和角度、运行程序，运动机构会在控制系统的驱动下自动到达目标位置和姿态，此为姿态模式。

基于所设计的平台搭建了轴系安装试验台架，如图2 所示。在进行轴系安装时，中间轴承固定在轴段上并与轴承座分离，当轴段在运动机构的驱动下到达目标位置和姿态时，通过精密调整垫铁来调整中间轴承与轴承座的位置，并用螺栓将轴承固定在轴承座上，旋转轴段使法兰装配孔对齐并用螺栓将其与基准轴连接，从而实现该轴段的安装。

图2 运动机构在试验台架上的布置Fig.2 Setup of the moving mechanism on the test bench

2 传感器观测模型

利用平台实现轴系的智能安装，首先需要借助传感器对轴段进行定位，在位姿调整过程中还要实时确定轴段与目标位姿之间的相对位置。本节以轴段调整的目标位置相对于传感器局部坐标系的位置和方向为观测量，拟建立基于传感器局部坐标系的观测理论模型，作为轴段位置识别与姿态调整的理论基础。定位系统利用传感器对环境的感知信息，进行地图构建和自主定位。测距传感器是最主要的传感器，比较常用的有立体视觉、超声波传感器和光学传感器。本文以激光测距仪为例建立其观测模型。观测量z是环境中某一目标特征相对于测距传感器的位置和方向［12］。轴段初始位置与目标位置的空间位姿如图3 所示，在图中建立表征测距仪观测量与轴段位姿关系的观测模型为

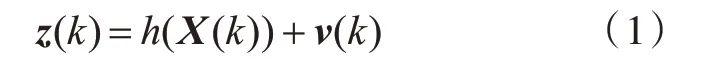
式中：z(k)为k时刻观测量；h(X(k))为观测系统的函数表达式；v(k)为观测噪声，通常指环境中的干扰噪声和模型及传感器本身的误差。以相对于环境特征的方位和环境特征的全局坐标为观测量分别建立观测方程。

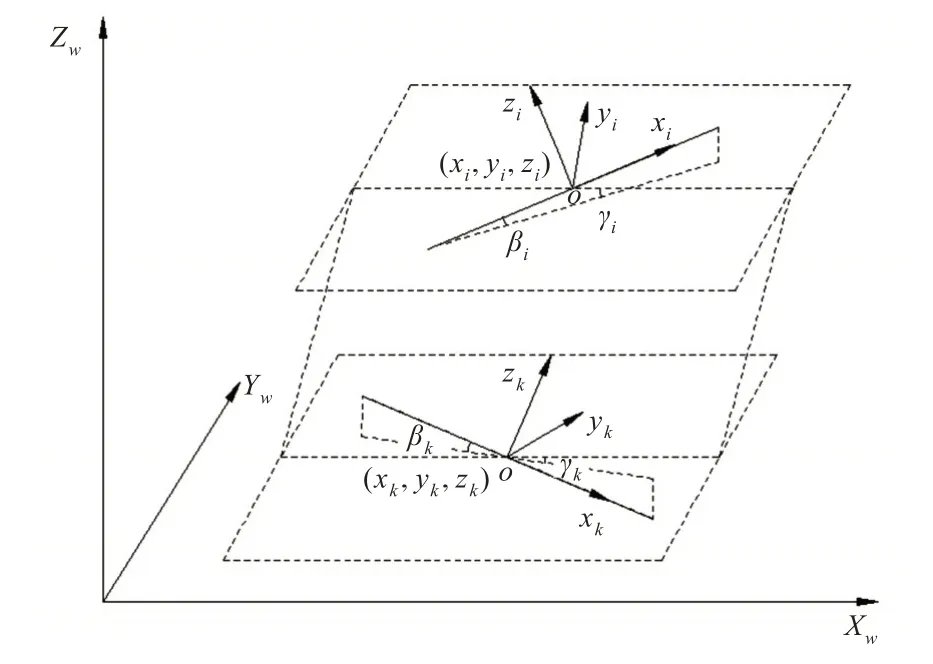
图3 轴段空间位姿Fig.3 Spatial attitude of the shafting

对于测距传感器，通常用目标特征相对于传感器的距离ρ(k)和方向φ(k)=(β(k)，γ(k))T来表示观测量。假设运动机构传感器的当前位置为Xs(k)=(xs，ys，zs，βs，γs)T，轴段的当前位置可表示为X(k)=(xk，yk，zk，βk，γk)T，某个目标特征的位置为Xi=(xi，yi，zi，βi，γi)T，那么定位系统传感器对于目标特征的位姿观测模型为

传感器通常用极坐标表示观测信息，经坐标变换将其变换为笛卡尔坐标，进而可以得到以目标特征的全局坐标作为观测量的观测方程。假设轴段的当前位置为X(k)，在自主定位平台的坐标系为O-xk yk zk，某一目标特征的坐标为Xl=(xl，yl，zl)T，在全局坐标系中观测量的坐标为Xw(k)=(xw，yw，zw)T，则全局系统的观测模型为

3 轴段定位方法

若要使轴段在所设计的运动机构的支撑下到达目标位置并与基准轴对齐，那么对轴段中心线的确定非常关键。本节拟采用三边质心定位算法，通过在轴系外端面布置3 个定位传感器来实现对轴段中心线的确定。三边质心定位算法是三边测量法和质心算法的结合。三边测量法是一种基于距离的定位算法。在传感器网络中节点通常可以分为信标节点和未知节点。信标节点是位置信息已知的节点，一般所占比例很小，通常通过手工配置或者配备GPS接收器来获取自身的位置信息［13］。

设未知节点坐标P（x，y），已知3 个信标节点坐标分别为A（xa，ya），B（xb，yb），C（xc，yc），它们到P的距离分别为da，db，dc。分别以A，B，C 为圆心，da，db，dc为半径画圆，理想情况下3 个圆相交于一点，如图4 所示。

在三边测量法中可由如下方程求得未知节点P 的坐标

图4 三边测量法示意图Fig.4 Schematic diagram of the trilateration method

质心算法基于2 个假设条件：射频信号的传播遵循理想的圆球模型；节点的通信半径相同且不会改变［14］。该算法利用了计算几何中质心的思想，假设n 边形的顶点坐标分别为(x1，y1) ，(x2，y2)，…(xn，yn)，设其质心坐标为（x，y），则有

信标节点周期性地广播包含自身位置信息的消息，在时间t 内未知节点收到来自信标节点i 的消息数目为Nr（i，t），而信标节点i发出的消息数目为Ns（i，t），可以得到信标节点与未知节点的连通指标

如果C大于设定的阈值，则认为未知节点处于信标节点i 的覆盖区域内，即与信标节点i 连通。这样对于每个未知节点都可以选出与其连通的所有信标节点，然后把这些信标节点的质心作为该未知节点的坐标。

在实际操作中，外端面布置有3 个定位传感器的轴段处于由若干信标节点组成的局部传感器网络中，3 个定位传感器的位置通过上述三边质心定位算法分别得到，进而可利用这3 点求出轴段中心线的位置信息。

4 工作空间分析

4.1 支撑点位置条件

分析轴段的旋转过程可以发现，旋转角越大，支撑点距离轴段两端点越近，因此若初始支撑点布置不当，轴段有从平台坠落的风险。如图5 所示。在XY 平面，轴段在A，B 位置旋转，支撑点过F，G 点时有最大旋转角α，此时运动机构初始支撑点P，Q 之间的距离为

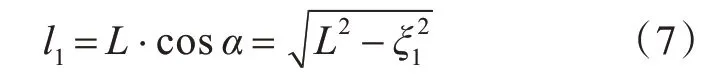
式中：L为轴长；ξ1为G，H 之间的距离。

图5 XY 平面支撑点位置条件Fig.5 Position conditions of the support points in XY plane

在图6 的XZ 平面中，出于安全性考虑，轴段最大旋转角为不发生滑移的最大倾斜角β，此时运动机构初始支撑点P，Q 之间的距离

图6 XZ 平面支撑点位置条件Fig.6 Position conditions of the support points in XZ plane

由于β＜α，故l1＜l2，那么初始状态下运动机构支撑点之间的距离δ应满足的条件为δ＜l1，即

4.2 图解法分析工作空间

在利用平台对轴段进行定位的过程中，轴段的空间姿态是通过2 个三自由度运动机构的同步运动实现的［15］。在图3 所示的参考坐标系中，轴沿X，Y 和Z 方向的平动通过一对直线导轨（电动缸）的同向同步运动实现，并通过直线导轨（电动缸）的反向同步运动实现其绕中心点的转动。

基于图解法分析轴段的工作空间，需要求取轴段所能达到的极限位姿。轴段的空间运动是沿X，Y，Z 方向的平移和绕Y，Z 轴旋转运动的组合，因此其末端可达的区域是由一系列圆弧及直线组合而成的区域，即极限位姿边界曲线。为便于实现轴段的定位作业，轴段的初始姿态位于中位，即运动机构的电动缸和直线导轨都处于各自行程的中间位置。

在XY 平面中，A，B 是轴段两端点的初始位置，P，Q 为运动机构支撑点的位置。轴段可在运动机构的驱动下在行程范围内沿Y 方向平移，Y 方向行程为ξ2，如图7 所示。A1B1是轴段在Y 轴正向平移的极限位置。轴段也可绕轴段中心点转动，如轴段平移至A2B2位置时，轴段绕中点转动，但受到直线导轨行程的限制，支撑点的极限位置为G 点，即轴段在该处的旋转极限位置为A3B3。同理，可得轴段右端点的极限位姿边界曲线。由于机构及轴段运动的对称性，可以得到在XY 平面中不考虑轴段沿X 方向平移时的运动空间［16］。

图7 XY 平面轴段位姿图Fig.7 Spatial attitude of the shafting in XY plane

在XZ 平面中，A，B 是轴段两端点的初始位置，P，Q 为运动机构支撑点的位置。轴段可在运动机构的驱动下在行程范围内沿Z 方向平移，Z 方向行程为ξ3，如图8 所示。A3B3是轴段在X 轴正向平移的极限位置。由于X，Z 平面是空间的竖直面，而轴段是否发生滑移取决于静摩擦力的大小，与其倾斜角有关。

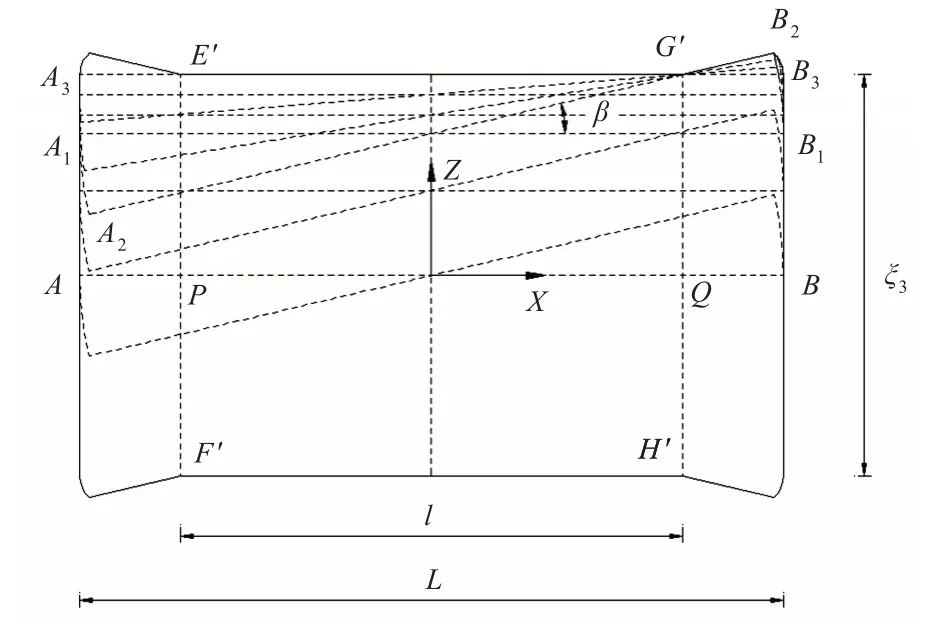
图8 XZ 平面轴段位姿图Fig.8 Spatial attitude of the shafting in XZ plane

设轴段与运动机构支撑件之间的静摩擦系数为fs，则轴段不发生滑移的最大倾斜角为

当轴段平移至A1B1位置时，轴段的最大倾斜位姿过支撑点的极限位置G′，即轴段在该处的旋转极限位置为A2B2。这样，轴段的平移位置在AB和A1B1之间时，可达最大旋转角β，而在A1B1和A3B3之间，最大旋转角则小于β，轴段的右端点在B2B3之间划出一条曲线。由于机构及轴段运动的对称性，可以得到在YZ 平面中，不考虑轴段沿X方向平移时的运动空间。

事实上，在上述两平面内，轴段分别可沿Y，X轴在ξ2，ξ1行程内平移，则实际的工作平面需要做相应延伸，但边界曲线部分依然为上述分析结果。

5 结 语

本文工作主要在已设计的用于轴段智能安装的六自由度并联式平台基础上展开，建立了基于传感器的观测模型，利用三边质心定位算法对轴段进行定位，基于安全考虑，计算了支撑点的位置许可范围，通过分析平台各种工况极限位置条件得到了轴段工作空间。据此可预估轴段安装现场工作空间的安全性，有效避免装配作业时不必要的损坏。本文工作旨在为进一步的研究工作及工程应用提供理论指导和技术支持。