单矢量水听器的高分辨方位估计应用研究

梁国龙，张锴，付进，张瑶，李利

(哈尔滨工程大学 水声技术重点实验室，黑龙江 哈尔滨150001)

0 引言

矢量水听器可以同时、共点测量声场的声压与振速，比传统的声压水听器获得更多的声场信息，依靠单个矢量水听器就可以完成水下目标的方位估计，因而它的应用受到越来越多地重视。近年来，国内外关于单矢量水听器应用方面发表了很多文章，如Nehorai 给出了基于声强流矢量分解和基于速度协方差矩阵分解的两种方位估计算法，杨士莪提出了利用宽带声压与振速的偶次阶矩所组成的联立方程组求解目标的方位和能量等［1-4］。同时，矢量水听器阵列信号处理方面也取得很多成果，如Hwakes建立了有关矢量水听器阵列的方位测量模型，K.T.Wong 和M.D.Zoltowski 提出了基于电磁矢量传感器和水声质点速度水听器的自初始化MUSIC 算法等［5-10］。目前单矢量水听器的方位估计都是基于声能流的最大似然估计，而高分辨方位估计算法又都是建立在基于空间分布阵列模型的基础之上，而且针对宽带信号的处理还要建立起相应的频域模型，并且在模型失配的情况下高分辨方位估计性能还会严重的恶化［11-12］。考虑到单矢量水听器本身就具有阵列流型的特点，将阵列信号处理中的子空间分解理论应用到该矩阵流型上，给出一种基于MUSIC 的单矢量水听器高分辨方位估计算法。该算法在实现对窄带信号和宽带信号高分辨方位估计的同时却不需要建立信号处理的频域模型，而且，由于是基于矢量水听器本身具有的3 ×1 维阵列流型，不存在传统MUSIC 算法中阵列校准的问题，使得单矢量水听器不仅具有以往只有在阵列信号处理中才能拥有的高分辨方位估计能力，还易于工程上的实现，为高分辨方位估计算法在单矢量水听器的应用奠定了基础。特别指出的是，当采用矢量水听器4×1 维阵列流型时，还可同时估计目标的水平角和俯仰角。

1 单矢量水听器高分辨方位估计原理

1.1 MUSIC 算法基本原理

在理想情况下，N 个远场窄带信号入射到空间M 元的阵列上，阵列接收窄带远场信号的波达方向(DOA)数学模型为

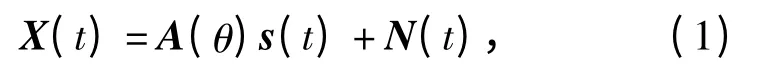
式中:A(θ)是空间阵列的M ×N 维流型矩阵;X(t)是阵列的M×1 快拍数据矢量;s(t)是空间信号的N×1 维矢量;N(t)是阵列的M×1 维噪声数据矢量。则阵列数据的协方差R 可以分为与信号、噪声相关的两部分，即

其中，“H”表示取共轭。此时的信号子空间与入射信号的导向矢量张成的空间是同一个空间，在理想条件下，数据的信号子空间与噪声子空间正交，即入射信号的导向矢量与噪声子空间正交。经典的MUSIC 正是基于上述性质提出的，而实际上对R 进行特征分解计算得到的噪声子空间特征矢量和导向矢量a(θ)并不能完全正交，因此实际上求DOA 是以最小化搜索实现的，即

则空间谱P(θ)的表达式为

现有的大部分高分辨方位估计算法都是以预知信源数为前提的，一般做法是先估计信源数目，再估计方位。本文中信源的数目假定已知。

1.2 单矢量水听器的阵列流型

本文仅考虑二维问题，即矢量水听器输出同点的声压p 和正交的二维振速vx，vy，则测量的方程可以表示为

式中:x(t)为水听器接收的声压波形;θ 为入射声波的水平方位角，θ 的取值范围为-π ＜θ ＜π.本文所介绍的基于单矢量水听器的MUSIC 算法不同于传统的MUSIC 算法，它充分利用了矢量水听器自身阵列流形特性。假设目标信号是由N 个不同频率的单色水下声波构成，传播介质各向同性，则该信号入射到矢量水听器上，其第k 个水声信号在矢量水听器上的阵列流型a(θk)表达式如下

其中，“T”表示取转置。a(θk)的第1 和第2 个分量对应于矢量水听器两个振速通道输出，最后一个分量对应于矢量水听器声压通道输出。

矢量水听器的阵列流型有以下特点:1)一个矢量水听器可测量得到一个3 ×1 维的流型矢量，即单矢量水听器本身可等效为一个三分量的阵列。2)不同于传统的空间分布阵列，单矢量水听器阵列流型中并没有包含时间延迟的信息。这种矢量水听器的阵列流型只包含目标的方位信息，与到达信号的频率无关，故不会产生传统方位估计中的频率模糊问题。3)无论源参数如何变化，任意源信号的流型矢量，前两个分量的范数之和总是与最后一个分量相等，且等于1.

1.3 基于MUSIC 算法的单矢量水听器方位估计

首先通过采样接收三路数据产生一个3 ×L 维的矢量水听器阵列矩阵X(t)，L 是数据采样点数，在这里，X(t)满足(1)式接收数据模型，此时A(θ)为3 ×L 维的流型矩阵，其表达式为

其中，a(θk)即为(5)式所示的第k 个水声信号的单矢量水听器阵列流型。将单矢量水听器接收数据X(t)的协方差矩阵R 进行特征分解，并假定UN是其特征分解后小特征值对应的特征矢量张成的空间，此时构造入射信号的导向矢量a(θ)如下

显然，若导向矢量a(θ)指向信号子空间时，其必与噪声子空间UN正交，则利用(4)式即可得到单矢量水听器MUSIC 算法的空间谱估计表达式。与经典MUSIC 算法一样，本方法也需要进行空间谱搜索。在算法实现时，将待搜索的范围分成等间距的单位Δθ 进行方位谱搜索。因此得到估计的精度也与搜索步长Δθ 有关，在足够的信噪比条件下，Δθ 越小，精度越高。

2 计算机仿真分析

2.1 窄带信号的方位估计

仿真中噪声为带宽2 000 Hz 的零均值高斯噪声，信号为2 000 Hz 的单频信号，样本时间2 s，采样频率4 000 Hz，方位角θ=30°，搜索步长Δθ=0.1°，计算结果为100 次独立实验的统计数据，如无特别说明上述仿真条件不变。

图1示出不同信噪比(SNR)情况下方位估计的性能曲线。为了进行比较，同时给出了互谱法的方位估计结果。可以看出，在谱级SNR 大于35 dB 时，两种方法的方位估计偏差都在1°以内，说明在高SNR 情况下，该算法的估计是无偏估计。

图1 不同信噪比下窄带信号方位估计性能Fig.1 The performance of DOA estimation of narrowband signal to SNR

需要指出，该方法得到的方位估计标准差还与搜索步长有关。当搜索步长较大时，尽管方位估计标准差很小，但却是有偏估计。因此，在足够高的SNR 条件下，搜索步长越小，方位估计精度越高，可以达到无偏估计。

2.2 宽带信号的方位估计

仿真中信号和噪声均为带宽2 kHz 的零均值高斯噪声，样本时间2 s，采样频率4 kHz，方位角θ=30°，搜索步长Δθ=0.1°，计算结果为100 次独立实验的统计数据，如无特别说明上述仿真条件不变。

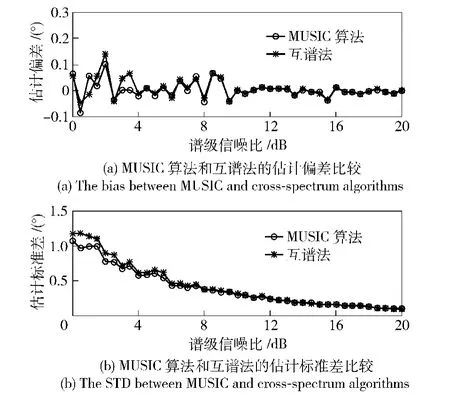
图2 不同信噪比下宽带信号方位估计性能Fig.2 The performance of DOA estimation of wideband signal to SNR

观察图2可以发现，该算法对宽带信号和窄带信号的方位估计性能具有类似的性质，这里不再赘述。需要指出，传统的宽带信号阵列处理需要建立相应的频域模型，或是采用非相干信号子空间方法，即将宽带信号在频域上分成若干窄带信号，利用窄带的DOA 估计方法估计方位，或是采用相干信号子空间方法，通过聚焦变换，将所有子带的能量映射到某一频段上，再参考窄带的DOA 估计方法估计方位。而本算法对宽带信号和窄带信号的处理都是基于时域模型的基础之上，不需要建立相应的频域模型，这也是该算法的优势之一。

3 湖试数据分析

3.1 湖试数据处理

为了验证算法的有效性，处理了湖上实验数据。实验中目标信号为宽带高斯噪声，信号发射时接收信噪比很高，可近似看作纯目标信号，不发射时采集的数据为纯干扰数据。信号所占频带500～5 500 Hz，采样频率16 kHz.

图3示出了处理2 s 湖试数据得到的方位谱，为了具有对比性，同时给出了同一段数据的互谱直方图。由于在实际应用中单矢量水听器声压、振速通道幅相特性会存在不一致的情况。此时算法的空间谱分辨性能会严重褪化，特别是当声压幅度远小于振速幅度时，空间谱中可能会产生"伪峰"。在这里可以通过采用声压振速通道功率归一化技术来优化空间谱估计的性能。

图3 两种算法处理湖试数据得到的空间谱Fig.3 The chat of spatial spectrum given by data on lake after MUSIC and cross spectrum bar graph algorithms processing

对估计结果进行了比较分析发现，互谱法方位估计得到的结果是70.329 2°，而MUSIC 算法的方位估计得到的结果是70.9°，两种算法处理得到的估计方位十分接近，数据处理结果验证了算法的有效性。

3.2 改进MUSIC 算法

如图3中所示，互谱直方图的方位谱中目标真实方位的反方向附近存在另一个谱峰，而这种反方向的“能量泄露”相当于增加了额外的声源数目。考虑到这种情况，本文给出了一种基于改进MUSIC算法。算法步骤如下:1)首先采用MUSIC 算法对目标方位进行粗测。为减小计算量，搜索步长 取值可以较大，通过确定方位谱中峰值的位置得到目标所在的大致方位范围;2)考虑到增加的额外声源，修正数据协方差矩阵特征分解得到的噪声子空间，将此时信源数目由一个判定为两个，从而得到新的噪声子空间;3)基于噪声子空间 得到改进MUSIC 算法的空间谱。为了提高精度，可在 范围内采用小搜索步长进行角度搜索。

图4示出了改进算法的空间方位谱。由图可知，相较与MUSIC 算法，改进MUSIC 算法的空间谱图在目标方位处的谱峰宽度更窄，方位分辨力更高。此时改进算法得到的方位估计结果是71.1°，与MUSIC 算法结果70.9°非常接近。

图4 改进算法处理湖试数据得到的空间谱Fig.4 Performance of spatial spectrum given by data on lake after improved algorithm processing compared with conventional algorithm

图5～7 示出了处理一段20 s 湖试数据得到的瀑布图，通过对比发现，改进算法给出的目标时间方位历程更加清晰，湖试数据的处理结果充分地验证了改进算法的有效性。由于算法采用了空间谱峰值搜索的策略，因此算法的估计精度受到搜索步长的制约，可以采用Root-MUSIC 算法代替空间谱搜索，提高方位估计精度和实时处理速度。

图5 改进MUSIC 算法处理湖试数据得到的瀑布图Fig.5 The chat of waterfall given by data on lake after improved MUSIC algorithm processing

4 结论

本文介绍了一种单矢量水听器方位估计新方法，该算法结合矢量水听器自身的阵列流型特点，将阵列信号处理中的MUSIC 算法应用到单矢量水听器上。仿真结果表明，在不需建立频域模型情况下，该算法仅用单个矢量水听器就实现了窄带信号和宽带信号的高分辨方位估计。进一步分析表明，在足够高的SNR 条件下，该算法可以得到高精度的渐进无偏估计。湖试数据的处理结果验证了该算法的有效性，针对实际矢量水听器的工作环境，给出了相应的改进算法。考虑到算法基于单矢量水听器本身具有的3 ×1 维阵列流型，不存在传统MUSIC 算法中阵列校准的问题，具有一定的工程应用价值。

图6 MUSIC 算法处理湖试数据得到的瀑布图Fig.6 The chat of waterfall given by the result of data on lake after MUSIC algorithms processing

图7 互谱直方图处理湖试数据得到的瀑布图Fig.7 The chat of waterfall given by data on lake after Cross Spectrum algorithms bar graph processing

References)

［1］ Nehorai A，Paldi E.Acoustic vector sensor array processing［J］.IEEE Trans on Signal Processing，1994，42(9):2481-2491.

［2］ 杨士莪.单矢量传感器多目标分辨的一种方法［J］.哈尔滨工程大学学报，2003，24(6):591-595.YANG Shi-e.Method of multi-source distinguish-ing by single vecor transducer［J］.Journal of Harbin Engineering University，2003，24(6):591-595.(in Chinese)

［3］ 王逸林.应用希尔伯特黄变换的单矢量传感器多目标分辨研究［J］.声学技术，2006，(4):376-380.WANG Yi-lin.Separation of multiple targets using a single vector sensor based on Hilbert-Huang transform［J］.Technical coustics，2006，(4):376-380.(in Chinese)

［4］ 姚直象，惠俊英，王德俊，等.基于DEMON 线谱的单矢量水听器双目标分辨［J］.应用声学，2005，24(3):171-176.YAO Zhi-xiang，HUI Jun-ying，WANG De-jun，et al.Identify two targets by a single vector hydrophone based on DEMON spectrum［J］.Applied Coustic，2005，24(3):171-176.(in Chinese)

［5］ Hwakes M，Arye Nehorai.Effect of sensor placement on acoustic vector-sensor array performance［J］.Journal Oceanic Engineering，1999，24(1):33-404.

［6］ Wong K T，Michael.Self-initiating music-based direction finding in underwater acoustic particle velocity-field beam space［J］.IEEE Journal Oceanic Engineering，2000，25(2):262-273.

［7］ 徐海东，梁国龙，等.解析声能流Capon 空间谱估计［J］.声学技术，2004，(3):178-192.XU Hai-dong，LIANG Guo-long.Capon spatial spectrum estimation based on analytic acoustic energy fiux［J］.Technical Coustics，2004，(3):178-192.(in Chinese)

［8］ 白兴宇，杨德森.基于声压振速联合信息处理的声矢量阵相干信号子空间方法［J］.声学学报，2006，(5):410-416.BAI Xing-yu，YANG De-sen.The coherent signal subspace method based on combined information processing of pressure and particle velocity using the acoustic vector sensor array［J］.Acta Acoustic，2006，(5):410-416.(in Chinese)

［9］ 王海陆.基于声矢量传感器阵的相干源高分辨方位估计［J］.舰船科学技术，2007，(7):71-73.WANG Hai-lu.High-resolution DOA estimation of coherent sources based on acoustic vector-sensor array［J］.Ship Science and Technology，2007，(7):71-73.(in Chinese)

［10］ 姚直象.基于多重信号分类法的一种声矢量阵方位估计算法［J］.声学学报，2008，(4):305-309.YAO Zhi-xiang.A bearing estimation algorithm using an acoustic vector-sensor array based on MUSIC［J］.Acta Acoustic，2008，(4):305-309.(in Chinese)

［11］ 王永良.空间谱估计理论与算法［M］.北京:清华大学出版社，2004:91-93.WANG Yong-liang.The theory and arithmetic of spatial spectrum［M］.Beijing:Tsinghua University Press，2004:91-93.(in Chinese)

［12］ 王鼎.幅相误差对MUSIC 算法空域谱及分辨性能影响的分析［J］.通信学报，2010，(4):55-63.WANG Ding.Analysis of the effects of the amplitude-phase errors on spatial spectrum and resolving performance of the MUSIC algorithm［J］.Journal on Communications，2010，(4):55-63.(in Chinese)