舰载武器垂直装填机械防摇控制研究

瞿军，马大为，刘为

(1.南京理工大学 机械工程学院，江苏 南京210094;2.海军航空工程学院 飞行器工程系，山东 烟台264001;3.92214 部队，浙江 宁波315826)

舰载垂直装填机械是舰载武器垂直发射系统的一种多关节、可伸缩折叠式特种起重机，用于舰载武器的装填作业。由于海浪作用以及吊重与装填机械臂末端是通过柔性钢缆连接，不可避免地会产生摆动。这种摆动对装填的工作效率和作业安全都会产生很大的危害，直接影响装填的快速性。因此，如何消除武器在装填过程中的摆动是提高武器装填效率，实现海上快速补给的关键技术之一。

针对港口起重机、船用起重机等机械设备的防摇控制，国内外已经有较多的研究。如Khalid［1］采用输入脉冲控制器来消除桥式吊车负载摆动;王伟、易建强等［2］将分级滑模控制应用于桥式吊车系统;刘德君、张兴华等［3］采用自抗扰控制器对桥式吊车系统进行定位和防摆控制。但一般都是针对某一特定设备、或特定环境，如有的只研究起重机运输的快速性，而忽略了现场的安全性;有的只研究起重机的抗摆控制，而忽略了外界的干扰(如船用起重机所受的风和浪等影响等)。

舰载垂直装填机械需要在海上作业，考虑舰艇摇摆和海上风浪的影响对其防摇控制是至关重要的。此外，舰载垂直装填机械属于欠驱动系统，要想通过一个驱动关节的运动来同时实现回转运动、抗负载摆动和抗外界干扰，通常是困难的。滑模控制具有对外界扰动不变性等特点，并且可应用于欠驱动系统，因此滑模控制适合于实现舰载垂直装填机械的防摇控制。文献［4］提出了一种具有双层滑模面结构的滑模控制方法，将其应用于桥式吊车这类典型欠驱动系统，实现了水平距离和摆角的同时控制。但该方法只研究了二自由度欠驱动系统的情况，且没有考虑消除滑模控制“抖振”的问题。

本文提出一种适用于三自由度欠驱动系统的分层模糊滑模控制方法，该方法在保证系统稳定的前提下，使舰载垂直装填机械运动到目标位置的同时，实现吊重空间摆角的减小。

1 系统数学模型

在结构原理上，舰载垂直装填机械是起重机与工业机器人的结合体，可以用机器人动力学建模原理进行建模。文献［5］中将舰载垂直装填机械看作开链式机械手系统，如图1所示。

图1 舰载垂直装填机械的机械手模型Fig.1 Robotic operator model of ship-borne vertical loader

图1中，将舰载垂直装填机械等效为具有5 个杆件的开链式机器人机械手系统，杆件之间通过回转关节连接。其中，虚拟杆件1 可看作从舰船横摇摇心到装填机机座的虚拟杆，关节变量为θ1，即横摇角;装填机回转臂关节变量θ2为平台回转角度;起重臂关节变量θ3为吊臂的俯仰角度;悬吊钢缆和吊重为描述吊重的空间运动，引入质量和长度均为零的虚拟杆件2，利用虚拟关节的关节变量θ4、θ5及悬吊钢缆长度来描述吊重相对于吊顶的空间位置。

运用牛顿—欧拉递推法得到舰载垂直装填机械的动力学模型为

式中:ci=cosθi;si=sinθi;cφ=cosφ;sφ=sinφ，i=1，2，…，5，(以下同)。φ 为吊重的径向摆角;θ5为吊重的切向摆角;τ2为回转关节驱动力矩，其余参数意义见文献［5］。

方程(1)、(2)、(3)较为准确地反映了舰载垂直装填机械进行回转作业时吊重的运动状态，较直观地描述了吊重的空间摆角与舰载垂直装填机械回转关节驱动力矩之间的动力学关系，并且包含了舰艇摇摆和风载荷的影响。

2 防摇控制器设计

2.1 系统模型优化及控制系统结构

为便于控制器的设计，首先应用部分反馈线性化方法对系统模型进行优化。若令

其中，U 为新的控制输入。

因为c23m3r2c3≠0，所以将(4)式代入(1)式可得

这样，系统的输入变量由回转关节的驱动力矩转换成了回转关节的回转角加速度

选择系统的状态变量为x1=θ2，x2=，x3=φ，x4=，x5=θ5，x6=，输入变量为U;则方程(1)、(2)、(5)可写成状态空间方程组形式为

其中:

显然，(6)式为一类典型的三自由度单输入的欠驱动非线性系统。

根据系统模型设计的控制系统结构如图2所示。图中，期望位置输入信息qd，q·d主要包括:舰载垂直装填机械回转运动的期望角度和初始角速度，切向摆角和径向摆角的期望角度和角速度。输入信息经过负反馈后输入到防摇控制器，在防摇控制器中通过控制算法得到防摇控制量(此处为回转角的角加速度)，控制量经过部分反馈线性化补偿后转换为关节驱动力矩，从而控制舰载垂直装填机械的运动。

图2 控制系统结构图Fig.2 Schematic diagram of the anti-swing controller system

2.2 分层滑模控制器设计

分层滑模控制思想就是将整个系统分成多个子系统进行研究，这样，对于每个子系统而言则可以按照常规的滑模函数的选取方法进行设计，从而将整个系统的问题降级为各个子系统的滑模函数设计的问题，最后再将各个子系统连接在一起。

设舰载垂直装填机械回转运动的期望角度为θ2r，期望角速度为，切向摆角和径向摆角的期望角度和角速度均为零。令e1=x1-θ2r，e2=x2-，则各层滑模面构造为

式中:系统跟踪误差Ei=［e1，x3，x4，x5，x6］;Si=［e2，s1，s2，s3，s4］;ci为各滑模面斜率，正常数，i=1，2，…，5.

定义一组Lyapunov 函数

这里可以发现，如果选择滑模系数满足cixi+1·si-1＞0，i=2，…，5，可以得到

定义滑模系数按如下形式选取

其中，Ci为正常数。因为有si=cixi+1+si-1和cixi+1·si-1＞0 可以看出si和si-1是同号的，因此上式就变成

以下将推导滑模控制量来保证最后一层滑模平面能够收敛到零。

设总的滑模控制量为

其中，ueq为等效控制量，usw为切换控制量。由此可得

若令

以及

则有

其中，k 和η 为常数。

将(15)式和(16)式代入(13)式即可得到总的控制律

由(17)式及(9)式可知，采用(18)式所示控制律，不仅使最后一层滑模面满足了Lyapunov 稳定性判据，其他各层滑模面也满足了Lyapunov 稳定性判据，即能使所有滑模面均稳定并收敛到零。

2.3 系统参数的模糊调节方法

滑模控制中的“抖振”现象影响控制系统性能。在保证系统稳定的前提下，通过对参数进行模糊调节的方法来消除系统的“抖振”。

1)滑模面斜率ci的模糊调节方法

滑模面的斜率ci是影响控制系统动态性能的主要因素:随着滑模面斜率的减小，上升时间增大，超调量减小，调整时间减小，同时闭环稳定性增强;反之，上升时间减小，超调量增加，调整时间增加，闭环稳定性减弱。因此，可得到ci的模糊调节原理为:当系统跟踪误差Ei较大时，增大ci，使系统以最快速度接近滑模面和平衡点;反之，减小ci，以减小误差变化率，抑制超调和缩短调节时间。为保证系统稳定性，需限定滑模面斜率的调节范围，设

式中:Ci为ci的基本值;Bi为ci的变化范围;λi为调节量，可由以下模糊推理获得

其中，Ri为m 条规则中第i 条，Ai为输入变量|Ei|的模糊集，yi为输出变量的模糊集。输出采用单值隶属函数，重心法解模糊输出

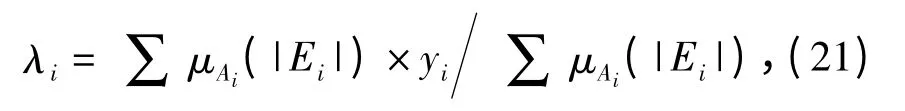
其中，μAi(|Ei|)为第i 条规则的激活强度。

2)切换控制量的模糊调节方法

因为切换控制量usw与滑模函数s5有关，是产生抖振的主要原因之一，因此，通过调节切换量的参数来消除系统的抖振具有很大意义。

将(15)式写成如下形式

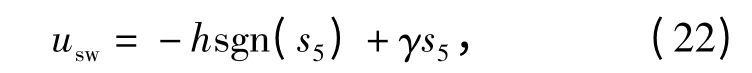
由分析可知，h 过小将影响非滑模到滑模模态的过渡时间或难以满足可达性条件;h 过大，将导致大的抖振。考虑参数不确定性，在仅知道参数上下界的情况下，会使h 取值过大，不可避免产生大的抖振。h 的模糊调节原理为:因为一个大的切换增益将迫使状态轨迹迅速地接近滑模超面s5=0，但同时会产生抖振，所以当状态轨迹远离滑模超面时，即当|s5|大时，增大h;反之，当|s5|小时，减小h.当状态轨迹偏离滑模超面(s＞0)时，如果|5|大，增大h以迫使状态轨迹返回，反之亦然。当状态轨迹接近滑模超面时，即s＜0，如果|5|大，减小h，以减小抖振，反之亦然。

h 的模糊取值规则如下

其中，Ri为m 条规则中第i 条，Bi，Ci表示模糊集，zi为输出变量的模糊集，则规则集输出h 与模糊规则之间可以通过模糊推理建立如下关系

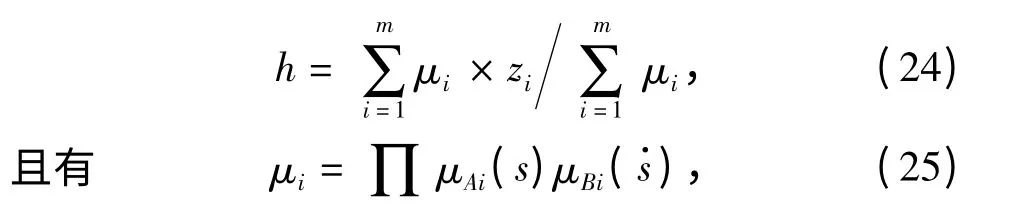
其中，μAi(s)，μBi(s)是s，的隶属度函数。

2.4 模糊控制器设计

1)各层滑模面模糊控制器设计

由于各层滑模面都有相似的调节原理，为了减小系统的复杂程度，各层滑模面采用相同的模糊推理规则。对输入Ei和输出λi均取模糊集为NB，负大;NM，负中;NS，负小;ZO，零;PS，正小;PM，正中;PB，正大。其隶属度函数均采用三角型隶属度函数。其模糊控制规则如表1所示。

表1 滑模面的模糊控制规则Tab.1 The fuzzy control rules of the sliding face

2)切换控制量模糊控制器设计

对输入s5、5和输出h 均取模糊集为NB，负大;NS，负小;ZO，零;PS ，正小;PB，正大。其隶属度函数均采用三角型隶属度函数。其模糊规则如表2所示。

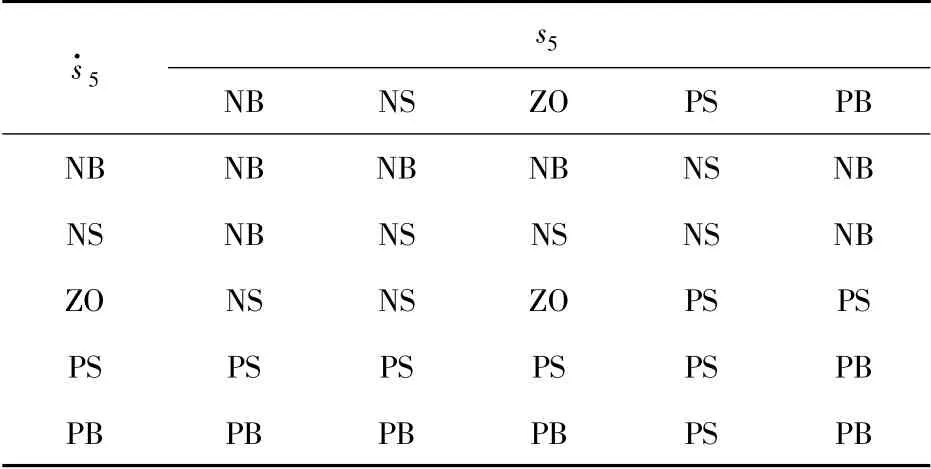
表2 切换控制量的模糊控制规则Tab.2 The fuzzy control rules of the changing controlled variable

设置仿真条件为舰载垂直装填机械的回转运动过程，假定回转运动初始条件为回转角及吊重径向摆角和切向摆角的初始角度θ2=φ=θ7=0°;初始角速度===0°/s.选取回转运动所要求到达的期望回转角θ2d=120°，吊重摆角的期望值为φd=θ7d=0°，回转角及摆角的期望角速度为===0°/s.选取五级海情，采用文献［6］中的舰载垂直装填机械及各级海情下舰艇的摇摆值和风载荷的参数值。

由试凑法得到参数:C1=C4=C5=0.1，C2=C3=0.2，B1=B4=B5=1，B2=B3=1.2，γ=2.5.

采用Matlab/Simulink 仿真，结果如图3～图7所示。

由图3可以看出，在控制器的作用下舰载垂直装填机械能在50 s 左右到达装填目标位置并稳定。

由图4和图5可以看出，当没有对参数进行模糊调节时，各层滑模面虽然能保持稳定，但存在明显的“抖振”现象;而对参数进行模糊调节后，各层滑面的“抖振”现象被消除。

由图6和图7同样可以看出对参数进行模糊调节后控制变量的“抖振”现象被明显消除。

由图8和图9可看出，采用分层模糊滑模控制后，与不加控制时相比，吊重的径向摆角和切向摆角显著减小，均减小到了5°以内，达到了防摇控制的目标。

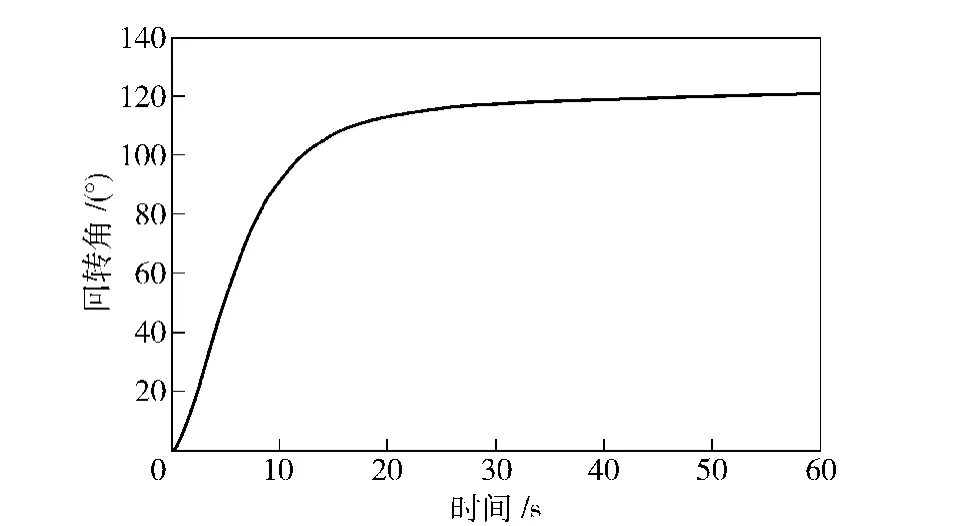
图3 回转角变化曲线Fig.3 Curve of rotating angle

图4 没有对参数进行模糊调节时的各层滑模面曲线Fig.4 Curve of each sliding face when no fuzzy adjusting

图5 对参数进行模糊调节时的各层滑模面曲线Fig.5 Curve of each sliding face when has fuzzy adjusting

图6 没有对参数进行模糊调节时的控制变量曲线Fig.6 Curve of control variable when no fuzzy adjusting

图7 对参数进行模糊调节时的控制变量曲线Fig.7 Curve of control variable when has fuzzy adjusting

图8 径向摆角曲线Fig.8 Curve of radial swing angle

图9 切向摆角曲线Fig.9 Curve of tangential swing angle

4 结论

针对舰载垂直装填机械防摇控制问题，提出了一种分层滑模控制方法，并利用Lyapunov 稳定性判据进行了稳定性证明。针对滑模控制的“抖振”问题，利用模糊调节原理对滑模参数进行模糊调节以消除系统的“抖振”。仿真研究表明，本文所设计的分层模糊滑模防摇控制器具有良好的动态性能，并能显著减小吊重的空间摆角。

References)

［1］ Khalid A，Singhose W，Huey J，et al.Study of operator behavior，learning，and performance using an input-shaped bridge crane［C］∥International Conference on Control Applications，Taipei:2004.

［2］ 王伟，易建强，赵冬斌，等.桥式吊车系统的分级滑模控制方法［J］.自动化学报，2004，30(5):784-788.WANG Wei，YI Jian-qiang，ZHAO Dong-bin，et al.Hierarchical sliding-mode control method for overhead cranes［J］.Acta Automatica Sinca，2004，30(5):784-788.(in Chinese)

［3］ 刘德君，张兴华，段慧达，等.基于自抗扰观测器控制的起重机防摆定位系统［J］.起重运输机械，2007，(2):60-63.LIU De-jun，ZHANG Xing-hua，DUAN Hui-da，et al.Anti-swing position system of crane based on auto-disturbance resistant controller［J］.Hoisting and Conveying Machinery，2007，(2):60-63.(in Chinese)

［4］ 王伟，易建强，赵冬斌，等.基于滑模方法的桥式吊车系统的抗摆控制［J］.控制与决策，2004，19(9):1013-1016.WANG Wei，YI Jian-qiang，ZHAO Dong-bin，et al.Anti-sway control for overhead cranes based on sliding-mode control method［J］.Control and Decision，2004，19(9):1013-1016.(in Chinese)

［5］ 瞿军，刘为.舰载垂直装填机械动力学建模与仿真研究［J］.系统仿真学报，2009，21(6):1726-1729.QU Jun.LIU Wei.Dynamic modeling and simulation analysis of ship-borne vertical loader machine［J］.Journal of System Simulation，2009，21(6):1726-1729.(in Chinese)

［6］ 张杰，张锐，邹继刚，等.船用特种起重机动机座运动学建模方法研究［C］∥2002年6月第四届国际智能控制与自动化会议，上海，2002:712-716.ZHANG Jie，ZHANG Rui，ZHOU Ji-gang，et al.Study on kinematic modeling of shipborne crane under ship’s movement［C］∥Proceeding of 4th World Congress on Intelligent Control and Automation，Shanghai，2002:712-716.(in Chinese)