高阶近似黎曼解模型在火炮内弹道两相流中的应用研究
程诚,张小兵
(南京理工大学 能源与动力工程学院,江苏 南京210094)
0 引言
火炮内弹道过程是一种典型的伴有化学反应的高温、高压、可压缩瞬态两相流动,其循环过程中存在多种物理强间断问题,如激波、火焰波以及爆轰波等,因此火炮膛内两相气动力过程可以简化成带有非齐次源项的黎曼间断守恒模型[1]。这种黎曼间断的存在成为两相流数值方法应用的难点。
对于内弹道过程的黎曼间断问题,一般无法得到解析解,只能通过数值计算方法求解。早期的Lax-Wendroff 两步差分格式在强间断附近产生较强的震荡,在间断处常常会产生非物理解。在内弹道两相流领域得到了广泛应用的MacCormck 格式在进行两相流数值模拟时也容易产生非物理震荡导致计算中断,所以在方程中必须要加入显式人工粘性以及滤波等方式才保证计算的稳定性,这样必然影响计算的精度。而后来引进的TVD 格式,其将气体—固体两相分开处理,气相使用TVD 格式,固相仍然使用MacCormark 格式[2],这种处理方式不仅给程序的编制带来了很大困难,而且在固相以及气固方程耦合方面存在一定的精度损失。而最近被广泛关注的CE/SE 方法其计算单元以及计算格式相对复杂,计算机时较长,且该“菱形网格”推广到多维(尤其是三维)及高阶问题上时会遇到很多较难解决的问题,特别是在进行高雷诺数流动问题时,其计算结果也不太理想[3]。
Roe 提出了基于近似黎曼解的守恒Roe 格式,该方法不仅延续了Godunov 型格式接触间断处的高分辨率和激波捕捉性能强的特点,而且具有低耗散、高计算稳定性以及计算时间相对较短的优点,是当前计算流体力学领域最受欢迎的格式之一[4]。传统Roe 格式是一种只有1 阶精度的迎风格式,为了提高计算精度以及消除耗散带来的误差,通过引入带有TVD 性质的2 阶修正项,对格式进行高阶重构,可以使其达到2 阶精度[5]。
点火管作为火炮装药结构中极其重要的部分,其管内两相流动物理过程具有典型的高温高压强瞬态间断特点,可用黎曼间断守恒模型描述该过程的物理现象。本文以中心点火管为例,通过高阶近似黎曼重构,获得了两相流模型的高阶近似黎曼离散格式,并通过数值计算描述了点火管内复杂两相流动的物理过程,分析了不同因素对点火管点火性能的影响。
1 两相流数学模型
火炮膛内点火管的燃烧与流动是火药颗粒燃烧产生的气相与未燃颗粒的两相流动过程,根据文献[2]中的假设及物理模型描述,由于固相被考虑成不可压缩模型,故可忽略固相能量方程。点火管内一维两相流质量、动量和能量守恒方程可以描述为

式中U、F、S 分别为守恒矢量、对流项和源项,其具体表达式及相关辅助方程可参见文献[2]。
2 黎曼近似模型
2.1 Roe 格式通量分解
近似黎曼求解与其他方法的区别在于通量的求解上,其通量求解时将方程线性化,然后通过近似Roe 平均,求得各个局部黎曼问题上的通量,从而扩大到整个流场。通过Jacobian 矩阵可以实现对双曲方程的线性化。对(1)式进行Jacobian 转换后得

式中A(U)为Jacobian 矩阵系数
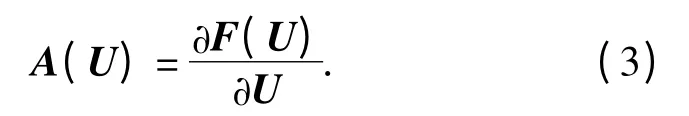
对(1)式进行1 阶Roe 通量离散

式中Fn为控制体单元界面处的数值通量,可定义为

2.2 Roe 平均参数
通常在纯气相中往往使用密度变量ρg作为Roe 平均基本参数,而在对于两相流问题来说,建议采用单位气相质量ρgφg作为基本参数。这样就可以通过Roe 平均化得到平均气相密度、平均气相速度、平均固相速度、平均空隙率等各变量的Roe 平均值。

2.3 熵修正
Roe 格式并不满足Lax 熵稳定条件,容易产生膨胀波问题以及在高马赫数时出现“Carbuncle”现象等非物理现象,从而失去计算稳定性。为了满足熵稳定,一般需要引入额外修正来保证音速膨胀区域的Jacobian 矩阵特征值不为0。熵修正方法的形式较多,对于不同问题的表现性能各异。通过数值比较,本文使用通过改进的Harten-Hyman 型熵修正可以保证足够的计算稳定性[4]。
2.4 高精度格式构造
2.1 节描述的Roe 方法仅有1 阶精度,对于间断问题为了得到更高精度的计算结果,必须引入高阶格式,但高阶项的引入又带来了间断处的数值震荡,所以需要对其使用限制因子,以保证计算精度与计算稳定性。采用通量修正法,1 阶通量形式(5)式可写成如下的2 阶形式:

式中通量限制器采用混合限制器,即对气相密度项使用Superbee 限制器,其余量使用Van Leer 平均限制器[4]。
2.5 源项处理
针对膛内两相流这种带有源项的非线性双曲型守恒系统,一般有两种方法处理:一种是将源项与通量项耦合在一个离散过程中进行求解;另外一种方法是通过时间步分裂法将带有源项的非线性双曲守恒方程分裂成对流项与源项分别求解,对流项使用近似黎曼求解,源项使用常微分方法求解[5]。本文使用后者,该方法可以在保证源项处理精度的基础上,对通量项的求解使用不同类型的格式进行求解,保证了计算的稳定性。
3 数值验证及实验比对
如何保证数值模拟的准确性,不仅需要与实验结果的比对,更需要使用大量已经被广泛认可并带有精确解的经典算例进行数值验证。针对本文这种带有源项的非线性双曲型守恒系统,下文首先应用激波管和源项的经典算例对算法进行数值验证,然后通过点火管算例与实验结果进行了比对,进一步验证数值模拟的正确性。
3.1 激波管算例
激波管问题是进行数值格式验证的经典算例,本文采用的激波管算例总长为2 m,网格数为100,并在x=0 处发生初始间断,左右初值条件分别为:pL=100 000 Pa,ρL=1 kg/m3,uL=0;pR=1 000 Pa,ρR=0.01 kg/m3,uR=0.如图1所示,1 阶、2 阶格式在光滑处都可以与解析解有很好的符合,但是在间断处,1 阶格式出现了明显的过度光滑,抹去了间断处的真实物理信息。而2 阶格式与精确解的符合基本一致,说明了基于Roe 格式的2 阶精度格式是拥有足够计算精度的。

图1 激波管1 阶、2 阶精度与精确解的对比Fig.1 Comparison between the numerical solution and exact solution of shock tube
3.2 源项算例
下面选用Lowe 等[6]首次提出的带有源项的欧拉方程,检验分裂源项方法的计算精度。针对(1)式,将式中各复合变量用下式代替,就构成了一组无粘可压缩纯气相欧拉方程,具体形式为
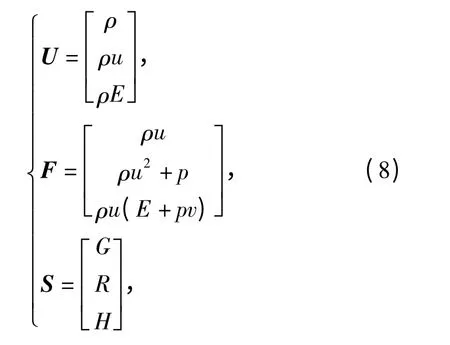
其源项中的各变量选用参见文献[6].
具体的物理模型选取与激波管一样,为了更好捕捉源项的变化过程,将计算区域划分成500 个网格,其初始特征量G0=1 294 301 kg/(m3·s),N=0.1,初始压力p0=10 140 Pa,初始当地声速c0=330 m/s,初始气相速度ug0=0 m/s.
图2所示为气相速度的计算值与精确值的对比,通过与解析解[6]比较发现二者有很好的相似性,其相对误差均小于1%,说明了分裂格式的源项处理在基于2 阶Roe 格式的近似黎曼求解中是值得相信的,并具有相当高的精度。

图2 源项验证的气相速度数值解与精确解对比Fig.2 Comparison between the numerical and analytical solutions of gas velocity for verification of sources
3.3 点火管模型实验验证
本节采用文献[2]中描述的金属点火管物理模型,不考虑点火管内的燃烧流动与火炮膛内过程的相互作用,仅对点火管在一个大气压条件下的两相流动及燃烧过程进行研究。基本初始条件为:点火管长200 mm,在100~200 mm 的管壁上均匀对称分布20 个小孔,气体—固体相速度均为0,初始温度为298 K,压力为一个大气压,破孔压力为20 MPa,其他条件为初始装填条件。点火管两端均为固壁,采用镜面反射法来处理边界[2]。图3给出了点火管1/2 处压力随时间变化的计算结果与实验结果对比,二者的变化趋势一致,计算结果符合较好,说明了近似黎曼数值模拟的准确性。

图3 压力计算曲线与实验对比Fig.3 Comparison between the calculated and measured pressure-time tracts
4 结果与讨论
为了进一步验证高阶黎曼近似模型在火炮两相流应用中的可靠性及稳定性,针对3.3 节所述点火管算例,通过近似黎曼解数值模拟,描述了点火管内复杂两相流动物理过程,并分析了不同因素对点火管点火性能的影响。
4.1 点火管数值计算结果与分析
图4为不同时刻压力分布规律等值线图,其清晰地反映了不同时刻的压力波阵面在点火管内的传播过程。开始阶段点火管左端靠近底火处首先被点燃,而右端还未被点燃,从而形成一右行压力梯度。随着点火波阵面的传播,压力保持稳定上升。当管内压力达到破孔压力后,管内气相与固相颗粒在管内外压力差的作用下喷射到管外,此时管内破孔处会出现压力瞬时骤降,如图4中23.66 MPa 等值线,其出现了很明显的压力震荡。图4中的两条23.66 MPa等值线的对比,可以清晰地反映压力波阵面向右传播后在固壁处反射,右端压力急剧增长的过程。随着流出量的不断增加,压力增长也趋于平缓。当管内流出量大于生成量,管内压力开始逐渐减小,直到全部流完为止。
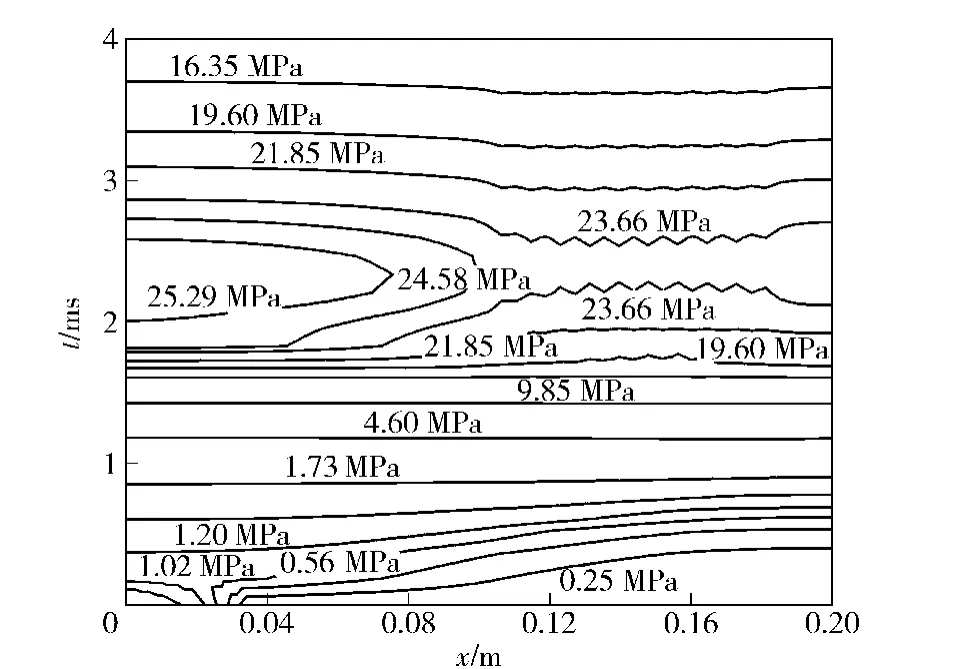
图4 不同时刻压力分布Fig.4 Calculated pressure distribution at x-t
图5为不同时刻管内空隙率分布规律的等值线图。从图中可以看出,开始阶段由于左端首先被点燃产生气体,左端的空隙率不断上升。由于右行压力梯度的作用,结合图7不同时刻的固相速度分布图,可以清晰地看出颗粒在不断地向右端运动,造成了右端颗粒的堆积,空隙率不断下降。而当出现破孔时,由于气相和固相的流出,以及破孔区域的压力震荡会造成管内破孔区域空隙率的紊乱,如图5中空隙率为0.7163 等值线附近的涡旋。当管内压力趋于平缓后,空隙率也在趋于稳定增长。
图6、图7分别为点火管内不同时刻的气相、固相速度分布图。固相速度的分布规律与气相基本一致,但远小于气相速度,这是由于固相颗粒惯性引起的相对运动滞后。未破空前,点火管左端率先被点燃产生气相速度,并带动固相产生固相速度。随着燃烧的进行,右行速度逐渐增加。当压力梯度沿右端壁反射后,在左行压力梯度的作用下,产生图6、图7中的负向速度区域。随着管内火药颗粒的全面着火,燃烧逐渐趋于稳定,管内压力分布也逐渐平缓,此时管内的气相、固相速度分布也逐渐稳定并趋向于0。当管内压力达到破孔压力后,管内物质不断流出,打破了管内速度的平衡,左端以及右端未破孔区域的气相、固相物质分别向破孔区域流动,产生了较大的流动速度。直到燃烧后期,随着流量的逐渐减少,管内流动将会逐渐趋于平缓。
图8为不同时刻破孔区域的流量分布图。从图中可以看出,当破孔出现后,在压力的作用下管内流量迅速增加,然后随着压力的变化,流量开始逐渐减小。结合图4不同时刻压力分布等值线图,当开始破孔时,管内燃气生成量大于流出量,这时管内压力还是处于一个缓慢上升的过程,压力逐渐达到峰值,例如图4中的2.36 ms 处。但随着流出量的不断增加,管内气体生成量已经无法填补由于流出量而造成的压力空白,从而压力开始逐渐下降。
图9为不同时刻颗粒表面温度及点火波阵面的分布图。从图中可以清晰地看出,点火过程中不同时刻不同位置上的火药颗粒表面温度变化情况,以及可以清晰地找到一条点火火焰沿轴向的传播过程曲线,即点火波阵面。从图中可以看出点火波阵面与图4中点火阶段的压力梯度有一定的联系。一般认为,点火阵面处在压力梯度最陡峭的地方[1]。
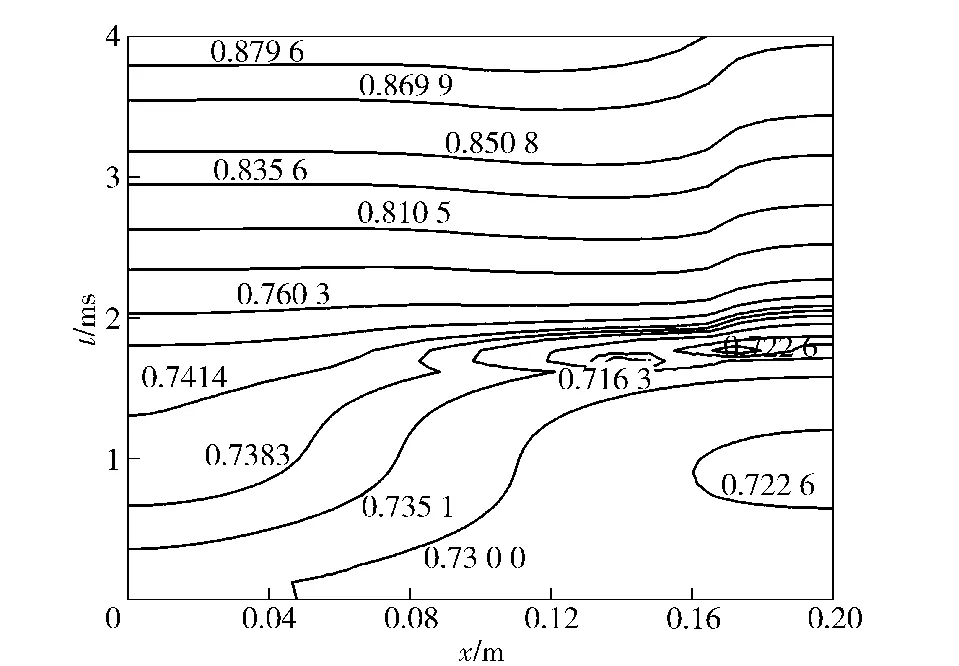
图5 不同时刻空隙率分布Fig.5 Calculated porosity distribution at x-t
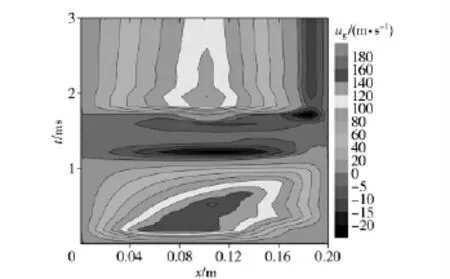
图6 不同时刻气相速度分布Fig.6 Calculated gas velocity distribution at x-t

图7 不同时刻固相速度分布Fig.7 Calculated solid velocity distribution at x-t

图8 不同时刻破孔流量分布图Fig.8 Calculated mass flow rate distribution of vent holes at x-t

图9 不同时刻颗粒表面温度及点火波阵面分布Fig.9 Calculated particle temperature and ignition wavefront distribution at x-t
4.2 不同因素对点火管性能的影响
大量的实验及数值模拟结果表明[1],不同的点火性能对压力波的发展、火焰波的传播以及整个内弹道性能有着显著的影响。点火管点火性能的主要因素包括传火孔位置、传火孔面积以及点火位置等,其中第1 排传火孔的位置是控制点火管内压力变化以及破孔规律的重要影响因素。为了进一步验证基于近似黎曼解模型所编制程序的适应能力,以及研究不同传火孔位置对点火管性能的影响,下面通过黎曼近似模型对其进行分析。
图10为点火管内不同破孔位置压力波对比图。从图中可以看出,随着第1 排传火孔位置的逐渐后移,点火管内压力逐渐提高,并且点火管内的最大压力波幅也会随着明显增大。这与理论分析及实验描述[1]均完全相一致。这种点火压力的提高,势必会造成膛内最大压力的上升,并且引起很大程度上的点火延时,给发射安全带来隐患。所以一般在选取第1 排传火孔位置时尽量靠近左端,但是相关研究表明[7],当点火管过于靠近左端时往往会造成炮口动能的降低,达不到火炮设计要求。因此需要考虑最大膛压和炮口速度的综合变化情况,对点火管第1 排破孔位置进行优化选择。

图10 不同破孔位置压力波动对比Fig.10 Comparison of pressure wave at different locations
5 结论
1)基于Roe 的近似黎曼解,通过具有TVD 性质的高阶重构以及两步分裂源项处理,获得了高阶精度的内弹道两相流近似黎曼解离散格式。
2)通过与激波管、源项验证等具有解析解的经典算例进行对比,验证了所构造高阶方法的准确性与稳定性。点火管算例的数值验证,准确形象地描述点火管内复杂两相流动的实际物理过程,实验验证了该方法处理火炮两相流问题的可靠性。
3)研究了合理设计传火孔位置可以改善点火管内瞬时性、均匀性及安全性等点火性能,并充分说明了所建立模型具有较强的适应能力。
4)以高精度近似黎曼解为基础,建立的火炮内弹道两相流模型,无需滤波、粘性修正以及将气体—固体两相分开处理,提高了对膛内强间断以及复杂波系的捕捉能力,改善了数值模拟的计算精度。
References)
[1] 金志明,袁亚雄,宋明.现代内弹道学[M].北京:北京理工大学出版社,1992.JIN Zhi-ming,YUAN Ya-xiong,Song Ming.Modern interior ballistic[M].Beijing:Beijing Institute of Technology Press,1992.(in Chinese)
[2] 袁亚雄,张小兵.高温高压多相流体动力学基础[M].哈尔滨:哈尔滨工业大学出版社,2005.YUAN Ya-xiong,ZHANG Xiao-bing.Multiphase hydrokinetic foundation of high temperature and high pressure[M].Harbin:Harbin Institute of Technology Press,2005.(in Chinese)
[3] Chang S C.The method of space-time conservation element and solution element:a new approach for solving the Navier-Stokes and Euler equations[J].Journal of Computational Physics,1995,119:259-324.
[4] 阎超.计算流体力学方法及应用[M].北京:北京航空航天大学出版社,2006.YAN Chao.Method and application of computational fluild dynamics[M].Beijing:Beijing University of Aeronautics and Astronautics Press,2006.(in Chinese)
[5] Toro E F.Riemann solvers and numerical methods for fluid dynamics[M].3rd.Berlin:Springer,2009.
[6] Lowe C,Clarke J.A class of exact solution for the Euler equations with sources[J].Mathematical and Computer Modeling.2002,(36):275-291.
[7] 张会生.高初速火炮新型点传火技术及装药优化研究[D].南京:南京理工大学,1998.ZHANG Hui-sheng.The optimization studies of new pattern ignition and flame spreading system and charge structure technology in high-velocity guns[D].Nanjing:Nanjing University of Science and Technology,1998.(in Chinese)

