抗高过载装药结构爆轰点火内弹道两相流仿真

张丁山，王浩，阮文俊，郭锦炎，冯国增

(1.西安近代化学研究所，陕西 西安710065;2.南京理工大学 能源与动力工程学院，江苏 南京210094)

0 引言

不同的武器发射装药系统均具有不同的点火过程，而不同的点火过程可通过点火方式和装药结构进行区分，即点火方式和装药结构只要二者之一在原基础上发生变化，就形成一新的点火过程，如二者均发生变化，则必须对由此产生的新点火过程进行研究，主要研究新点火过程的点传火特性和火药燃气压力变化规律［1-2］。本文研究了一种可应用于高过载环境下、火药装填的分层装药结构，其应用“化整为零”的思想，通过多层装药叠加实现以下主要目的:1)总装药量的需求;2)各层装药在高过载环境下保持良好的安定性;3)各层装药间具有良好的传火特性。为了提高各层装药的抗过载性，各层药盒均为钢制，药盒尺寸形状依据工程需求进行设计;为了避免火药颗粒的破碎，装填密度较高，装填后使火药颗粒不可自由运动。此装药结构经试验验证可以使高装填密度的小颗粒火药承受20 000～40 000g的过载，且过载持续时间为10～20 ms 的装药结构，该装药结构采用了爆轰点火，为了分析该装药结构下的点火过程中火药颗粒的运动和燃烧情况，以及此种装药结构下的传火特性即火药气体流动特性，在试验研究的基础上，利用内弹道两相流模型进行了数值仿真，得出点火过程中固相和气相运动参数的变化情况，对抗高过载装药结构下爆轰点火的点传火特性有了一定程度的了解和掌握，为将该结构采用爆轰点火投入到实际工程中提供理论依据。

1 物理模型

抗高过载装药结构下爆轰点火计算物理模型见图1.建模时模拟的时间段为从点火开始到药盒固定壳体炸开为止，模拟的对象为在爆轰点火方式下各层装药的运动与燃烧情况，通过计算研究此装药结构的点传火特性。

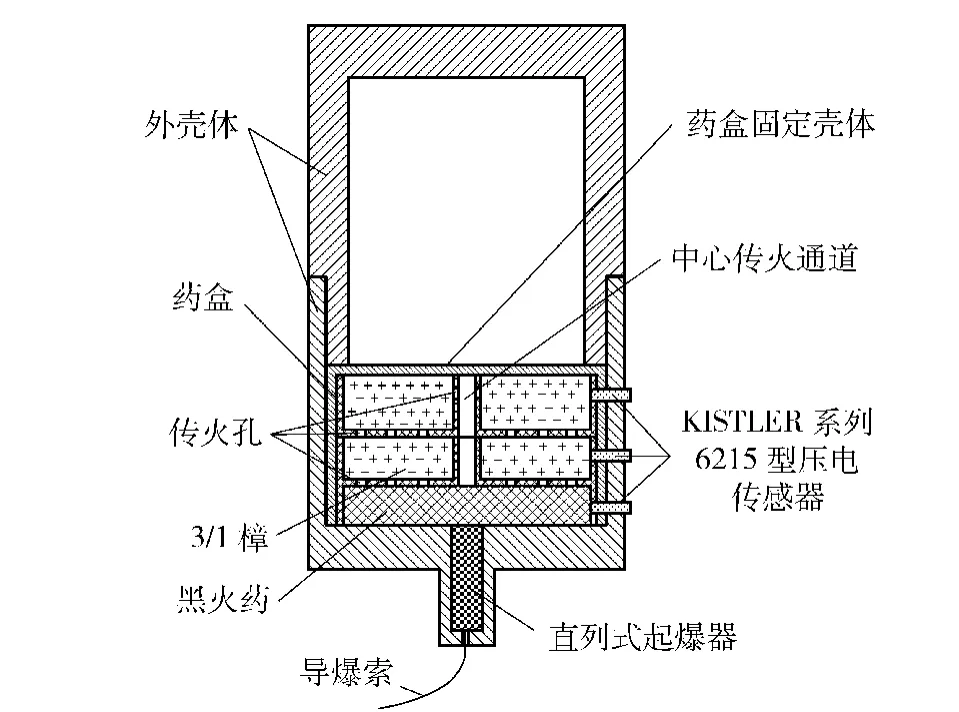
图1 抗高过载装药爆轰点火试验示意图Fig.1 The schematic drawing of charge structure which has overload protection with ignition by detonation

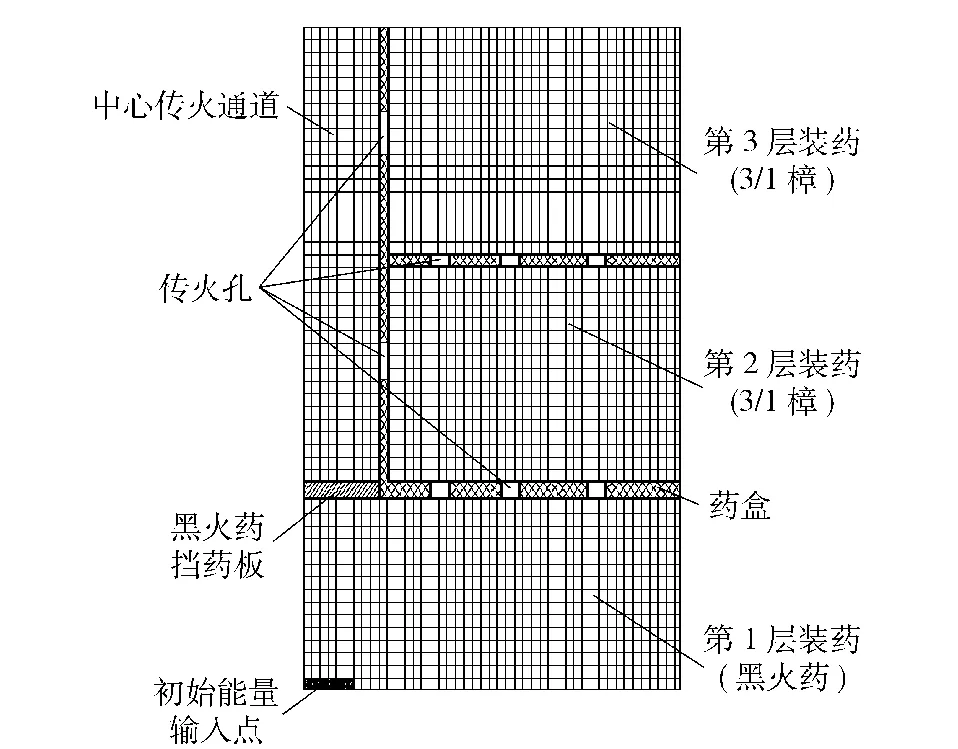
图2 计算网格划分示意图Fig.2 The schematic drawing of meshing

图2为编程计算时的物理模型及装药结构网格划分示意图。由于装药结构的轴对称性，故计算时只计算一半。另外，由于药盒不参与火药燃烧反应，划分网格时未对其进行划分［3］。

计算此点传火过程分为3 个阶段:第1 阶段为直列式起爆器起爆，爆轰产物及爆轰波作用于黑火药，当达到黑火药着火点时，黑火药开始燃烧;第2阶段为黑火药燃烧产生的气体通过药盒底部的传火孔和药盒中间的传火通道进入第1 层3/1 樟装药，当达到3/1 樟火药的着火点时，第1 层3/1 樟火药开始燃烧;第3 阶段为黑火药燃气通过中间传火通道进入第2 层3/1 樟装药，同时第1 层3/1 樟火药的燃烧气体通过药盒底部的传火孔也进入第2 层3/1 樟装药，当达到3/1 樟火药的着火点时，第2 层3/1 樟火药开始燃烧，当第2 层3/1 樟装药顶端的压力达到药盒固定壳体的承压极限时，药盒固定壳体炸开，计算结束。在建立各阶段计算模型时，作出如下假设:

1)直列式起爆器对黑火药的能量输出认为是瞬间完成的。

2)直列式起爆器起爆瞬间，由于爆轰产物的传递具有很好的方向性，故认为爆轰产物对黑火药的作用区域仅为正对直列式起爆器的那部分区域即作用区域仅为直列式起爆器直径大小。

3)直列式起爆器起爆后输出物质既有气体产物，又有颗粒产物，建立气相、固相质量和动量守恒方程时，气体产物归第1 层装药内的气相考虑，颗粒产物近似为黑火药颗粒并一起归为第1 层装药内的固相考虑。

4)计算时不考虑冲击波对第1 层药盒结构的影响，当各层药盒底面两侧火药气体的压力差达到40 MPa 时，药盒底面发生破坏，底面传火孔随之消失。

5)当药盒底面破坏后，不考虑药盒底面碎片对火药气体流动和火药颗粒运动产生的影响。

6)依据试验后回收的药盒，可以看出，药盒底面破坏，但中心传火通道仍较为完好，故建模计算时，假设中心传火通道在整个点火过程中结构尺寸不变。

7)对于从一层装药流动到另一层装药内的火药颗粒，计算时，将这部分火药颗粒的种类近似为其当前所在药层的火药种类。

8)其余关于火药颗粒燃烧的假设和火药燃烧气体的假设见文献［4］.

2 数学模型

2.1 第1 阶段方程组的建立

2.1.1 气相质量守恒方程

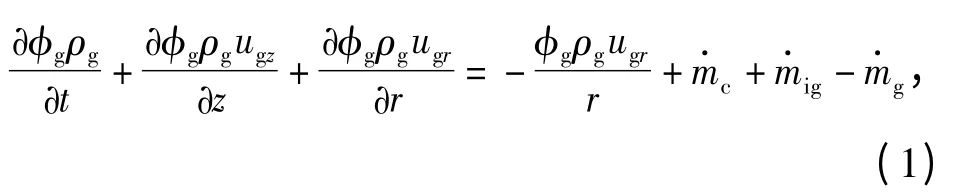
式中:ρg为气相密度(kg/m3);φg为气相空隙率;为火药气体的生成速率(kg/(m2·s))；为点火源的气体生成速率(kg/(m2·s));ugz为气相轴向速度(m/s);ugr为气相径向速度(m/s);为黑火药燃烧气体流出速率(kg/(m2·s)).

2.1.2 固相质量守恒方程

式中:ρs为固相密度(kg/m3);φs为固相空隙率，φs=1-φg;usz为固相轴向速度(m/s);usr为固相径向速度(m/s);为黑火药固相流出速率(kg/(m2·s)).

2.1.3 气相动量守恒方程

轴向

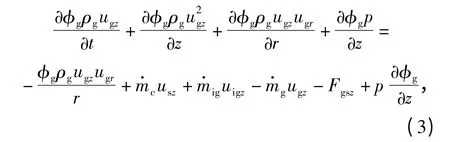
式中:Fgsz为气固两相间轴向阻力(N);uigz为点火源生成气体的轴向流动速度(m/s);p 为压力(Pa).

径向

式中:Fgsr为气固两相间径向阻力(N);uigr为点火源生成气体的径向流动速度(m/s).

2.1.4 固相动量守恒方程

轴向

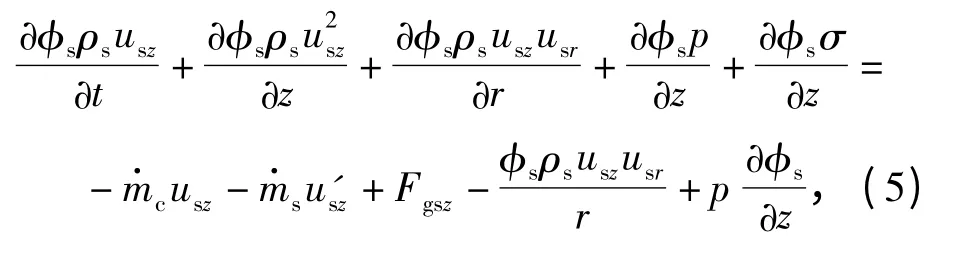
式中:σ 为颗粒间应力(MPa);u'sz为固相流出轴向速度(m/s).

径向

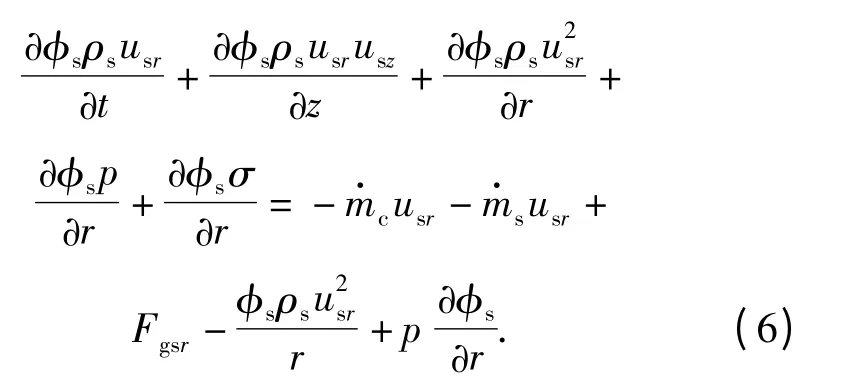
2.1.5 气相能量守恒方程

式中:Eg为气相比内能;ep为火药化学潜能(J/kg);Hig为点火药总焓(J/kg)；为单位体积内固相颗粒的表面积，即固相比表面积(m2);q 为考虑对流和辐射两种形式热交换时相间热交换比热流(J/m2).式中各变量计算公式见文献［4］.

写成守恒型矢量形式，即

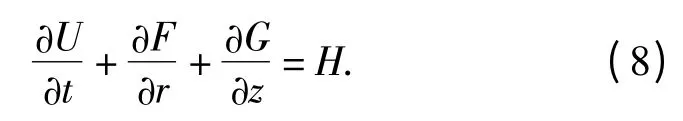
2.1.6 辅助方程

主要包括:1)火药燃烧方程;2)黑火药燃烧方程

以上所列辅助方程均见文献［4］.

2.1.7 初始条件

初始条件包括:ugr=ugz=0;usr=usz=0;p=p0=1.01 × 105Pa;Tg=Ts=T0=288 K;ρg=［RT0/(p0+β)］-1;φg=φg(z)=0.625.

2.1.8 边界条件

边界条件包括:1)所有壁面都满足速度分量沿外法线方向的分量为0;2)中心轴线边界条件满足轴对称关系式，见文献［4］.其余固定边界，采用镜面反射法。

2.2 第2、3 阶段方程组的建立

第2、3 阶段的方程组与第1 阶段的方程组基本相同，只是在火药气体的流入流出以及火药颗粒的流入流出上做相应的修改。

2.3 中心传火通道方程组的建立

中心传火通道的方程组与第2、3 阶段的方程组基本相同，只是在初始条件中气相初始空隙率为1，其余条件与第1 阶段的相同。

3 数值计算方法

3.1 差分格式

采用MacCormack 预估校正二步显格式［4］。

3.2 稳定性条件

采用的稳定性条件为适用于轴对称二维两相流的稳定性条件［4］。

3.3 人工黏性

应用Rusanov 方法［4］加入人工黏性项。

4 数值模拟结果和分析

表1列出了编程计算过程中网格的划分情况以及爆轰点火器参数，表2列出了各层的装药情况，关于计算中所需的火药参数可查阅文献［5］。

表1 网格及点火器主要参数Tab.1 The main parameters of mesh and igniter

表2 各层药盒及装药参数Tab.2 The main parameters of powder box and charging

4.1 第1 层装药部分计算结果

图3为点火后0.42 ms 即计算结束时第1 层装药内压力分布图;图4为第2 层药盒底面破坏前，第1层装药顶端火药颗粒间应力的变化曲线;图5为第1 层装药右壁处火药颗粒间应力的变化曲线。从图3可以看出，计算结束时，第1 层装药内的压力分布情况，其中正对中心传火通道的区域(r 为0～8 mm)，由于火药气体的大量流出，压力下降最为明显。从图4、图5可以看出，在点火冲击波的作用下，第1 层装药顶端和右壁处火药颗粒间的应力将达到100 MPa 左右，此时靠近第1 层装药顶端的火药颗粒一般不会由于应力过高而发生破碎。

图6为点火后0.38 ms 时固相空隙率分布图。从中可以得出此时第1 层装药内的火药颗粒已剩余很少，进而可判断出在计算结束及0.42 ms 时，第1 层装药几乎全部烧完。

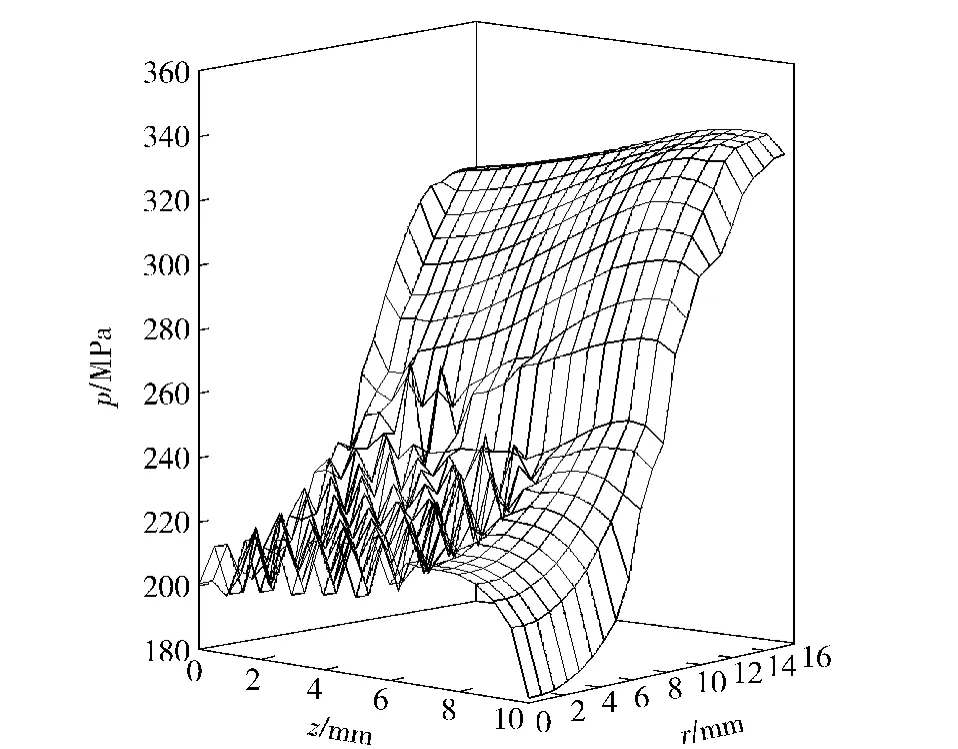
图3 点火后0.42 ms 时压力分布图Fig.3 Pressure distribution pattern at 0.42 ms after ignition

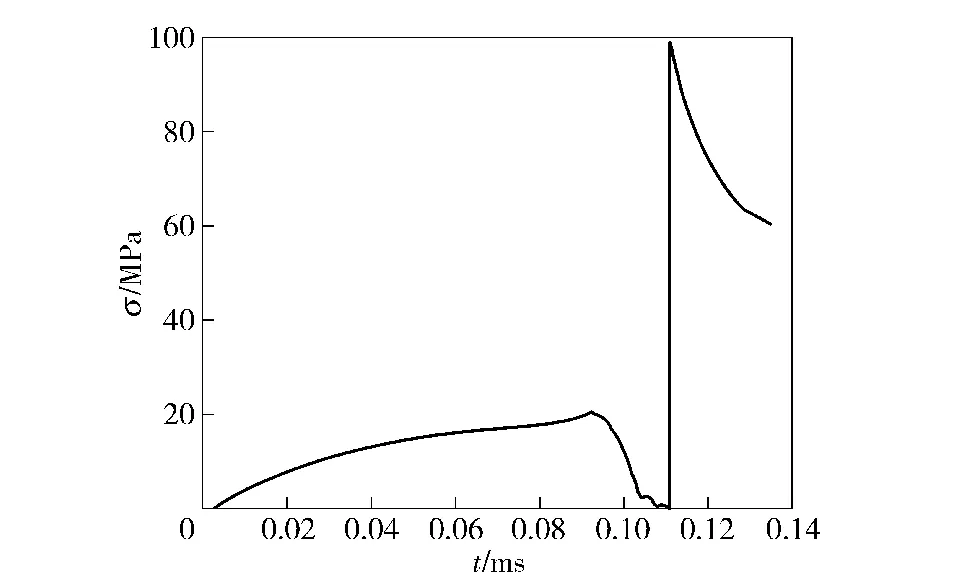
图4 第1 层装药顶端火药颗粒间应力Fig.4 Stress of powder grain at top of the first charging layer

图5 第1 层装药右壁火药颗粒间应力Fig.5 Stress of powder grain at the right of the first charging layer

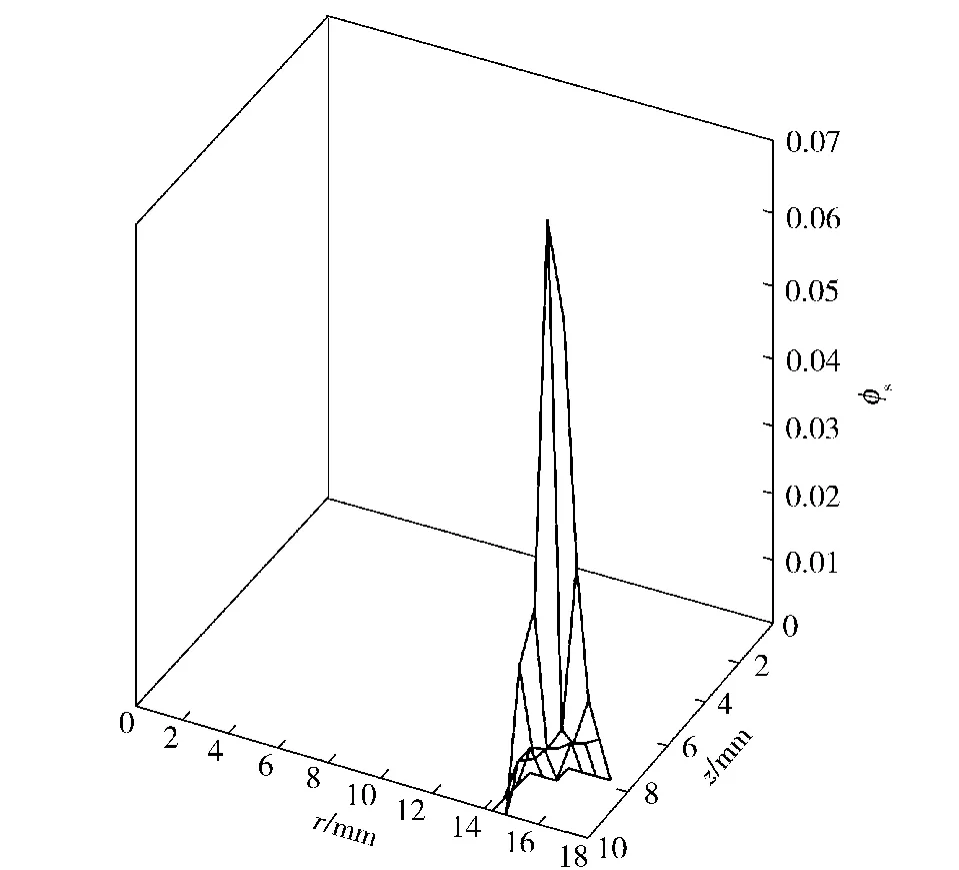
图6 点火后0.38 ms 时固相空隙率分布图Fig.6 Solid phase void ratio distribution pattern at 0.38 ms after ignition

4.2 第2 层装药部分计算结果

图7为计算结束时第2 层装药内压力分布图;图8为第3 层药盒底面破坏前，第2 层装药顶端火药颗粒间的应力变化曲线;图9为第2 层装药右壁处火药颗粒间应力的变化曲线。从中可以得出，第2 层装药内的火药颗粒在整个点火过程中不会由于应力过高而发生破碎现象。

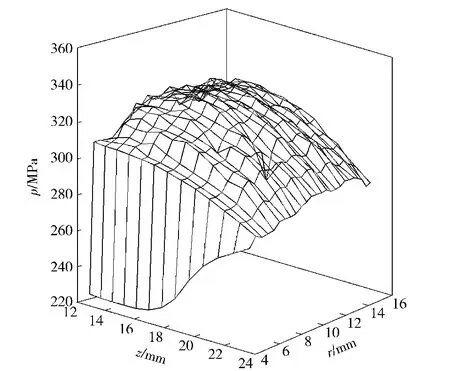
图7 点火后0.42 ms 时压力分布图Fig.7 Pressure distribution pattern at 0.42 ms after ignition

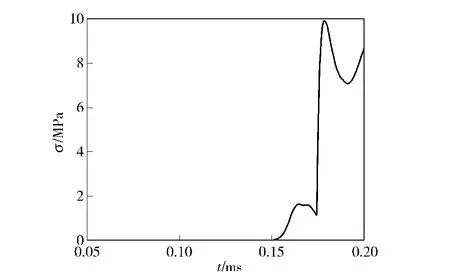
图8 第2 层装药顶端火药颗粒间应力Fig.8 Stress of powder grain at top of the second charging layer

图10为压力测试点处固相空隙率变化曲线。从中可以看出，随着第2 层药盒底面和第3 层药盒底面的破坏，火药颗粒在火药气体的带动下运动频繁，同时在计算结束时，第2 层装药内的火药尚未完全烧完。

4.3 第3 层装药部分计算结果

图11为计算结束时第3 层装药内压力分布图;图12为第3 层装药顶端火药颗粒间应力的变化曲线;图13为第3 层装药右壁处火药颗粒间应力的变化曲线。从中可以看出:随着火药颗粒的堆积，第3 层装药顶端火药颗粒间的应力达到96 MPa 左右，而第3 层装药右壁处火药颗粒间的应力将达到70 MPa左右，此两处的火药颗粒一般不会发生破碎。

图14为测试点处固相空隙率的变化曲线。从中可以看出，在火药气体的带动下，火药颗粒向第3 层装药顶端堆积，且第3 层装药内火药颗粒的堆积程度是3 层装药中最为严重的。

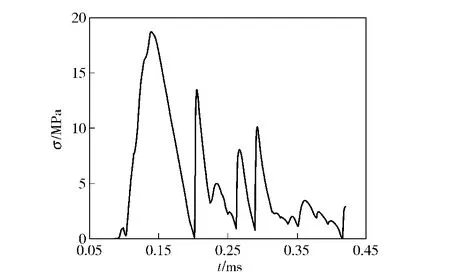
图9 第2 层装药右壁火药颗粒间应力Fig.9 Stress of powder grain at the right of the second charging layer

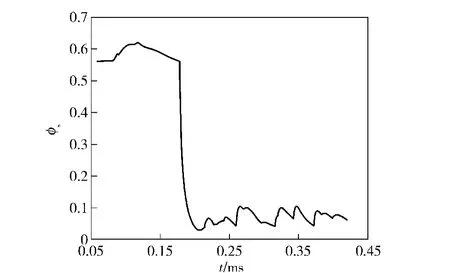
图10 测试点处固相空隙率变化曲线Fig.10 The changing curve of solid phase void ratio at test point

图11 点火后0.42 ms 时压力分布图Fig.11 Pressure distribution pattern at 0.42 ms after ignition

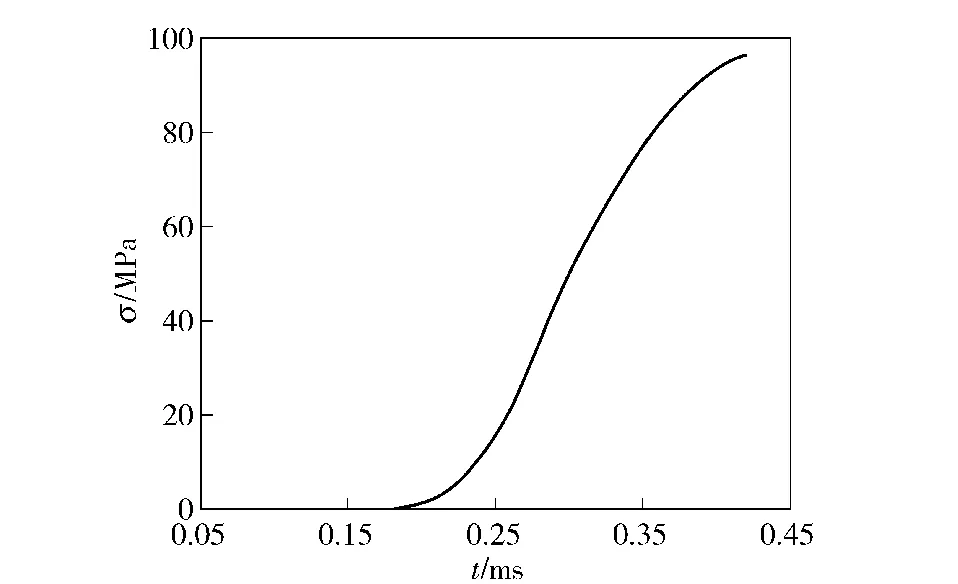
图12 第3 层装药顶端火药颗粒间应力Fig.12 Stress of powder grain at the top of the third charging layer

图13 第3 层装药右壁火药颗粒间应力Fig.13 Stress of powder grain at the right of the third charging layer

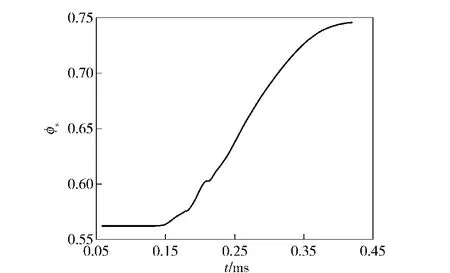
图14 测试点处固相空隙率变化曲线Fig.14 The changing curve of solid phase void ratio at test point

4.4 测试点处压力试验值与计算值对比

第1、2 层装药测试点处压力计算结果与试验结果符合较好(见图15、图16)，第3 层装药测试点处压力计算结果与试验结果相比存在一定程度的偏差(见图17)，其中偏差主要为冲击波的传播计算、第3层装药内火药气体压力上升的速度以及药盒固定壳体炸开的时间，以上偏差主要由以下原因造成的:1)计算冲击波传播的经验公式以及计算冲击波衰减的经验公式与实际存在偏差;2)建立模型时，未考虑冲击波对药盒结构的影响，以及未考虑冲击波在第1 层装药内的反射和冲击波在第2、3 层装药内的传播。虽然压力计算结果与试验所得存在偏差，但对整个点传火过程进行的两相流计算以及得到的计算结果，为了解和掌握抗高过载装药结构的点传火特性提供了参考。

图15 第1 层测试点压力曲线Fig.15 The pressure curves of first layer at test point

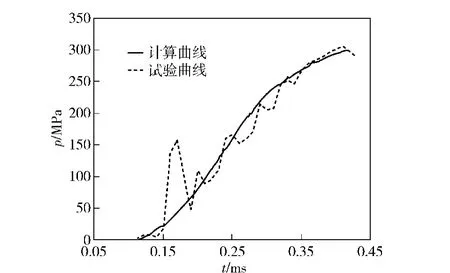
图16 第2 层测试点压力曲线Fig.16 The pressure curves of second layer at test point

5 结论

通过对计算结果的分析，得出抗高过载装药结构以及采用爆轰点火时具有以下点传火特性:1)采用爆轰直接点火的方式，可以实现微秒级点火，爆轰点燃火药的传热方式以对流传热和辐射传热为主，同时进行热传导;2)爆轰点火时的冲击波在药室内的传播和反射显著，故爆轰点火方式可以应用于对点火初期压力波动要求较低且需快速点火的场合;3)计算结束时，第1 层装药几乎全部烧完，第2 层装药内的火药颗粒有一部分流动到第3 层装药内，使得第3 层装药内顶端附近区域内火药颗粒的堆积程度最为严重;4)第1 层装药内靠近壁面处的火药颗粒和第3 层装药内靠近顶端及右壁处的火药颗粒在点传火过程中一般不会由于应力过高而发生破碎。

图17 第3 层测试点压力曲线Fig.17 The pressure curves of third layer at test point

抗高过载装药结构下爆轰点火的两相流计算研究中，除上述造成计算结果与试验结果存在较小程度偏差的原因外，另外由于计算过程中网格划分数量相对较少，使得应用计算结果画出的各种分布图较为粗糙，对上述因素的完善将在后续工作中完成。

References)

［1］ 王浩.粘结式随行装药两相流内弹道模型及其计算［J］.弹道学报，1998，10(4):31-36.WANG Hao.Interballistic simulation and computation of twophase flow of travelling charge［J］.Journal of Ballistic，1998，10(4):31-36.(in Chinese)

［2］ 张小兵，金志明，袁亚雄.分装式高装填密度火炮内弹道二维多相流数值模拟［J］.兵工学报，1998，19(1):10-15.ZHANG Xiao-bing，JIN Zhi-ming，YUAN Ya-xiong.Two-dimensional multi-phase flow numerical simulation of interior ballistics processes in a separated-loaded gun［J］.Aacta Aamamentarii，1998，19(1):10-15.(in Chinese)

［3］ 张小兵，翁春生，袁亚雄，等.轴对称二维颗粒轨道模型［J］.弹道学报，1997，9(1):60-64.ZHANG Xiao-bing，WENG Chun-sheng，YUAN Ya-xiong，et al.An axisym metrical particle trajectory model and its smulation［J］.Journal of Ballistic，1997，9(1):60-64.(in Chinese)

［4］ 翁春生，王浩.计算内弹道学［M］.北京:国防工业出版社，2006.WENG Chun-sheng，WANG Hao.Computational interior ballistics［M］.Beijing:National Defense Industry Press，2006.(in Chinese)

［5］ 金志明，翁春生.火炮装药设计安全学［M］.北京:国防工业出版社，2001.JIN Zhi-ming，WENG Chun-sheng.The safety theory of gun charging［M］.Beijing:National Defense Industry Press，2001.(in Chinese)