光电跟踪系统的激光回波率下界估计
索晓峰,楚天鹏,盛安冬,戚国庆
(南京理工大学 自动化学院,江苏 南京210094)
在光电跟踪系统中,目标坐标测定仪是一类配有图像处理功能的连续目标航路参数测量设备[1]。激光回波率则是指测定仪接收到的有效回波数与发射的重频激光脉冲数的比率[2],其直接关系到航路是否能有效建立以及目标运动参数的估计性能,因而是重要的设计指标之一。
不完全量测是指探测概率小于1 的量测[3],其下的跟踪估计问题,是近几年比较热门的研究课题。在不完全量测下,跟踪系统的数据探测往往利用服从Bernoulli 分布的随机变量进行描述。
在实际工程中,当其他条件相同时,光电跟踪系统的估计性能往往随着激光回波率的下降而降低。因此,本文给出了一个激光回波率的下界,当跟踪系统实际回波率高于这个下界值时,滤波器统计意义下的估计误差协方差对任意的估计初值均收敛,即可以建立有效的航路;若实际激光回波率低于这个下界,则统计意义下的估计误差协方差可能会发散,导致无法建立有效的航路。
1 问题描述
传统光电跟踪系统球坐标下的位置量测变换到笛卡尔坐标系下,跟踪系统可表示为:
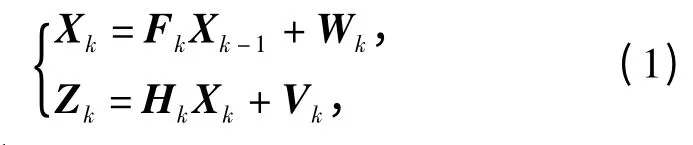
式中:Xk∈Rn×1为k 时刻的目标状态;Fk为适维状态转移矩阵;Wk∈Rn×1为0 均值协方差为Qk的高斯白噪声;Zk=[xkykzk]T为笛卡尔坐标系下的位置转换量测;Hk=[I3×303×(n-3)]为笛卡尔坐标系下量测矩阵;为笛卡尔坐标系下位置转换量测误差,并且服从均值为零协方差为Rk的高斯分布。同时,目标初始状态误差、目标运动噪声Wk以及跟踪系统转换量测噪声Vk之间互不相关。
当目标测定仪的激光光束打到目标上,并且能被接收,则称测定仪接受到了有效的激光回波;反之,若激光没有回波或者回波未被接收,则称测定仪回波无效。对于本文所讨论的坐标测定仪,为简化问题讨论并不失一般性,将有效回波目标区域定义为一宽为2a、高为2b 的矩形域,如图1所示。
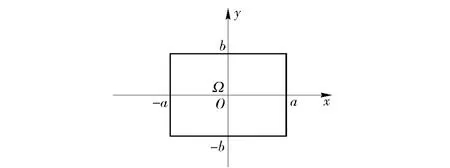
图1 靶标坐标系Fig.1 Target coordinates
用一个服从Bernouli 分布的随机变量dk来描述测定仪激光回波是否有效。令 dk=即激光跟踪系统的激光打在有效区域Ω,并且接受到有效的回波;dk=0,即激光跟踪系统的激光打在有效区域Ω 外,或者激光跟踪系统没有接受到回波。dk的概率分布为p{dk=1}=λ,p{dk=0}=1-λ,λ 即为光电跟踪系统的激光回波率。
则在不完全量测下,(1)式可用下式替代
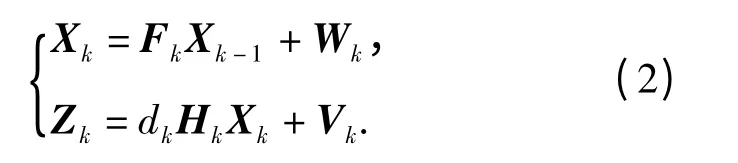
dk与量测噪声Vk满足,
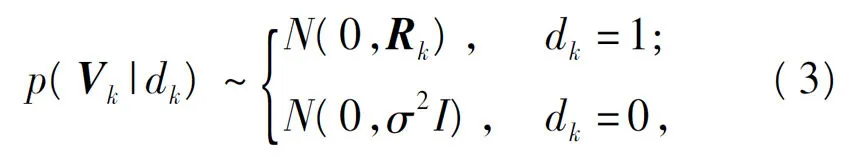
式中:N(a,b)为变量服从均值为a,方差为b 的高斯分布。dk=1,回波有效,噪声变量服从均值为0,方差为Rk的正态分布;dk=0,回波无效,对应的σ 取极限形式:σ2→∞,噪声变量的方差为∞.
2 激光回波率下界与估计性能
2.1 有效滤波的激光回波率下界
对于(2)式所表示的光电跟踪系统模型,依据不完全量测的理论,采用标准Kalman 滤波器对目标状态进行估计,则可得滤波器时刻k+1 状态估计的一步预测误差协方差Pk+1满足
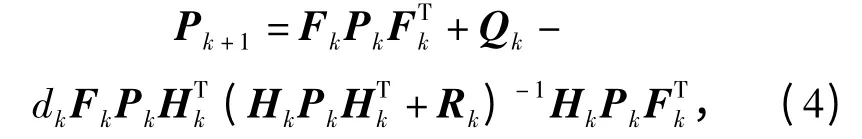
则统计意义下的光电跟踪系统修正代数Riccati 方程(MARE)为
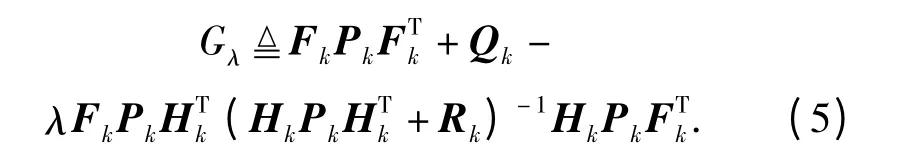
依据文献[4],可得
引理1 若(Fk,Q1/2k)可控,(Fk,Hk)可观,Fk不稳定,且∃Rmax,s.t.Rmax≥E(Rk),∀k,则∃λc∈[0,1),s.t.
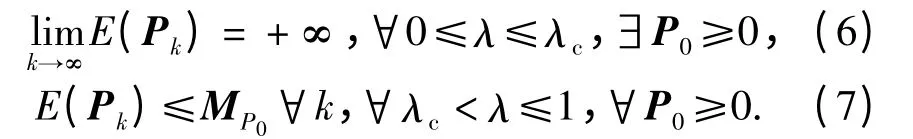
其中MP0≥0,由引理1 可知当跟踪系统可控可观,并且跟踪系统统计意义下的量测噪声协方差存在某个上界时,跟踪系统存在一个临界回波率λc.当跟踪系统的回波率小于或者等于临界回波率λc时,跟踪系统统计意义下的估计误差协方差对某些估计初值将会发散;而当跟踪系统的回波率大于临界回波率λc时,跟踪系统统计意义下的估计误差协方差对任意估计初值均会收敛。接下来将进一步给出跟踪系统临界回波率λc的预估上下界。
引理2 若∃Rmax,s.t.Rmax≥E(Rk),∀k,则
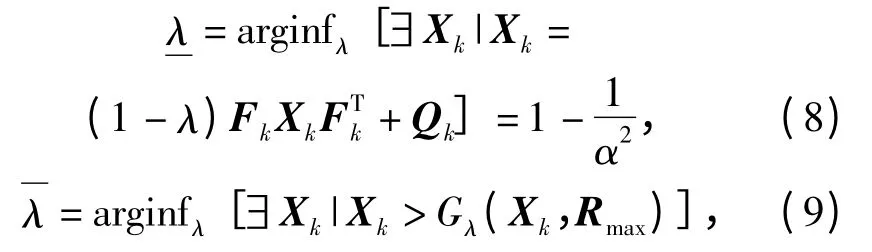
式中:α=max|σi|,σi为矩阵Fk的特征值。(8)式和(9)式给出了临界回波率的取值范围。考虑到Fk的特征值往往相等并且等于1,此时有α=1,λ=0.那么临界回波率λc满足0≤λc≤
当对于任意的初值P0,E[Pk]均有界时,才能获得有效的滤波航路。依据引理1 和引理2,可得
推论 若∃Rmax,s.t.Rmax≥E(Rk),∀k,令
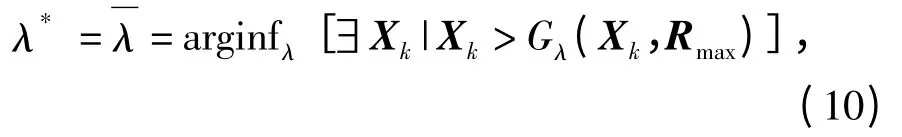
当λ≥λ*时,对于∀P0≥0,∃MP0≥0,严格满足E[Gλ]≤MP0.
λ*即为严格意义下,能获得有效滤波航路的激光回波率下界。
定义一个辅助函数
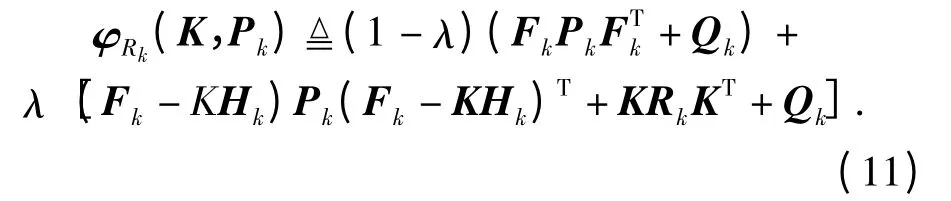
当K=FkPk(Hk)T[HPk(Hk)T+Rk]≜K*,有Gλ(Pk,Rk)=φRk(K*,Pk)≤φRk(K,Pk),当∃X,s.t.X > Gλ(X,Rmax)时,有∃(KX,X),s.t.X >Gλ(X,Rmax)=φRmax(KX,X ),其 中 KX=FkX(Hk)T[HkX (Hk)T+ Rmax];又当∃(K,X),s.t.X >φRmax(K,X)时,有∃X,s.t.X >φRmax(K,X)≥gλ(X,Rmax).即(10)式等价为

由(12)式看出,λ*被描述为一个非线性矩阵不等式(NMI)的最优解。通常采用求解双线性矩阵不等式(BMI)问题的摄动线性化方法来设计求解上述非线性矩阵不等式(NMI)的最小化问题[5]。基本思想是:先将NMIX >φRmax(K,X)关于变量λ,K,X 摄动线性化,再在摄动范围内求解λ,K,X 的摄动量,使探测概率λ 减小,直至X >φRmax(K,X)关于变量K,X 没有可行解,或者λ 的摄动量甚微结束。
2.2 不完全量测下的估计性能研究
一般来说,CRLB 被广泛应用为跟踪系统的估计性能指标,它给出了滤波器估计误差协方差的理论下界。跟踪系统的估计误差协方差满足Pk|k≥Jk-1,其中Jk为Fisher 信息矩阵(FM),CRLB 是FM的逆,Ck=J-1k.由文献[3]可知,不完全量测下的Jk修正递推公式为
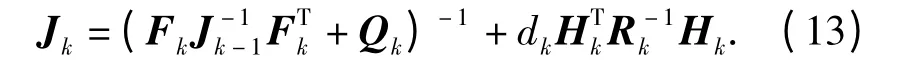
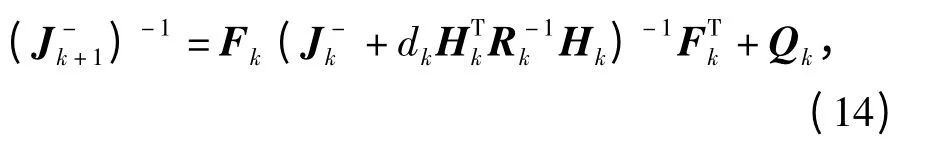
则修正的CRLB 下界为
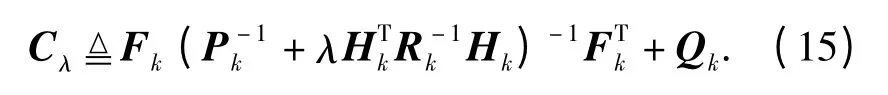
(15)式即为统计意义下,目标测定仪激光回波率与修正的CRLB 的关系。
3 分析与应用
下面针对实际靶场测量到的3 条标准航路,对光电跟踪系统激光回波率下界和性能指标进行仿真分析。
光电跟踪系统数据量测精度为σr=5 m,σθ=0.1°,σφ=0.3°;回波周期T=0.32 s;对于航路一,取目标状态对于航路二和航路三取目标状态
3.1 航路一
航路一为实际靶场测量到的一条匀速直线航路,航速近似为250 m/s,航高近似1 000 m,航捷近似750 m.X0=[-172,-41,-4 753,250,1 091,5]T.
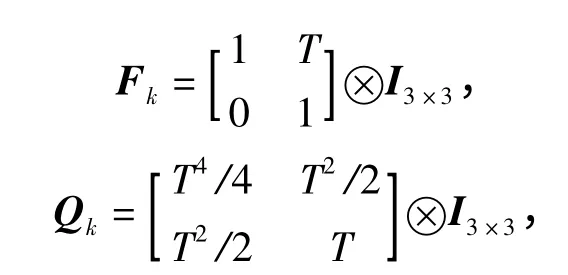
式中:T 为跟踪系统采样周期;⊗为Kronecher 乘积;I3×3为三阶单位矩阵。首先给出E(Rk)与采样时间的关系曲线如图2所示。
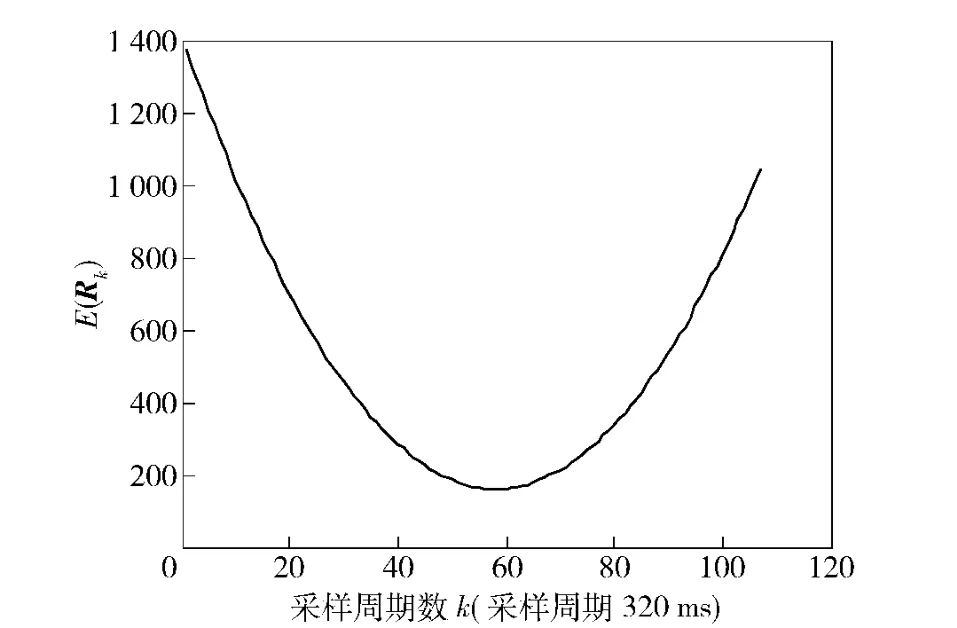
图2 E(Rk)与采样周数数k 的关系(航路一)Fig.2 Relationship between E(Rk)and k in airway 1
由图2可以看出,Rmax=E(R1)≥E(Rk),∀k.此时最大迭代次数为100,根据摄动迭代算法求激光回波率的下界。当取不同振动幅度的迭代计算结果如表1所示,τi>0,i=1,2,3 表示摄动幅度。从表中可以看出,激光回波率下界为48.7%.
采用不同的激光回波率,通过滤波所得到的航路,可以看出激光回波率对目标航路测定的影响,如图3所示。
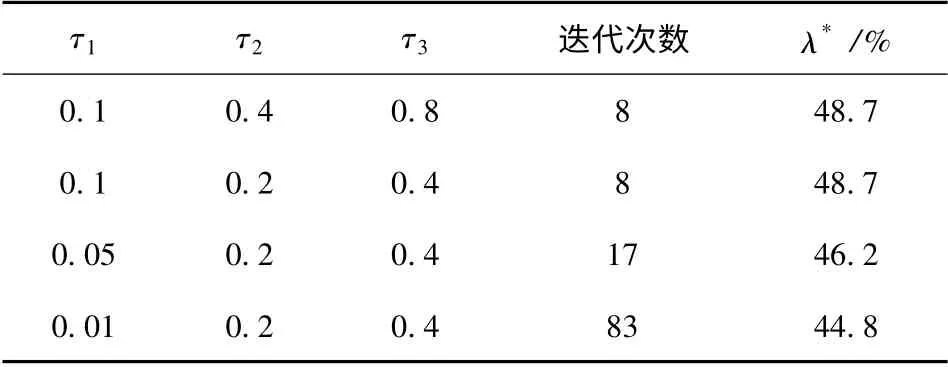
表1 航路一不同摄动幅度的迭代计算结果Tab.1 Iterative results of different perturbation intensity in airway 1
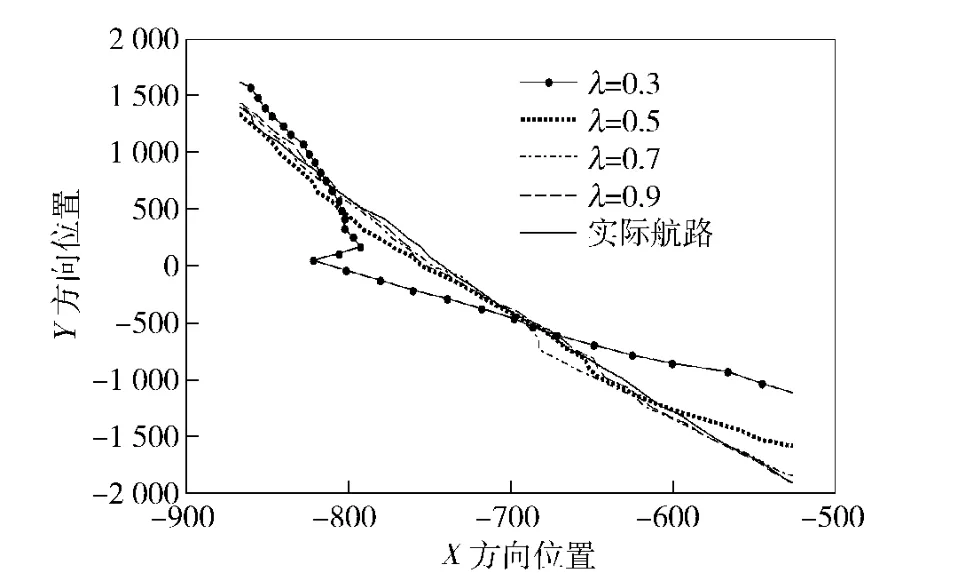
图3 激光回波率对目标航路测定的影响(航路一)Fig.3 Effect of laser echo rate on target measurement in airway 1
针对航路一,采取不同的回波率,可得在不同情况下跟踪性能指标CRLB 下界与λ 的关系,如图4所示。
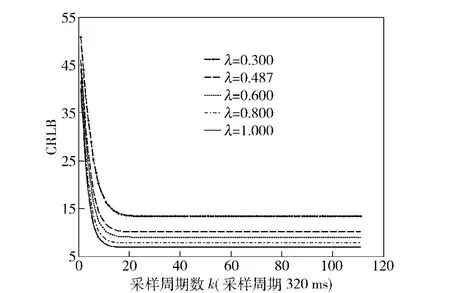
图4 回波率与CRLB 关系(航路一)Fig.4 Relationship between laser echo rate and CRLB in airway 1
3.2 航路二
航路二为匀速圆周航路,航高近似1 000 m,运动半径r=5 000 m,运动角速度ω=0.05 rad/s.X0=[4 000,-200,-10,3 000,150,-7.5,1 000,0,0]T.
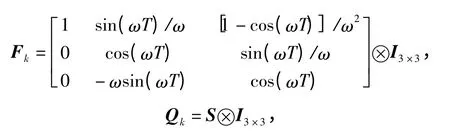
其中:
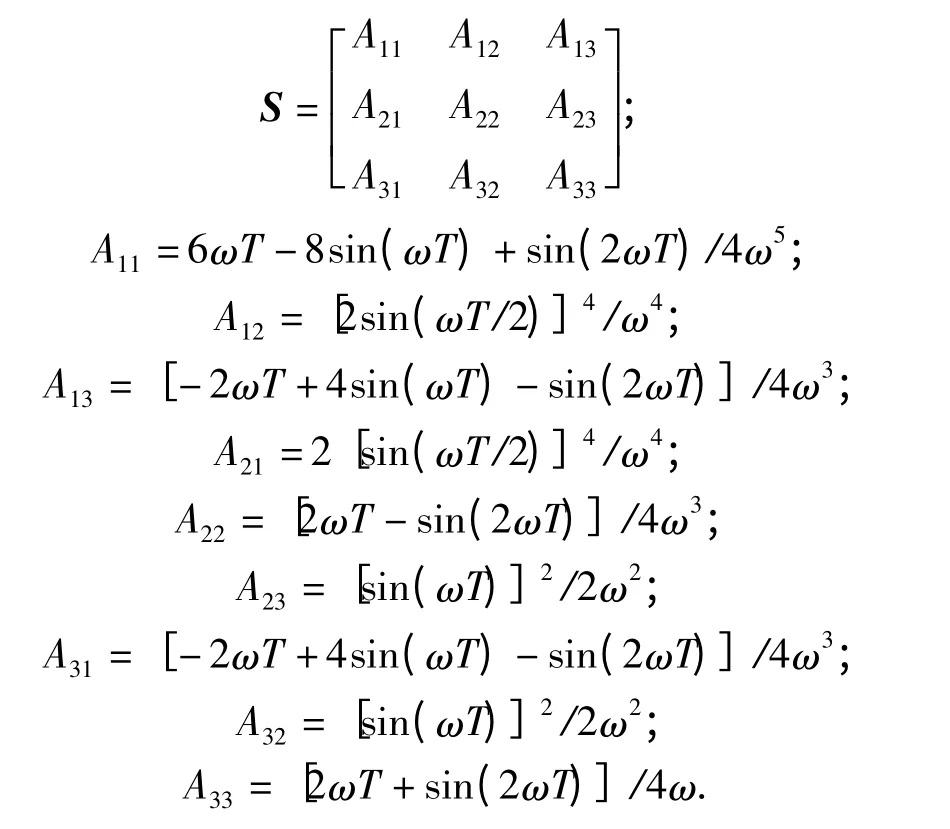
式中:T 为跟踪系统采样周期;⊗为Kronecher 乘积;I3×3为三阶单位矩阵。首先给出E(Rk)与采样时间的关系曲线,如图5所示。
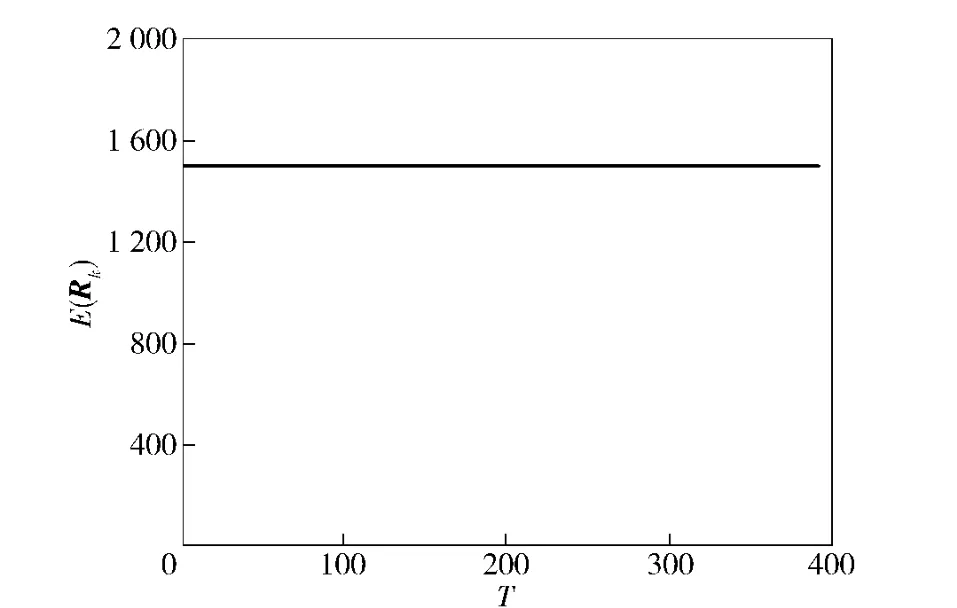
图5 E(Rk)与采样周数数k 的关系(航路二)Fig.5 Relationship between E(Rk)and k in airway 2
由图5可以看出,Rmax=E(R1)≥E(Rk),∀k.此时最大迭代次数为100,根据摄动迭代算法求激光回波率的下界。当取不同振动幅度的迭代计算结果如表2所示,τi>0,i=1,2,3 表示摄动幅度。从表中可以看出,激光回波率下界为43.2%.
采用不同的激光回波率,通过滤波所得到的航路,可以看出激光回波率对目标航路测定的影响,如图6所示。

表2 航路二不同摄动幅度的迭代计算结果Tab.2 Iterative result of different perturbation intensity in airway 2
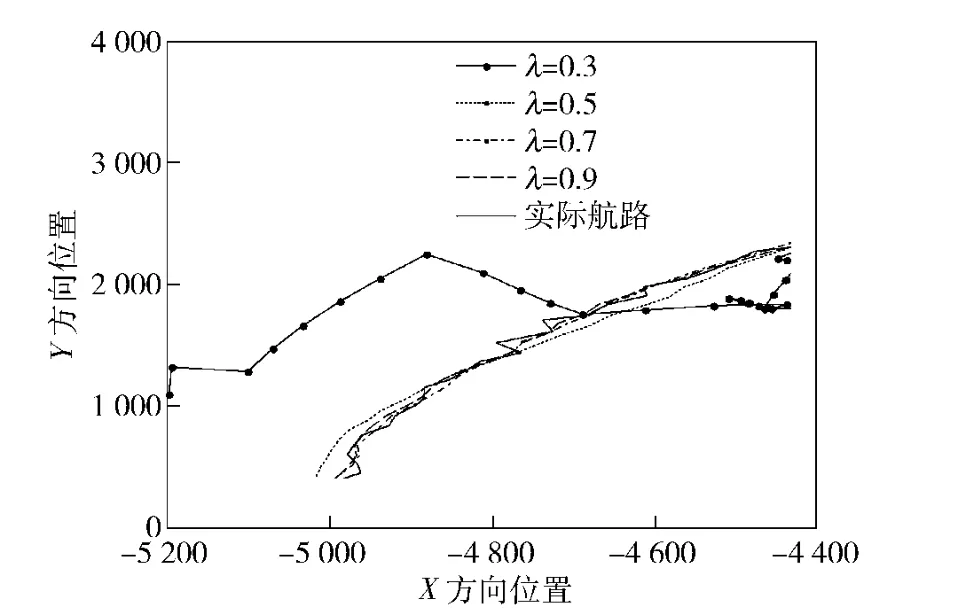
图6 激光回波率对目标航路测定的影响(航路二)Fig.6 Effect of laser echo rate on target measurement in airway 2
针对航路二,采取不同的回波率,可得在不同情况下跟踪性能指标CRLB 下界与λ 的关系,如图7所示。
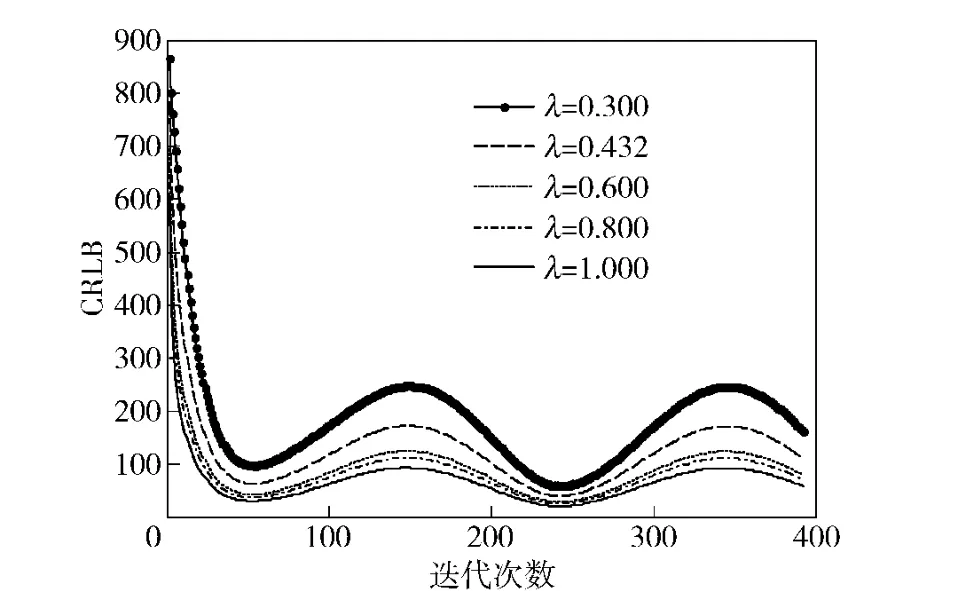
图7 回波率与CRLB 关系(航路二)Fig.7 Relationship between laser echo rate and CRLB in airway 2
3.3 航路三
航路三为一条俯冲航路,航高近似4 000~2 000 m,纵向加速度10 m/s2,水平速度120 m/s,航捷500 m,X0=[-1 939.2,120,0,500,0,0,4 000,0,-10]T.
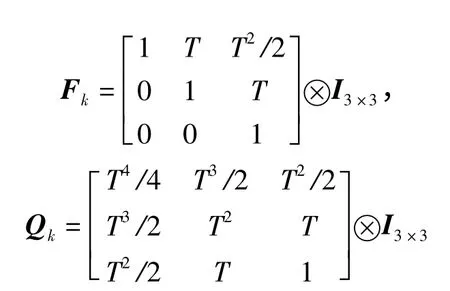
式中:T 为跟踪系统采样周期;⊗为Kronecher 乘积;I3×3为三阶单位矩阵。首先给出E(Rk)与采样时间的关系曲线如图8所示。
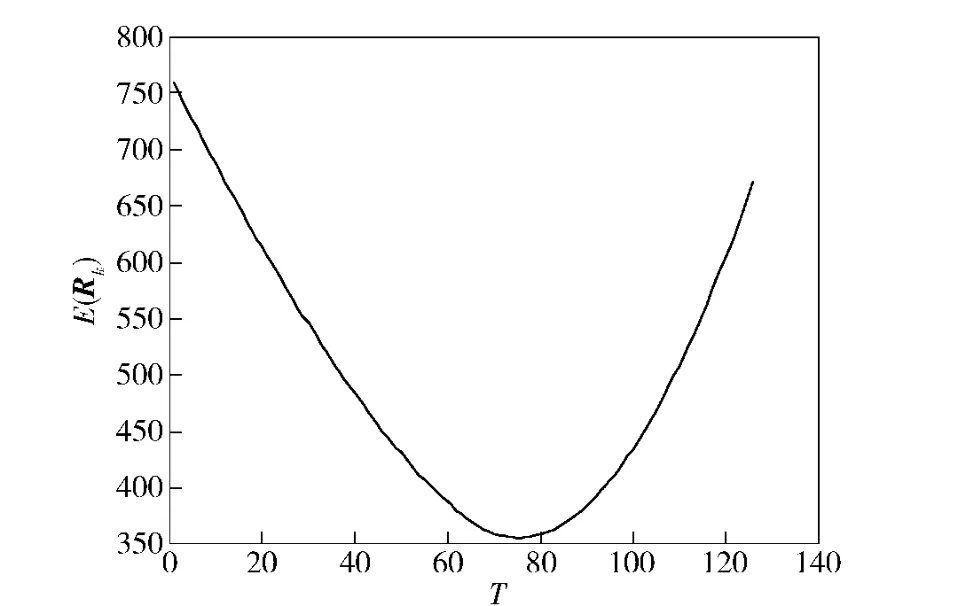
图8 E(Rk)与采样周数数k 的关系(航路三)Fig.8 Relationship between E(Rk)and k in airway 3
由图8可以看出,Rmax=E(R1)≥E(Rk),∀k.此时最大迭代次数为100,根据摄动迭代算法求激光回波率的下界。当取不同振动幅度的迭代计算结果如表3所示,τi>0,i=1,2,3 表示摄动幅度。从表中可以看出,激光回波率下界为47.6%.
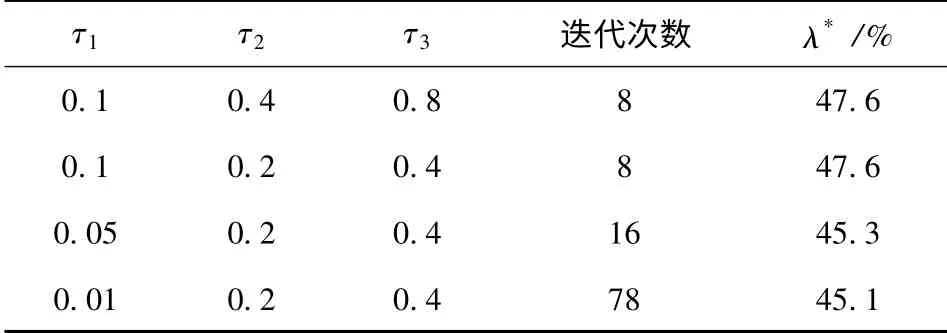
表3 航路三不同摄动幅度的迭代计算结果Tab.3 Iterative result of different perturbation intensity in airway 3
采用不同的激光回波率,通过滤波所得到的航路,可以看出激光回波率对目标航路测定的影响,如图9所示。
针对航路三,采取不同的回波率,可得在不同情况下跟踪性能指标CRLB 下界与λ 的关系,如图10所示。

图9 激光回波率对目标航路测定的影响(航路三)Fig.9 Effect of laser echo rate on target measurement in airway 3
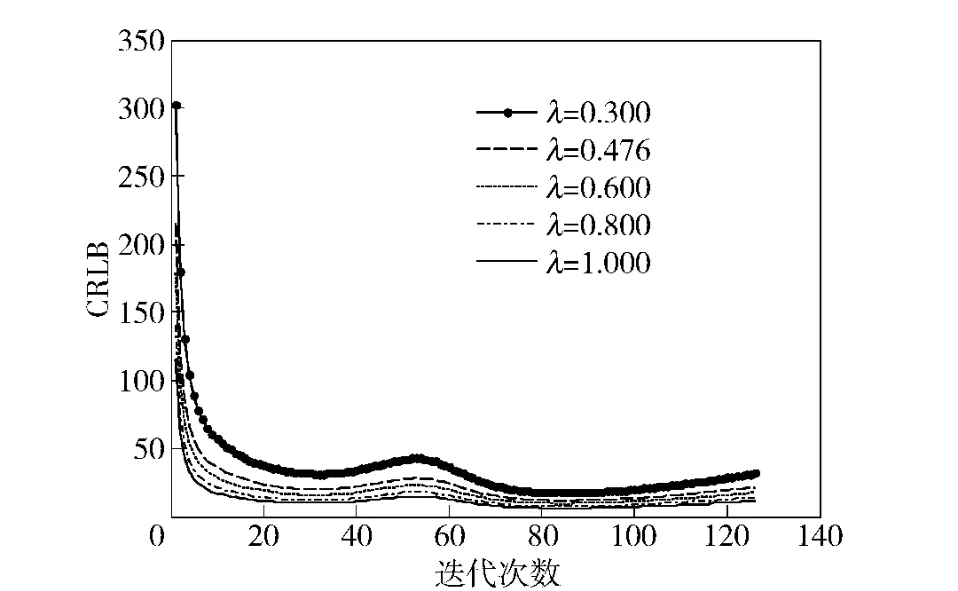
图10 回波率与CRLB 关系(航路三)Fig.10 Relationship between laser echo rate and CRLB inairway 3
通过光电跟踪系统对3 条不同航路进行仿真比较,从图3、图6、图9中可以看出,当λ=0.7,0.9时,3 条滤波所得的航路都能够很贴切的逼近目标运动轨迹;当λ=0.5 时,滤波所得的航路与目标运动轨迹虽然都有稍许的偏差,但并不会发散;当λ=0.3 时,滤波航路与目标运动轨迹都有较大的偏差,滤波所得的航路完全偏离了实际目标的运动轨迹。因此可以看出,当激光回波率高于回波率下界时,都能取得有效的滤波航路,反之可能发散,滤波无效。以上3 条滤波航路所求的回波率下界都低于50%,因此在工程中,往往取激光回波率远高于50%,就能够确保滤波所得航路的收敛,滤波有效。
同样,从图4、图7、图10中,可以看出,当λ=1时,即为完全量测情况的下的跟踪滤波,此时,目标跟踪系统的误差方差的下界最小;而当λ=0.6 和λ=0.8 时,误差方差的下界大于完全量测情况,但相差较小;而当λ=0.3 时,可以看出系统的误差方差下界远大于完全量测的情况,滤波误差较大。可以得出,当激光回波率越低,跟踪系统的误差方差的下界就越大,系统的跟踪性能越差。因此,在工程成本和条件的允许下,回波率越高,滤波的效果越好。
4 结论
本文依据不完全量测理论,定义了能够建立有效航路的激光回波率下界,并将该下界表示为一个非线性不等式的最优解形式,对实际工程应用具有一定的指导作用,避免了在设计工作中的盲目性。对跟踪系统在3 种场景下的回波率下界进行计算可知,回波率下界均小于50%.由此可知当跟踪系统的回波率高于50%时,跟踪系统统计意义下的估计误差协方差对任意估计初值均收敛;反之,可能发散。同时,分析了在不同激光回波率下跟踪系统的估计性能的差别,可知当激光回波率越高,系统的跟踪精度越高。通过工程应用,也证明了本文的结论具有实际参考作用。
References)
[1] 盛安冬,吕太全,殷开宝,等.激光导向伺服系统中满意PID调节器的LMI 设计[J].兵工学报,2002,23(4):485-488.SHENG An-dong,LÜ Tai-quan,YIN Kai-bao,et al.LMI design of satisfactory PID controller in a laser oriented servo system[J].Acta Armamentarii,2002,23(4):485-488.(in Chinese)
[2] 程相权,郭治,王远钢,等.满意估计下的激光回波率研究[J].兵工学报,2002,23(3):332-335.CHENG Xiang-quan,GUO Zhi,WANG Yuan-gang,et al.A study on laser echo rate based on satisfaction estimation[J].Acta Armamentarii,2002,23(3):332-335.(in Chinese)
[3] Farina A,Ristic B,Timmoneri L.Cramer-rao bound for nonlinear filtering with Pd <1 and its application to target tracking[J].IEEE Transactions Signal Processing,2002,50(8):1916-1924.
[4] Sinopoli B,Schenato L,Fransceschetti L M,et al.Kalman filtering with intermittent observations[J].IEEE Transactions on Automatic Control,2004,49(9):1453-1464.
[5] Hassibi A,How J,Boyd S.A path-following method for solving BMI problems in control[C]∥Proceedings of American Control Conference.San Diego:1999:1385-1389.
[6] Sinopoli B,Mo Y.A characterization of the critical value for Kalman filtering with intermittent observations[C]∥Proceedings of the 47th IEEE Conference on Decision and Control.Cancun:2008:2692-2697.
[7] Boers Y,Driessen H.Results on the modified Riccati equation:target tracking applications[J].IEEE Transactions on Aerospace and Electronic Systems,2006,42(1):379-384.
[8] Plarre K,Bullo F.On Kalman filtering for detectable systems with intermittent observations[J].IEEE Transactions on Automatic Control,2009,54(2):386-390.
[9] Huang M,Dey S.Stability of Kalman filtering with Markov packet losses[J].Automatica,2007,43(4):598-607.

