量子粒子群算法的弹载SAR 图像自聚焦方法

谭覃燕，宋耀良

(南京理工大学 电子工程与光电技术学院，江苏 南京210094)

合成孔径雷达(SAR)具有全天时全天候工作、穿透性好、高分辨率成像的特点。如果能通过装载在导弹上的SAR 获取目标或目标附近典型地貌特征，从而控制导弹精确命中目标，可以大大提高导弹的攻击能力［1］，具有重要的军事意义。美国、俄罗斯、德国等都开展了SAR 导引头方面的研究。与机载SAR 对地面目标成像不同，弹载SAR 对目标成像具有平台运动速度快、非匀直线运动和大斜视角三大特点。对成像算法的实时性、运动补偿的精度和横向分辨率都提出了更高的要求。由于弹载SAR 运动误差引起的相位误差较大，传统的成像算法如距离多普勒算法(RD)、线频调变标算法(CS)、距离徙动算法(RMA)等在进行运动补偿后，成像效果都不太理想，往往还要求通过自聚焦方法从SAR回波数据中估计并补偿残余的相位误差。

SAR 成像中常用的自聚焦算法有子孔径算法(Map-Drift)、对比度算法、相位梯度法(PGA)［2］等。子孔径算法和对比度算法运算量相对较小，对二次相位误差的估计比较稳健，缺点是随着相位误差的增大估计精度降低。PGA 方法不需要指出待估计相位误差的最高阶数，并且能够用于大多数成像场景，因此，自其出现以来，在SAR 领域得到了广泛应用。PGA 算法通过迭代逐步进行相位误差校正，它往往需要在图像中存在孤立的强点目标，因此对于没有任何孤立强点目标的场景并不是很理想。

将一种基于群体智能的随机搜索算法——量子粒子群(QPSO)算法应用于弹载SAR 成像自聚焦，并根据弹载SAR 回波信号和成像的特点对QPSO算法进行了改进，由此提出了基于QPSO 算法的自聚焦方法，将这种新算法应用于弹载SAR 回波的成像。该方法是基于非参数相位误差的估计，以最小熵准则作为评判标准，对基于运动传感器的运动补偿以后的残留相位误差以及其他原因造成的相位误差进行补偿，具有较好的鲁棒性和收敛速度快的特点。该方法无需像PGA 算法那样在图像域分离出强点目标，因而适用于绝大多数场景，特别是对于无任何明显特征的图像，其聚焦效果好于PGA.仿真处理结果证明了该方法的有效性。

1 弹载聚束SAR 成像模型的建立

导弹和成像目标区域的几何关系如图1所示。图中:v、a 为导弹飞行的速度和加速度;α、β 为速度和加速度与天线指向间的夹角;φ 为天线波束相对地面的入射角;R(t)为雷达与目标之间的瞬时距离。导弹发射后，首先通过发射窄带信号自动搜索、锁定并跟踪地面目标。当导弹与目标的相对距离达到一定距离时，进入末制导阶段。此时发射宽带信号，开始进行SAR 成像处理。

图1 弹载SAR 对地面目标成像几何关系图Fig.1 Geometry for missile-borne SAR imaging

末制导阶段由于导弹的非匀直运动，使其沿弧线飞行，在t 时刻，导弹与目标间的瞬时距离为

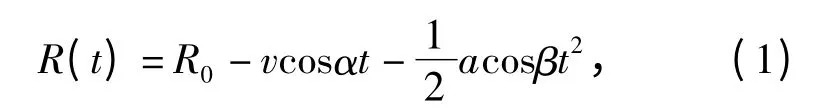
式中R0为雷达与目标之间的初始距离。设一次成像所要求的相干处理时间为Ts，在此期间，导弹相对于目标转过的角度为

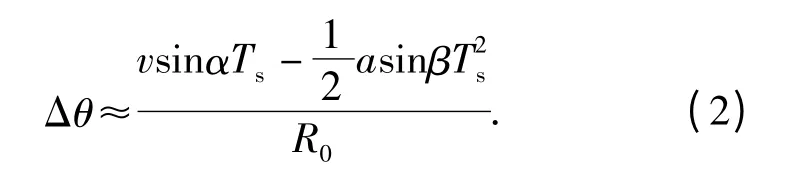
一般情况下，导弹飞行轨迹受最大法向过载限制，因此在成像期间导引头转过的角度不能过大。

合成孔径时间为

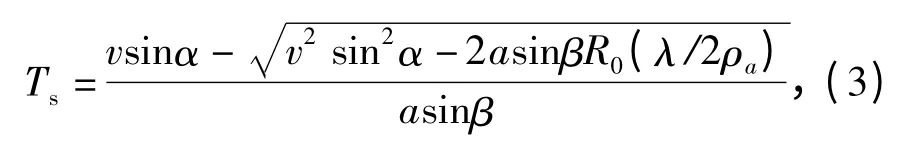
式中λ 为雷达工作波长。在一次相干处理时间内，目标相对雷达的距离走动为

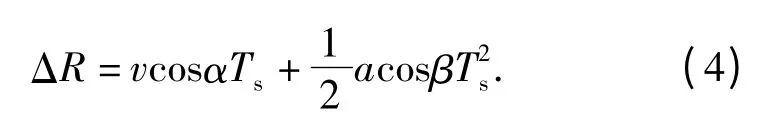
选取一组典型的参数:R0=8 km，v=500 m/s，α=15°，β=5°，λ=3 cm，ρa=5 m，a=10 m/s2，可算出Ts=185.6 ms，Δθ=0.003 rad，ΔR=89.8 m.

在实际系统中，导弹的运动会受到大气气流等因素的影响，产生的扰动使得天线不一定总指向成像区域。另外，虽然Δθ 很小，造成成像时间很短，但导弹的运动速度快，在很短的成像时间内仍能使相对目标的径向移动远远大于半个距离分辨单元。当雷达和目标间的相对运动引起的距离变化超过半个距离分辨单元时，必须进行相位补偿，否则无法成像。在传统的成像算法中，相位补偿通过在整个回波上乘上一个相位补偿因子来完成，但由于存在近似，距离徙动校正不完全，方位向匹配滤波函数存在相位误差，使得散射点图像存在比较严重的散焦。因此，为得到聚焦良好的图像，在传统的运动补偿后，高分辨率成像往往还要求从SAR 回波数据中自动估计并补偿残余的相位误差，这一过程称为自聚焦。

2 相位误差模型

相位误差可分为低频相位误差、高频正弦相位误差和宽带相位误差［3］。它们对图像造成的影响如表1所示。

高频正弦相位误差是由于天线相位中心(APC)未被补偿掉的振动造成的，宽带相位误差产生于随机运动测量误差，它们都属于高频相位误差。在弹载SAR 系统中，通过惯性测量单元(IMU)和全球定位系统(GPS)的结合可以精确的测定APC 的结构运动以及其他高频运动，因此在运动补偿阶段，可以较好的补偿掉高频相位误差，采用的自聚焦算法主要是针对未补偿掉的低频相位误差。

表1 相位误差及其影响Tab.1 Phase error and its effects

低频相位误差的周期比合成孔径时间大得多，它主要是由于速度和加速度测量误差以及成像算法上的近似造成的，经泰勒级数展开，包括线性相位误差(一阶)、二阶相位误差(QPEs)和高阶相位误差，可用K 阶多项式的形式来描述方位向低频相位误差

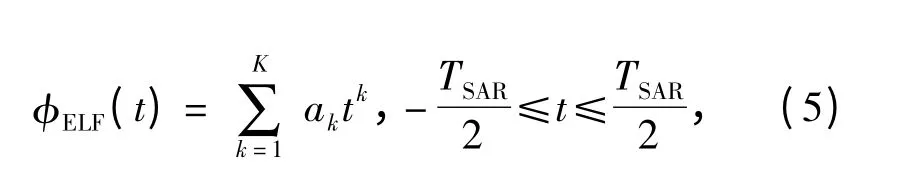
式中:ak为K 阶多项式的系数;TSAR为合成孔径时间。其中线性相位误差项只造成整幅图像的偏移，不影响图像的聚焦效果。低频相位误差主要影响系统冲击响应的主瓣，使图像产生几何失真，分辨力损失。一般的自聚焦算法只将低频相位误差近似到慢时间的二次相位项，但对于弹载SAR 来说，由于弹载雷达斜视角较大，慢时间的高次相位误差项对成像影响较大，所以不能忽略它。

为了使相位误差最小化，自聚焦算法的任务是从方位向回波数据中找到相位误差的最佳估计值。因此对相位误差的估计问题可转化为非线性最优估计问题。本文提出基于QPSO 算法的自聚焦方法很好的解决了小信噪比、地面反射目标情况复杂、相位误差函数有多个极值情况下的复杂自聚焦问题，而这些问题利用传统的自聚焦方法是很难解决的。

3 基于QPSO 算法的自聚焦方法

3.1 PSO 算法

粒子群算法(PSO)［4］是一种新的基于群体智能的全局优化算法，它源于对鸟类捕食行为的模拟。PSO 算法将每个粒子看作是在n 维搜索空间中的一个没有质量和体积的微粒，并在搜索空间中以一定的速度飞行。该飞行速度由粒子的飞行经验和群体的飞行经验进行动态调整。

设每个粒子处于D 维空间中，xi=(xi1，xi2，…，xim)为粒子i 的当前位置;vi=(vi1，vi2，…，vim)为粒子i 的当前飞行速度;pi=(pi1，pi2…，pim)为粒子i所经历的最好位置，也就是粒子i 所经历过的具有最好适应值的位置，称为个体最好位置(pbest).

标准PSO 的进化方程可描述为

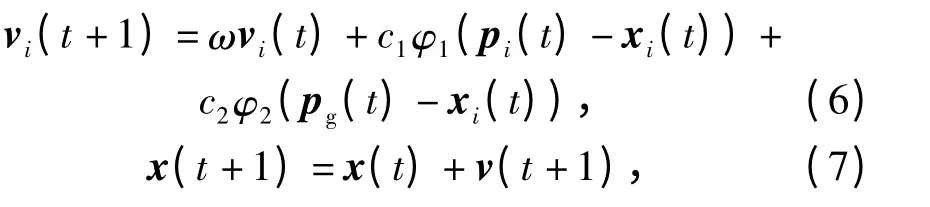
式中:t 为迭代次数;φ1和φ2为［0，1］范围内变化的随机数;ω 为惯性权重因子;c1，c2为加速常数，分别调节向个体极值和全局极值方向飞行的步长。pg为所有微粒中最优微粒的位置，记为gbest.算法的核心思想是通过跟踪粒子当前的局部最优解和全局最优解来更新粒子的速度和位置，当达到终止条件时，当前的全局最优解即为该问题的最优解。

3.2 QPSO 算法［5］

在标准PSO 粒子群系统中，粒子的搜索空间是一个有限的区域，不能保证以概率1 收敛到全局最优解，这正是其最大的缺点。根据粒子群的基本收敛性质，受量子物理基本理论的启发，Sun 等［6］提出的QPSO 算法进化方程中不需要速度向量，进化方程的形式更简单、参数更少且更容易控制。它可以在整个可行解空间中进行搜索，因而QPSO 算法的全局搜索能力远远优于标准的PSO 算法。在量子空间中，粒子的速度和位置是不能同时被确定的，因此文献［6］通过波函数ψ(x，t)(其物理意义为:波函数的平方是粒子在空间某一点出现的概率密度)来描述粒子的状态，并通过求解薛定谔方程得到粒子在空间某一点出现的概率密度函数。随后通过蒙特卡罗随机模拟的方式得到粒子的位置方程为

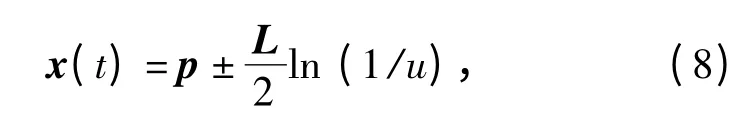
u 为［0，1］范围内变化的随机数，L 被定义为

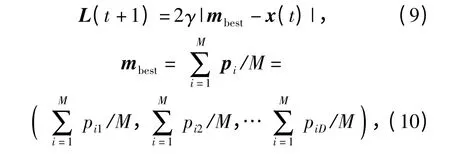
式中:γ 为收缩扩张系数，用来控制算法的收敛速度;mbest为中值最优位置;M 为粒子的数目;D 为粒子的维数;pi为第i 个粒子的pbest.最后得到粒子的位置方程为

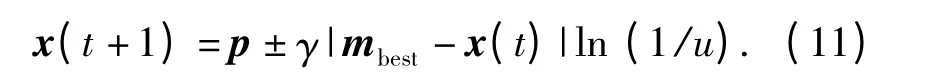
由上述可知，QPSO 的状态只需要用位置向量来描述，并且只用一个参数γ 决定粒子的收敛速度和位置，与PSO 算法需要用参数c1、c2、ω 相比，具有参数少，编程简单，易实现和收敛速度快的优点，能更快的在全局范围找到最优解。

3.3 基于QPSO 算法的自聚焦方法设计

散焦的SAR 图像可以看作是清晰图像与相位误差造成的点扩散函数卷积的结果，如图2所示。

图2 图像散焦等效模型Fig.2 Equivalent model of image defocusing

根据上面的模型，自聚焦算法可归结为系统冲激响应，这是一个典型的盲解卷积问题。Shalvi等［7］证明了利用最小熵准则盲解卷积在大多数条件下能收敛到正确结果，提前条件是要求数据服从非高斯分布及传输函数无零点。

SAR 原始数据是来自大量独立散射体的回波信号的总和，SAR 图像是成像目标散射系数的反映。在高分辨力情况下，各分辨单元内散射体个数有限，大数定律不成立，因此，各分辨单元的散射系数呈非高斯分布。但对传输函数无任何先验知识，为此采用基于群体智能的QPSO 搜索算法实现最小熵准则解卷积，即在相位误差估计的区间范围内搜索最小熵值所对应的相位误差，随后的仿真处理结果验证了该方法的有效性。

图像熵有2 种定义方式:Shannon 熵和Renyi熵。在这里采用Shannon 熵的定义方法。最小熵准则自聚焦算法从复图像域出发，这意味着与采取哪种算法实现成像无关，经方位向逆傅里叶变换回到距离压缩相位历史域。包含相位误差的距离压缩相位历史域数据可写成如下形式

式中:F(x，t)为理想的距离压缩相位历史域数据;φe(t)为要搜索的相位误差，它对所有距离单元都是相同的。变量x 和t 分别表示距离向坐标和方位向慢时间坐标。距离压缩相位历史域与图像域呈傅里叶变换关系，将(12)式对方位慢时间t 做傅里叶变换可以得到受相位误差干扰的图像

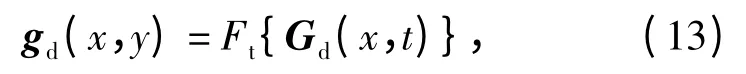
式中y 为方位向坐标。利用QPSO 自聚焦方法估计得到的相位误差^φe(t)对距离压缩相位历史域数据进行校正，可得到

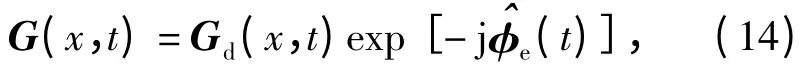
相应的相位误差校正后的图像为

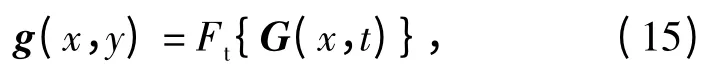
因此可以得到一幅复SAR 图像G 的Shannon 熵为

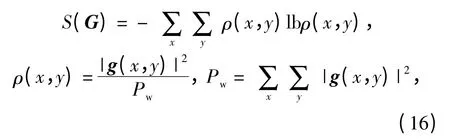
式中:S(G)、ρ(x，y)、g(x，y)、Pw分别为图像的熵、各像素功率在图像总功率中的比例、像素值、像素总功率。

当SAR 图像聚焦效果越好时，谱峰越尖锐，则图像的熵就越小。所以当图像的熵取最小时，聚焦效果最好，相位误差补偿最精确。以熵作为衡量相位误差估计准确程度的代价函数，通过多维搜索完成相位误差校正。

QPSO 自聚焦算法的目标函数和相位误差系数如表2所示。在低频相位误差中，二次相位误差系数反映了导弹速度的偏差，据此可估算二次相位误差系数的大致范围;三次以上高阶相位误差通常小于二次相位误差，相应地确定了各次相位误差系数的取值区间，根据经验值，设ak为［-50，50］区间。

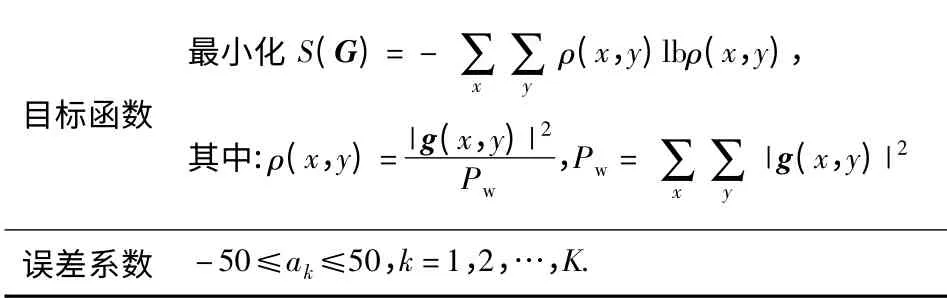
表2 QPSO 自聚焦算法的目标函数和误差系数Tab.2 Objective function and error coefficients of QPSO auto-focusing algorithm

目的是在低频相位误差φELF的可行解空间中找到使图像熵值最小的，并以此作为φELF的最佳估计值。具体的实现如下:

1)产生一定数目的个体(粒子)组成种群，其中不同的个体代表一个不同的相位误差的估计值。初始化粒子群，根据相位误差的搜索范围设定各个粒子的随机初始位置;同时初始化pi和pg.

2)对每一个粒子，分别计算适应值(图像的熵)。将其适应值与其本身所经历过的最好位置pi的适应值进行比较，如果当前适应值比前面的值小，就把当前位置xi作为新的pi，即如果f(Xi)＜f(pi)，则pi=xi.

4)比较当前的全局位置和前面的全局位置;如果当前全局位置的适应值小于前面的值，那么将当前全局位置设为全局位置。

5)对于粒子的每一维，从pid和pgd中取随机的一个点:p=(φ1pid+ φ2pgd)/(φ1+ φ2)其中φ1=rand(0，1)，φ2=rand(0，1).

6)通过下面的随机公式来获得一个新的位置:

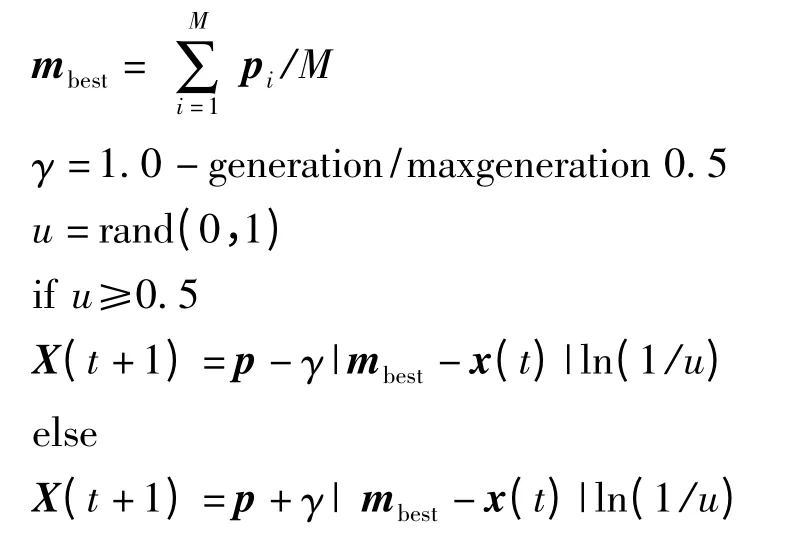
其中:u 为0 至1 之间的随机数;mbest为粒子群pbest的中间位置，即平均值;γ 为收缩扩张系数，在QPSO收敛过程中线性减小;generation 为当前进化代数;maxgeneration 为设定的最大进化代数。

7)判断是否满足算法终止的条件。如不满足则按照QPSO 算法模型生成新的粒子，并转到步骤2);如满足则输出一组具有最优适应值的参数作为低频相位误差的估计，算法结束。算法终止的条件可以有2 种选择:1)当适应值最小的粒子不再发生变化时，将此粒子所代表的相位误差的估计值作为最后的相位误差估计，算法终止;2)可以规定算法的迭代次数大于某一正整数时算法终止。

4 仿真分析与仿真结果

假设导弹攻击目标由若干个强散射点组成，其分布如图3所示。

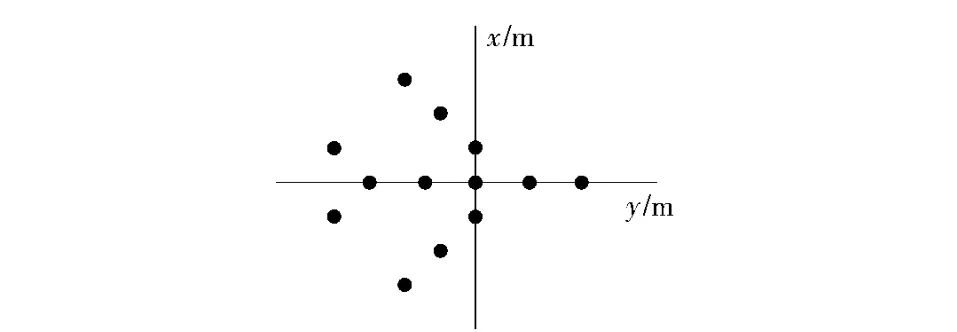
图3 目标散射点分布Fig.3 Distribution of scattering points

设雷达发射线性调频信号

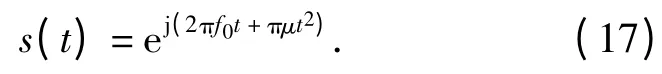
点目标雷达回波为

由(1)式，有

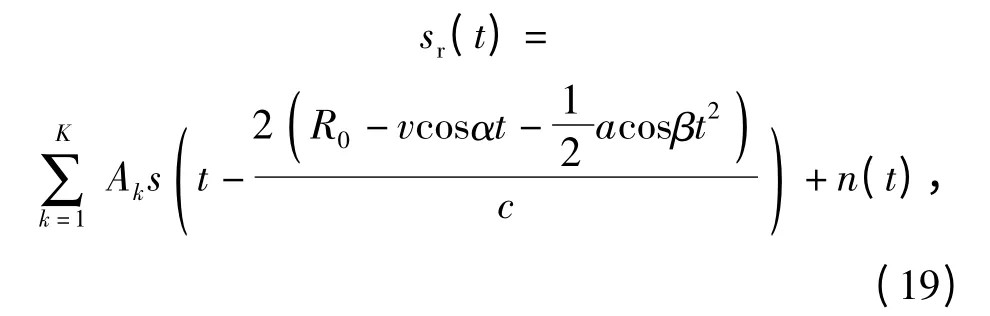
式中:n(t)为加性高斯白噪声，设置信噪比为20 dB，用以上雷达回波方程对点目标进行仿真。

利用表3给定的系统参数，给出计算机仿真结果。

表3 仿真参数Tab.3 Simulation parameters

由于线性相位误差只是造成图像的整体平移，对图像结构没有影响，在此不予考虑，线性相位误差项系数a1设置为0.传统的自聚焦算法，如子孔径相关法、对比度算法等，对二次相位误差(QPEs)的估计比较稳健。在此主要测试该方法对于复杂情况下低频高阶相位误差的补偿性能，该相位误差利用传统的自聚焦方法很难补偿。二次相位误差项系数反应了导弹在飞行过程中速度的偏差，根据经验值，导弹飞行速度的偏差设定为［-50 m/s，50 m/s］范围，所以a2设定为21，而三次以上高阶相位误差通常小于二次相位误差，所以高阶相位误差系数设置为-50 ＜ak＜50.在距离压缩相位历史域，可合理假设引入相位误差φe(t)如表4所示。

用距离—多普勒算法进行成像处理，图像大小为2 048 像素×2 048 像素。图4(a)为原始弹载SAR 图像某距离单元的一维仿真结果，在没有任何相位误差干扰的情况下，它的能量高度集中，主瓣很窄且远远高于旁瓣，可以很容易的把各点目标区分开来。由于导弹的非匀直运动，回波中将不可避免的存在较大的相位误差。在图4(a)中引入如表4所示的相位误差后，由于距离压缩相位历史域与图像域呈傅里叶变换关系，因此该目标受点扩散函数的影响而散焦，表现为主瓣展宽、峰值降低、旁瓣电平增高等，如图4(b)所示。采用QPSO 自聚焦算法对散焦图像进行处理，QPSO 算法的迭代次数可以有2 种选择:1)根据相位误差的经验值设置最大迭代次数，当达到最大迭代次数时，循环终止。2)本次估计相位误差与上次估计相位误差的差值小于某一设定的值ε 时，循环终止。本文选择的是第1 种方式。QPSO 算法的参数设置如下:粒子数取50，最大进化代数为20 代，收缩扩张系数β 在一次运行中由1.0 线性递减为0.5.处理的结果如图4(c)所示，从图中可以看出，成像效果得到明显的改善，旁瓣电平得到明显的抑制，各点目标的峰值基本恢复到了原始的幅值。为了与传统的自聚焦方法进行对比，选用PGA 自聚焦算法对散焦数据进行处理，经过20 次迭代后得到如图4(d)所示的结果，虽然聚焦效果得到一定的改善，但还存在较高的旁瓣电平，会把一些弱目标淹没掉。

表4 相位误差Tab.4 Phase error

图5(a)为相应的原始弹载SAR 图像，图5(b)为受相位误差干扰的图像，耦合相位误差后，在方位向出现了明显的散焦现象，点目标已经无法分辨。图5(c)、(d)分别为经过QPSO 自聚焦算法和PGA自聚焦算法处理后的图像，对比这2 幅图像可以看出，QPSO 自聚焦算法的聚焦效果优于PGA 自聚焦算法。

针对以上仿真，从量上对以上过程进行了分析，结果如表5所示。

表5所给出的结果说明在以图像熵为评判标准的情况下，QPSO 自聚焦算法对图像的聚焦程度比PGA 自聚焦算法好。在迭代过程中，图像熵的收敛曲线如图6所示。从图(6)可以看出，QPSO 自聚焦算法聚焦性能和收敛速度明显优于传统的PGA 自聚焦算法。

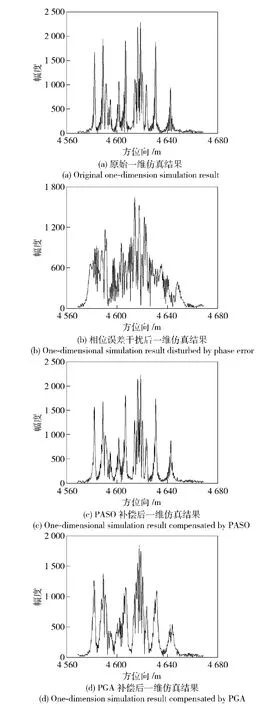
图4 某距离单元自聚焦性能比较Fig.4 Auto-focus ability of a range cell

图(7)为QPSO 和PGA 自聚焦算法分别对其中某一单点目标的成像处理结果。

图5 成像效果比较Fig.5 Comparison of image results

表5 仿真结果Tab.5 Simulation results

图6 图像熵的收敛曲线Fig.6 Convergence curves of IE

图7 点目标图像比较Fig.7 Comparison of point target images

图(8)为QPSO 和PGA 自聚焦算法处理后该单点目标的距离向和方位向剖面图。从图中可以看出，QPSO 自聚焦算法的聚焦程度和点目标的旁瓣性能都优于PGA 自聚焦算法。

表6分别从方位向和距离向的空间分辨率、峰值旁瓣比、积分旁瓣比方面对2 种自聚焦方法进行了比较。

讨论了这2 种自聚焦方法对于信噪比的适应能力。图10给出信噪比SNR=-3 dB 时，2 种算法对相位误差的估计程度。从图中可见QPSO 算法得到的相位误差估计性能比PGA 算法好。

图11进一步给出了在不同信噪比下2种算法对相位误差的估计性能。随着信噪比的增大，2 种算法对于相位误差估计的准确程度都提高，但QPSO算法在低信噪比的情况下，对相位误差估计的准确程度明显优于PGA 算法。

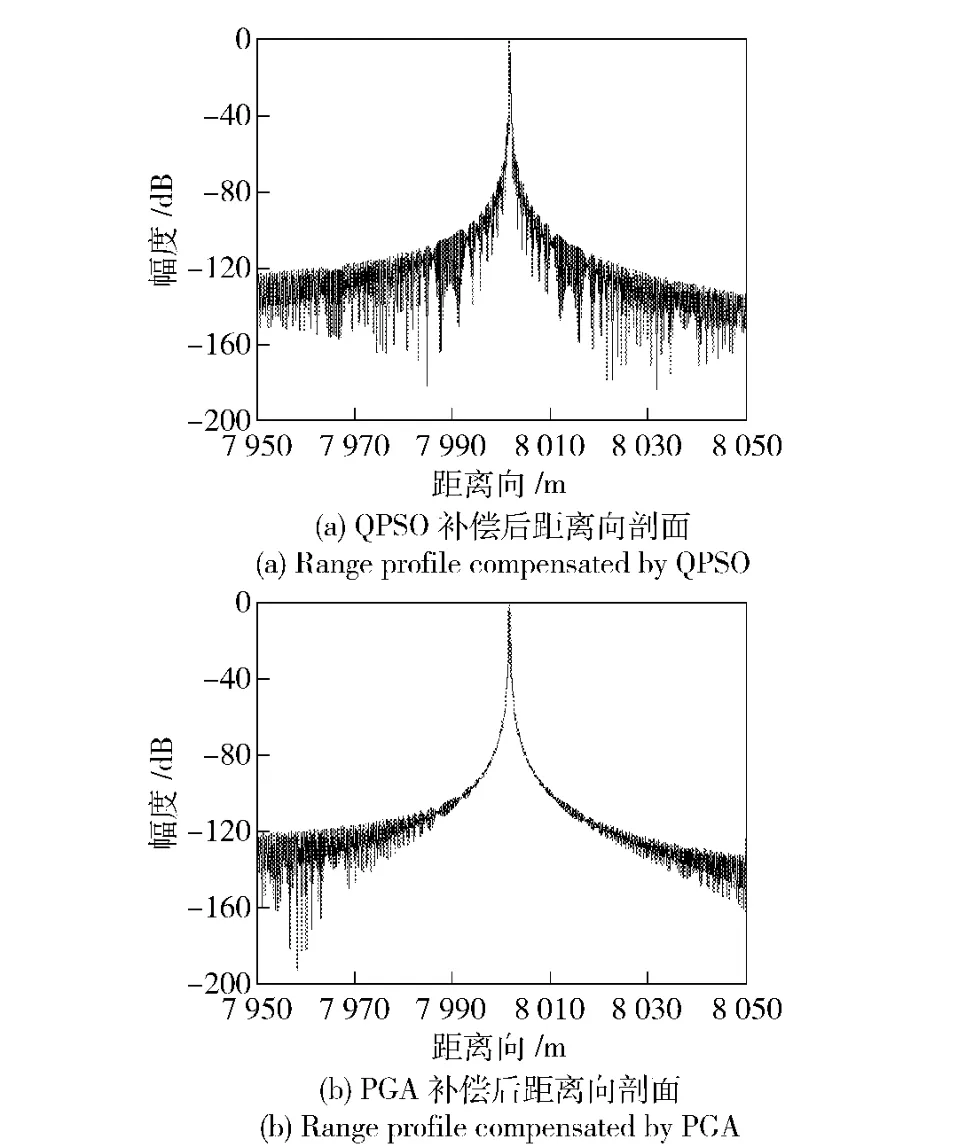
图8 距离向剖面图Fig.8 Range profile

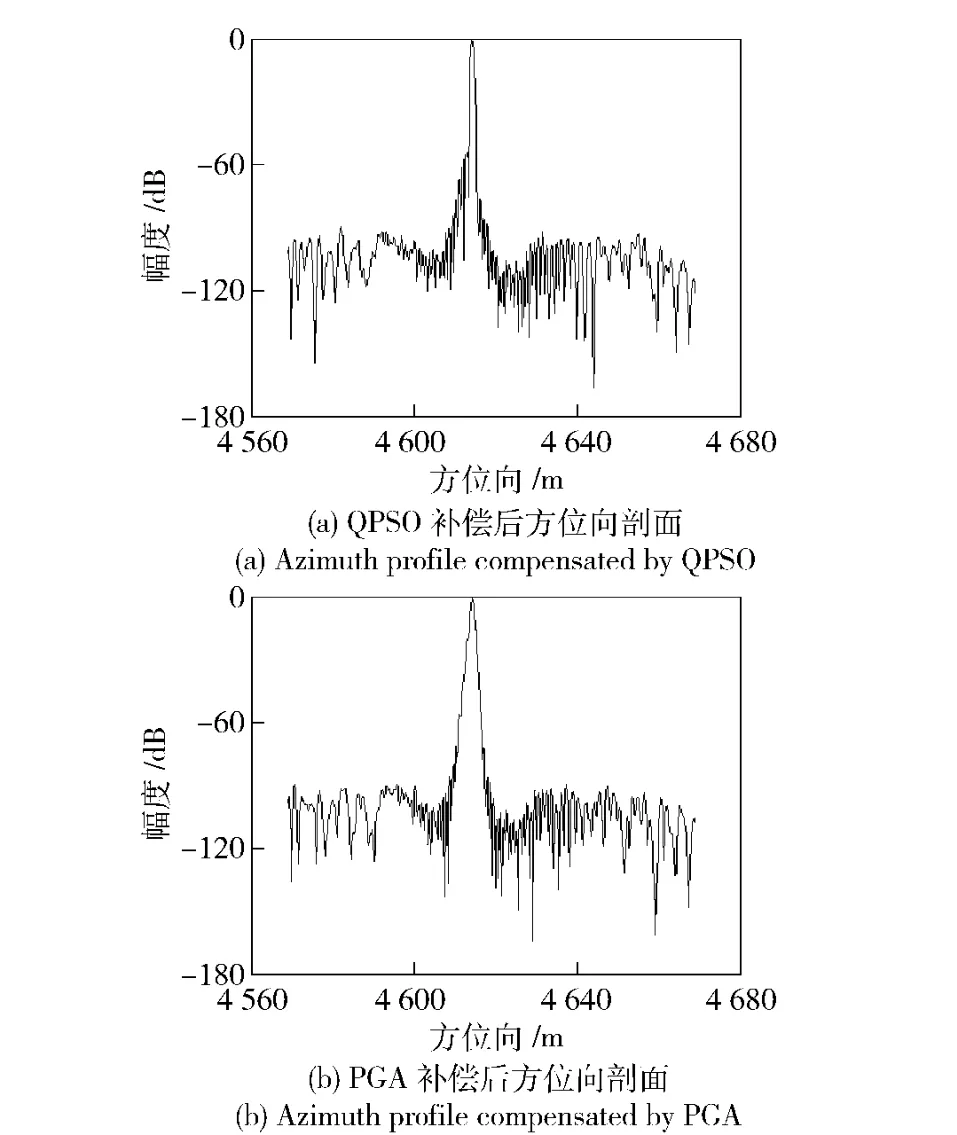
图9 方位向剖面图Fig.9 Azimuth profile

表6 图像质量测量结果(多点测量的平均值)Tab.6 Image quality

图10 SNR 为-3 dB 时2 种算法性能比较Fig.10 Comparison of two algorithms in SNR of-3 dB

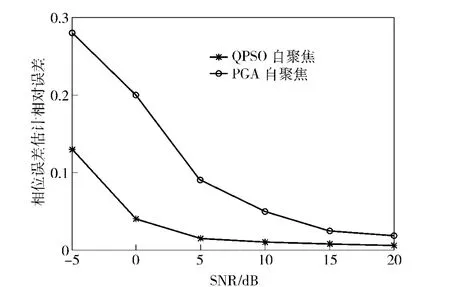
图11 相位误差的估计误差Fig.11 Estimation error of phase

5 算法复杂度分析

算法复杂度是SAR 成像处理的一个重要因素，尤其是实时成像处理，要求尽可能减小计算量。因此分析了本文QPSO 自聚焦算法的复杂度，并且与PGA 算法作了比较。图像方位长M=2 048，选取N=64 条一维图像作估计。计算量按复数乘法或加法的次数计。

分析QPSO 自聚焦算法每次迭代的计算量。每次迭代的主要计算量是作一次成像处理和计算图像的熵。其中成像处理包括:1)方位向IFFT 回到距离压缩相位历史域，计算量为(3/2)MNlbM=2 162 688.2)补偿相位误差与距离压缩相位历史域数据相乘，计算量为MN=131 072.3)方位向FFT回到复图像域，计算量为(3/2)MNlbM=2 162 688.计算图像熵的计算包括取绝对值、求和，乘法运算，平方运算等，计算量约为7MN=917 504.粒子产生、更新的计算量与以上相比很小，可以忽略。一次迭代的总的计算量约为3MNlbM+8MN=5 373 952，因此一次迭代的计算量阶次为O［3MNlbM］.

PGA自聚焦算法的每次迭代包括:1)找出方位向幅度最大的散射点并圆周移位到图像的中心，再作加窗处理。2)作FFT，计算出相位梯度PG=3)计算相位误差并作补偿。4)作IFFT 得到图像。

选取方位向能量分布图的峰值位置下降至-10 dB 处所对应的主瓣宽度为窗口宽度，窗函数中心为图像中心。当相位误差小于门限ε=0.001π 时，退出循环。计算PGA 自聚焦算法的幅度要做MN 次运算，圆周移位的计算量可以忽略，加窗计算量为MN，总共2MN=262 144;作FFT 运算量为(3/2)·MNlbM=2 162 688，计算相位梯度计算量约为5MN=655 360;计算相位误差并作相位误差补偿运算量约为MN=131 072;做IFFT 运算量为(3/2)MNlbM=2 162 688.总的计算量约为3MNlbM+ 8MN=5 373 952，一次迭代的计算量阶次为O［3MNlbM］.

用MATLAB 仿真，QPSO 自聚焦和PGA 自聚焦实现一次循环需要的计算时间分别为5.158 s 和5.344 s.可见，QPSO 自聚焦算法一次迭代的计算量与PGA 自聚焦算法相当，但QPSO 自聚焦算法收敛速度和聚焦性能都好于PGA 自聚焦算法，所以从总体上来说，QPSO 自聚焦算法要优于PGA 自聚焦算法。

6 结论

利用最小熵准则作为评判标准，提出了一种基于QPSO 算法的自聚焦方法，用来提高弹载SAR 的打击精度。该算法可以用来估计任意阶的相位误差，不依赖于场景中存在强点目标，无论从收敛速度还是聚焦性能来说，都优于传统的PGA 自聚焦方法，有着良好的应用前景。

References)

［1］ 俞根苗，尚勇，邓海涛，等.弹载侧视合成孔径雷达信号分析及成像研究［J］.电子学报，2005，33(5):778-782.YU Gen-miao，SHANG Yong，DENG Hai-tao，et al.Signal analysis and imaging processing of missile-borne side-looking SAR［J］.Acta Electronica Sinica，2005，33(5):778-782.(in Chinese)

［2］ Wahl D E，Eichel P H，Ghiglia D C，et al.Phase gradient autofocus-a robust tool for high resolution SAR phase correction［J］.IEEE Trans on AES，1994，30(3):827-834.

［3］ Carrara W G，Goodman R S，Majewski R M.Spotlight synthetic aperture radar signal processing algorithms［M］.Boston:Artech House，1995.

［4］ Jin Nanbo，Yahya Rahmat.Advances in particle swarm optimization for antenna designs:real-number，binary，single-objective and multi-objective implementations［J］.IEEE Trans on Antennas and Propagation，2007，55 (3):556-567.

［5］ Said M Mikki，Ahmed A Kishk.Quantum particle swarm optimization for electromagnetic［J］.IEEE Trans on Antennas and Propagation，2006，54(10):2764-2775.

［6］ Sun J，Feng B，Xu W.Particle swarm optimization with particles having quantum behavior［C］∥Proceedings of 2004 Congress on Evolutionary Computation.Portland:2004:325-331.

［7］ Shalvi O，Weinstein E.New criteria for blind deconvolution of nonminimum phase systems［J］.IEEE Trans on Inform Theory，1990，36(3):312-321.