枪械自动机冲击疲劳试验机加载机构设计优化及性能分析
何玲,徐诚
(南京理工大学 机械工程学院,江苏 南京210094)
自动机是枪械的核心部件,其主要承力构件的寿命问题一直受到广泛关注。我国现在装备的枪械中许多自动机主要承力构件的寿命低于全枪寿命,必须配备备份件[1]。自动机关重件工作时主要承受冲击载荷,其破坏属于冲击疲劳破坏。因此,为研究冲击载荷下自动机关重件的损伤、疲劳寿命及失效的规律、机理、影响因素和控制方法,研制自动机关重件冲击疲劳试验机具有重要意义[2]。
目前美国、日本、欧洲等国家和地区研制的冲击试验机水平较高,而国内冲击试验机的研制起步较晚,产品结构上基本相近于国外同类产品,但质量上存在一定差距。国内外冲击试验机大多数属于单次冲击试验机或是冲击频率、冲击能量较低的多次冲击试验机,也有一些科研机构研制出可进行多次冲击的试验机,如苏州大学研制的多冲碰撞试验机。该冲击试验机能够提供较大的冲击速度或冲击能量,但冲击频率较低[3]。同时这些试验机试验对象大多为民用产品,试件结构较简单、体积较大,不适于自动机关重件的冲击疲劳研究。王学颜对自动武器疲劳强度做了专门研究,但所使用的冲击疲劳试验机冲击脉冲不可调节[2]。目前暂无专用于枪械自动机关重件冲击疲劳研究的试验机,零部件设计过程盲目、费用高。因此,迫切需要研发一种枪械自动机冲击疲劳试验机用于对自动武器关重件进行冲击疲劳试验及实验应力分析。有效地运用冲击疲劳寿命模拟试验与试验应力分析方法,不仅能提高枪械自动机的安全度和可靠性,还能达到降低武器系统复杂性及质量的目的。
在研制冲击疲劳试验机过程中,核心问题是如何解决试验机加载问题。加载机构即要求冲击冲量可调,又要求冲击脉冲幅值和幅宽可调。因此,本文以冲击疲劳试验机的冲击加载机构为主要研究对象,提出一种实现方法,在理论上证明其可行。
1 冲击疲劳试验机加载机构设计
1.1 自动机冲击载荷特性分析
枪械在连续射击过程中,自动机各承载构件受到多种交变载荷作用,并且受高温、交变温度和腐蚀介质的影响。根据武器撞击动力学,自动机关重件几乎都是在撞击状态下完成工作循环过程即能量传递过程的(每发射1 发弹,各机构间将发生数次撞击)。由枪械发射试验可知,机枪、手枪、冲锋枪中膛底最大压力以机枪为大,口径14.5 mm 机枪膛压引起的峰值后坐力能够达到14.85 ×104N.作用在自动机各关重件上的载荷为膛压和撞击力,作用时间从0.5~5.0 ms 不等,冲击冲量最大可达100 N·s以上,最大冲击速度10 m/s 以上。应变率在10-1~102s-1范围内,故闭锁片、击针、击锤等关重件受到的膛压作用力和撞击力均属于冲击载荷。由于撞击载荷作用时间短,膛压载荷上升的时间也很短暂,所以冲击疲劳试验中枪械自动机工作过程中所受膛压作用力和撞击力可用脉冲载荷来模拟[1-4]。
目前,测定冲击载荷对零件疲劳强度的影响有2 种方法,即多次冲击试验法和施加平缓的周期性交变载荷法。本试验机拟采用多次冲击试验法,进行零件冲击疲劳试验。目的是考核零件结构抗冲击疲劳能力,找出影响冲击疲劳强度的主要因素。在确定加载方案时尽量考虑按零件实际载荷和受力状况加载,利用脉冲载荷进行冲击模拟加载[2]。因冲击速度较高且冲击冲量较大,如冲击速度完全按真实情况模拟,设计上有一定困难。考虑到冲击是能量载荷,故设计时对冲击速度要求适当降低,通过调整其他变量保证冲击冲量接近真实工况。
1.2 冲击疲劳试验机与加载原理
1.2.1 冲击疲劳试验机
冲击疲劳试验机采用机械式结构,图1(a)为试验机结构简图。试验机机身为C 型开式机身,由驱动、传动、冲击加载等机构组成。图1(b)为冲击加载机构,其结构形式为凸轮滚子机构。图1(c)为力脉冲发生器,发生冲击作用时冲头与试件直接接触,用于提供满足试验要求的冲击脉冲。图中压力簧将力脉冲发生器与顶杆压紧,使之可随顶杆同步运动。在发生冲击时,压力簧能够使脉冲发生器与顶杆脱离。发生器中弹性体用于调整冲击刚度,力传感器可对冲击力脉冲进行精确测量。
1.2.2 冲击加载原理
冲击加载以动量定理为理论依据进行。根据动量定理:物体在一段时间内所受合外力的冲量,等于物体在这段时间内动量的变化,其表达式为

式中:pf为冲击头撞击试样前动量;pa为冲头撞击试样后动量。
因冲击头在冲击作用时间Δt 内质量不变,则动量定理又可写成

式中:m 为冲头的质量;Δv 为冲头撞击前后速度变化量;F 为冲头所受外力,主要包括与试件作用产生的冲击力、碰撞后弹性体变形产生的阻力及其预压力等阻力。
由此可知,冲击动量变化直接导致冲量的变化。而当动量变化一定时,冲击力与作用时间成反比关系。
图2为冲头与试件撞击时,冲头受力情况。为使冲头压紧在脉冲发生器上,发生器中的弹性体在安装时有一个预压缩量,并以预压力的形式一直作用在冲头上,即图中Fp.冲头与试件撞击时,脉冲发生器中弹性体受压缩变形后以阻力Fd作用在冲头上。撞击时受到冲击力Fi的作用。其中,Fp、Fd方向竖直向下,Fi方向竖直向上。
根据动量定理,可得到冲头与试件撞击时的表达式
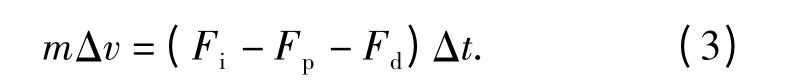
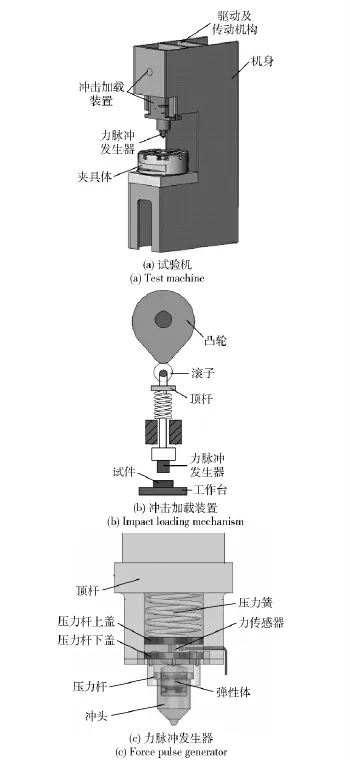
图1 冲击疲劳试验机及主要部件图Fig.1 Impact fatigue test machine and its main assemblies
变换后可得到
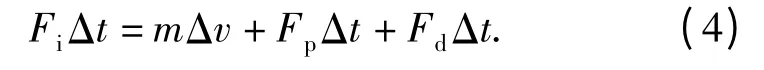
由此可见,冲击冲量与冲头质量、速度变化、弹性体预压力和弹性体变形阻力有关。
根据上式对时间积分就可求出冲击冲量。同时根据赫兹撞击理论,撞击过程可由弹簧及一个与弹簧并联的阻尼器模拟,函数模型[5]
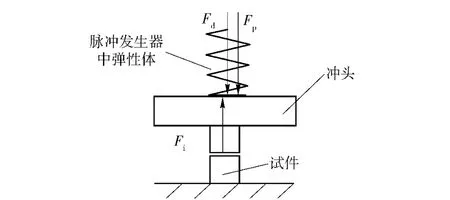
图2 冲头受力情况Fig.2 Force analysis of punch

式中:k 为撞击刚度;s 为两撞击物体之间的瞬时穿透量;e 为非线性作用力指数;c 为阻尼系数;v 为瞬时穿透速度。
由此可见冲击力与以上各参数间的关系,可通过调节这些参数改变冲击脉冲。
1.2.3 结构优化设计
机械优化设计多为对目标函数的优化,而具体问题中的函数类型往往各不相同,实践中人们通常采用具体问题具体分析的方法,采用不同的传统优化算法求解。虽然这些算法经过30 多年的发展,但算法本身的局限性导致了他们普遍存在鲁棒性不强,通用性较差的特点。同时,很多传统算法采用基于梯度进行探索的方法,易陷入局部最优状况。遗传算法是模拟生物在自然环境中的遗传和进化过程而形成的一种自适应全局优化概率搜索算法[6]。遗传算法不依赖于问题模型,寻优过程具有自适应性及隐含的并行性,能够解决复杂非线性问题的鲁棒性,目前已广泛应用于机械优化设计领域。本文使用该方法对凸轮机构进行优化设计计算。
遗传算法以优化变量的编码作为运算对象,同时使用多个搜索点搜索信息,它是基于进化论和遗传学发展起来的一种高效的随机搜索与优化方法。由于传统的遗传算法只能求解无约束极大值问题,所以本文运用遗传算法与罚函数相结合的方法进行优化求解计算。为满足冲击加载机构空间体积最小化及系统惯性最小化要求,运用遗传算法对该凸轮机构进行优化计算。
在优化计算过程中如参数太多或考虑更多的约束条件,人为因素对结果影响愈加严重,同时工作量加大且很难获得结构的最优解。本文以凸轮及滚子的体积V 最小作为目标函数,选择凸轮基圆半径rc、直动从动件滚子半径rr、盘形凸轮轮廓厚度δc作为设计变量。以凸轮机构推程最大压力角不超过许用值,防止轮廓变尖或出现运动失真,保证凸轮运动过程中凸轮副最大接触应力不超过许用值,以及基圆半径rc大于直动从动件滚子半径rr为约束条件。由此得到如下方程组
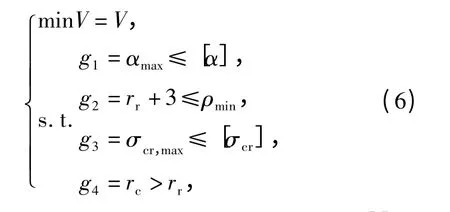
式中:V 为凸轮体积;αmax为凸轮最大压力角;[α]为许用压力角;ρmin为凸轮最小曲率半径;σcr,max为凸轮滚子结构的最大接触应力。凸轮及滚子选用钢制凸轮副,从动件上受到最大载荷为试验机额定载荷Fr,[σcr]为许用接触应力,[σcr]=Sf,lim/Sf,Sf,lim为接触疲劳强度极限。
遗传算法中,为体现染色体的适应能力,引入对问题中每个染色体都能进行度量的函数,即适应度函数。适应度函数要求能够有效反映每个染色体与问题的最优解染色体间的差距。为使寻优过程尽快收敛且不易陷入局部最优解,适应度函数的定义至关重要。
因遗传算法只能求解极大值问题,故本文定义目标函数为
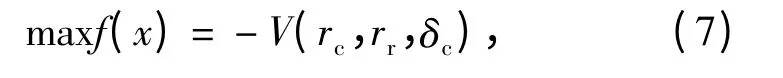
约束条件x∈Q={x∈E4|gi≤0,i=1,2,3,4},E4为自变量可行域。引入罚函数
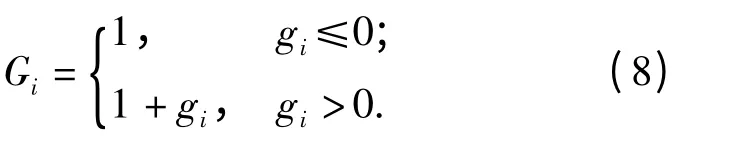
建立适应度函数,
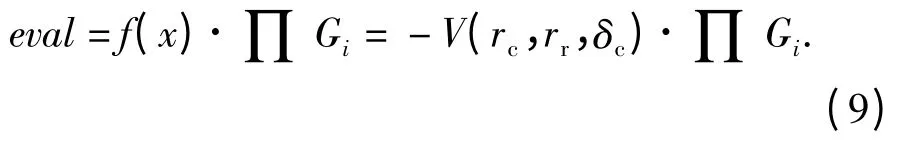
凸轮机构初始参数:rc=101.6 mm,rr=30 mm,δc=20 mm,凸轮及滚子体积为2.588 3 ×105mm3.优化得到结果为rc=100 mm,rr=40 mm,δc=10 mm,凸轮及滚子体积为1.863 6 ×105mm3,比原体积减小28%.
图3为适应度函数值与遗传代数的关系,由图可知适应度函数值在寻优过程中能够稳定且一致地收敛到最优结果。适应度函数从第5 代开始收敛,收敛速度很快,由此说明所选取的适应度函数是合理的。通过对不同组初始串集多次计算,各结构参数收敛趋势和最优解与上述结果一致,可以认为得到的结果是全局最优解。
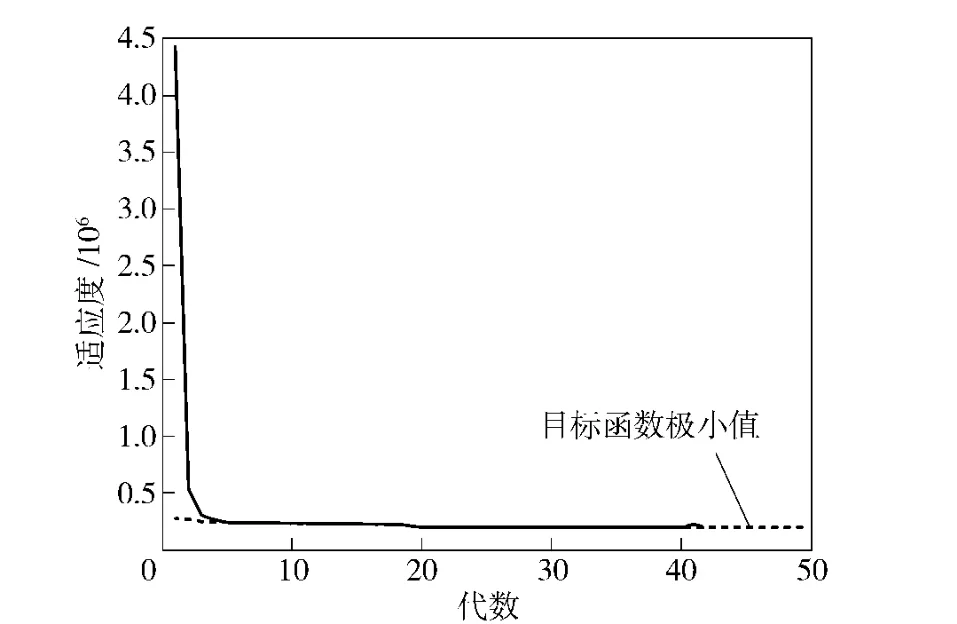
图3 进化曲线Fig.3 Evolutional curve
2 冲击加载机构性能仿真
自动机冲击疲劳试验关键问题在于实现冲击冲量、冲击脉冲峰值和脉宽可调。运用多体动力学分析软件ADAMS 对经参数优化后的冲击加载机构与试件的冲击过程进行仿真计算,以找到控制冲击脉冲的方法。如图4所示,以凸轮滚子机构的主要零件建立模型,包括凸轮、凸轮轴、滚子、顶杆、力脉冲发生器、试件。分析中作如下假设,试件为刚体且全约束,滚子与凸轮间无摩擦,非线性作用力指数2.2,冲头与试件间无瞬时穿透量,力脉冲发生器中弹性体预压力500 N.
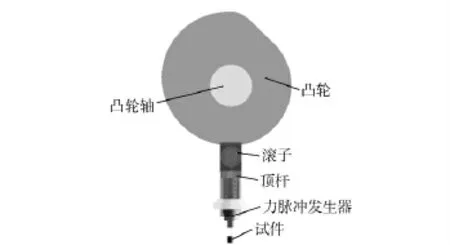
图4 凸轮机构Fig.4 Cam mechanism
本文用冲击脉宽、冲击脉冲峰值、冲击冲量描述冲击脉冲,以冲头与试件发生冲击时的接触刚度kc、力脉冲发生器中弹性体的刚度ke、冲击质量、冲击速度为调节变量。
2.1 kc 对冲击脉冲的影响
更换冲头的材料可实现对kc的调节。图5和表1在力脉冲发生器中的弹性体刚度5 kN/mm,冲头质量10 kg,凸轮轴转速1 000 r/min 时,改变kc得到。其中kc分别为2、5、8 kN/mm 和100 kN/mm.在冲击质量和冲击速度等其他条件不变时,随着kc的增大,冲击脉冲宽度反比减小,脉冲峰值正比增大,而冲击冲量反比于kc.由此可知,改变kc可以调节冲击脉冲的宽度,并获得与自动机膛压曲线上升段相当的冲击载荷及冲击冲量。
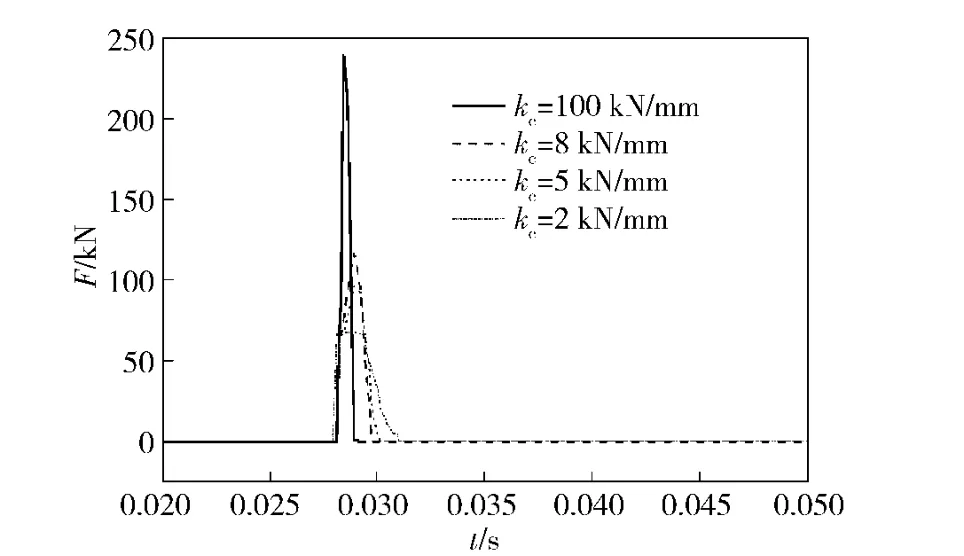
图5 kc 对冲击脉冲的影响Fig.5 Effects of kc on impact pulse
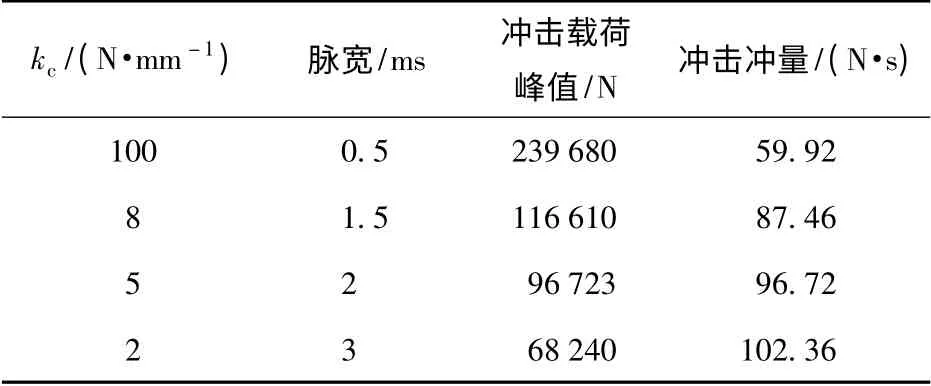
表1 kc 对冲击脉冲影响Tab.1 Effect of kc on impact pulse
2.2 冲击质量和冲击速度对冲击脉冲的影响
冲击冲量正比于冲击质量和冲击速度,改变冲击质量和冲击速度均能够改变冲击冲量。更换冲击头可改变冲击质量,改变凸轮轴转速可改变冲击速度。
通过计算得到如图6所示,不同冲击质量下的冲击脉冲曲线图。其中凸轮轴转速1 000 r/min,kc=100 kN/mm,ke=5 kN/mm,曲线在冲头质量分别为1、3、5、8、10 kg 时得到。由图可知,冲击脉冲峰值正比于冲头质量,冲击脉宽与冲击质量无关,脉冲作用面积即冲击冲量明显增加。冲击质量对冲量的调节作用显而易见,增大冲击质量能够增大冲击冲量。
冲击速度也正比于冲击冲量,加载机构的冲击速度由凸轮轴转速控制。当冲击频率根据要求确定时,冲击速度也随之确定。但因冲击是能量载荷,可通过改变冲击质量满足冲击冲量的要求。
表2为不同转速和kc值条件下,对应的冲击脉冲及冲击冲量,此时冲击质量为10 kg.分析表中数据可知,冲击速度确定时,kc只能在一定范围内对冲击脉宽进行调节。凸轮转速越低,kc对冲击脉宽的调节范围越大。凸轮转速从600~1 000 r/min,kc从2~100 kN/mm,脉宽调节幅度从4.2~2.5 ms.冲击所获得的冲量正比于冲击速度,反比于接触刚度kc.
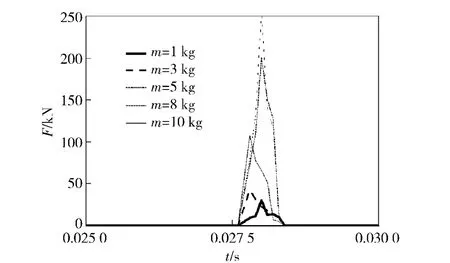
图6 冲击质量对冲量的影响Fig.6 Effect of impact mass on impulse
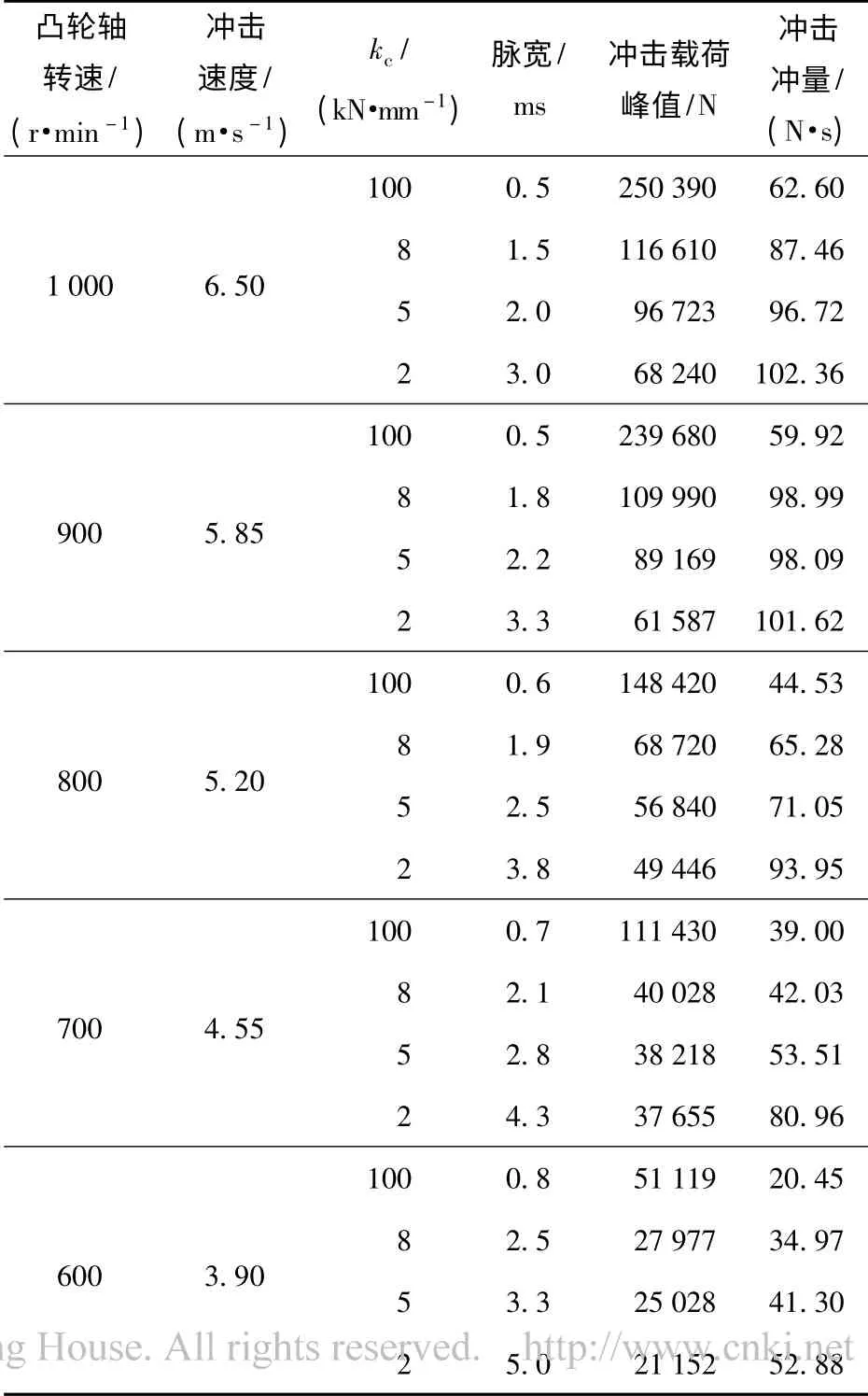
表2 不同冲击速度下kc 对脉冲的影响Tab.2 Effect of kc on pulse at different impact velocities
2.3 ke 对冲击脉冲的影响
根据赫兹理论,冲击脉冲峰值正比于冲击刚度。因此,改变力脉冲发生器中弹性体刚度ke的值,可改变冲击脉冲峰值。图7是在kc分别为2、5、8、100 kN/mm,ke取不同值时得到的冲击脉冲曲线图。此时冲击质量10 kg,凸轮轴转速1 000 r/min。
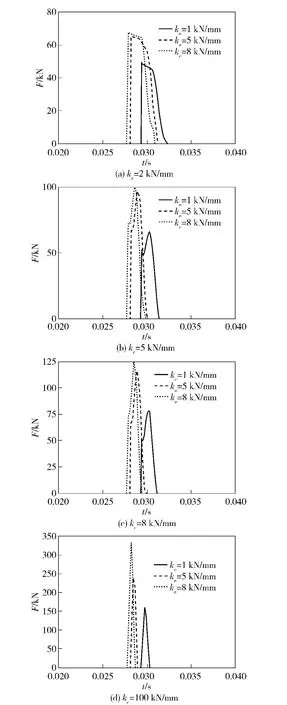
图7 ke 对冲击脉冲的影响Fig.7 Effects of ke on impact pulse
由图可知,冲击脉宽与ke无关,但其对冲击脉冲峰值有较大影响,且正比于脉冲峰值。ke对脉冲峰值的调节能力是有限的,当ke大于5 kN/mm 时,脉冲峰值增幅减小。图中ke增大时,冲击脉冲向时间轴左侧移动。这是由于ke越大,力脉冲发生器中弹性体的变形量越小,冲击脉冲开始作用的时间也就越早。同时,由图可知冲击所获得的冲击冲量正比于ke.由此可知,ke对冲击脉宽无影响,正比于冲击脉冲峰值和冲击冲量。
2.4 冲击脉冲的调节
分析比较以上各图、表中数据可知,4 个调节变量中kc和冲击速度可调节冲击脉宽,而ke和冲击质量与冲击脉宽无关。比较kc和冲击速度以相同比例变化时冲击脉宽的变化幅值,可得到冲击脉宽对冲击速度的变化更敏感。但当冲击频率一定时,冲击速度也随之确定,此时只能通过改变kc值调节冲击脉宽。所以,试验时用kc调节冲击脉宽。但因为前面提到的冲击速度与kc调节脉宽能力的关系,用kc调节脉宽时要考虑这个因素。
4 个调节变量对冲击脉冲峰值均有影响,且4变量都正比于脉冲峰值。比较4 个变量同比例变化时所得到的冲击脉冲峰值变化幅值,以脉冲峰值变化幅值由大到小排列依次为:冲击质量、冲击速度、kc、ke.由此可知,冲击质量对冲击脉冲峰值的影响最大。所以在试验时,冲击脉宽确定后,用冲击质量调节冲击脉冲峰值。
4 个调节变量中,除kc反比于冲击冲量外,其余3 个变量均正比于冲击冲量。比较4 个变量同比例变化时所得冲击冲量变化幅值得到,冲击质量、冲击速度对冲击冲量的调节能力基本相当,ke对应的冲量变化幅值略小于冲击质量和冲击速度,kc引起冲击冲量反向变化。试验时,如调定相关参数后的冲击脉冲峰值和冲击脉宽不能完全满足相应冲击冲量的要求,可用ke作为辅助调节变量对冲量进行适当调节。
4 个变量对冲击脉冲有着不同的影响,同时4 个变量间还有相互关联。冲击频率确定冲击速度,冲击速度影响着kc对冲击脉宽的调节能力及ke对冲击冲量的调节能力,冲击速度越大kc对脉宽的调节能力越小,对ke也是如此。因冲击质量与冲击脉宽无关,所以冲击质量与kc相对应的冲击脉冲峰值有关,对ke的影响也同样如此。也就是说,冲击质量越大,对应的kc、ke所得到的冲击脉冲峰值越大。
综合以上分析结果,可得结论:冲击速度由冲击频率确定,冲击脉宽由kc调节,冲击脉冲峰值由冲击质量调节,ke可作为冲击冲量的辅助调节变量。
根据自动机工作特性,设计冲击疲劳加载机构性能参数为:冲击频率600~1 000 次/min;冲击脉冲峰值5~200 kN;冲击脉宽0.5~5.0 ms;冲击冲量4~120 N·s.调节冲击脉冲的4 个调节变量的调节范围为:冲击速度3.9~6.5 m/s,冲击质量1~12 kg,冲击接触刚度kc为1~100 kN/mm,冲击刚度ke为0.5~8.0 kN/mm.冲击脉冲与调节变量间主要关系如表3所示(表中数据经取整处理)。表中Fi,max和Fi,min分别为当前频率和冲击速度下对应的冲击脉冲峰值上限和下限,Δtmin、Δtmax分别为当前频率和冲击速度下对应的冲击脉宽下限和上限,FΔtmin、FΔtmax分别为当前频率和冲击速度下对应的冲击冲量下限和上限。
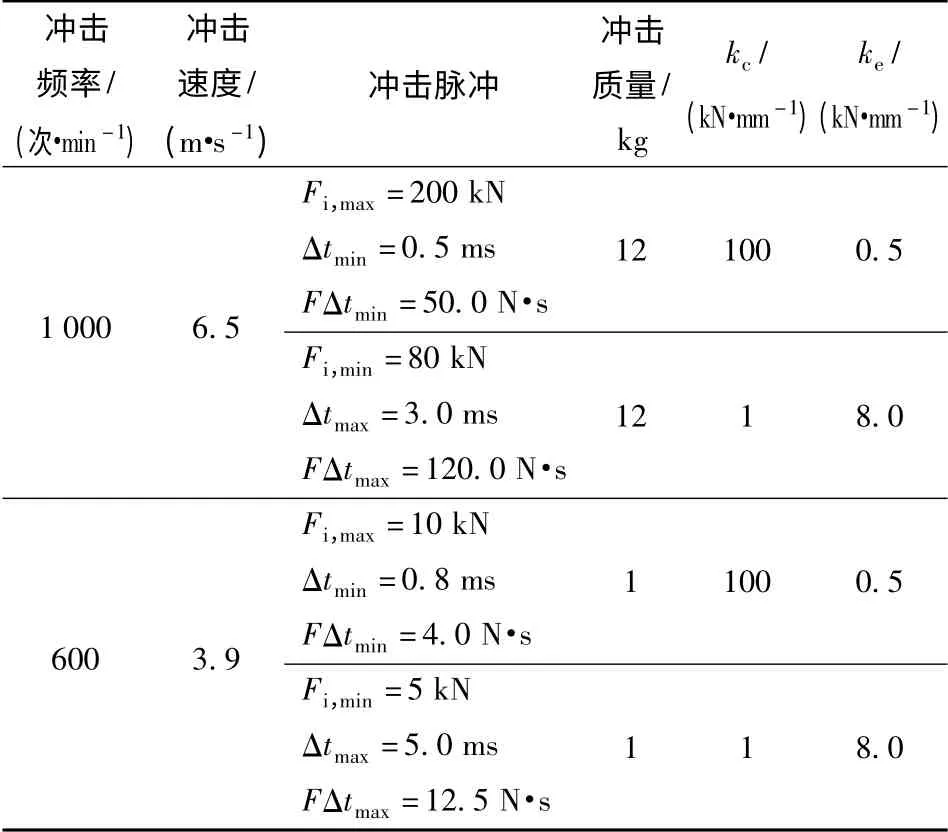
表3 冲击脉冲与调节变量的关系Tab.3 Relation between impact pulse and adjustment variables
3 结论
文中所设计的新型自动机冲击疲劳试验机,可对机头、节套、击锤、击针等枪械自动机关重件直接进行冲击疲劳寿命试验。为解决试验机需要的特殊冲击加载问题,对冲击加载机构进行了设计和优化计算。对优化后的冲击加载机构进行动力学冲击性能分析,计算结果表明冲击加载机构完全能够满足冲击疲劳试验的加载要求。通过调整冲击刚度、冲击质量、速度等参数,可方便地解决冲击疲劳试验加载问题,对冲击脉宽、冲击脉冲峰值及冲击冲量进行调节。文中建立的冲击加载机构的仿真模型,为建立枪械自动机关重件冲击疲劳寿命试验系统提供了理论及技术参考。
References)
[1] 史瑞明.武器撞击动力学[M].北京:兵器工业出版社,1991.SHI Rui-ming,The impact dynamics of weapon[M].Beijing:The Publishing House of Ordnance Industry,1991.(in Chinese)
[2] 王学颜.结构疲劳强度设计与失效分析[M].北京:兵器工业出版社,1991.WANG Xue-yan,The design of mechanism fatigue strength and damage analysis[M].Beijing:The Publishing House of Ordnance Industry,1991.(in Chinese)
[3] 王献超.多冲碰撞试验机研制及其系统动力学响应分析[D].苏州:苏州大学,2007.WANG Xian-chao.Development of repeated impact testing machine and dynamics response analysis of the system[D].Suzhou:Suzhou University,2007.(in Chinese)
[4] 胡志刚.考虑自动机移动的两类机枪动力学模型研究[J].兵工学报,2007,28(11):1293-1297.HU Zhi-gang.Research on two kinds of dynamic models of machine gun system considering moving action mass in receiver[J].Acta Armamentarii,2007,28(11):1293-1297.(in Chinese)
[5] 贾九红,华宏星.新型阻尼器的力学建模与试验[J].机械工程学报,2008,44(8):253-256.JIA Jiu-hong,HUA Hong-xing.Mechanical model and experimental research of a new damper[J].Journal of Mechanical Engineering,2008,44(8):253-256.(in Chinese)
[6] 廖海平,刘启跃,陈兴,等.基于MATLAB 直动滚子凸轮接触应力计算[J].机构设计,2008,25(6):49-51.LIAO Hai-ping,LIU Qi-yue,CHEN Xing,et al.Contact stress calculation of translating roller cam based on MATLAB[J].Mechanism Design,2008,25(6):49-51.(in Chinese)

