水下航行器凸轮发动机凸轮机构的接触应力分析

徐勤超，王树宗，练永庆

(海军工程大学海军兵器新技术应用研究所，湖北 武汉 430033)

水下航行器凸轮发动机凸轮机构的接触应力分析

徐勤超，王树宗，练永庆

(海军工程大学海军兵器新技术应用研究所，湖北 武汉 430033)

水下航行器凸轮发动机的凸轮机构是其主要受力部件，在设计过程中必须进行强度校核。通过对凸轮和圆柱滚轮的接触情况进行分析，运用微分几何理论导出了凸轮的工作曲面方程和接触点的诱导法曲率模型，采用弹性力学中的赫兹理论，建立了凸轮机构的接触应力模型，并进行了算例分析。仿真模型能准确地计算水下航行器凸轮发动机凸轮机构的接触应力，可为其设计和参数的选择提供理论依据。

水下航行器;凸轮发动机;凸轮机构;接触应力

0 引言

水下航行器凸轮发动机的凸轮机构由凸轮和活塞组成。凸轮具有2个向前突起的峰和向后凹陷的谷，活塞后部有2个相隔一定距离的大小圆柱滚轮，它们分别抵着凸轮的前后曲面，把活塞与凸轮联接起来，使活塞的往复运动同凸轮的转动产生关联［1］，具体结构如图1所示。发动机工作时，凸轮和滚轮相接触，气体力和活塞的往复惯性力的合力作用在凸轮上，当合力超过一定限度，凸轮就会发生疲劳破坏，因此必须对凸轮机构的接触强度进行校核。本文通过对凸轮机构的接触情况进行分析，导出了凸轮的工作曲面方程和接触点的诱导法曲率模型，建立了凸轮机构的接触应力的计算模型，并进行了算例分析，本文所建立的模型可为凸轮机构的设计和参数的选择提供理论依据。

1 凸轮工作曲面方程

1.1 坐标系的建立

为方便分析，假定凸轮发动机内轴静止，外轴以相对内轴角速度旋转，选取坐标系O－XYZ为静坐标系，与凸轮固连，原点O为活塞的前止点;X轴与凸轮中心线重合;Y轴位于峰截面(通过凸轮中心线及峰顶的平面)内;Z轴位于谷截面(通过凸轮中心线及谷底的平面)内。O1－X1Y1Z1为动坐标系，与活塞部件前滚轮轴固连，并且绕OX轴旋转，其中X1轴与凸轮中心线重合。Y1轴与活塞部件前滚轮轴线相重合。Y1轴与Y轴之间的夹角为θ，当时间t为0时，2个参考系完全重合。所建立的坐标系如图2所示。

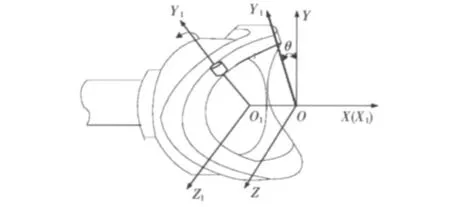
图2 凸轮机构坐标系Fig.2 The reference frame of cam mechanism

1.2 凸轮工作曲面方程

根据凸轮发动机的工作过程，由图3可知，活塞前滚轮与凸轮前工作曲面之间任一接触点P在坐标系O1－X1Y1Z1中的矢量为:

其中，前滚轮与凸轮前工作曲面的接触角为:

根据坐标变换公式可以推导接触点P在坐标系O－XYZ中的矢量为:

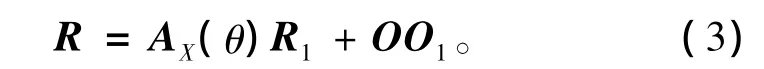
式中:OO1由活塞的运动规律决定，假设凸轮曲线使活塞的位移按其转角的正弦平方规律变化［1］，即OO1=［－H·sin2θ，0，0］T;AX(θ)为坐标变换矩阵。由图2中坐标的位置关系可知:

图3 前滚轮与凸轮前工作曲面的接触角Fig.3 The contact angle between front roller and front working curved surface

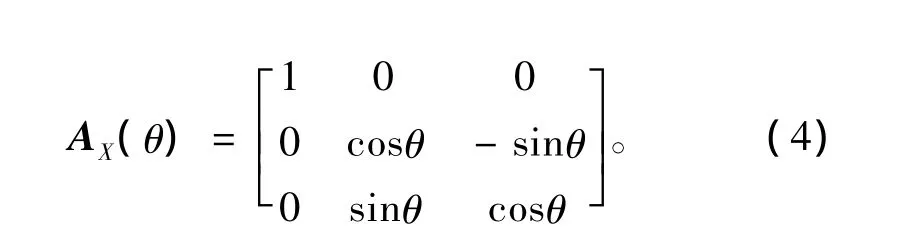
由于坐标系与凸轮固连，可得到凸轮前工作曲面方程为:

为方便求导，凸轮的前工作曲面可表示为关于θ和Rs的函数:

当θ取某一定值时，式(6)表示凸轮前工作曲面与前滚轮的接触线方程，称为Rs线;当Rs取某一定值时，式(6)表示凸轮前工作曲面上的1条曲线，称为θ线。由于凸轮前工作曲面上的受力比后工作曲面上的受力大得多，所以凸轮的后工作曲面一般不进行强度校核。本文只对凸轮前工作曲面的接触应力进行分析，凸轮后工作曲面接触应力的计算同前工作曲面的接触应力计算类似。

2 接触点曲率模型

根据凸轮发动机的工作过程可知，凸轮工作曲面是由滚轮的圆柱表面在一系列位置时所形成的一族圆柱面的包络面［2］，所以凸轮与滚轮接触点的法平面共面。凸轮与滚轮在任一接触点P的几何关系如图4所示。

图4 凸轮和滚轮的接触关系图Fig.4 The contact condition between cam and roller

图中，S为凸轮工作曲面，凸轮与滚轮接触点为P，平面Z为凸轮在接触点P的法平面，同时也是滚轮曲面的法平面，平面Z始终垂直于滚轮的轴线，X为θ线在接触点P处的密切面，n为凸轮曲面在接触点P处的法线矢量，β为θ线在接触点P处的主法线矢量，n和β的夹角为ψ。

由空间曲线的曲率计算公式［3］可得θ线在P点的曲率矢量为:

式中:Rθ为θ线上各点的矢量;且

凸轮前工作曲面接触点法曲率为:

3 接触应力模型

在不考虑活塞与缸体之间摩擦的条件下，按其转角的正弦平方规律变化的单个活塞轴向合力为［1］:

式中:d为气缸直径;n0为内外轴相对转速，r/min;P(θ)为缸内工作气体的压力;Pq为凸轮箱中的压力;mh为单个活塞的质量。当活塞轴向力为正时，大滚轮同前凸轮前工作曲面处于工作状态;当活塞轴向力为负时，小滚轮同后凸轮后工作曲面处于工作状态。

凸轮前工作曲面与前滚轮的法向接触力为:

根据赫兹接触理论可得凸轮前工作曲面所承受的接触应力为:

其中，凸轮前工作曲面与前滚轮的接触线长度lj可由式(5)根据弧长积分公式计算求出。

式中:μ1和μ2分别为凸轮与滚轮材料的泊松比;E1和E2分别为凸轮与滚轮材料的弹性模量;Kng为凸轮与前滚轮的诱导法曲率［4］，Kng=Kn－1/rg。

4 仿真算例及分析

取前滚轮半径rg为10 mm;前滚轮高度h为10 mm;平均压力半径R—s为45 mm;活塞冲程H为20 mm，气缸直径d为20 mm;活塞质量mh为0.2 kg;凸轮箱中的压力pq为1 MPa;凸轮与圆柱滚轮材料的泊松比μ1和μ2均为0.3;凸轮与滚轮材料的弹性模量E1和E2均为200 000 MPa，结合缸内工作气体压力曲线(如图5)进行仿真。由于凸轮前工作曲面和前滚轮的接触载荷和诱导法曲率沿接触线变化连续，取平均压力半径来计算法向接触力和诱导法曲率。通过计算仿真得到活塞的轴向合力、凸轮机构的诱导法曲率、接触线长度如图6～图9所示，将计算结果代入式(12)得到凸轮机构的前工作曲面接触应力如图10所示。

图5 气缸压力随转角变化曲线Fig.5 The curve of pressure with rotational angle of cam

由图6可知，当发动机启动时，转速较低，可近似认为为0，活塞轴向合力在θ为0°时(以下均取θ在0～π之间进行讨论)取得最大值5 340.7 N;当内外轴相对转速n0为4 000 r/min时，活塞轴向合力在θ为38°时取得最大值4 754.8 N。

由图7可知，压力半径Rs分别取40、45和50 mm时，凸轮的前工作曲面和前滚轮的诱导法曲率始终小于0，因此发动机凸轮前工作曲面和前滚轮之间不存在曲率干涉。当凸轮转角θ从0°运动到90°时，诱导法曲率绝对值逐渐减小，且Rs越小，诱导法曲率绝对值降低速度越快。

由图8和图9可知，凸轮前工作曲面与前滚轮的接触线长度在θ为0°和90°时最短，为滚轮高度，但是接触线长度变化不大。当滚轮高度h取10 mm时，接触线长度最大值和最小值之比小于1.003 5;当滚轮高度h取20 mm时，接触线长度最大值和最小值之比为1.014，所以在计算凸轮和滚轮的接触应力时，接触线长度可取滚轮高度进行计算。

由图10可知，发动机启动阶段，活塞惯性力较小，近似认为为0，接触应力在凸轮转角为0°时达到最大为315.1 MPa;当内外轴相对转速n0为4 000 r/min时，活塞轴向合力在θ为36.7°时取得最大值294.9 MPa。发动机启动阶段凸轮机构最大应力值大于其稳定阶段最大应力值。

5 结语

1)从仿真结果可以看出，水下航行器凸轮发动机凸轮机构接触线长度随凸轮转角变化改变不大，在计算凸轮和滚轮的接触应力时，接触线长度可取滚轮高度近似计算。

2)水下航行器凸轮发动机凸轮机构的最大接触应力发生在发动机启动阶段的凸轮峰顶处，对凸轮机构的强度校核，只需验证在启动阶段凸轮峰顶处的接触应力是否超过许用值即可。

3)文中凸轮机构的诱导法曲率的计算模型能用于检验凸轮机构是否存在曲率干涉。

［1］马士杰，等.鱼雷热动力装置设计原理［M］.北京:兵器工业出版社，1992.

MA Shi-jie，et al.Design principle for torpedo thermal equipment［M］.Beijing:Armament Industry Press，1992.

［2］赵寅生.凸轮发动机凸轮和滚轮接触点的曲率计算［J］.水中兵器，1990，(2):37 －45.

ZHAO Yin-sheng.Curvature calculation between cam and roller of cam engine［J］.Underwater Weapon，1990，(2):37－45.

［3］陈维恒.微分几何［M］.北京:北京大学出版社，2006.36－39.

CHEN Wei-heng.Differential geometry［M］.Beijing:Peking University Press，2006.36 －39.

［4］吴序堂.齿轮啮合原理［M］.西安:西安交通大学出版社，2009.197 －210.

WU Xu-tang.Gear meshing principle［M］.Xi'an:Xi'an Jiaotong University Press，2009.197 －210.

［5］曹巨江，陈雪峰.弧面凸轮诱导主曲率与接触应力［J］.机械设计，2001，(11):10 －11.

CAO Ju-jiang，CHEN Xue-feng.The induced main curvature and contact stress of arc surface cam［J］.Mechanical Design，2001，(11):10 －11.

［6］查志武，等.鱼雷热动力技术［M］.北京:国防工业出版社，2006.164 －167.

ZHA Zhi-wu.Technique of torpedo thermal power［M］.Beijing:National Defense Industry Press，2006.164 －167.

Analysis of cam mechanism contact stress for underwater vehicle cam engine

XU Qin-chao，WANG Shu-zong，LIAN Yong-qing
(Naval Research Institute of New Weaponry Technology and Application，Naval University of Engineering，Wuhan 430033，China)

Cam mechanism is one of the most important parts for underwater vehicle cam engine，it must be stress checkout in process of designment.Based on analyzing the meshing condition，the working curved surface equation of cam and the induced normal curvature are modeled by using differential geometric theory，the contact stress models of cam mechanism are modeled based on Hertz theory in elastic mechanics，and the calculating example is made.The simulation models can be used for calculating cam mechanism contact stress correctly，and these models can applied theoretical bases for designing and parameters choosing for cam mechanism.

underwater vehicle;cam engine;cam mechanism;contact stress

TJ630.2

A

1672－7649(2012)03－0040－05

10.3404/j.issn.1672－7649.2012.03.008

2011－07－18;

2011－08－11

徐勤超(1982－)，男，博士研究生，工程师，主要研究方向为鱼雷动力与水下发射技术。