高速供弹机构运动可靠性仿真研究
程刚,张相炎,董志强,董敬芳
(1.南京理工大学 机械工程学院,江苏 南京210094;2.国营第152 厂,重庆400023)
转管自动炮的高速供弹机构通过构件相互冲击、碰撞完成各种规定供弹运动,由于实际生产加工中,供弹机的构件不可避免存在随机定位误差,引起卡滞、停射等故障,可靠性问题比较突出,在供弹机构存在随机定位误差的情况下,如何分析高速供弹机构的运动可靠性一直是自行高炮的难题,文献[1]建立四杆驱动机构动力学的数学模型,分析杆结构的受载变形、制造误差等因素对运动可靠性的影响。本文提出了基于多体动力学的运动可靠性仿真分析方法,以转管自动炮的高速供弹机构为研究对象,通过蒙特卡洛随机抽样,模拟拨弹轮的初始定位角的随机误差,结合参数化驱动方法,完成了供弹过程的随机抽样仿真,利用机械可靠性的应力干涉理论,分析了拨弹轮初始定位角误差对拨弹机构供弹可靠性的影响。
1 建立供弹机参数化驱动仿真模型
把转管自动炮高速供弹机构三维实体模型转化为Parasolid 格式并导入机械动力学仿真软件ADAMS 中,建立高速供弹机构的参数化仿真模型,如图1所示。各拨弹轮与供弹机支架通过转动铰链相连,炮弹与拨弹轮和导轨均为接触碰撞,采用关联副连接4 个拨弹轮的铰接副,使4 个拨弹轮等速转动,把炮弹从弹箱快速输送至自动炮进弹口。在实际制造装配时,4 个拨弹轮定位角均存在随机误差,只有合理设计初始定位角,使其在随机定位误差存在条件下仍能可靠地供弹,才能降低供弹卡滞、供弹阻力过大等故障的发生概率。
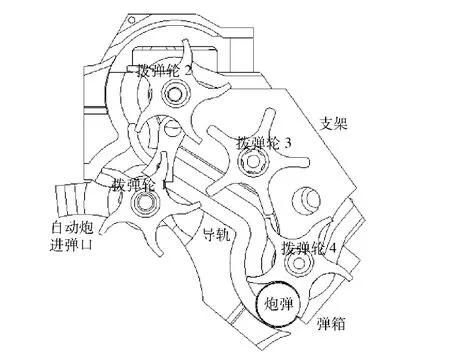
图1 高速供弹机动力学仿真模型Fig.1 Dynamic simulation model of high speed feed mechanism
在ADAMS 动力学仿真模型中,拨弹轮的空间定位均采用连体坐标系,对拨弹轮初始定位角的参数化驱动需通过驱动连体坐标系的转动实现,在仿真模型中,定义第i 个拨弹轮的初始定位角为设计变量DVji,通过驱动设计变量改变拨弹轮的初始定位角。但是,参数化驱动拨弹轮的初始定位角会导致拨弹轮质心的移动,如图2所示,某个拨弹轮的质心位于P 点,rP为点P 在大地坐标系OXYZ 中的坐标矢量,r 为拨弹轮的连体坐标系oxyz 原点o'在大地坐标系OXYZ 中的坐标矢量,sP为拨弹轮的质心在连体坐标系oxyz 中的坐标矢量,当驱动拨弹轮的初始定位角变化时,连体坐标系oxyz 旋转至ox'y'z',拨弹轮的质心P 随连体坐标系转动至P'点,这会导致仿真模型的转动铰链约束关系失效。由图2可知
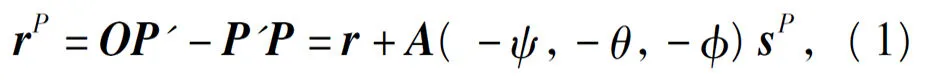
式中:A(ψ,θ,φ)为oxyz 相对于ox'y'z'的方向余弦矩阵,ψ 为进动角,θ 为章动角,φ 为自转角。按照(1)式,令第i 个拨弹轮质心位置为位置变换函数f(DVji),当对拨弹轮初始定位角进行参数化驱动时,位置变换函数可根据设计变量DVji计算出P'P和rP,把拨弹轮的质心从P'移回到P 点,这样,在改变拨弹轮初始定位角的同时,可避免仿真模型中转动铰链约束失效,从而顺利进行参数化驱动仿真。
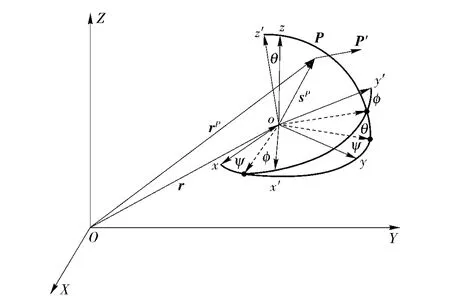
图2 改变拨弹轮初始定位角引起的质心位移Fig.2 Centroid displacement caused by change of setting angle of transmission gears
2 拨弹轮初始定位角误差的随机抽样
由于加工及装配误差的存在,每个拨弹轮的初始定位角均存在误差,且误差符合正态分布,可采用蒙特卡洛法抽样法模拟拨弹轮初始定位角的随机误差[2-3]
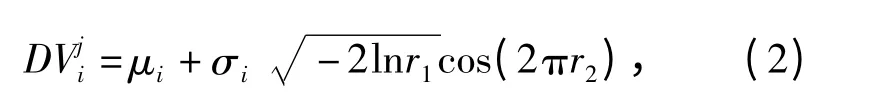
式中:DVji为第i 个拨弹轮初始定位角的随机抽样,该抽样服从正态分布,j 为抽样的样本号;μi、σi分别为第i 个拨弹轮初始定位角的设计值和标准差;r2、r1为[0,1]区间均匀分布随机数,取j=400.
为了比较初始定位角的设计值对供弹运动可靠性的影响,表1列出了2 组初始定位角的随机抽样。第1 组4 个拨弹轮的定位角的设计值:μ1=0.1、μ2=4、μ3=0、μ4=3.5;均方差:σ1=σ2=σ3=σ4=0.167.第2 组4 个拨弹轮的定位角的设计值:μ1=0.2、μ2=4.5、μ3=- 0.2、μ4=3.6;均方差:σ1=σ2=σ3=σ4=0.167.
3 拨弹轮初始定位角的参数化驱动和仿真
编制基于ADAMS 的参数化仿真驱动程序,按照蒙特卡洛抽样的结果对供弹机构实施参数化驱动仿真,每次读取一行随机数抽样作为设计变量(DV1j,DV2j,DV3j,DV4j),通过驱动设计变量来改变4个拨弹轮的初始定位角,并完成对应的供弹动力学仿真。重复该过程,对供弹机构进行400 次供弹动力学仿真,输出炮弹运动速度、位置等结果。对400组输出的仿真结果进行统计分析,可得供弹过程中t时刻炮弹位置的均值
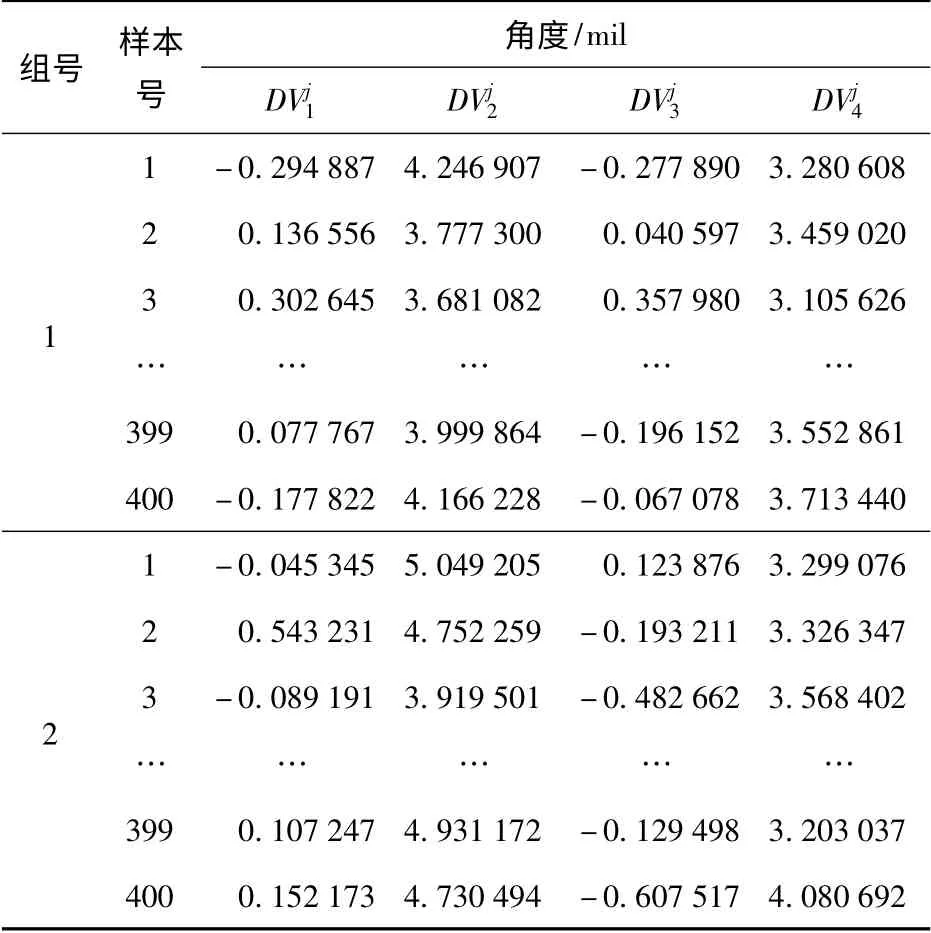
表1 4 个拨弹轮初始定位角的随机抽样表Tab.1 Sample groups of four transmission gears’setting angle

t 时刻炮弹位置的均方差
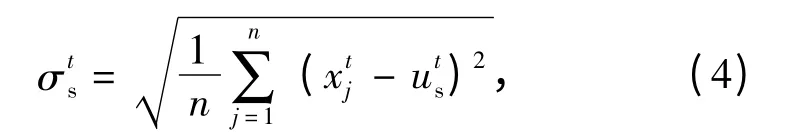
式中:n=400,2 组抽样得到的仿真结果如图3和图4所示。图3为炮弹运动过程中的位置均值,纵坐标为炮弹质心在t 时刻的位置均值sts,计算该位移均值的样本是ADAMS 仿真输出的位置幅值xtj=图4为仿真得出的炮弹运动过程中的速度均值曲线,纵坐标为炮弹质心运动速度。
由图3和图4可以看出,2 组抽样参数仿真得到的炮弹运动速度和位置的波动均不大,难以对比初始定位角的设计值μi的优劣。这里,利用应力干涉理论,以炮弹运动到位情况作为运动可靠度评价指标,建立供弹过程中的运动可靠性计算模型,比较初始定位角的设计值μi对运动可靠度的影响。
4 运动可靠性分析计算
转管自动炮是在转动过程中完成连续射击运动循环的,最理想的供弹过程为匀速供弹,拨弹机构受到的冲击力最小,运动可靠性最高。因此,炮弹在t时刻的期望位置为
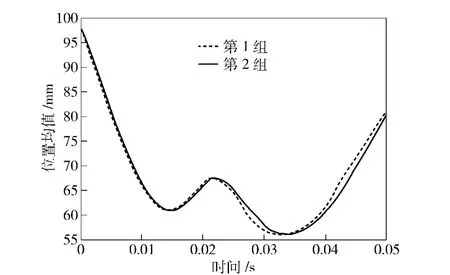
图3 2 组抽样得到的炮弹运动轨迹的均值Fig.3 Projectile’s average motion trace obtained from two sample groups
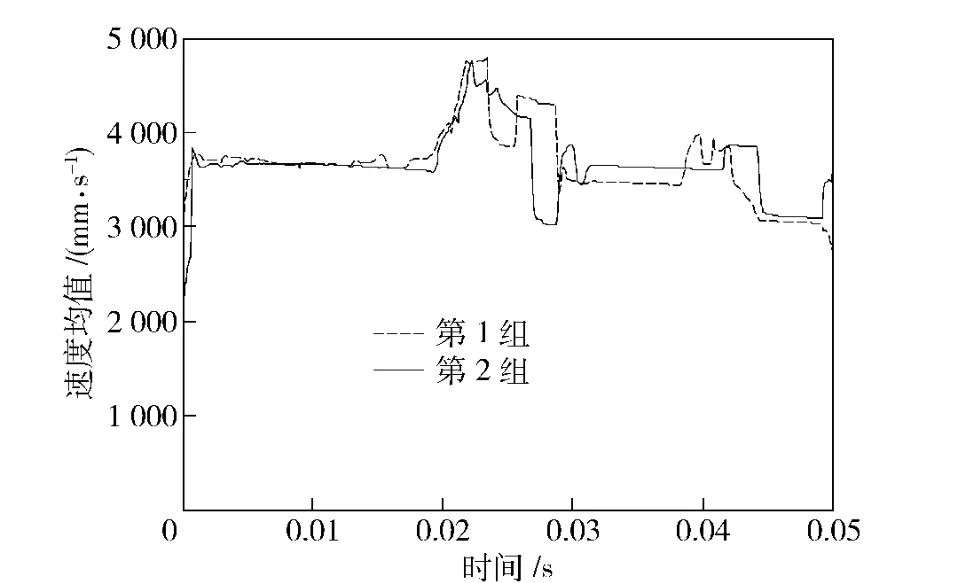
图4 2 组抽样得到的炮弹速度均值Fig.4 Projectile's average motion speed obtainedfrom two sample groups

式中:vo为期望的炮弹恒定移动速度。在供弹过程中,拨弹轮的定位角误差由制造误差和驱动参数误差构成,由于拨弹轮采用同一套驱动装置完成转动驱动,驱动装置的误差对4 个拨弹轮的影响是相同的,可看作系统误差,因此,只考虑制造误差对供弹运动可靠性的影响。拨弹轮定位角的制造误差由驱动拨弹轮转动的各构件设计公差确定,根据各构件的传动比、传动角度等关系,把各执行机构设计公差的均方差折算到拨弹轮转轴上,即可得到各构件对拨弹轮转轴的影响值Δσj.按照供弹机构尺寸链关系,即可得到拨弹轮驱动炮弹位置的均方差
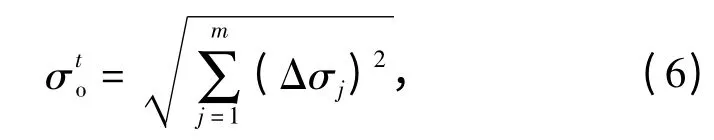
式中m 为影响拨弹轮转动误差的构件数量。
利用应力—强度干涉模型计算供弹的运动可靠性,如图5所示,图中,横坐标为t 时刻炮弹可能的位置,纵坐标为位置的概率,在t 时刻,炮弹的理想位置为uto,均方差为σto,其误差分布符合正态分布,分布函数为f(u),容许的上下限误差区间为],sts为动力学仿真得到的t 时刻炮弹位置的均值,均方差为σts,其误差分布符合正态分布,分布函数为f(s).
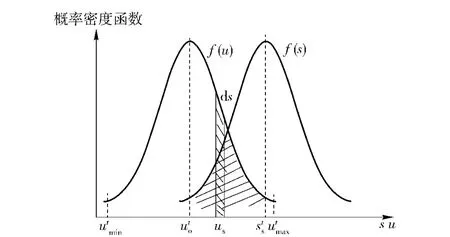
图5 运动可靠性应力—强度干涉模型Fig.5 Stress-strength interference model of motion reliability

t 时刻炮弹运动位置处于ds 区间的概率为
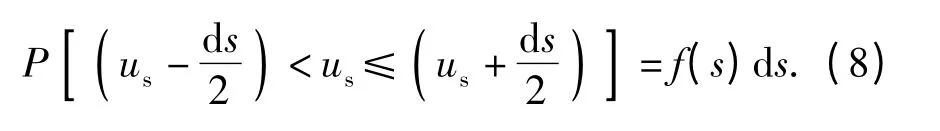
由于(7)式和(8)式是2 个独立的随机事件,2者同时发生的概率即为供弹的运动可靠度
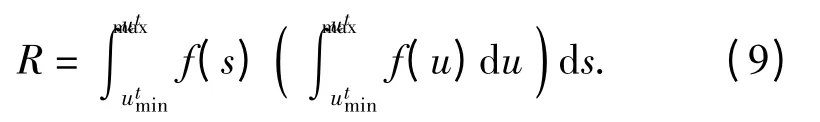
对(9)式进行离散化求解,可得到拨弹过程中各时刻的运动可靠度,表1中2 组输入参数的运动可靠性计算结果如图6所示。
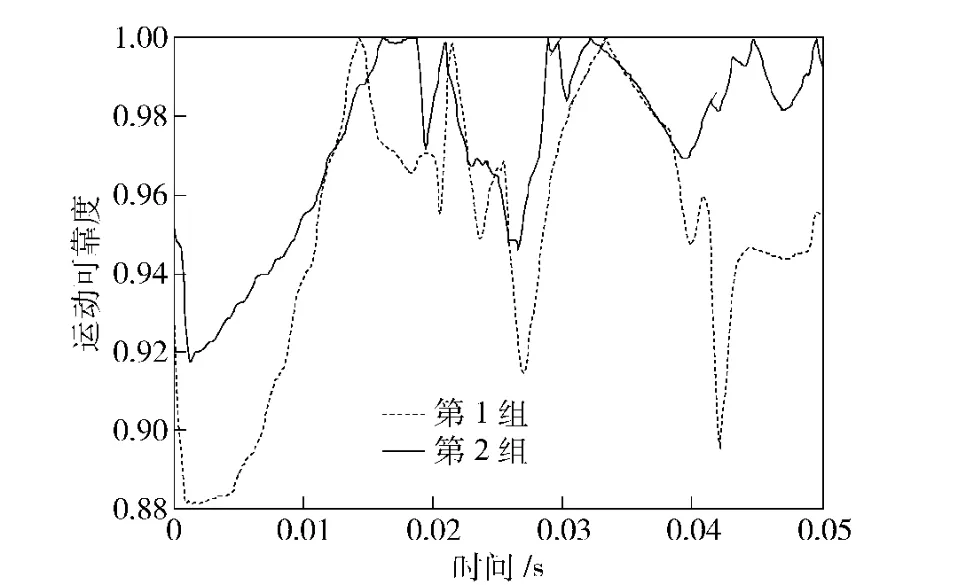
图6 2 组抽样得到的供弹运动可靠度Fig.6 Feeding motion reliability obtained from two sample groups
图6中,第1 组供弹过程的平均可靠度为0.950 8,第2 组供弹过程的平均可靠度为0.973 3,可见,尽管2 组抽样得到的炮弹的运动轨迹比较接近,但是,第1 组参数的供弹可靠性低于第2 组,这是因为第1 组参数对随机定位误差的“忍受”能力弱于第2 组参数,当随机定位误差较大时,炮弹位置更容易超出容许的上下限误差发生卡弹的概率高于第2 组参数,因此,运动可靠性比较低。
通过对供弹机的2 组参数进行运动可靠性仿真分析和比较,确定了某供弹机各拨弹轮优化后的定位角设计值μi,根据3σ 原则,各拨弹轮的初始定位角在[μi+3σi,μi-3σi]区间内,供弹机能够更可靠地供弹。可靠性射击试验的结果表明,和第1 组相比,采用第2 组初始定位角的供弹机,连续供弹过程平稳,平均无故障供弹时间从2 800 发提高到3 200发,证明了运动可靠性仿真的可信性。
5 结论
结合可靠性的应力干涉理论,提出了供弹机构的运动可靠性仿真方法,在供弹机的拨弹轮存在定位误差时,分析和比较结构设计参数对供弹机构运动可靠性的影响,并通过试验验证了运动可靠性仿真方法的正确性提高了供弹机构的运动可靠性,为此类机构的运动可靠性评估提供了可行的方法。
References)
[1] 纪玉杰,孙志礼,李良巧.曲柄滑块机构运动可靠性的仿真[J].兵工学报,2006,27(1):116-120.JI Yun-jie,SUN Zhi-li,LI Liang-qiao.Simulation on motion reliability of crank-slider mechanism[J].Acta Armamentarii,2006,27(1):116-120.(in Chinese)
[2] 孙志礼,陈良玉.实用机械可靠性设计理论与方法[M].北京:科学出版社,2003:221-237.SUN Zhi-li,CHEN Liang-yu.Applied mechanical reliability design theory and method[M].Beijing:Science Press,2003:221-237.(in Chinese)
[3] Mainak Mazumdar,David W Coit,Kevin McBride.A highly efficient Monte Carlo method for assessment of system reliability based on a Markov model[J].American Journal of Mathematical and Management Sciences,1999,19(1):115-133.
[4] 张义民,黄贤振,贺向东.不完全概率信息牛头刨床机构运动精度可靠性稳健设计[J].机械工程学报,2009,45(4):105-110.ZHANG Yi-min,HUANG Xian-zhen,HE Xiang-dong.Reliability-based robust design for kinematic accuracy of the shaper mechanism under in-complete probability information[J].Journal of Mechanical Engineering,2009,45(4):105-110.(in Chinese)
[5] 杨强,孙志礼,闫明,等.改进Delta 并联机构运动可靠性分析[J].航空学报,2008,29(2):487-491.YANG Qiang,SUN Zhi-li,YAN Ming,et al.Kinematic reliability of improved Delta parallel mechanism[J].Acta Aeronautica Et Astronautica Sinica,2008,29(2):487-491.(in Chinese)

