基于Gibbs抽样的马尔科夫蒙特卡罗方法在结构物理参数识别及损伤定位中的研究

刘书奎，吴子燕，张玉兵

（西北工业大学 力学与土木建筑学院，西安 710072）

近些年来结构物理参数的识别引起了人们的广泛关注［1－4］。但由于结构材料的不均匀性，施工质量的易变性，作用荷载的随机性等不确定性因素的影响，观测数据和结构模型均具有强烈的本质不确定性，从而导致结构物理参数识别问题成为不确定性问题［5］。因此，必须在确定性物理参数识别研究的基础上，发展能够合理反映不确定性特性的物理参数识别概率方法。

贝叶斯方法能够综合先验和条件信息，并且给出明确的后验信息，因此被广泛地应用于不确定性问题。在土木工程领域，Beck等人［6］首先提出了系统辨识的贝叶斯统计模型，但这是一种渐渐逼近的方法，要保证其精确性就必须得到足够多的模态数据。为解决该问题，Beck和 Au等人［7］又提出了基于 Metropolis-Hastings抽样的马尔科夫蒙特卡罗方法，该方法的一个局限在于仅对低维问题有效。Ching和Cheng［8］提出了变异的蒙特卡罗马尔科夫方法（TMCMC），避免了直接从后验分布中抽样，但构造的马尔科夫链的“burn-in”阶段非常长，基于Gibbs抽样的马尔科夫蒙特卡罗方法可以很好的解决高维参数识别问题［9］。文献［5］中利用了Gibbs抽样来进行物理参数概率识别，但所利用的初始条件是确定性的结构模态参数。由于环境影响、测试误差以及分析过程中的简化，引入了不确定因素，造成实测模态参数与真值之间不可避免地存在偏差［10］。

本文视结构模态参数为随机变量，根据结构动力特征方程，将模态参数与结构物理参数通过线性结构识别模型联系起来，采用基于Gibbs抽样的马尔科夫蒙特卡罗方法来对结构物理参数进行后验抽样，进而根据后验样本的统计特性进行结构物理参数识别及损伤定位。

1 线性回归模型

线性回归模型通常表示如下［11］：

其中，Y∈Rn为观测模型输出，X∈Rn×m为观测回归量矩阵，θ∈Rm为模型参数向量，Xθ为理论模型输出，e∈Rn为预测误差，服从均值为零，协方差矩阵为的n维正态分布。

假设模型参数θ的先验分布为不正常的均匀分布，即为：

预测误差方差的先验分布为倒伽马分布IG（α，β），即为：

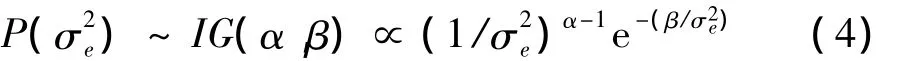
当α=β=0时，该先验分布就转变为通常的无信息先验分布，即：

由贝叶斯估计理论，模型参数θ和预测误差方差的后验联合分布为：

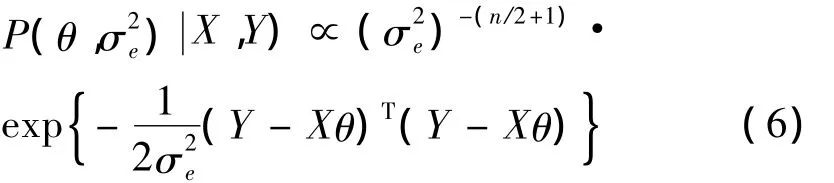
若使用 Gibbs抽样，还需知道θ、的条件后验分布［11］：

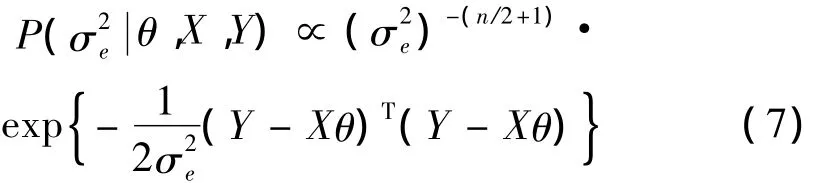
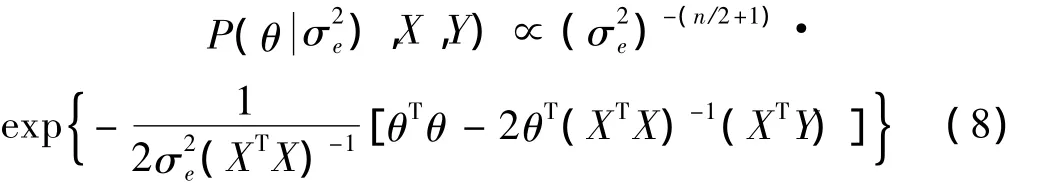
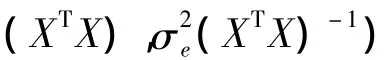
2 线性结构识别模型

在结构健康监测领域，通常用线性结构模型来进行模型更新。一般振动测试数据都是在很低幅值的激励下得到的，因此很多结构包括损伤结构都近似地表现出线性行为［9］。

结构第i阶模态的理论频率和振型向量φi应满足如下特征方程：

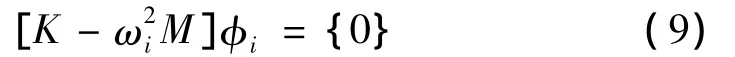
其中φi=［φi1，φi2，…，φim］T，m为结构自由度数目。当采用集中质量矩阵时，该方程可以表示为：

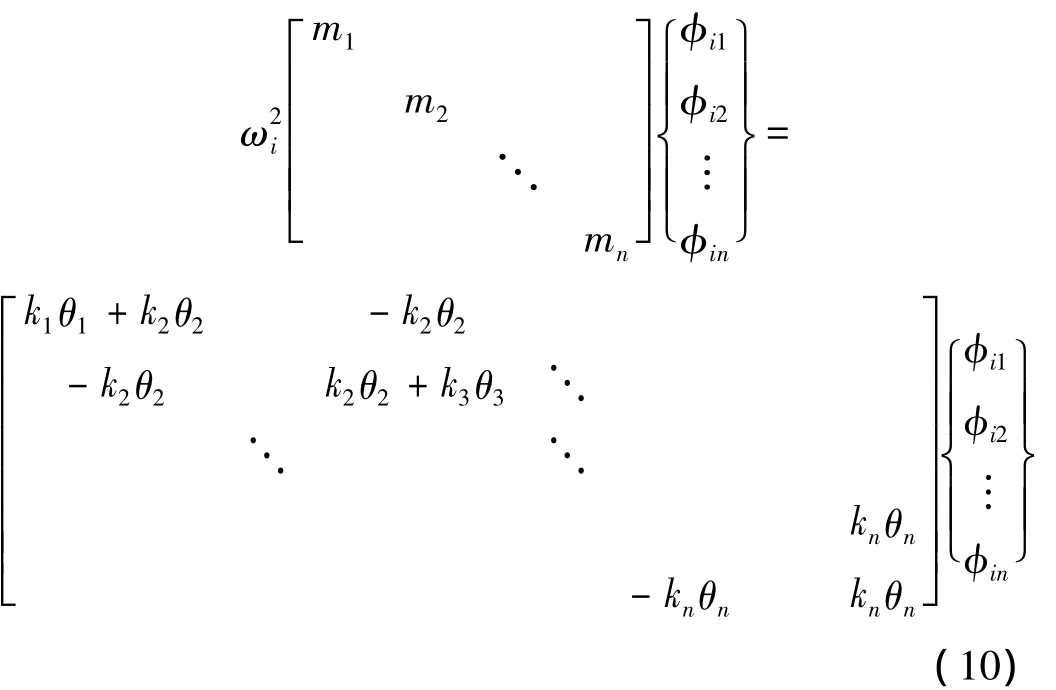
其中，θ1，θ2，…，θn为无量纲的归一化参数（以下称其为结构刚度参数），且恒大于0，表示某一构件对总体刚度矩阵的贡献，当θi小于1时，即可判断该构件发生损伤，由θi大小，可判断损伤的程度。由于结构质量对损伤敏感程度较低，在上述方程中视结构质量为常量，当需要对其进行识别时，运用同样的处理方法对式（10）做适当变换即可。

对式（10）做变换，并加入预测误差项，可得线性结构识别模型：

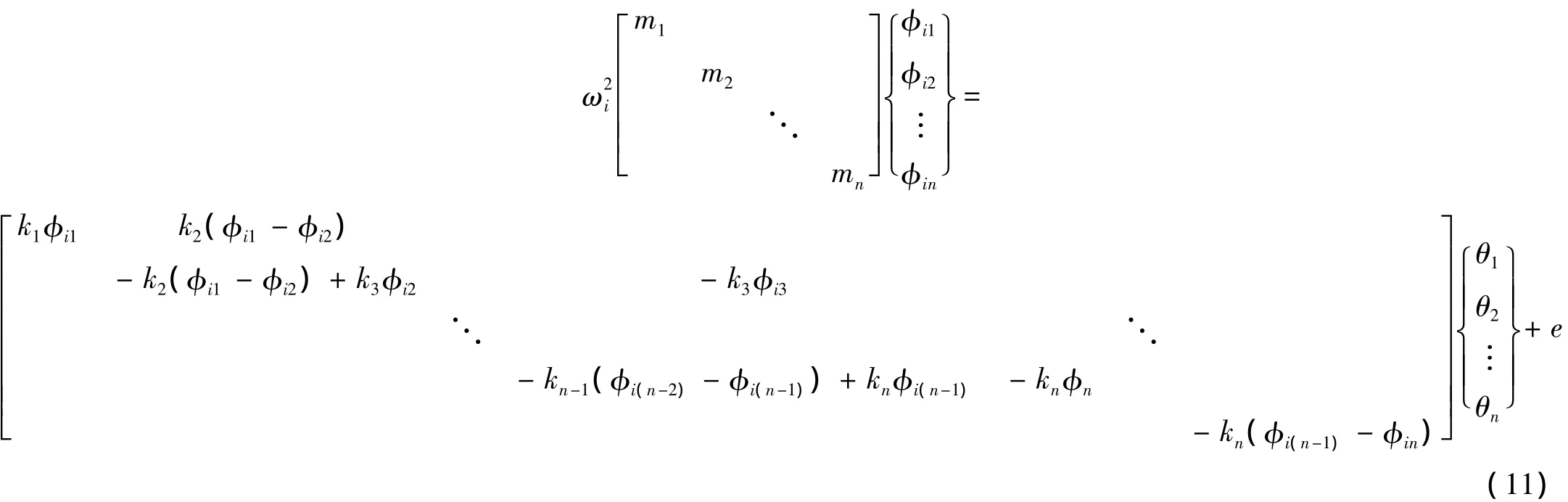
对应于线性回归模型Y=Xθ+e。

3 Gibbs抽样过程

本文通过Matlab编程，按照以下步骤实现Gibbs抽样：

（2）a.根据式（11）并结合的条件后验分布即式（7），抽取

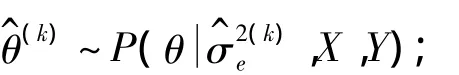
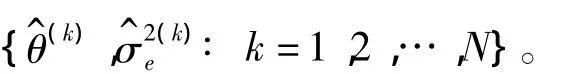
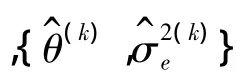
4 损伤概率

刚度参数向量θ中的元素与结构构件存在一一对应关系，本文利用θ中某一元素出现降低来标识损伤的位置，以其降低的比例d来刻画损伤的程度。

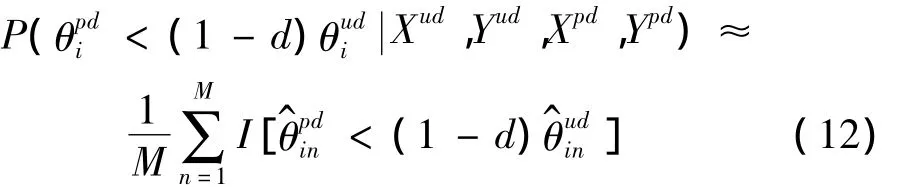
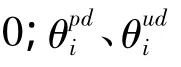
5 算例分析

算例为某三层剪切型结构（图1）。本文模拟了三种损伤类型：类型1（DP1）：结构第一层的刚度降低30%；类型2（DP2）：结构第二层的刚度降低30%，第三层的刚度降低50%；类型3（DP3）：结构第一层刚度降低50%、第二层刚度降低40%、第三层刚度降低30%。在进行Gibbs抽样之前，需要先识别出结构的模态参数（本文中利用的是结构的圆频率），识别结构模态参数的方法有时间序列法、随机减量法、NExT、随机子空间法以及最近由任宜春等提出的基于改进L－P小波的时变模态参数识别方法［12］等。为考虑结构自振圆频率的随机性，本文假设其服从以其理论值为均值的正态分布，其分布规律如表1所示。在Gibbs抽样过程中结构自振圆频率均根据该统计规律随机产生。

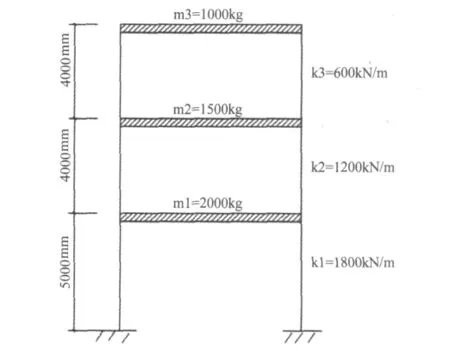
图1 三层剪切型结构Fig.1 Three-story shear-building

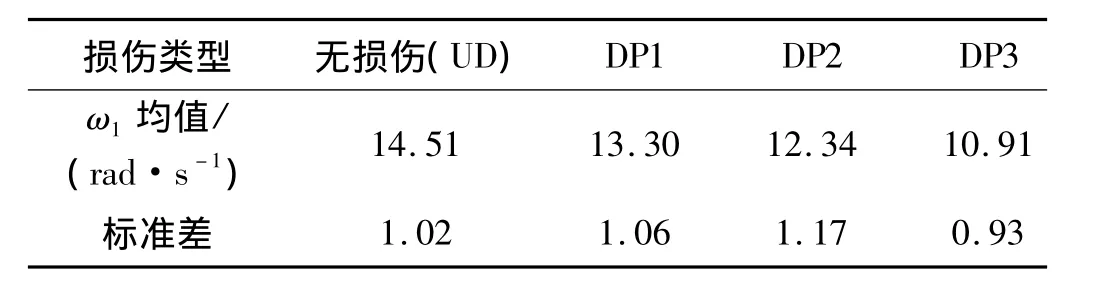
表1 结构一阶自振圆频率统计特性Tab.1 Statistical properties of the first-order natural frequency

方便起见，对以上四种类型，均取刚度参数向量初值θ=［0.8 0.8 0.8］T，θ1、θ3、θ3的 Gibbs抽样曲线如下图所示。

由图2可以看出，不同损伤类型，当结构某处发生刚度降低时，对应的结构刚度参数θi的抽样曲线也会发生明显变化，从而可以清楚地判断出结构的损伤位置及程度。

图3显示的是不同参数空间下的抽样结果，参数之间表现出近似的线性关系，这表明了识别结果的可靠性。图3同样可以判断损伤的位置及程度，如在图3.1中，以“+”号表示的图像（DP1）相比以“o”号表示的图像（UD）在θ1方向上发生了明显的左移，而在θ2方向上并未发生明显的偏移，这说明在DP1下结构的第一层柱子k1发生了刚度降低，而结构的第二层柱子k2并未明显地出现刚度变化。值得注意的是，在图3.3中以“+”号表示的图像（DP1）和“o”号表示的图像（UD）发生了重合，这是由于结构在损伤类型DP1下仅第一层柱设定了刚度降低，第二层和第三层柱未设定损伤，图3.3 是在（θ2，θ3）空间的抽样结果，这又一次验证了识别结果的可靠性。

由式（12），可以得到结构某一层柱子在不同损伤类型下发生不同刚度降低的超越概率（图4），亦即其降低的超过某一比例d的概率，当d取值不同时，超越概率也就不同，这样取一系列d值，最终得到图4。该图除了能够判断结构的损伤位置及程度外，还可以给出结构在某处损伤程度的概率度量，这也正是贝叶斯方法在处理不确定性问题时的优越之处。

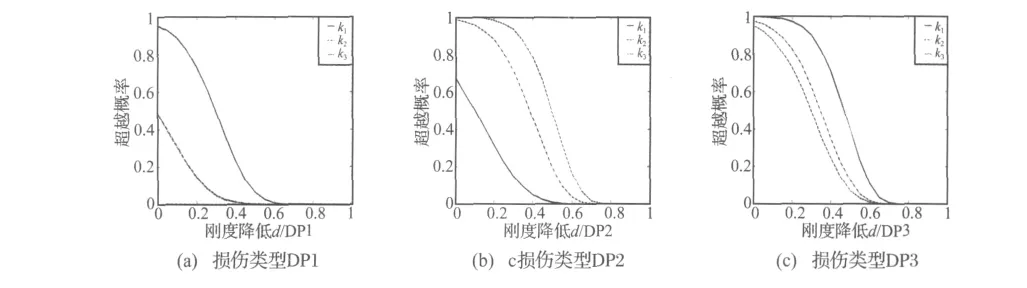
图4 结构在不同损伤类型下对应不同刚度降低的超越概率Fig.4 Estimated damage probability cures for all damaged patterns

表2 结构刚度参数后验样本的统计特性Tab.2 Posterior statistical properties of the stiffness parameters

表2为结构刚度参数后验样本的统计特性。由于在结构响应中加入了噪声，考虑了结构自振圆频率的随机性，且仅采用了结构一阶频率等因素的影响，当损伤位置及程度增加时，识别的误差有所增大，但能满足工程基本要求。

6 结论

本文首先通过对结构的动力特征方程进行一系列的变化，得到线性结构识别模型，进一步由贝叶斯更新理论得到模型中参数的后验分布形式。利用结构的模态参数，并考虑其随机性，应用基于Gibbs抽样的马尔科夫蒙特卡罗方法对线性结构识别模型的条件后验分布进行了抽样，避免了对后验分布的直接抽样，并克服了Metropolis-Hastings抽样仅对低维问题有效的缺陷，成功地实现了结构物理参数识别及损伤定位。数值算例表明：Gibbs抽样结果除了可以以不同的方式标识结构的损伤程度及位置且识别的误差较小外，还能给出识别值的概率度量。

［1］Moaveni B，He X，Conte J P.Damage identification of a composite beam using finite element model updating［J］.Computer-Aided Civil and Infrastructure Engineering，2008（23）：339－359.

［2］张 坤，罗绍湘，段忠东.基于动态响应灵敏度同步反演结构物理参数与输入的算法［J］.振动与冲击，2009，28（9）：143 －148，167.

［3］Muto M M.Application of stochastic simulation methods to system identification［D］.California Institute of Technology，Pasadena，California，2007.

［4］Cheung S H，Beck J L.Bayesian Model Updating Using Hybrid Monte Carlo Simulation with Application to Structural Dynamic Models with Many Uncertain Parameters ［J］.Journal ofEngineering Mechanics， 2009， 135（4）：243－255.

［5］李小华.结构参数识别的贝叶斯方法及应用研究［D］.中国地震局工程力学研究所，2009.

［6］ Beck J L，Katafygiotis L S.Updating models and their uncertaintiesI：Bayesian statistical［J］. Journalof Engineering Mechanics，1998，124（4）：455 －461.

［7］Beck J L，Au S K.Bayesian updating of structural models and reliability using Markov chain Monte Carlo simulation［J］. JournalofEngineering Mechanics，2002，128：380－391.

［8］ Ching J，Chen Y J.Transitional markov chain monte carlo method for bayesian model updating，model class selection，and model averaging［J］.Journal of Engineering Mechanics，2007，133（7）：816 －832.

［9］Ching J，Muto M，Beck J L.Structural model updating and health monitoring with incomplete modal data using Gibbs sampler［J］.Computer － Aided Civil and Infrastructure Engineering，2006，21：242 －257.

［10］易伟建，吴高烈，徐 丽.模态参数不确定性分析的贝叶斯方法研究［J］.计算力学学报，2006，26（6）：700 －705.

［11］ Scott M L.Introduction to applied bayesian statistics and estimation for social scientists［M］.Springer，2007.

［12］任宜春，张杰峰，易伟建.基于改进L-P小波的时变模态参数识别方法［J］.振动与冲击，2009，28（3）：144 －148.