基于自适应多尺度形态梯度变换的滚动轴承故障特征提取

李 兵， 张培林， 刘东升， 米双山， 任国全

（1.石家庄军械工程学院 自行火炮教研室，石家庄 050003；2.石家庄军械工程学院 导弹机电工程教研室，石家庄 050003）

滚动轴承是各种机械设备中最为常用的部件，其运行状态对整台机器的安全运行影响最大。当滚动轴承存在局部缺陷时，其振动信号中的脉冲信号含有丰富的缺陷信息，如果能够有效地将缺陷引起的脉冲信号提取出来，便可以诊断出缺陷存在的部位［1］。

数学形态学是在随机集和积分几何基础上发展起来的一种非线性分析方法，它根据处理对象的形状特征，用特定的结构元素进行形态变换来达到信号处理的目的。该方法进行信号处理时只取决于待处理信号的局部形状特征，通过数学形态变换将一个复杂的信号分解为具有物理意义的各个部分，将其与背景剥离，同时保持信号主要的形状特征，要比传统的线性滤波更为有效［2，3］。数学形态滤波器已经在数字图像处理、计算机视觉和模式识别等领域得到了广泛的应用［4］，同时在电力系统、心电脑电信号处理中也得到充分的利用［5，6］。近年来，数学形态滤波逐渐引入了机械故障诊断领域，文献［7］采样形态闭算子对轴承故障信号进行了分析，并得出了结构元素的最佳尺寸范围，文献［8－10］采用形态闭算子对轴承、齿轮进行了特征提取，文献［11］提出了一种形态非抽样小波对转子振动冲击特征信号提取，取得了一定的效果。

但上述方法均采用单一尺度的结构元素对信号进行处理，小尺度下能够保留更多的信号细节，但同时会受到噪声的影响，大尺度下虽能较大程度的抑制噪声，但信号细节也会被模糊化，因此单尺度形态变换用于提取信号的冲击特征存在着一定的不足。

针对单尺度变换存在的问题，本文提出了一种自适应多尺度形态梯度变换（AMMG），以同时满足保持信号细节和抑制噪声的功能，通过仿真信号和实测轴承故障信号分析，并与形态闭算子和包络解调方法进行对比研究，结果表明自适应多尺度形态梯度变换在强背景噪声下能更有效的提取出信号中的冲击脉冲信号，并且计算简单、快速，可广泛应用于机械故障诊断的在线分析。

1 自适应多尺度形态梯度变换

1.1 数学形态学基本变换

数学形态学变换的基本思想是基于信号的几何结构特征，利用预先定义的结构元素（相当于滤波窗）对信号进行匹配或局部修正，以达到提取信号，抑制噪声的目的。

数学形态学的基本变换包括腐蚀、膨胀两种基本算子，通常包括二值形态变换和灰值形态变换。由于振动信号是一维多值信号，本文只给出一维灰值数学形态学的基本变换。

设f（n）和g（m）分别为定义在F={0，1，2，…，N－1}和G={0，1，2，…，M－1}上的离散函数，且N≫M。这里为f（n）输入信号，g（m）为结构元素。

f（n）关于g（m）的腐蚀定义为：

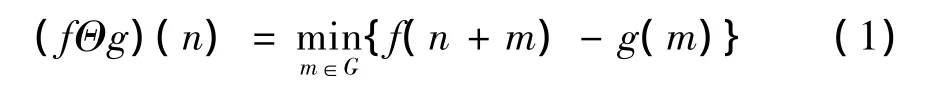
f（n）关于g（m）的膨胀定义为：

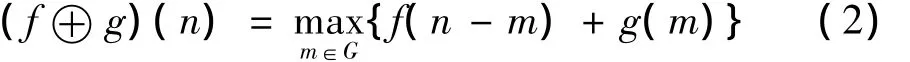
腐蚀和膨胀运算等价于离散函数在滑动滤波窗（相当于结构元素）内的最小值和最大值滤波。在一维信号分析中，腐蚀运算抑制了信号的正脉冲，而保留了信号中的负脉冲；而膨胀运算抑制信号的负脉冲，保留信号的正脉冲。

由式（1）、式（2）可见，腐蚀和膨胀的计算相当简单，只包含加减法运算（取极值运算是由若干个比较运算构成，比较运算实际上就是减法），不涉及乘除，因而在对信号的处理速度方面具有很大的优势。

1.2 形态梯度变换

虽然形态学腐蚀和膨胀都可以提取信号的脉冲信息，但只能分别提取信号中的负脉冲或者正脉冲信息，在实际应用中，有时很难得到实际信号正、负冲击的先验知识，而且更普遍的情况是信号同时具有正、负冲击。这时，需要利用腐蚀、膨胀运算的组合来构建形态梯度算子，以同时提取信号中的正、负脉冲。

形态梯度（MG）为信号f（n）分别经过结构元素g（m）膨胀和腐蚀后的差分，其表达式为：

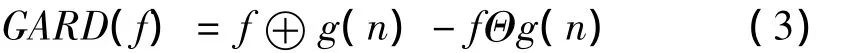
在图像处理中，MG常用来在图像中进行边沿检测。如果某一点处的梯度值大，则表示在该点处图像的明暗变化迅速，从而可能有边沿通过。在一维信号处理中，形态梯度算子可用来检测加于稳态信号上的暂态信息，它同时考虑了信号的正、负脉冲，是凸显脉冲信息的有力工具，可以有效的检测出脉冲的位置，较好的保留脉冲的形状。

1.3 结构元素

除了形态学变换方式的选择外，结构元素的选择对信号处理结果也有很大影响。常用的结构元素有直线、曲线（如二次，三次等）、三角形、圆形和其他多边形（如钻石形，六角形等）及其组合等。

最简单且最常用的结构元素为扁平型结构元素，即结构元素的幅值为零。使用扁平结构元素可以避免对信号幅值的修改，比非零结构元素更能直观准确地提取待处理信号的形状特征，这也符合形态学方法最朴素的出发点。另外，基于扁平结构元素的形态学运算的计算量显然会进一步减小。在本文的研究中，结构元素取为扁平结构元素。

1.4 多尺度形态学变换

多尺度形态学最初是基于形态学结构元素的分解而提出的，目的是提高大尺寸结构元素形态学运算速度和扩展形态学图像处理方法的应用范围。对于一维信号的多尺度形态学分析，只需要对单位结构元素进行膨胀就可以得到多尺度形态学分析的结构元素。

假设g为单位结构元素（本文取为g={0，0，0}），令sg为尺度s下的结构元素，且sg为g经过s－1次自身的膨胀所得：

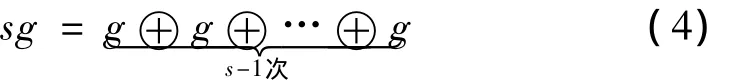
在不同尺度下采用结构元素对信号f的膨胀和腐蚀分别为：

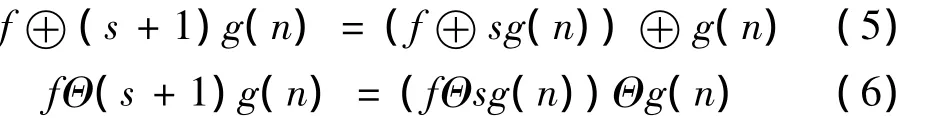
1.5 自适应多尺度形态梯度变换

为解决单尺度形态梯度变换存在的问题，本文提出了自适应多尺度形态梯度变换。其主要思想是，利用大小不同的结构元素提取信号冲击特征，小尺寸的结构元素去噪声能力弱，但能保留到好的信号细节，大尺寸的结构元素去除噪声能力强，但会模糊信号边界，因此将各种不同尺度下的信号结合起来可提取出较理想的冲击特征。为了提高抗噪声能力，可将大尺度的权重取得大一些，小尺度取得小一些，由此即可得到抗噪性能和细节保持兼顾的冲击特征信号。

首先采用多尺度结构元素分别对信号进行形态梯度变换，得到s个尺度下系列处理信号：

然后运用多尺度合成算法得到最终的梯度信号：

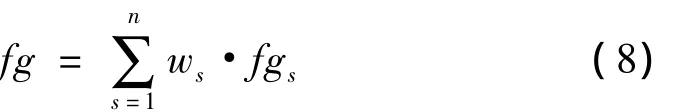
其中ws为各尺度信号的权重，其计算过程如下，首先计算各尺度下的形态梯度信号fgs，计算fgs与原信号之间的差值：

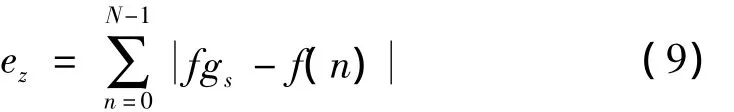
则ws可由下式所得：

由式（9）、式（10）可以看出，小尺度下信号的权重较小，大尺度信号权重稍大，由此即可保持细节又可有效的抑制噪声。

2 仿真信号分析

采用如下仿真信号进行试验分析，采样频率为2 048 Hz，采样时间为1 s：

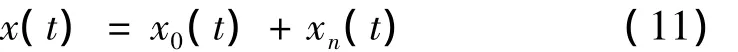
其中x0（t）为周期性脉冲衰减信号，频率为32 Hz，每周期衰减函数为 e－100000·t·cos（2π·1 000·t）；xn（t）为高斯白噪声。

图1（a）为仿真信号的时域波形，图1（b）为仿真信号的频谱图。由于强噪声信号的干扰，无论从时域图还是频谱图中很难看出脉冲信号的周期特征。图2为仿真信号包络及其频谱图。从图2中可以看出脉冲信号的冲击特征频率，但由于噪声的作用，时域与频谱图中脉冲信号的周期特征不是非常明显，且频谱非常杂乱。

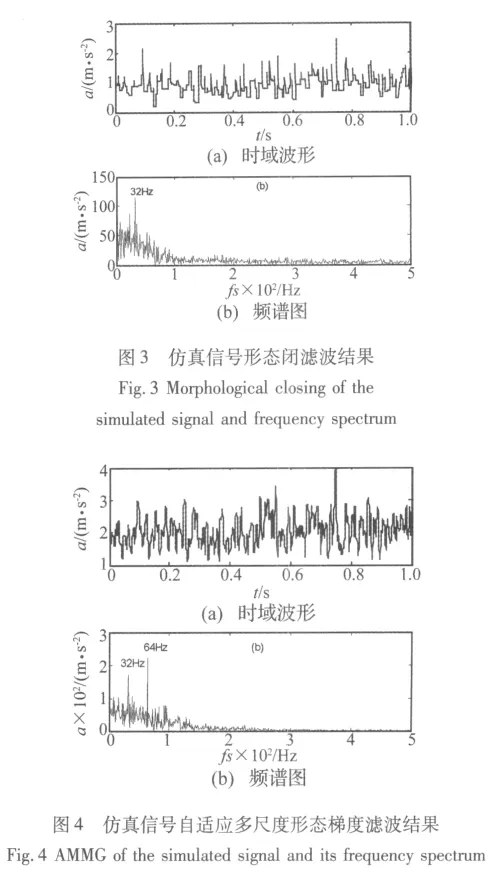
图3为采用尺度为5的扁平结构元素的形态闭变换对仿真信号处理的结果，从图3（a）中可以看出，信号的时域波形损失了大量的细节，存在着较大的畸变，其频谱中只有冲击特征频率一倍频的比较明显，且存在着一定的干扰。

图4为采用自适应多尺度形态梯度变换对信号的处理结果，从图4（a）可以看出，与形态闭变换相比，AMMG能够较好的保留信号的冲击细节特征，与包络解调方法相比，AMMG具备了很好的降噪特性，因此，从图4（b）中可以很明显的看出冲击特征频率的一倍和二倍频，且杂频明显比包络、形态闭少。

3 滚动轴承故障信号分析

为验证形态梯度滤波的有效性，本文采用实测的轴承故障信号进行检验。轴承振动加速度数据信号来自于Case Western Reserve University（CWRU）轴承数据中心网站。模拟的轴承故障主要包括内圈故障和外圈故障两种类型。

滚动轴承的型号为SKF 6205，轴承的局部损伤是由电火花机分别在轴承内圈和外圈人工加工制作，直径为0.177 8 cm，转速为1730 r/min，载荷为2.25 KW，转频为28.83 Hz，轴承内圈和外圈故障的特征频率分别为156 Hz和103.3 Hz。由于原始轴承故障信号比较理想，为验证本文提出方法的有效性，本文在原始信号基础上添加了方差为0.3的高斯白噪声。图5为轴承内圈和外圈故障的振动加速度信号。其中图5（a）为内圈故障信号，图5（b）为外圈故障信号。

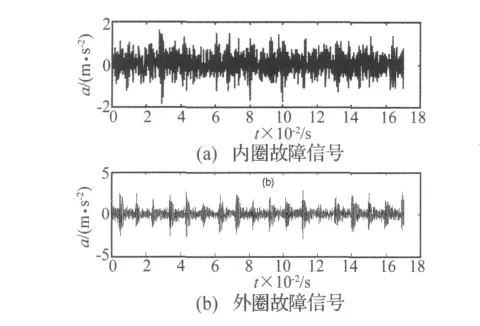
图5 滚动轴承原始故障振动加速度信号Fig.5 Vibration signal of bearing with inner race defect and outer race defect

图6为采用包络分析解调法对轴承内圈故障信号处理的结果，从图6（a）可以看出，包络分析解调方法不具备降噪的功能，其时域波形信号受噪声干扰很大，在频谱上内圈故障的冲击特征频率虽然比较明显，但存在着大量的高频干扰。

图7为采用尺度为10的扁平结构元素的形态闭变换对内圈故障信号处理的结果，从图7（a）中可以看出，处理后信号基本不受噪声的干扰，但信号的时域波形由于损失了大量的细节信号而存在着较大的畸变，因此其频谱也存在着一定的干扰。

图8给出了采用自适应多尺度形态梯度变换的内圈故障信号处理结果，与图6、图7相比，图8（a）给出的信号即抑制了噪声又保留了信号的细节，非常清晰而又不失真的提取出轴承故障信号的脉冲特征，在频谱图8（b）中，内圈故障信号的冲击特征频率的一倍和二倍频非常明显，且受杂频干扰较小。

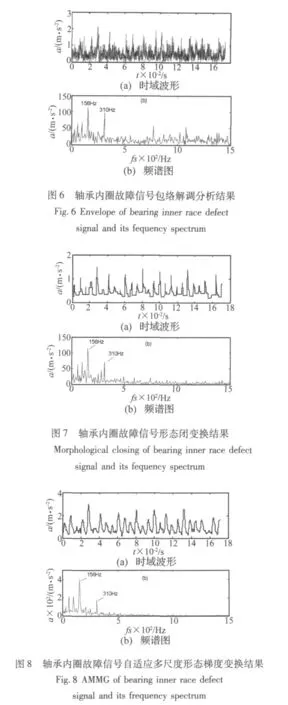
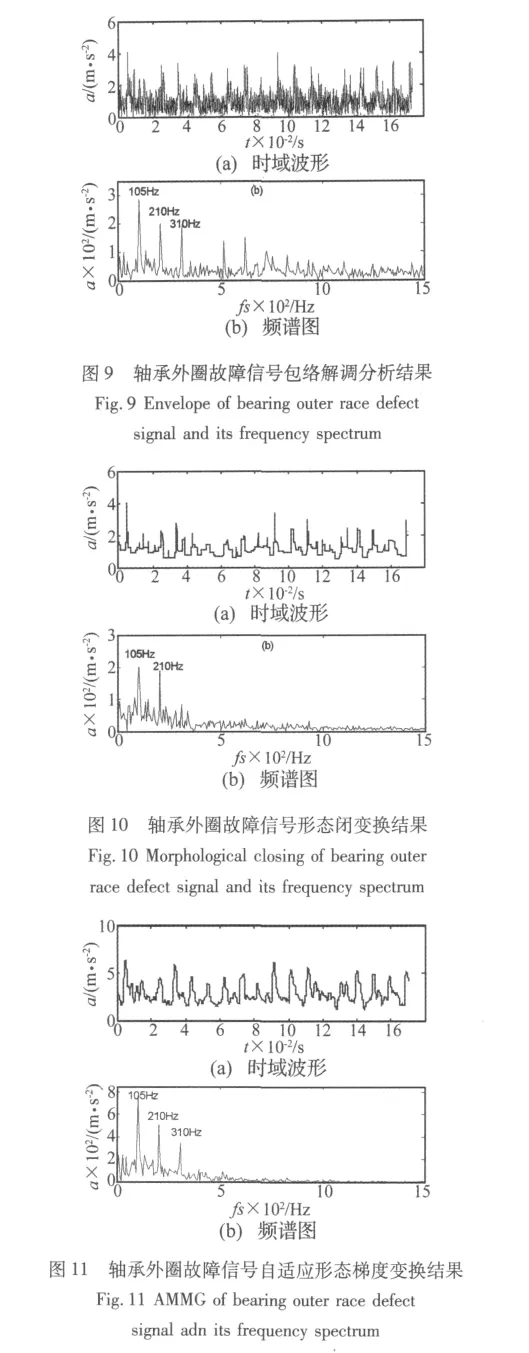
图9、图10和图11分别给出了采用包络解调分析、形态闭变换和自适应多尺度形态梯度变换对轴承外圈故障信号进行处理的结果，对比三种方法可以看出自适应多尺度形态梯度变换在冲击特征提取上具有很大的优势，轴承外圈故障信号的冲击特征频率的一倍和二倍频非常明显，且受杂频干扰较小。

4 结论

数学形态学为数字信号处理提供了一种新的快速分析手段，本文提出了一种自适应多尺度形态梯度变换用于强噪声背景下脉冲信号的提取方法，并与传统的包络解调分析方法和另一种近来提出的基于数学形态学的形态闭变换方法进行了对比，仿真信号和实测轴承故障信号的处理验证了自适应多尺度形态梯度变换的有效性和优越性。

与包络解调分析方法相比，自适应多尺度形态梯度变换在提取脉冲包络信号的同时又降低了噪声的干扰；与形态闭变换相比，自适应多尺度形态梯度变换在抑制噪声的同时较好的保持了信号细节；此外，自适应多尺度形态梯度变换同时计算了信号的正负脉冲，因此能够在强噪声环境下更有效的提取出微弱的脉冲信号，从而为轴承故障特征提取和故障诊断提供了一种更为有效的分析方法。

［1］Rubini R，Meneghetti U.Application of the envelope and wavelet transform analyses for the diagnosis of incipient faults in ballbearings［J］. MechanicalSystemsand Signal Processing，2001，15（2）：287－302.

［2］Maragos P，Schafer R W.Morphological filters-partⅡ：their relations to median，order-staistic，and stack filters［J］.IEEE Transactions on Acoustics， Speech， and Signal Processing，1987，ASSP－35（8）：1170－1184.

［3］Maragos P，Schafer R W.Morphological filters-partⅠ：their set-theoretic analysy and relations to linear shift-invariant filters［J］.IEEE Transactions on Acoustics，Speech，and Signal Processing，1987，ASSP－35（8）：1153－1169.

［4］ Serra J，Vincent L.An overview of morphological filtering［J］.Circuits Systems and Signal Processing，1992，11（1）：47－108.

［5］Ma J，Xu Y，Wang Z P.Power transformer protection based on transientdata using mathematicalmorphology［J］.Proceedings of the Chinese Society of Electrical Engineering，2006，26（6）：19－23.

［6］Sun Y，Chan K L，Krishnan S M.ECG signal conditioning by morphological filtering［J］. Computersin Biology and Medicine，2002，32（6）：465－479.

［7］Nikolaou N G，Antoniadis I A.Application of morphological operatorsas envelope extractors for impulsive-type periodic signals［J］.Mechanical Systems and Signal Processing，2003，17（6）：1147－1162.

［8］杜秋华，杨曙年.形态滤波在滚动轴承缺陷诊断中的应用［J］.轴承，2005，21（6）：27－31.

［9］胡爱军，唐贵基，安连锁.基于数学形态学的旋转机械振动信号降噪方法［J］.机械工程学报，2006，42（4）：127－130.

［10］章立军，杨德斌，徐金梧，等.基于数学形态滤波的齿轮故障特征提取方法［J］.机械工程学报，2007，43（02）：71－75.

［11］章立军，阳建宏，徐金梧，等.形态非抽样小波及其在冲击信号特征提取中的应用［J］.振动与冲击，2007，26（10）：57 －61，85.