基于姿态变化的列车侧风安全性研究的新方法

崔 涛， 张卫华

（西南交通大学 牵引动力国家重点实验室，成都 610031）

列车依靠特有的轮轨接触关系沿轨道近地面运行，其长细比远大于其他交通工具，易受到侧风的干扰。强侧风导致列车脱轨，乃至倾覆的事故严重危害了旅客的生命财产安全。侧风环境下列车的姿态发生变化，其气动载荷发生变化［1］，进而侧风对列车安全性的影响也随之改变。采用计算流动动力学（CFD）与多体动力学（MBSD）联合同步仿真的方法可以得到列车的姿态变化及其气动载荷。但该方法MBSD程序计算一步，CFD程序也要计算一步。CFD程序的计算量庞大，耗时很长，这是目前列车侧风研究中不考虑姿态变化［2－7］的原因之一。而侧风作用下，列车最终自适应到一个相对稳定的状态，考虑姿态变化，最终关心的还是稳定姿态下的列车气动特性。因此，本文设计一种快速高效的仿真方法，首先确定侧风作用下列车的稳定姿态以及气动载荷，然后进行列车运行安全性分析。

1 计算方法

首先，分别建立列车侧风计算流体动力学模型和列车多体系统动力学模型。然后，进行列车侧风计算流体动力学和列车多体系统动力学的联合仿真，其中列车系统动力学模型不考虑轨道激励，侧风环境下列车以平衡状态逐步逼近最终平衡状态。最后将此气动载荷加载到列车多体系统动力学模型，并考虑轨道激励，进行动力学分析，评价侧风环境下列车的安全性指标。

1.1 侧风CFD模型

建立用于侧风特性计算的几何模型，确定合理的计算域，然后采用适当网格类型对整个计算域进行离散。接着根据守恒定律建立控制方程，见式（1）。在控制体积上积分控制方程，见式（2），如果考虑可压缩性，采用理想空气，还需添加完全气体状态方程，见式（3）。CFD中采用动态网格来适应列车姿态的变化，因此还需求解体积守恒方程，见式（4）。采用合理的离散格式将控制体界面的物理量通过插值的方式由节点的物理量来表示，建立离散代数方程，见（5）。最后，通过合理求解方法对代数方程组求解，如SIMPLE算法等［8］。

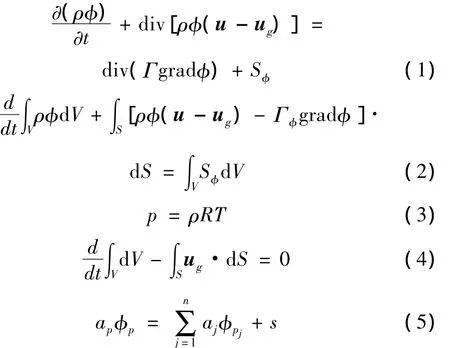
式中：φ为流场通量，φ=1、流速u、温度T、湍动能k、湍动能耗散率ε时，方程（1）分别表示连续性方程、动量方程、能量方程、湍动能k方程和湍动能耗散率ε方程；u为流体流动速度，ug为控制体的界面运动速度；Гφ和Sφ分别表示广义离散系数及广义源项；div、grad分别表示散度、梯度；V为控制体的体积，A为包围该体积的封闭面面积；p为压力，R为气体常数。a和s根据时间和空间差分格式的不同而不同。

1.2 列车MBSD模型

列车MBSD模型是一个由弹性原件连接的多体系统，主要包括轮对、构架、车体以及悬挂系统和车钩装置等弹性元件。根据不同车型，模型还可以考虑轴箱转臂、摇枕，弹性元件还可能包括抗蛇形减振器、车间减振器等。各部件均不考虑各部分的弹性变形，视为刚体。车体、构架以及轮对可以根据需要采用不同的自由度数。将作用在列车车体表面上的气动压力等效为作用在车体质心上的集中力和力矩，如图1所示。

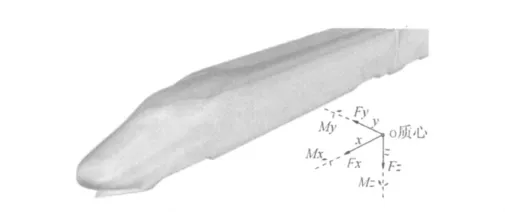
图1 气动载荷Fig.1 Aerodynamic load

通过Lagrange原理可以建立列车系统动力学方程为：

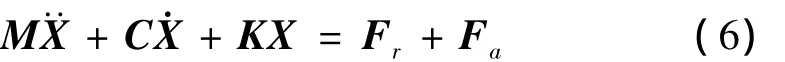
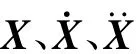
1.3 联合仿真方法

联合仿真总的思路如下：仿真开始时，CFD和MBSD中列车处于静平衡姿态；接着CFD进行计算，流场达到稳定的状态，CFD暂停，将气动载荷输入到MBSD开启计算直到列车多体系统达到平衡状态，MBSD暂停；然后将姿态变化量输入到CFD进行两个步骤的计算，每个CFD计算步包括两个子步，第一子步按照姿态变化量对列车姿态进行调整，第二子步计算该姿态下列车的气动载荷；接着再将此气动载荷传递给MBSD并开启计算直到列车达到平衡；如此反复直到列车的姿态和气动载荷达到稳定时，仿真结束。如图2所示。

MBSD中列车在一定的气动载荷达到平衡，列车达到平衡的判断依据为：一定时间段内列车振动的速度和加速度均小于10－4。CFD中采用动态网格技术以适应流场中列车姿态的变化，为了保证网格质量，列车姿态不宜发生快速的大变化，但为节省计算时间，又必须保证一定的调整速度。故应根据网格大小和时间步长，选择适当的姿态调整速度。

仿真开始时列车处于静平衡状态，气动载荷变化较大，列车姿态发生较大的变化，随着仿真的进行，列车姿态的调整量降低。MBSD中气动载荷较大的变化可能会引起列车的振荡，不利于计算的收敛。同时较大的姿态变化将引起流场的较大的变化，CFD在完成姿态调整后，流场的再次稳定下来需要较长的时间，所以CFD计算列车新姿态气动载荷的时间相对较长。因此仿真初始阶段应该控制气动载荷和姿态变化的速度。当仿真达到一定阶段时，气动载荷和姿态变化较小时，MBSD中列车很快达到平衡，CFD中姿态调整所需时间较短，计算新姿态所需的时间也较短。应降低CFD计算列车新姿态气动载荷的时间，从而保证列车与侧风整个大系统快速平衡。

2 算例分析

采用上述方法对20 m/s侧风环境下以300 km/h运行于高架桥上的列车的安全性进行仿真分析。其中，侧风垂向作用于车体侧墙，高架桥高度为6 m，列车运行在高架桥迎风侧的线路上，线路的几何不平顺采用京津线路谱。

2.1 计算模型

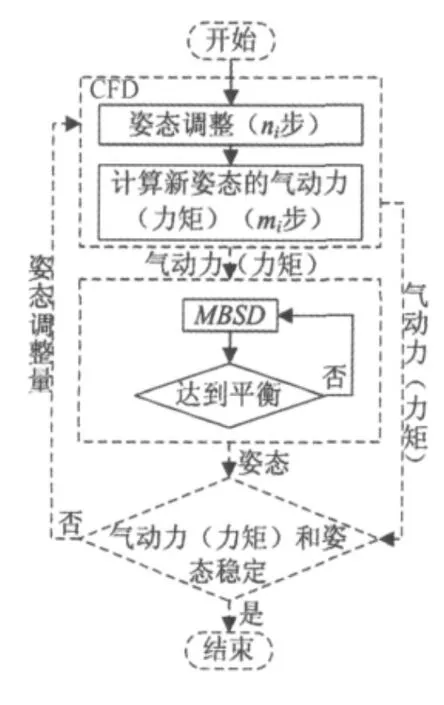
图2 （a） 联合仿真流程图Fig.2（a）Co-simulation flowchart

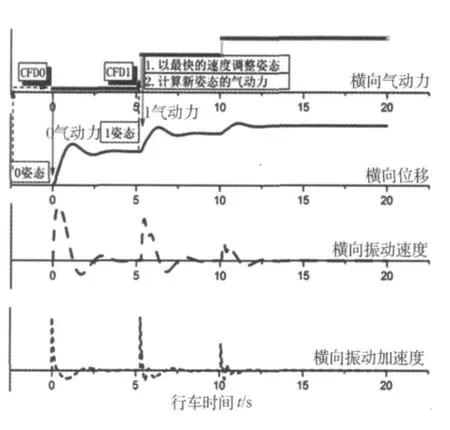
图2 （b） 仿真联合方法示意图Fig.2（b）Co-simulation schematic

分别建立列车侧风CFD模型和列车MBSD模型，然后按照以上方法对两者进行联合仿真。两个模型均采用头车、尾车、中间车三车编组。为了简化计算，列车侧风CFD模型中，对列车外形做了一定的几何简化，忽略转向架、受电弓、车体连接部位等细部结构。

2.1.1 列车侧风CFD模型

列车运行速度和侧风风速的合成速度为U=85.70 m/s，其马赫数为 0.25，小于 0.3 Ma，计算中忽略空气介质的可压缩性。列车车宽w=3.38 m，空气在20°时的运动粘度v=15.08×10－6m2/s，则 雷 诺 数 Re =Uw/v=1.92 ×107，列车周围的流场呈湍流状态，湍流模型采用标准k－ε双方程模型，近壁区采用壁面函数法进行处理。

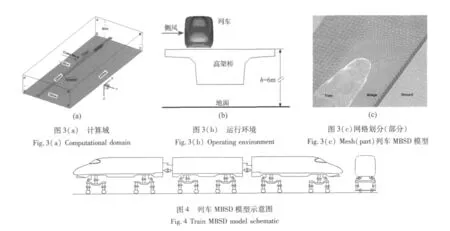
整个计算网格区域为450 m×230 m×80 m，分为2个区域：近车区，外围区。近车区为动态网格区域，采用非结构四面体网格，网格可以随着列车姿态的变化而变形或者重划分。外围区采用结构规则六面体网格划分。如图3所示。

2.1.2 列车MBSD模型

列车MBSD模型是一个由弹性元件连接的多体系统，如图4所示。模型中每个车体具有6个自由度，每个构架具有6个自由度，每个轴箱具有1个自由度，每个轮对具有4个独立自由度，整个模型具有126个自由度。车轮踏面采用LMA磨耗型踏面，钢轨采用60公斤标准钢轨。模型中除考虑了轮轨非线性接触外，还考虑了抗蛇行减振器、横向止挡以及钩缓和车间减振器的非线性。侧风气动载荷由CFD逐状态提供。

2.2 计算结果

列车在侧风的作用下以平衡状态逐步调整到稳定姿态。将稳定姿态下的气动载荷作为列车MBSD模型的气动激励，并考虑线路的几何不平顺，进行动力学分析，得到侧风作用下列车的安全性指标。

2.2.1 计算速度分析

联合同步仿真，MBSD每计算一步，CFD就需要计算一步。而采用本文方法，侧风作用下，列车逐状态的调整到稳定姿态，每个气动载荷下列车系统均达到平衡，每个列车姿态下流场也都达到稳定，CFD不需与MBSD同步，只需在列车系统达到平衡后进行列车姿态调整和姿态调整后的气动力计算，计算时间步大大减少，如图5所示。可见该仿真方法大大的降低了CFD的计算量，从而有效节省整体的计算时间。

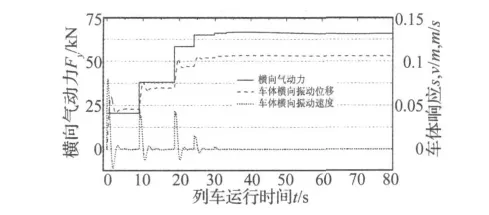
图5 姿态与气动力Fig.5 Attitude and aerodynamic force

2.2.2 姿态与流场变化

侧风作用下，列车最终达到稳定姿态，其姿态变化量见表1，流场也达到稳定状态，列车与流场整个大系统达到稳定。如图5所示，仿真后期气动载荷和列车姿态基本保持不变。相对于初始姿态列车姿态发生了一定的变化，相应的列车外表面上的气压以及列车附近的流场也发生了一定的变化。图6－图7给出了两种姿态下的压力分布。

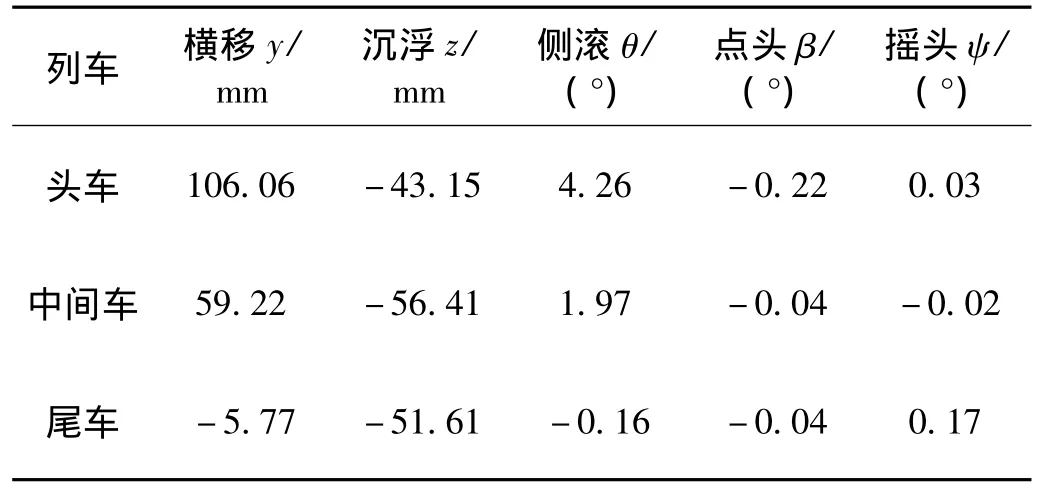
表1 侧风下列车的姿态变化Tab.1 The change of train attitude in side wind

图6 Fig.6（a）Pressure distribution of initial attitudeFig.6（b）Pressure distribution of stable attitude

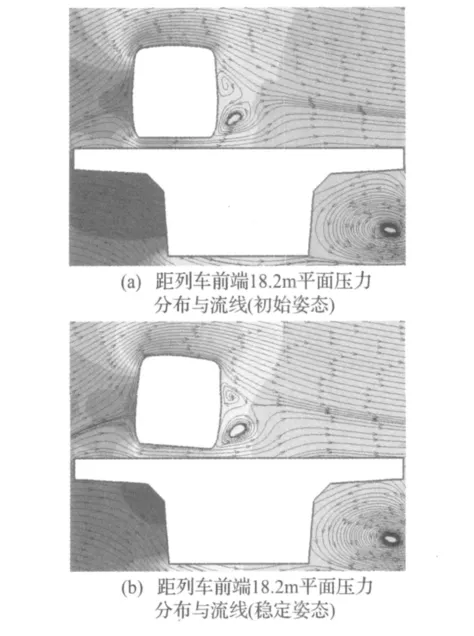
图7 Fig.7（a）Pressure distribution and streamline of the face where is 18.2 m from leading end（initial attitude）Fig.7（a）Pressure distribution and streamline of the face where is 18.2 m from leading end（stable attitude）

如图 7（b）所示，由于头车的侧滚，迎风侧侧墙倾斜，气流较易顺势上升，因此迎风侧侧墙正压值减弱；同时由于迎风面积的改变，背风侧侧墙的负压有所增强。另外由于车体底面的倾斜，头车车体底面与高架桥之间的距离有所减小，头车车体底面负压减弱；列车顶面的负压有所增强。如图8所示。

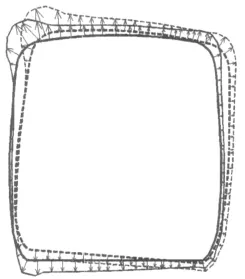
图8 距前罩18.2 m处列车的姿态变化及压力分布情况Fig.8 Pressure distribution of the profile where is 18.2 m from leading end

2.2.3 气动载荷变化

由于列车表面气压的变化，列车的气动载荷也将发生变化。头车迎风面积的变化增大了列车的横向气动载荷，头车底面迎风面积的变化增大了列车的升力。中间车、尾车的气动载荷也发生了相应的变化，如图9所示。姿态变化所引起气动载荷变化的规律和文献［1］一致。

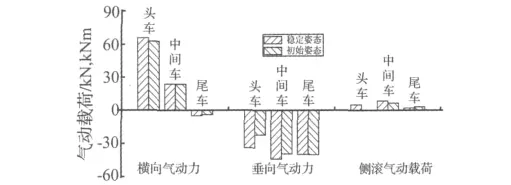
图9 列车气动载荷Fig.9 Train aerodynamic load

2.2.4 列车安全性指标

将以上所得稳定姿态的气动载荷加载到列车MBSD模型，并考虑轮轨几何不平顺，进行列车动力学分析，考察列车的安全性指标：脱轨系数Q/P、轮重减载率dP/P、车轮垂向最大作用力Hmax以及轮轨横向作用力Pmax，从而确定侧风环境下列车运行的安全性。侧风下列车各安全性指标如表2所示。

表2 列车安全性指标Tab.2 Safety indexes of train

3 结论

侧风环境下列车姿态发生变化后，气动载荷也随之发生变化，进而侧风对列车安全性的影响也发生变化。采用本文所述的联合仿真方法，列车在侧风的作用下以平衡状态逐步到达稳定姿态，并获得稳定姿态下的气动载荷，从而进行列车侧风安全性分析。该方法忽略侧风环境下列车的自适应运动过程，只关心最终姿态，其CFD计算量得到有效的缩减，仿真速度较同步仿真提高15倍～20倍左右，大大的节约了计算时间，为考虑姿态变化的列车侧风安全性研究提供了一种快速有效的研究方法。

［1］ Baker C J，Jones J，Lopez-Calleja F，et al.Measurements of the cross wind forces on trains［J］.Journal of Wind Engineering and Industrial Aerodynamics，2004，92（7）：547－563.

［2］ Carrarini A.Reliability based analysis of the cross-wind stability of railway vehicles［J］.Journal of Wind Engineering and Industrial Aerodynamics，2007，95（7）：493 －509.

［3］Suzuki M， Tanemoto K， Maeda T. Aerodynamic characteristics of train/vehicles under cross winds ［J］.Journal of Wind Engineering and Industrial Aerodynamics，2003，91（1）：209－218.

［4］ Sanquera S，Barrea C，De Virela M D，et al.Effect of cross winds on high-speed trains：development of a new experimental methodology［J］.Journal of Wind Engineering and Industrial Aerodynamics，2004，92（7）：535 －545.

［5］任尊松，徐宇工，王璐雷，等.强侧风对高速列车运行安全性影响研究［J］.铁道学报，2006，28（6）：46－50.

［6］黄 林，廖海黎.横向风作用下高速铁路车桥系统绕流特性分析［J］.西南交通大学学报，2005，40（5）：585－590.

［7］高广军，田红旗，姚 松，等.兰新线强横风对车辆倾覆稳定性的影响［J］.铁道学报，2006，26（4）：36－40.

［8］ Versteeg H K， Malalsekera W. An Introduction to computational fluid dynamics［M］.北京：世界图书出版公司，2000：21－25.