一种扬声器异常音的时域特征检测方法

韦峻峰， 杨 益 ， 温周斌 ， 冯海泓

（1.中国科学院 声学研究所东海研究站，上海 200032；2.中国科学院 声学研究所嘉兴工程中心，浙江嘉兴 314006）

在扬声器生产过程中常产生各种缺陷。以动圈扬声器为例，通过测量阻抗曲线或极性等常规测试项目，可以检测出音圈短路、断路、焊接不良和反接等缺陷。而因磁隙、防尘帽或其他部件混入杂质，因部件发生共振、摩擦或碰触现象或因胶水粘接不良等缺陷导致的异常音故障（Rub and Buzz）则难以通过常规参数检测。有异常音故障的扬声器在工作时会产生除激励信号频率之外的声音，从而导致回放音质恶化，因此在产品出厂前需要由有经验的听音员反复听音检查。

使用机器替代人耳检测异常音可以给出更为客观的结果。早期的研究采用离散对数扫频信号作为激励信号，对采集到的声响应信号滤波并求总谐波失真，其结果用于检测异常音［1］。然而，由扬声器结构引起的固有非线性失真的幅度远大于异常音失真的幅度，因而难以通过总谐波失真检测异常音故障［2］。此外，由于扫频频率不连续，扫频频率点外的谐振现象可能无法激励。近年来许多检测异常音的新方法被提出，Shane等提出高阶谐波失真（High-order harmonic distortion，缩写为 HOD）响应可用于异常音检测［3］。Farina提出使用连续对数扫频信号作为激励，同时测量线性冲激响应和各阶谐波失真的冲激响应的算法［4］。该激励信号的频率随时间连续变化，可以更有效地激发被测频率范围内的谐振现象。后来该方法也被用于异常音检测［5］。根据人耳对声音的感知机理，Leonhard提出通过检测异常音故障扬声器的声信号中脉冲能量的斜率，实现了多种故障的检测［6］。国内学者提出了基于时频分析［7，8］、小波滤波的噪声检测方法［9］。此外，一种客观评价音频编解码器对音质的损失的音质感知评价方法（Perceptual Evaluation of Audio Quality）亦被用于扬声器失真评价［10，11］。

在分析有异常音故障的扬声器的时域响应波形中，可观察到有微弱的异常音振动特征叠加在正常响应之上。不同的异常音故障对应的振动特征是不同的，而振动特征在异常音故障分类中有重要的作用。基于傅里叶变换的处理方法虽然得到了异常音的频域特征，但叠加在激励信号上的脉冲在频域被展宽，损失了振动特征。采用时域处理方法可能是一种更为有效的特征检测方法。

基于上述讨论，本文提出了一种时域的特征检测方法。首先对扬声器在连续对数扫频信号激励下的声响应信号进行经验模态分解（Empirical mode decomposition，缩写为EMD），之后对分解出的各阶本征模态函数（Intrinsic mode functions，缩写为IMF）进行去混淆处理，得到各子带内包含异常振动信息的模态函数。通过仿真验证和实验验证，证明IMF的时域特征可用于异常音故障的检测与分类。

1 理论分析

1.1 异常音的种类

动圈扬声器种类繁多，小至手机中的微型扬声器，大至舞台音箱中的低音单元，但其结构有类似之处。大多数动圈扬声器参与振动的部分由振膜、防尘罩、折环、定心支片和音圈组成，其他部件有导磁柱、导磁板、盆架和接线柱。常见的异常音种类如下：

（1）音圈摩擦（Coil Rubbing）音：在扬声器加入激励时，因安装不正确导致音圈或音圈骨架与磁隙周期性接触而产生该异常音。此外，磁隙中的杂质也可能产生音圈摩擦音。在使用一段时间后，音圈摩擦故障很可能导致扬声器损坏。

（2）部件摩擦（Buzzing）音：当部件粘接不良时，部件之间可能发生相对运动。粘接不良的部件在外力驱动下按部件的自身特性产生与激励信号不一致的振动。

（3）异物碰触（Loose particles）音：扬声器振膜与其他杂质发生碰撞或防尘罩内有异物时，发出随机的脉冲声。有时异物会卡在部件当中导致故障现象暂时消失。

（4）部件共振（Resonance）音：固定扬声器的箱体、扬声器测试时使用的消声箱盖板等外部部件在某些特定频率下会发生共振。

（5）漏气（Air leakage）音：扬声器箱体上由于粘接出现问题导致声音发生变化。漏气问题通常可以由频响、阻抗等参数或其他专用方法［12］检测出来。

1.2 人耳检测异常音的机理

人耳对不同频率的声音敏感程度不同。在声级计中，这种差异通过滤波器组和加权实现［13］，在助听器和人工耳蜗中也采用了类似的结构。

正如1.1节所述，异常音多为摩擦声、碰触声，这些声音的频带很宽。在文献［10］中给出了一个例子，被测扬声器在100 Hz激励信号下发出声压级120 dB的纯音和异常音，其声响应的幅度谱如图1。为便于观察，在图中基频响应用“Fund”标注，n阶谐波响应用谐波的阶数标注。可见，其19阶以上的谐波幅度高于100 Hz掩蔽曲线，因而不被激励信号掩蔽。同时，其19次以上的谐波幅度也高于听阈曲线，因而可以被人耳分辨出来。

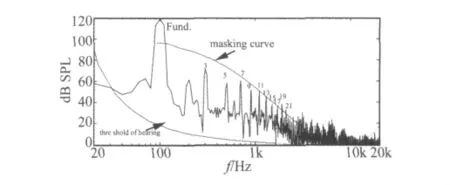
图1 异常音故障扬声器的声压级幅度谱及掩蔽、听阈曲线Fig.1 SPL Spectrum of loudspeaker with Rub＆Buzz defect，perceptual masking curve and the threshold of hearing

Zwicker的研究表明，当脉冲持续时间大于100 ms时，人耳感受到的响度与脉冲持续时间不相关；而当脉冲时间小于100 ms时，脉冲时间越短，人耳感受到的响度越低［13］。如前文所述，某些异常音的发生具有随机性，其产生的脉冲幅度和持续时间不确定，人耳听测可能造成漏检，因此往往需要反复听测以降低漏检概率。

1.3 经验模态分解（EMD）

由Huang提出的EMD方法是一种分析非线性、非平稳信号的工具，在振动信号处理领域有着广泛的应用［14］。扬声器自身的结构特点及材料的物理特性决定了它是一个非线性系统。而对于有异常音故障的扬声器，其声响应含有非平稳的失真成分，因而可用EMD法分析。

EMD与小波滤波器组类似，随着分解算法的推进，代表着高频到低频振动模态的数个IMF被分解出来［15］。在黄海的研究中发现，通过数次EMD计算可求出固有非线性失真产生的低次谐波振动模态［16］。与此不同的是，在对有异常音缺陷的扬声器的声响应进行EMD计算时，异常音缺陷产生的是高次谐波振动模态，其主要出现于IMF1中。由于异常音频带较宽，异常音信号也会分散到其他IMF中。

EMD算法可参见文献［14］，本文不再赘述。

1.4 激励信号的选择

不同激励信号下，扬声器发出异常音的显著程度是不同的。异常音通常为宽带信号，若使用频率特征类似的宽带信号（如多频信号或噪声）作为激励则难以区分正常的响应与异常音响应。

人耳听音时通常选用正弦扫频信号作为激励。在任意时刻，激励信号为窄带信号。此时正常扬声器的响应主要集中在基频，对应着滤波器组中某个滤波器；发出异常音的扬声器除了检测到基频响应外，还存在高阶谐波响应或噪声，对应着滤波器组中多个滤波器。

与人耳听音类似，后续的仿真与实验验证中均选用连续对数扫频信号作为激励。连续对数扫频信号的表达式为：

其中，L=T/ln（f2/f1），f1与f2分别为扫频的起始频率和终止频率，扫频时长为T。可以看到，扫频信号频率随时间t呈指数连续变化且存在唯一对应关系：

1.5 去混淆处理

由于激励信号的频率范围很宽，在EMD计算时响应信号被划分为由高频到低频的多个模态。噪声和可能存在的异常音信号亦被分解到各模态中。由于异常音信号的幅度远小于声响应信号的幅度，分解在各个模态中的响应信号将淹没异常音信号，这样的现象称为混淆现象。

被混淆的信号无法用于异常音检测，因此，需要通过瞬时频率的特征排除被混淆信号。扬声器的声响应瞬时频率与激励信号的瞬时频率是一致的，而噪声和异常音的瞬时频率与激励信号的瞬时频率不相关，在测量频带范围内随机变化。根据这一特征，可以通过IMF的瞬时频率与激励信号瞬时频率相减的方式，得到瞬时频率差曲线。若瞬时频率差小于某门限值，则认为该部分IMF发生了混淆，求得结果不是异常音信号；若瞬时频率差呈噪声状，说明检测结果为异常音信号或环境噪声。

瞬时频率可由希尔伯特变换求得，函数f（t）的希尔伯特变换可表示为：

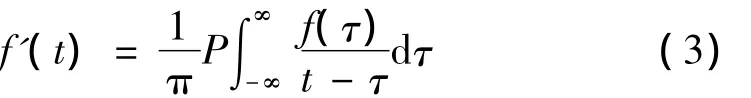
积分符号前的P表示进行柯西主值积分。构造解析信号z（t），该信号由f（t）和f'（t）构成，以指数形式表示为：

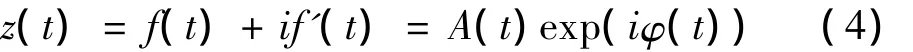
其中瞬时幅度为A（t），瞬时相位为φ（t）：

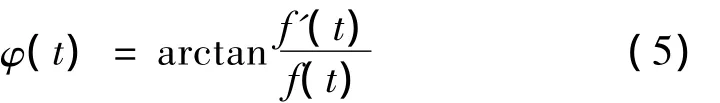
那么瞬时频率为瞬时相位对时间求导，即

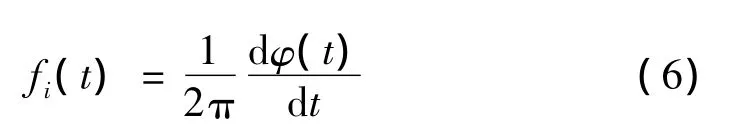
2 仿真验证

2.1 验证方法概述

扬声器的异常音故障具有很强的随机性，故障发生的频率和强弱可能随外界条件发生变化。然而异常音具有特定的时域和频域特征。目前已知的异常音特征有：声响应信号的时域波形上有尖峰，频域上有能量较大的宽频带噪声或20阶以上谐波失真等。通过仿真验证，可以客观地考察算法对这些噪声信号的敏感程度。

仿真验证的流程如下：首先建立扬声器的仿真模型得到理想的声响应。其次，在声响应信号上加入噪声可得到模拟的合格扬声器的声响应，对其进行EMD计算，得到合格扬声器的IMF。在声响应信号上加入噪声和模拟的碰触、摩擦等异常音，对其进行EMD计算得到不合格扬声器的IMF。最后，通过比较IMF与模拟的异常音的特征，证明时域特征提取方法的有效性。

2.2 扬声器声响应仿真

考虑到扬声器的线性失真和固有非线性失真，在已知扬声器参数的条件下，可以通过状态空间模型仿真求出声响应信号。图2分别给出了仿真与实测的频响曲线。在频率为50 Hz～500 Hz范围内，仿真曲线与实际曲线结果差异在3 dB以内。

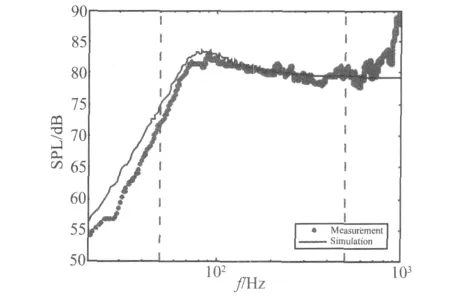
图2 仿真与实测频响曲线Fig.2 Frequency responses of simulation and measurement

2.3 合格扬声器声响应仿真

故障扬声器发出的异常音与激励信号幅度有关，通常异常音声压级在40 dB～60 dB［17］，而听音环境声压级在50 dB以下。检测设备的电噪声折算为声压级后约为20 dB，远小于环境噪声对检测结果的影响，因此不作单独考虑。

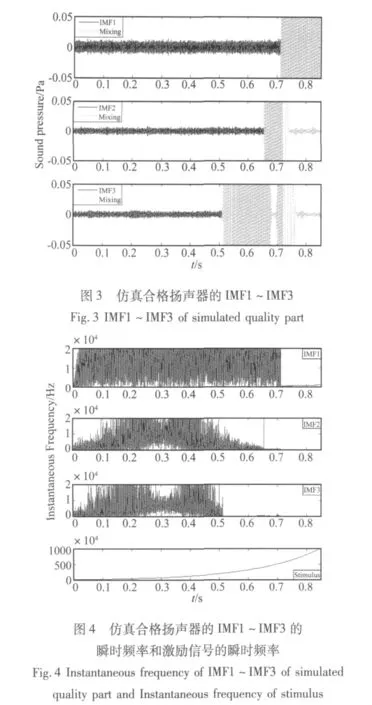
根据上述条件加入50 dB的噪声后，对合格扬声器进行EMD计算，得到的结果如图3。在IMF1的t＞0.7 s处，声响应信号的基频进入了等效滤波器的通带中，与噪声及异常音特征混淆在一起。对IMF求瞬时频率的结果如图4。由瞬时频率差可以确定IMF1～IMF3发生混淆的部分分别为t＞0.72 s、t＞0.66 s和t＞0.53 s，混淆部分在图3中用灰色表示。

2.4 模拟异常音故障

仿真中采用脉冲信号模拟异物碰触引起的冲击异常音，采用白噪声模拟音圈轻微摩擦时发出的摩擦异常音，采用激励信号的谐波模拟部件摩擦发出的30阶以内的谐波异常音。设异常音的声压级为60 dB，可构造出如图5（a）所示的带噪声的异常音时域波形。在0.20 s、0.43 s和0.65 s处为脉冲，0.29 s～0.37 s处为白噪声，0.48 s～0.56 s处为激励信号的3～30阶奇数阶谐波失真。将其与未加噪声响应相加，得到如图5（b）所示的波形。

对仿真中使用的声响应信号进行短时傅里叶变换，得到声响应时频图如图6。颜色越深表明信号幅度越大。图中可以观察到模拟的音圈摩擦和部件摩擦的特征，而由脉冲引起的失真特征则较为微弱。

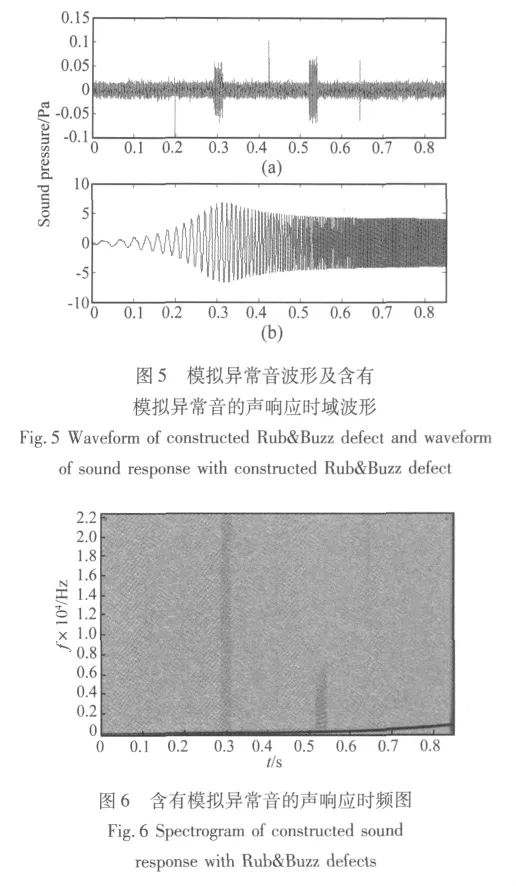
图7是对上述声响应信号进行EMD计算后得到的IMF1～IMF3，其灰色部分为发生混淆的部分。3个脉冲在IMF1中对应时刻被提取出来。白噪声覆盖在整个频带内，在IMF1～IMF3中均被提取。而3～30阶奇数阶谐波失真能量集中在800Hz以下，在 IMF2、IMF3中均有明显的特征。

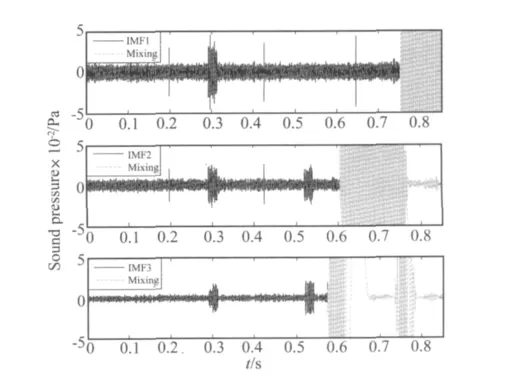
图7 含有模拟异常音的声响应的IMFFig.7 Intrinsic mode function of sound response with constructed Rub＆Buzz defects

比较图3和图7可发现，合格扬声器的IMF幅度是平坦的，而有异常音的IMF幅度有显著变化，且与模拟异常音时域波形有对应关系。仿真结果表明，EMD方法对于碰触、音圈摩擦等异常音特征是灵敏的。通过去混淆处理后的IMF的幅度加门限可以检测是否发生异常音故障。IMF包含着异常音故障的时域及频域特征。此外，EMD方法对于脉冲的灵敏程度要优于时频分析方法。

3 实验验证

3.1 实验装置

实验中选用了型号为96330的6英寸汽车扬声器，其额定功率25 W，阻抗4 Ω。被测扬声器共20只，其中合格扬声器、音圈摩擦、部件摩擦和异物碰触故障扬声器各5只。使用4 V扫频信号激励测试样品，先由工厂2位听音员共同确认故障类别，再通过实验装置采集声响应信号。实验装置如图8所示，测试软件可计算出声响应信号中的频响及高阶谐波失真曲线，并可导出声响应信号。使用本文方法对声响应信号处理后，将检测结果与高阶谐波失真曲线对比，以验证不同方法检测到的发生故障的频率点及故障强度是否一致。

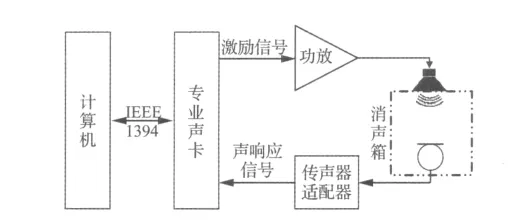
图8 实验装置Fig.8 Experiment equipment

由于使用了连续对数扫频信号作为激励，其时间与频率存在唯一的对应关系，响应信号的IMF的时间轴可被替换为频率轴，以考察发生故障的频率。

3.2 实验结果及分析

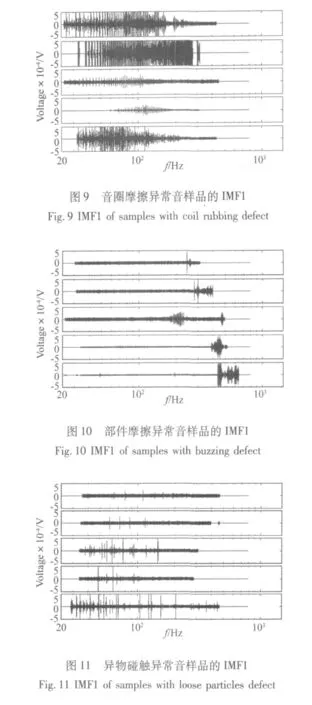
在20只扬声器样品中，5只音圈摩擦、5只部件摩擦和5只异物碰触的IMF1分别如图9～图11所示。5只合格扬声器的IMF1与图12类似，其包络是平直的，故不单独给出。

据人耳听音经验，音圈摩擦音常发生在扬声器共振频率处。如图9，在共振频率f0=73 Hz附近由于音圈的振幅达到最大，IMF1中提取出了密集而明显的尖峰。对于轻微音圈摩擦故障的样品，亦可观察到类似现象。此外，部件摩擦样品的IMF1在200 Hz后出现局部异常，异物碰触样品则在测试频率范围内出现随机的尖峰。可见，同一类故障的不同样本之间，IMF1具有相似的特征。

在20只扬声器样品中选出了4只具有代表性的扬声器，以便更清晰地观察异常音样品的IMF特征。将合格扬声器记为1#，有音圈摩擦异常音故障的扬声器记为2#，有部件摩擦异常音故障的扬声器记为3#，有异物碰触异常音故障的扬声器记为4#，结果如图12～图15所示。

对于频响曲线，合格扬声器与故障扬声器结果差别很小，无法用于检测异常音故障。而在IMF图中（虚线为故障检测门限）合格扬声器的IMF在虚线范围内，而发出异常音的扬声器的IMF幅度远大于门限。且从IMF1和高阶谐波失真曲线中可以观察到发生故障的频率及幅度具有对应关系。在500 Hz之后，由于发生了混淆导致IMF1无效，其相应部分被置零以避免误判。

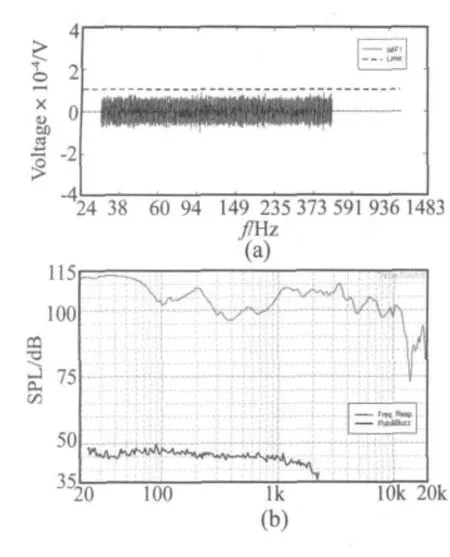
图12 1#（合格）样品的（a）IMF1；（b）频响及高阶谐波失真曲线Fig.12（a）IMF1，（b）frequency response and HOD of sample 1#（quality part）

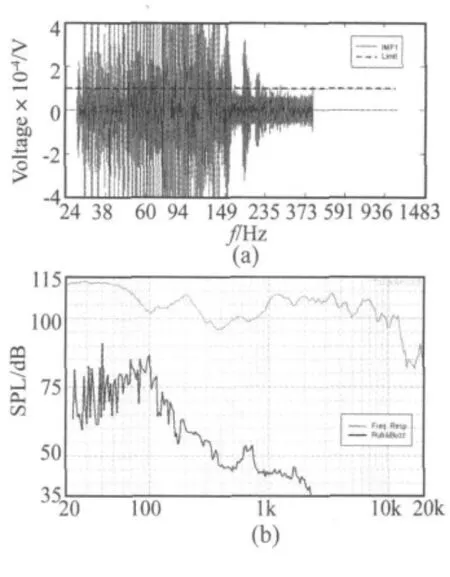
图13 2#（音圈摩擦）样品的（a）IMF1；（b）频响及高阶谐波失真曲线Fig.13（a）IMF1，（b）frequency response and HOD of sample 2#（with coil rubbing defect）.

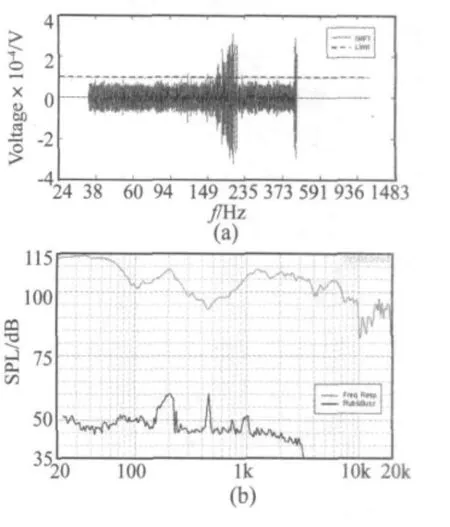
图14 3#（部件摩擦）样品的（a）IMF1；（b）频响及高阶谐波失真曲线Fig.14（a）IMF1，（b）frequency response and HOD of sample#3（with buzzing defect）

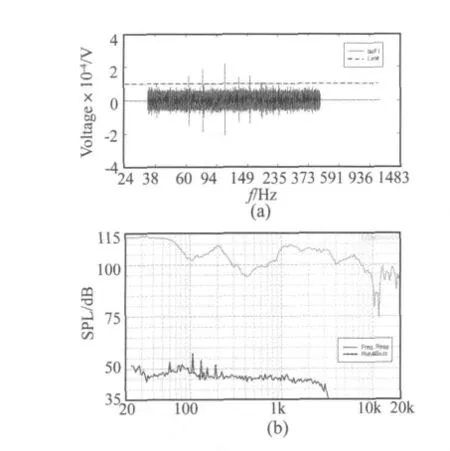
图15 4#（异物碰触）样品的（a）IMF1，（b）频响及高阶谐波失真曲线Fig.15（a）IMF1，（b）frequency response and HOD of sample#4（with loose particles defect）

图13（b）～图15（b）中的高阶谐波失真曲线仅体现了发生异常音故障的强弱和频率，并不包括异常音故障的振动特征。通过EMD法可以取得这些振动特征。将图 13中 IMF1的 20 Hz～30 Hz、图 14中400 Hz～500 Hz及图15中IMF1的90 Hz～120 Hz部分放大，并根据激励信号时间与频率的对应关系将频率坐标转换为时间坐标，得到如图16～图18所示的两个周期内IMF1的局部特征。

观察图15与图18可见，对于异物碰触故障的扬声器，由于碰触的随机性，求得的IMF1中并没有出现周期性特征。而音圈摩擦和部件摩擦故障发生时，振膜的往复运动产生了周期性的异常振动。在图16和图17中可观察到周期性振动的现象，且对于不同的故障IMF1具有不同的包络特征。故可以构建一种异常音分类方法，首先通过IMF的门限确定发生异常音故障的时刻，之后采用支持向量机、神经网络等分类器对局部特征分类。

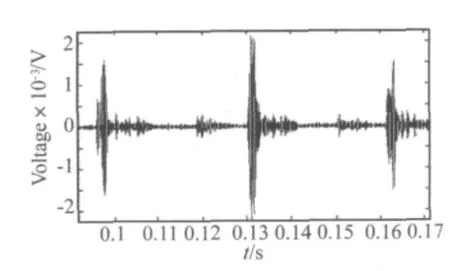
图16 2#样品的IMF1的局部特征Fig.16 Local features of IMF1 of the sample 2#

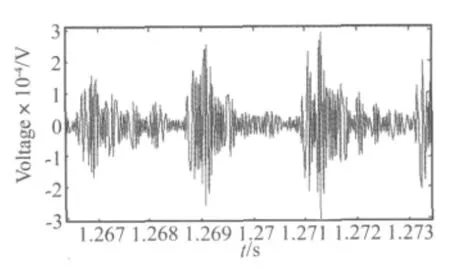
图17 3#样品的IMF1的局部特征Fig.17 Local features of IMF1 of the sample 3#

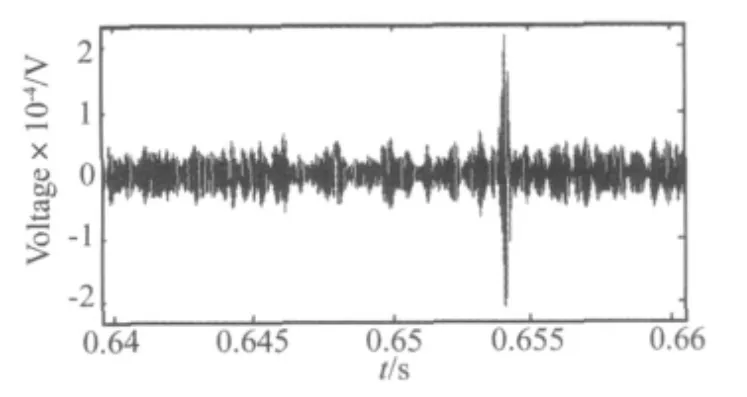
图18 4#样品的IMF1的局部特征Fig.18 Local features of IMF1 of the sample 4#

4 结论

本文提出了一种对扬声器声响应时域处理以检测异常音故障特征的方法，并通过仿真验证和实验验证证明了方法的有效性。在仿真验证中，对模拟异常音的时域特征检测结果表明算法可有效检测三种常见的异常音。在实验验证中，对20只扬声器的声响应进行时域检测，结果表明测量得到的发生异常音故障的频率点与用高阶谐波失真法得到的结果一致。此外，不同的异常音故障对应着不同的IMF的频域及时域特征。这些特征将可能作为扬声器异常音检测和分类的依据。

EMD方法的运算量较大，无法满足在线测试的要求，但目前已出现了EMD的快速算法［18］。另外，实验仅针对一款扬声器的有限个异常音故障样品，不同种类的扬声器是否具有同样的特征还无法确定。且EMD中的混淆现象限制了检测的范围，通过寻找其他激励信号、优化激励信号的参数可能能够令混淆现象发生在检测频率范围之外。未来工作将围绕上述问题展开。

［1］ Groeper G G，Blanchard M A，Brummett T，et al.A reliable method of loudspeaker rub and buzz testing using automated FFT response and distortion techniques.http：//www.aes.org/e-lib/browse.cfm?elib=5555，1991 －10.

［2］Yang Y，Wei J F，Feng H H，et al.A novel technique for detecting and locating loudspeaker defects.http：//www.aes.org/e-lib/browse.cfm?elib=15099，2009 －10.

［3］Thompson S，Pagliaro A，Celmer R.Higher order harmonic signature analysis for loudspeaker defect detection［J］.J.Acoust.Soc.Am.，2003，114（4）2400.

［4］Farina A.Simultaneous measurement of impulse response and distortion with a swept-sine technique.http：//www.aes.org/e-lib/browse.cfm?elib=10211，2000 －2.

［5］杨 益，韦峻峰，温周斌，等.扬声器异常音的快速检测方法及其实验研究［J］.声学学报，2010，35（5）：562 －570.

［6］Leonhard F U.Quality control of electro-acoustic transducers［P］.WO02/25997，2002－03－28.

［7］于德敏，李小明，许增朴.基于时频分析的扬声器异音故障诊断方法［J］.电声技术，2007，31（11）：24 －27.

［8］王旌阳，张 潇，朱俊敏，等.基于时频谱图的脉冲噪声抑制方法［J］.振动与冲击，2010，29（2）：149 －153，192.

［9］朱俊敏，张 潇，王旌阳，等.基于模极大值和尺度理论的音频降噪方法［J］.振动与冲击，2009，28（11）：168 －172.

［10］ Temme S，Brunet P，Keele D B.Practical measurement of loudspeaker distortion using a simplified auditory perceptual model［OL］.http：//www.aes.org/e-lib/browse.cfm?elib=15100，2009－10.

［11］李慧文，邱小军.对扬声器主观音质进行客观音频质量感知评价［J］.电声技术，2010，34（5）：27－31.

［12］ Klippel W.Klippel QC system product brochure［OL］.http：//klippel.de/qc/Klippel_QC_System_brochure.pdf，2010.

［13］ Zwicker E，Fastl H.Psychoacoustics：Facts and models-2nd edition［M］.Germany：Springer，1999.

［14］ Huang E， ShenZ， LongSR. Theempiricalmode decomposition and the hilbert spectrum for non-linear and non-stationary time series analysis［J］.Proc.R.Soc.Lond.A，1998：903 －995.

［15］ Flandrin P，Goncalves P，Rilling G.EMD equivalent filter banks，from interpretation to applications［C］//N Huang，S Shen.Hilbert-huang transform and its applications，London：World ScientificPublishingCo. Pte. Ltd.， 2005，5：57－74.

［16］黄 海.扬声器非线性特性的 Hilbert-Huang变换分析［J］.浙江大学学报（工学版），2005，39（3）：385－391.

［17］ Klippel W，Irrgang S，Seidel U.Loudspeaker testing at the production line.http：//www.aes.org/e-lib/browse.cfm?elib=13649，2006－05.

［18］ Blakely C D.A fast empirical mode decomposition technique for nonstationary nonlinear time series［OL］.http：//www.cscamm.umd.edu/publications/fastEMDcBlakely Final_CS －05 －10.pdf，2005.