地基上下震动时高桥墩的动力屈曲

罗松南，宋君晗，冯 鑫

（湖南大学 机械与运载工程学院工程力学系，长沙 410082）

桥墩是桥梁的重要支撑构件，由于主要承受轴向压力作用，稳定性问题是该类构件要考虑的首要关键问题。我国处于多发的强地震区域，由地震产生的地基运动对于高桥墩的动力稳定至关重要。目前高桥墩的设计大多基于静力屈曲分析［1，2］，与动力屈曲设计存在较大差距。对于动力屈曲问题，有不少学者进行了先期研究。严东晋等［3］对结构冲击屈曲准则提出了讨论；Bakker［4］分析了悬臂圆柱在均布荷载下的剪切屈曲问题；这些研究为研究不同形式的冲击荷载奠定了基础。孙强等［6－8］较系统地研究了竖向谐荷载作用下桩的动力稳定问题。罗松南、李礼［9］研究了三角形冲击载荷和矩形荷载作用下的高桥墩的动力屈曲。这些动力屈曲研究都限于桥面的冲击荷载形式，而对地基运动引起的各种形式的动力屈曲研究甚少。

本文研究高桥墩在地震波引起的地基上下震动时的动力屈曲问题，考虑了大变形的影响，建立了非线性动力学基本方程式。通过数值算例得到了各种不同的地震震级、高桥墩柔度、桥面质量大小的位移响应曲线；给出了高桥墩动力屈曲的全过程；比较了不同柔度、不同桥面质量大小时高桥墩的动力失稳的临界地震级别。可为工程设计提供依据。

1 基本方程式

将高桥墩简化为如图1所示的一端固支另一端简支的等截面受压圆柱，将桥面质量、行驶车辆质量简化为一个质量块，并设其质量为M0（根据文献［12］中给出了公路桥梁构件的自重标准的确定取值），柱长为l，柱的横截面直径为d。当柱体发生变形时，设中面位移为u0（x，t）和w0（x，t），则柱内任一点位移u，w可表示为（不考虑剪切变形的影响）：

应用本构方程和几何方程以及应力与内力之间的关系可得内力与位移的关系为：

其中，E为材料的弹性模量，A为柱体的横截面面积，I为横截面对y轴的惯性矩，ρ为材料的质量密度。α称为非线性因子，当考虑非线性时α=1，当不考虑非线性时α=0。

对整个结构进行受力分析，利用简单的超静定梁求解方法使B点的挠度为零，得出上支座的支座反力的表达式为：

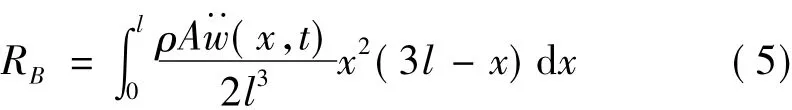
取柱体的任一截面的上半部分进行受力分析，如图2所示，图中的N，Q，M分别为x截面上的轴力，剪力和弯矩。分别考虑x方向力的平衡和绕o'点的力矩平衡有：

将式（3）和式（4）代入式（6）和式（7）可得到用位移表示的非线性动力学的基本方程式时，有：

该问题的边界条件为：

设该问题的初始条件为：

2 求解方法

设基本方程式具有如下形函数解：

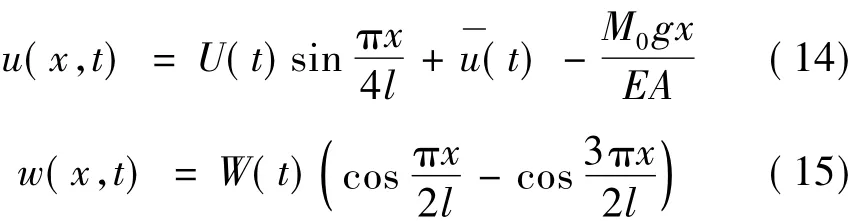
上述形函数满足边界条件式（10）和式（11）。其中，（t）是通过已知地震波加速度波函数积分两次得到的位移函数。

将式（14）至式（15）代入基本方程式（8）至式（9），并应用迦辽金积分，并对其进行整理，得到仅含时间变量的动力控制方程：

其中，a1，a2，a3，a4，b1，b2，b3，b4为伽辽金积分后的有关常数。

由式（16），式（17）通过数值计算可以得到位移U（t），W（t）。

采用四阶龙格－库塔法，计算过程中控制迭代步长将关于时间的微分方程变为代数方程进行数值求解。给定柔度λ，地震加速度a，桥面质量M0等参数来求解u（x，t），w（x，t），绘出高桥墩在地基上下震动时的响应曲线，分析各种参数对响应的影响规律。参照文献［11］中Ellishakoff的观点，采用B－R准则确定高桥墩失稳的临界地震加速度，即高桥墩在地基上下震动时在微小地震加速度增量作用下引起剧烈响应，则认为结构屈曲，对应的值为临界地震加速度。由此给出高桥墩的动力失稳的临界地震加速度和失稳时刻。

3 数值求解

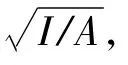
表1 地震震级划分（单位：gal；1 gal==1 cm/s2）Tab.1 dividing of seismic grade（unit：gal；1 gal==1 cm/s2）

图4给出了当M0=2.7×106kg，λ=95（l=33.9 m）时，不同的地震波峰值amax对应的W（t）随时间t的响应曲线。在amax较小的情况下，即为地震震级较小的情况下桥墩发生一定的横向振动，但不会发生动力屈曲，桥墩始终处于稳定状态。随着地震波震级（或加速度峰值）的增大，横向振动幅值明显增大（失稳前大幅横向振动幅值称为Wmax）。通过计算比较可知，当amax=32.72 m/s2，t=9.16 s时，位移有突然剧增的现象出现，挠度趋于无穷大而使高桥墩失稳，因此，amax=32.72 m/s2可视为该高桥墩失稳的临界地震加速度（称为acr）；对应地震级别则为临界震级。即当amax＞acrm/s2时，桥墩会在某一时刻不再振动，挠度不断增大，使桥墩弯曲破环。图4的响应曲线全面描述了地基上下震动时桥墩从稳定到小幅振动再到大幅振动直至失稳的全过程。由图还可看出随着加速度幅值（震级）的增加，失稳发生的时间越来越早，当amax=33.70 m/s2时，在8.1 s失稳。

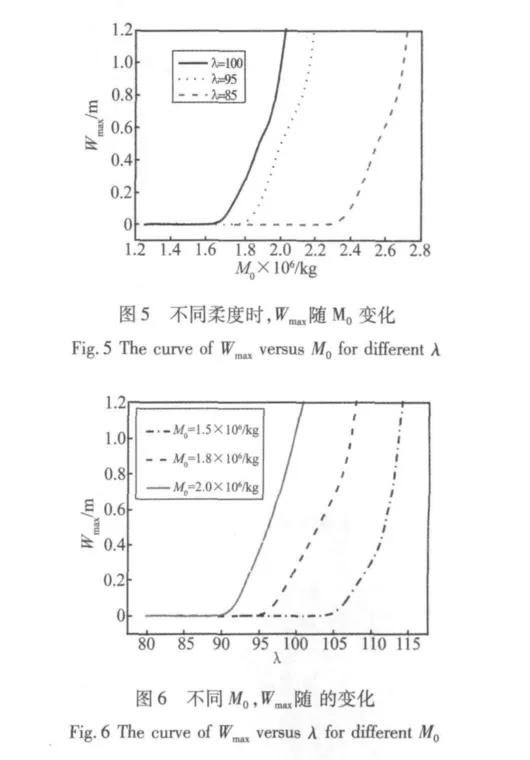
图5给出了当amax=52 m/s2，λ分别为100，95，85时，Wmax随M0的变化曲线。随着M0的增加，Wmax随之增加。当λ=85，M0在 2.4×106kg－2.7×106kg时，高桥墩振动幅度变大，当M0＞2.7×106kg时高桥墩不发生振动，挠度持续增大，使桥墩弯曲破坏。

图6给出了amax=52 m/s2时，M0分别为1.5×106kg、1.8×106kg、2.0×106kg时，Wmax随λ的变化曲线；若M0为1.5×106kg，当λ＜105时，桥墩始终保持稳定状态，位移响应为幅值较小的振动；当105≤λ≤113时桥墩有较大幅值的横向振动；当λ＞113时，位移趋于无穷大，高桥墩会屈曲破坏。

图7给出了当M0=2.4×106kg，λ=98；M0=2.7×106kg，λ=98；M0=2.7×106kg，λ=112时Wmax随地震波的峰值amax的变化曲线。当M0=2.7×106kg，λ=112时，amax＜10 m/s2时，高桥墩只有较小的横向振动，始终处于稳定状态；10 m/s2＜amax＜20 m/s2时，高桥墩有较大幅值的横向振动；amax＞20 m/s2时，高桥墩挠度趋于无穷大而屈曲破坏。amax=20 m/s2可视为高桥墩在此参数下的临界地震加速度，对应的震级为临界地震震级。图中其它曲线具有类似的说明，不再赘述。

图8给出了不同的M0时，临界地震加速度峰值acr随几何参数λ的不同变化曲线。当λ较小时，临界地震加速度随λ的增大而迅速减小；但当λ较大时，临界地震加速度随λ的增加而缓慢减少。

图9给出了不同的λ时，临界地震加速度峰值acr随桥面质量M0的变化曲线。当M0较小时，临界地震加速度随M0的增大而迅速减小；但当M0较大时，临界地震加速度随M0的增大而缓慢减少。

4 结论

本文对受到地基上下震动时混凝土高桥墩的非线性动力屈曲进行了分析，给出了不同的地基上下震动时候的位移响应曲线，描述了高桥墩的动力屈曲路径，分析了各种几何参数和载荷参数对动力屈曲的影响。

（1）不同的简化质量M0，不同的几何参数λ对应的高桥墩的临界加速度acr和失稳时刻不同。当amax＜acr时，高桥墩只会发生较小或较大幅值的横向振动；当amax＞acr时，高桥墩会因挠度趋于无穷大而动力屈曲破坏。

（2）当柔度系数λ越大时，高桥墩失稳的临界地震加速度acr越小，且失稳时刻越早。

（3）当桥面简化质量M0越大时，高桥墩失稳的临界地震加速度acr越小，且失稳时刻越早

（4）根据临界地震加速度对照表1和现在的桥墩稳定设计理论，当地基只有上下震动时，可知在大于8级甚至9级地震时，桥墩才可能会有较大程度的破坏；而对于较低级别地震，不会对桥墩产生破坏。但实际上地震产生的地基运动是复杂的，对于其它的地基运动形式，我们将作进一步的研究。

［1］赵明华，王季柏.基桩计入摩擦力的屈曲分析［J］.岩土工程学报，1996，18（3）：87 －90.

［2］汪 优，赵明华，黄 靓.桥梁基桩屈曲机理及其分析方法［J］.中南公路工程，2005，30（4）：22 －26.

［3］严东晋，宋启根.结构冲击屈曲准则讨论［J］.工程力学，1997，11（4）：18 －28.

［4］Bakker M C M.Shear-flexural buckling of cantilever columns under uniformly distributed load［J］.Journal of Engineering Michanics，2006，132（11）：1160 －1167.

［5］Luo S N，Fu Y M，Cao Z Y.Non-linear vibration of composite beams with an arbitrary delamination［J］.Journal of Sound and Vibration，2004，271：535－545.

［6］孙 强.伸出地面上基桩的动力稳定性研究［J］.岩土工程学报，2003，25（4）：459 －462.

［7］孙 强.竖向动荷载下桩土参数对基桩动力稳定性的影响［J］.工程抗震，2004，3（3）：33－37.

［8］孙 强.竖向谐振荷载下摩擦桩的横向振动性能研究［J］.振动与冲击，2006，25（4）：85 －87.

［9］罗松南，李 礼，周 慧，等.冲击荷载下两端简支高桥墩的动力屈曲［J］.振动与冲击，2009，28（12）：1－3.

［10］罗松南，傅衣铭，曹志远。梁非线性动力分析中剪切力和轴力的相互影响［J］.湖南大学学报，1999，6（3）：9 －12.

［11］王德禹.受静载作用的直杆在轴向冲击荷载下的屈曲［J］.振动与冲击，1997，16（1）：35－37.

［12］郭修武.公路桥梁构件自重标准值的确定［J］.中国公路学报，1997，10（1）：33 －38.

［13］丁秋琴，高艳玲，苗春兰.全球7级以上大地震及中国4级以上地震目录［J］.地震，2009，29（4）：147－170.

［14］郝文化.ANSYS土木工程应用实例［M］.北京：中国水利水电出版社，2005.