考虑损伤双层扁球面网壳的非线性动力学特性

栗 蕾，郝际平，李广慧，黄 义

（1.郑州航空工业管理学院，土木建筑工程学院，郑州 450015；2.西安建筑科技大学 土木工程学院，西安 710055）

网架和网壳结构是近些年来在建筑工程中应用极为广泛的工程结构形式，特别是在大型空间与公共建筑结构中可以说非他莫属了，尤其是网壳结构应用在大空间、大跨度结构中更是屡见不鲜。

众说周知，网架结构通常属于薄壁轻钢结构，它们的变形大都属于大变形范围。在相当的跨度和载荷条件下，网壳结构的刚度较小于其他网格结构并在加载过程中刚度还会削弱，研究表明，在某些情况下倘若不考虑结构的非线性将会导致难以接受的误差，尤其在网壳的稳定性方面，因此用几何非线性分析网壳结构比较合理［1－7］。特别是由于网壳在制作杆件材料不可避免的都带有一定的损伤，因此对于带损伤的网壳的非线性分析的研究实属必要，笔者注意到关于这方面的研究尚不多见。作者正是在这方面做了一些尝试。基于Lematire等效应变损伤理论，计及扁球面网壳各个杆件的损伤影响，应用拟壳法导出了具有损伤的扁球面网壳的动力学非线性控制方程。提出了以中心最大振幅为摄动参数的摄动－变分法的求解方法，对动力非线性控制方程进行了求解，得出了相应的物理量的解析式。据此进行数值分析，得出了相应的特征关系。并用Galerkin方法导出了一个含二次和三次非线性振动微分方程并求解了具有损伤扁球面网壳的的非线性动力学的自由振动方程，给出了准确解。而后利用Melnikov函数法，从理论上给出了考虑损伤的系统发生混沌运动的临界条件，并通过计算机数字仿真证实了考虑损伤的扁球面网壳在非线性强迫振动时存在混沌运动，同时发现损伤使得系统更易发生混沌运动。

1 具有损伤扁球面网壳的非线性动力学控制方程的建立

1.1 具有损伤扁球面网壳的本构方程

首先利用拟板法建立具有损伤壳体的本构方程如下：

式中：［D］为中面刚度系数矩阵，

其中u，v，w为中面上x，y，z方向的位移。

式（2）中：

由式（1）可以得到：

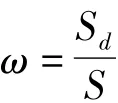
1.2 具有损伤扁球面网壳的非线性动力学控制方程的建立

引入无量纲量如下：

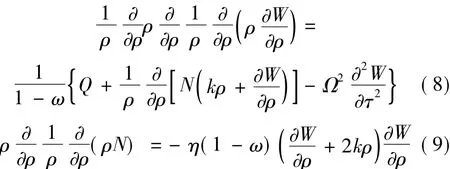
引入周边固定夹紧边界条件：

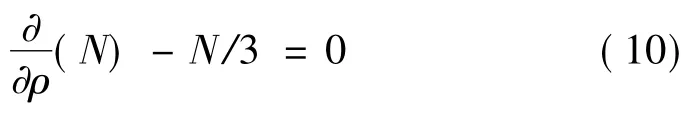
当ρ=0时，

选取系统的初始条件为：

当τ=0 时，W（ρ，τ）=W（ρ，0），

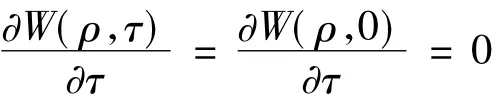
2 基本方程求解

选取扁球面网壳中心最大振幅为摄动参数，利用摄动变分法求解系统非线性振动问题。

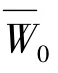
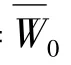
将方程（14）中含有cosτ的项和cos2τ的项分开则：

一次近似边值问题：

边界条件：

当ρ=1时，

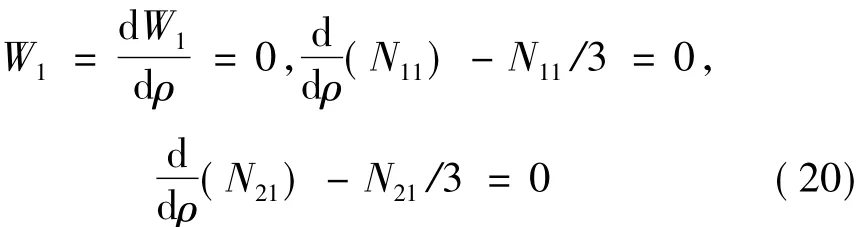
当ρ=0时，

二次近似边值问题：

边界条件：

当ρ=1时，

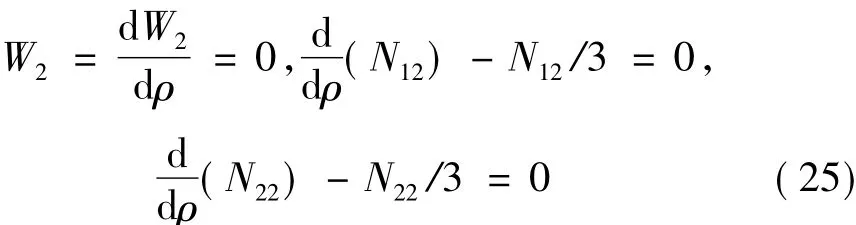
当ρ=0时，

三次近似边值问题：

边界条件：

当ρ=1时，

当ρ=0时，

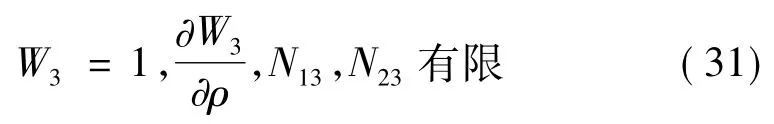
3 对近似边值问题求解

对一次近似边值问题求解得：

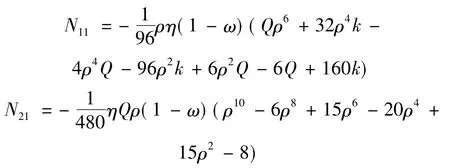
=（1－ω）为具有损伤扁球面网壳的线性固有频率。对二次近似边值问题求解：

对三次近似边值问题求解：

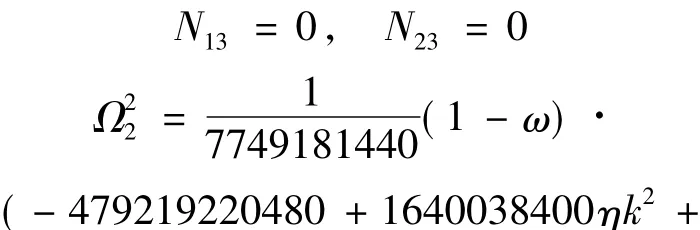
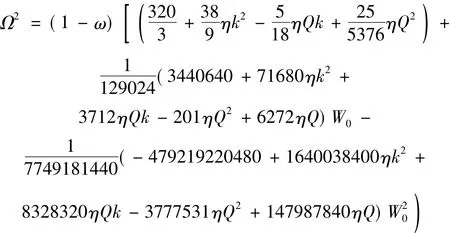
绘出具有损伤扁球面网壳的非线性振动的频率与振幅和频率与载荷之间的特征关系如下：

图1 －W0的特征关系Fig.1 Ω20 － W0 Characteristic relation

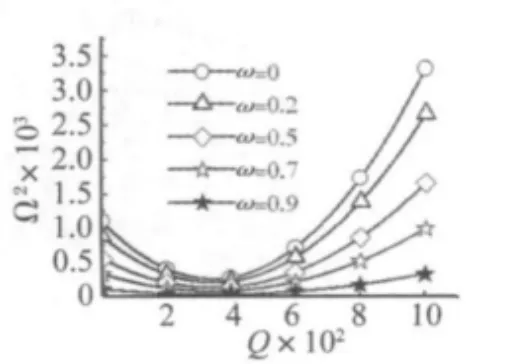
图2 －Q的特征关系Fig.2 Ω20 － Q Characteristic relation

图1，图2给出了不同的ω下的－W0和－Q特征关系曲线，图1中W0=0，对应于考虑损伤扁球面网壳的固有频率。ω=0对应于无损伤理想扁球面网壳的振动频率。显然从图1与图2中可以看出损伤对扁球面网壳的非线性振动特性有明显的影响。损伤使壳体的振动频率降低，这是由于损伤削弱了壳体的抗弯刚度。

4 混沌运动分析

4.1 建立系统的非线性振动微分方程

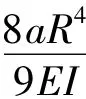
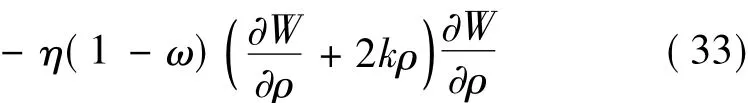
选取固定夹紧边界条件并将其无量钢化为：

当ρ=1时，

当ρ=0时，

选取

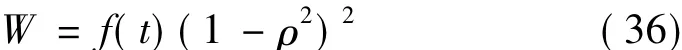
由方程（33）－（36）可以解得：

方程（32）的能量变分方程为：

其中：

把式（36）和式（37）式代入方程（38）用 Galerkin方法得：

由于δf（t）的任意性可以得到：

为了简化公式我们令：

Q=GcosΩ't那么方程（40）可简化为：

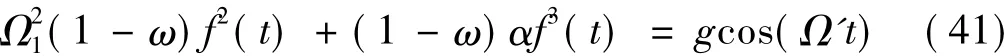
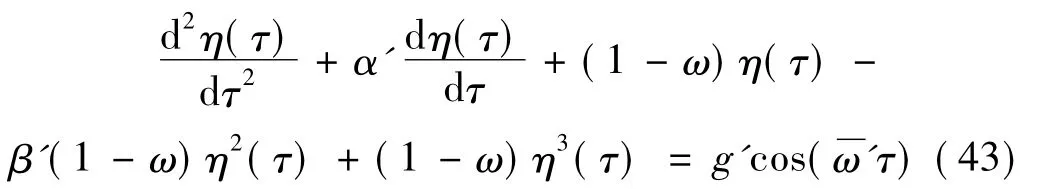
方程（43）为系统的非线性振动微分方程。

4.2 对具有损伤双层扁球面网壳自由振动方程求解

方程（43）的等价方程可写为：

当ε=0时，方程（44）是一未扰动的Hamilton系统，其Hamilton量为：

对于不同的H值，系统将有不同的力学行为。

假设H=0，则系统的Hamilton量为：

求解方程（46）得：

那么：

经验证它们是方程的解。则系统（44）的自由振动方程解为：

4.3 用Melnikov函数分析具有损伤双层扁球面网壳的混沌运动

当ε=0时，方程（44）是一未扰动的Hamilton系统，其Hamilton量为：

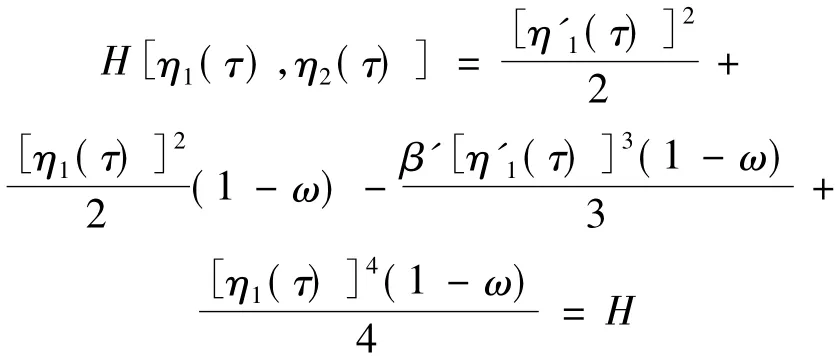
系统沿同宿轨道的Melnikov函数为：

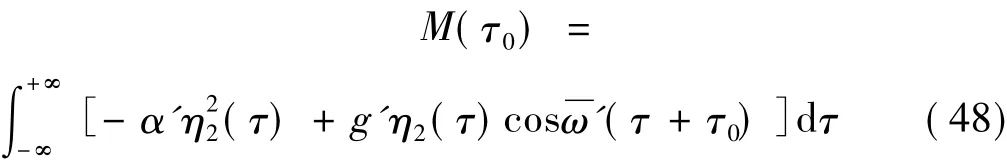
将η2（τ）代入式（48）并经过计算整理后得到：

式中τ0为参考时间，由此式可得，当外激励和阻尼满足：当=1时，

系统含有同宿轨道使相应的Melnikov函数有简单的零点从而系统可能产生Smale马蹄变换下的混沌运动，R（β'）为出现马蹄变换的门槛值。易显，考虑结构杆件损伤的系统更易发生混沌运动。

4.4 数值结果及讨论

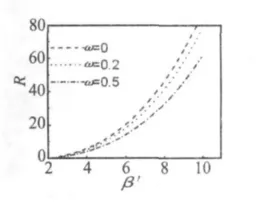
图3 R～β'曲线Fig.3 R ～ β'curve

这里以半径R为40 m，网壳高度h为3 m，失高f为5 m的圆底扁球面网壳为例，材料选用Q235钢材，弹性模量E=2.06 ×106kg/cm2，γ=0.6 t/m3，a=3 m，网壳上、下弦杆面积S1=17.17 cm2，S2=13.08 cm2。由图3可以看出损伤ω及系统频率的变化对扁球面网壳混沌的影响，图中给出了不同损伤下系统可能发生混沌运动的临界值。随着损伤程度的增加可能发生混沌的区域也在增大。随着频率和损伤程度的增大，系统更容易发生混沌运动。为了证实系统发生混沌运动，在Melnikov函数法得到的混沌运动可能的参数域内，借助于计算机模拟，并利用成熟的方法时间历程图，相平面图和Pioncare映射图来证实混沌的存在。计算此网壳系统的无损伤时（ω=0），取α'=0.1，=1，g'=172，β'=2.76，当ω=0.2 时，取α'=0.1，=1，g'=110，β'=2.39。当ω=0.5 时，取α'=0.1，=1，g'=51，β'=1.84。数值模拟结果如图 2，图 3，图 4 所示，其具有明显的混沌特征，时间历程图无周期性，相平面轨迹相互缠绕，既无重叠也无规律，Poincare映射出系统具有复杂的混沌吸引子。因此更进一步证实了混沌的存在，而且很明显现实随着损伤因子的增大混沌的临界载荷越来越小。

5 结论

损伤对扁球面网壳的非线性振动特性有明显的影响，损伤使壳体的振动频率降低，随着损伤的增大振动频率见有较大幅度的降低。另外振动频率随振幅的增大而增大，而且随着损伤的增大表现的尤为明显。因此实际工程应用和设计时应予考虑损伤对结构的影响。

［1］王新志，梁从兴，韩明君，等.扁柱面网壳的非线性动力学行为［J］.应用数学和力学，2007，28（27）：135－140.

［2］王新志，梁从兴，栗 蕾，等.扁锥面单层网壳的非线性动力学特性［J］.动力学与控制学报，2004，12（3）：14 －17.

［3］王新志，梁从兴，丁雪兴，等.单层扁锥面网壳非线性动力稳定性分析［J］.工程力学，2005，22：172 －176.

［4］曹正罡，范 峰，沈世钊.单层球面网壳结构弹塑性稳定性能研究［J］.工程力学，2007，24（5）：17－28.

［5］Li Z X，Shen Z Y.Shaking table tests of two shallow reticulated shells［J］.International journal of solids and structures，2001，38：7875－788481：177－188.

［6］Li Q S，Chen J M.Nonlinear elastoplastic analysis of singlelayer reticulated shells subjected earthquake excitation［J］.Computers and Structures，2003，81：177 －188.

［7］栗 蕾，黄 义.具有初始缺陷的扁球面网壳的混沌运动与控制［J］.振动与冲击，2009，28（6）：6 －7，41.

［8］ Lemaitre J.A course on damage mechanics［M］.Berlin：Springer-Verlag，1996.