新型网壳结构整体稳定性能分析

王晓明

（中国城市建设研究院有限公司兰州分院， 甘肃 兰州 730000）

1 介绍

本文分析的新型网壳结构是在普通单层网壳结构中引入预张力索而成[1]。相对于传统网壳结构，这类新型网壳结构的通透性更好、承载能力更高、材料用量更省。因此，这种新型网壳结构自提出以来已有不少工程应用。除了实际工程应用之外，相应的研究工作也开展不少。这些研究包含基于连续壳体理论对其线性屈曲荷载的估计，极限承载能力分析，缺陷敏感性分析以及试验研究等[2-4]。本文结合线性和非线性屈曲分析对新型网壳结构的整体稳定性能展开研究，重点考察其极限承载能力及影响因素。本文的分析依靠通用有限元软件ANSYS 完成。

2 分析模型

如前所述，本文研究的新型网壳结构是在普通单层网壳的基础上引入预张力索而成。为此，本文同时分析了普通单层网壳和新型单层网壳结构的整体稳定性能。图1 所示为普通单层网壳结构的分析模型。如图1 所示，该单层网壳为一球面网壳，其跨度为80 m，矢高位10 m，网格尺寸为4 m。本文研究的新型网壳结构即是在图1 所示的普通单层网壳中引入斜向拉索而成。

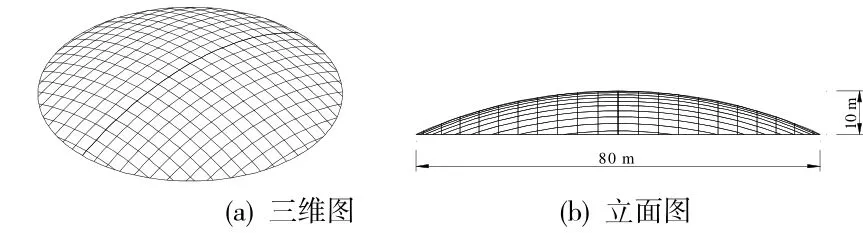
图1 普通网壳结构

本文仅考虑在均布荷载下这类结构的整体稳定性能，且分析时将初始缺陷取为跨度的1/300。网壳所有杆件均采用圆钢管，钢管外径为351 mm，厚度为10 mm。钢管采用Q345 钢，其弹性模量和泊松比分别为2.06x1011Pa 和0.3，拉索弹性模量为1.6x1011Pa。有限元分析时，采用梁单元模拟网壳，而采用只拉单元模拟拉索。

3 线性屈曲分析

图2 所示为普通网壳和新型网壳的屈曲荷载比较。对于传统网壳结构，其最低屈曲荷载约为7.5kN/m2，而新型网壳结构的屈曲荷载大致为13kN/m2。显然，引入拉索之后传统网壳结构的屈曲荷载会得以显著提高，尤其是对于高阶屈曲而言，其屈曲荷载大致会提高至原始承载能力的2 倍左右。

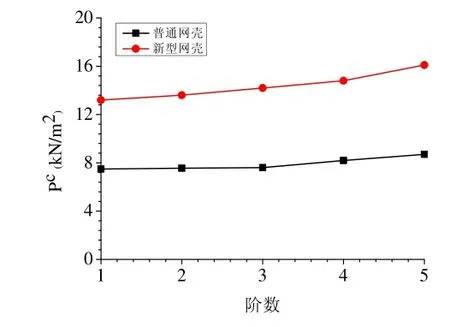
4 参数分析

4.1 拉索面积的影响

拉索面积是影响新型网壳结构整体稳定性能的一大因素，本文通过改变拉索直径反复计算的方式考察其影响。在本文的分析中，拉索面积由116.24 mm2变化到355.98 mm2。图3 所示为不同拉索面积时普通网壳和新型网壳结构的荷载-位移全过程曲线。可以看出，引入预张力索之后，普通单层网壳结构的承载能力得以提高。同时，拉索截面积越大，对应的承载能力越高。

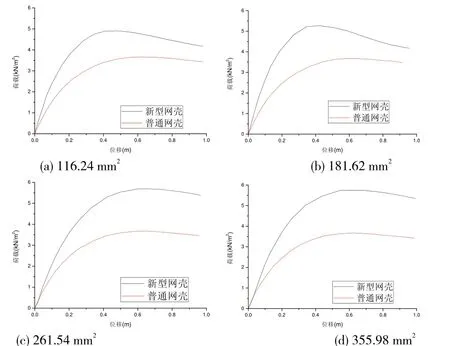
图3 不同拉索面积下网壳结构的荷载-位移全过程曲线

4.2 初始预应力的影响

与上节类似，本节重点考察初始预应力对这类结构稳定性能的影响。在本节的分析中，初始预应力由100 MPa 变化到400 MPa。图4 所示为不同初始预应力下普通网壳结构和新型网壳结构的荷载-位移全过程曲线。可以看出，引入预张力索之后，普通单层网壳结构的承载能力得以提高。同时，初始预应力越大，对应的承载能力越高。

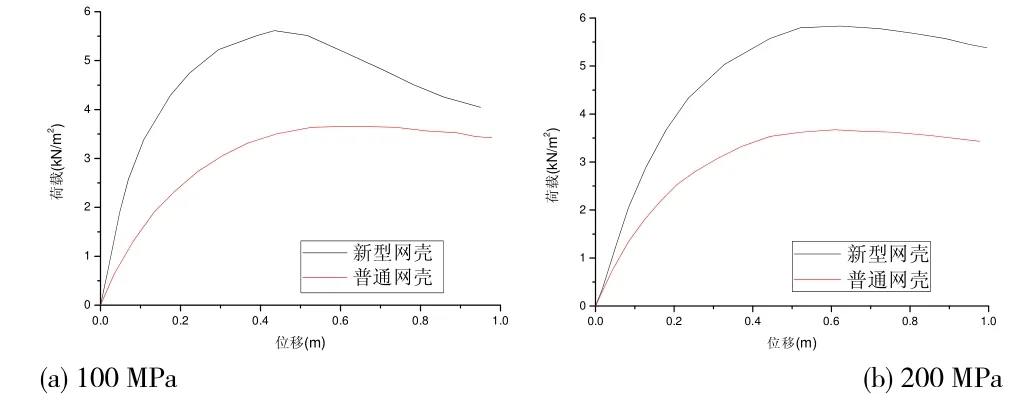
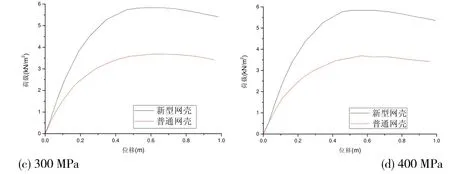
图4 不同初始预应力时网壳结构的荷载-位移全过程曲线

5 结论

本文对一种引入预应力索的新型网壳结构整体稳定性能进行了分析，重点考察了其承载能力。分析表明，这类新型网壳结构的承载能力显著高于普通单层网壳结构。此外，增大拉索截面积和提高初始预应力水平可以显著提升其承载能力。