覆冰四分裂导线除冰过程模拟研究

严 波，陈科全，祖正华，张宏雁，周 松

（1.重庆大学 工程力学系，重庆 400030；2.四川电力试验研究院，成都 610071；3.四川省电力工业调整试验所，成都 610016）

严重覆冰会导致输电线路机械和电气故障事故［1］，特定条件下还会引发舞动等［2－4］。随着“西电东送”和“北电南送”战略的实施，我国电网的覆冰灾害问题更加突出。因此，研究输电线路的除冰技术对冰雪灾害条件下电网的安全运行具有极其重要的意义。

现有的高压输电线除冰的方法较多。其中一类是使电线升温的热力融冰法，如短路电流融冰、高频高压激励融冰、直流电流融冰、潮流调度融冰等。这类方法只适用于覆冰厚度较小的情况，且能耗较大［1］。另一类是电力工人手持木棒、铁扳手或者橡胶棒等敲击覆冰的人工除冰方法，该类方法效率较低且不安全。此外，还有电脉冲除冰［5］、滑轮刮铲法［6］、电磁力撞击除冰［7］、机器人除冰方法［8］和激光除冰［9］等方法也得到了发展，这些方法各有特点。但是，目前尚缺乏一种既经济实用又安全有效的通用除冰方法，这一问题的研究近年备受关注。

机械除冰法有能耗小和价格低廉等特点，具有很好的应用前景。架空导线上覆冰的物理力学性质是研究机械除冰的基础，导线覆冰属于大气冰，目前对其力学特性仍然了解甚少［10］。Druez等［11］测试了大气冰的耐压强度和拉伸强度。Kermani等［12，13］通过冷风洞模拟了大气结冰，测得冰的弯曲强度、等效模量和压缩强度。这些参数可为机械式除冰过程的模拟研究提供参考。

本文针对提出的一种四分裂智能除冰装置的设想，以四分裂覆冰导线为研究对象，采用数值方法模拟四分裂覆冰导线的除冰过程，研究不同除冰装置张开位移大小、冰厚和除冰装置安装个数情况下的除冰效果，讨论智能除冰装置的可行性，同时为该智能除冰装置的设计提供参考。

1 四分裂智能除冰装置的基本原理

四分裂导线智能除冰装置原理如图1所示［14］。该智能除冰装置的工作原理为：环境温度的变化使形状记忆合金1伸长，弹簧2被压缩，此时星形凸轮3顺时针转动，并带动连杆4和棘爪自锁装置6运动。滚动轴承5连接在凸轮3上，可以减少连杆4接触面的磨损。连杆4在滑槽7中作直线运动，同时带动固定连接件9使四分裂导线10之间相互分开。当凸轮3转动45°时，四分裂导线10之间的间距达最大值。此时，棘爪自锁装置6达到棘爪解锁装置8设定的门槛值，同时棘爪解锁装置8中的杠杆机构转动使棘爪自锁装置6解锁，弹簧2突然释放能量，星形凸轮3和连杆4突然返回，从而使导线10突然产生振动，以阻止积冰在导线10上的继续堆积或使导线10上的积冰脱落。

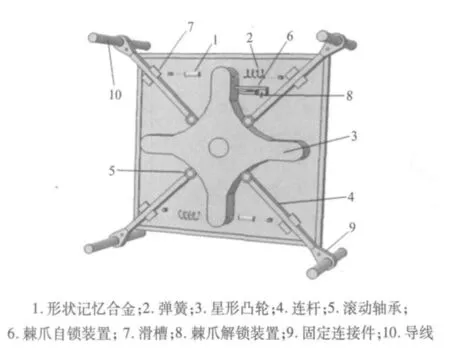
图1 四分裂导线智能除冰装置示意图Fig.1 Schematic diagram of intelligent de-icing equipment of quad-bundled conductor

该智能除冰装置具有经济、安全等特点，而且不需任何附加电源，不需经常维护保养。同时，该智能除冰装置可以兼作间隔棒使用，替代重冰区线路段的部分或所有间隔棒。由于装置的结构和重量与间隔棒差别不大，其重量变化也不大，甚至可以通过优化设计使其比间隔棒更轻，所以不会对导线和杆塔产生大的附加荷载。

2 除冰过程有限元模拟

2.1 覆冰导线有限元模型

建立覆冰导线模型时，假设冰均匀地附着在导线表面。由于导线覆冰过程较缓慢，在此忽略冰中的初始应力。导线和覆冰分别采用相互平行的索单元和管梁单元模拟，平行的两个单元共用节点，如图2所示。在ABAQUS中，模拟导线的索单元可通过将杆单元设置为材料不可压缩实现［15］；覆冰用管梁单元（B31）模拟。

利用文献［16］提出的方法确定导线和覆冰在自重作用下的初始构形，该方法无需迭代计算。为使覆冰导线平衡状态下冰单元中的初始应力足够小，可通过在计算平衡状态的过程中修改覆冰的杨氏模量实现。

图2 导线和覆冰的有限元模拟Fig.2 Finite element simulation of conductor and ice

2.2 智能除冰装置模型

针对图1所示智能除冰装置，建立如图3所示简化模型。该装置总体质量为13.5 kg，假设各杆件的直径为20 mm，可根据其总体质量确定杆件的等效密度。如前所述，智能除冰装置可替代重冰区线路中的部分或所有间隔棒，可按间隔棒的次档距确定智能除冰装置的安装位置［17］。

根据智能除冰装置的工作原理，简化模型模拟的除冰过程如图4所示。当导线开始覆冰时，随着温度的改变，除冰装置的星形凸轮缓慢转动，连杆将四根子导线沿对角方向逐渐向外撑开，当棘爪自锁装置达到极限位置值时突然释放支撑力，连杆带动各子导线瞬间回到初始平衡位置，引起各子导线的振动。在覆冰导线的振动过程中，当覆冰的轴向拉应力超过其破坏强度时，即破坏脱落。

利用ABAQUS中Translator连接单元模拟除冰装置的撑开过程，并对每个连接单元定义局部坐标系，以限制各子导线仅能在除冰装置的对角方向运动。以安装四个除冰装置为例，建立的四分裂有限元模型如图5所示。

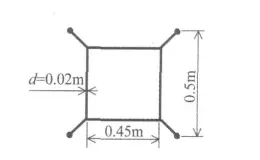
图3 智能除冰装置简化模型Fig.3 Simplified model of intelligent de-icing equipment

2.3 覆冰破坏准则及破坏单元删除模拟

利用ABAQUS中的用户材料子程序VUMAT定义覆冰的本构关系和删除破坏单元。覆冰厚度不大时其剪切变形可以忽略，故覆冰的破坏可采用最大拉应力理论。据文献［18］，覆冰在应变率较高时表现为弹性和脆性失效，当应变率低于10－5s－1时表现为韧性和塑性失效，在此假设覆冰为各向同性弹性体。

为模拟覆冰的破坏过程，用FORTRAN语言编写覆冰的用户材料子程序VUMAT。子程序VUMAT中定义了覆冰的本构关系，并由最大拉应力强度准则实现覆冰破坏单元的判定。子程序VUMAT删除覆冰破坏单元的过程如下：

① 从ABAQUS子程序接口读入上一个增量步结束时的应力张量σold和状态变量stateOld（nblock，nstatev），以及本增量步的应变增量Δε。

② 由广义胡克定律计算试探应力

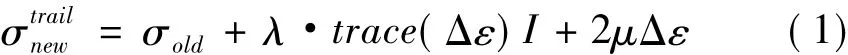
式中：λ和μ为覆冰的拉梅常数，它们与杨氏模量E和泊松比ν间的关系为：

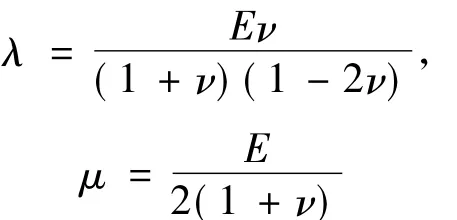
③ 更新应力计算结果

④ 利用最大拉应力强度理论判断覆冰单元是否破坏：当冰单元的拉应力σ11大于抗拉强度σm时，令状态变量stateNew（nblock，nstatev）=0，即删除该覆冰单元。反之，stateNew（nblock，nstatev）=1，即该冰单元保留。

⑤ 更新内能和非弹性耗散能。

⑥ 返回主程序。

2.4 导线和覆冰参数

以A3/S3A－732/92型号导线为分析对象，其相关参数如表1所列。导线的阻尼采用Rayleigh阻尼模型，即阻尼矩阵是质量和刚度矩阵的线性组合：

α和β为与结构和材料有关的常数。根据文献［19］，覆冰导线α取0.1，β取0。

这里以雨凇为研究对象，由于导线覆冰属于大气冰，参考文献［11］，覆冰的相关物理力学参数如表2所列。

表1 A3/S3A－732/92导线参数Tab.1 Parameters of A3/S3A-732/92

表2 覆冰的物理力学参数Tab.2 Mechanical parameters of ice

3 数值模拟结果及分析

以单档四分裂覆冰导线为例，其档距为200 m，无高差，导线安装应力为34.33 MPa。覆冰厚度取10 mm，档内安装4个非均匀布置的除冰装置，模拟智能除冰装置的除冰过程。有限元模型中导线和覆冰均划分为1 000个单元。首先计算分裂导线覆冰后的平衡状态，接着对各子导线与除冰装置的连接点缓慢施加局部位移，以模拟导线覆冰过程中除冰装置星形凸轮转动、连杆向外撑开子导线的过程。当各子导线被撑开到最大位移后，瞬间释放约束，使各子导线在极短时间内回到初始平衡位置，这里设置该时间间隔为0.001 s。

3.1 典型除冰工况数值模拟结果

图6所示为该单档四分裂覆冰导线除冰装置释放局部张开位移后覆冰脱落过程的数值模拟结果。图6（a）为覆冰导线除冰前的平衡状态。当各子导线被撑开到最大张开位移后，释放张开位移，导线开始振动脱冰。如图6（b）所示为释放张开位移后0.005 s时刻导线的状态。可见，此时在除冰装置附近开始脱冰，除冰率为1.08%。图6（c）所示为释放张开位移后0.01 s时刻导线的状态，此时的除冰率达到63.38%。导线最终静止后的除冰率为72.55%。

为讨论该除冰装置的可行性，表3列出了各子导线被张开100 mm时所对应的支撑力大小。此种情况下除冰率接近100%。从表中结果可见，除冰装置与上层两根子导线连接处的支撑力小于与下层两根子导线连接处的支撑力。根据模型的对称性，同层子导线连接处的支撑力应该完全相同，两者的差异源于数值误差。此外，除冰装置1和除冰装置4的支撑力大于除冰装置2和除冰装置3的支撑力，说明除冰装置离分裂导线端部越远，除冰装置达到相应张开位移时需要的支撑力越小。此外，就计算的对象而言，支撑力的大小在150 N～270 N间，表明该除冰装置具有可行性。

图6 覆冰四分裂导线除冰过程数值模拟结果（除冰装置最大张开位移：50 mm）Fig.6 De-icing process of iced quad-bundled conductor（Opening disp：50mm）

表3 除冰装置与各子导线连接点处的支撑力Tab.3 Force between de-icing equipments and sub-conductor

3.2 除冰装置不同张开位移下的除冰率

针对前述模型，模拟除冰装置张开位移分别为10 mm，20 mm，40 mm，50 mm，60 mm，80 mm，100 mm 和200 mm时的除冰过程，研究除冰装置张开位移大小对除冰效果的影响。

图7 除冰装置张开位移对除冰率的影响Fig.7 Relation between de-icing rate and opening displacement of the de-icing equipment

图7所示为除冰率随除冰装置张开位移的变化曲线。可见，随着除冰装置张开位移的增大，除冰率也增大，但除冰率的增加量逐渐减小。当除冰率达到100%后继续增大张开位移已无意义。因此，设计除冰装置时，不宜一味增大张开位移，需要综合考虑各种因素，包括要确保除冰过程中满足各相导线间的电气绝缘要求等。

3.3 不同覆冰厚度下的除冰效果

针对前述模型，模拟研究覆冰厚度分别为5 mm，10 mm，15 mm和20 mm情况下的除冰效果。表4所列为不同覆冰厚度下导线除冰率的对比。可见，同等条件下覆冰厚度越小除冰率越大，即除冰效果越好。显然，应该在导线覆冰较少时即开始除冰，以阻止更大覆冰的形成。

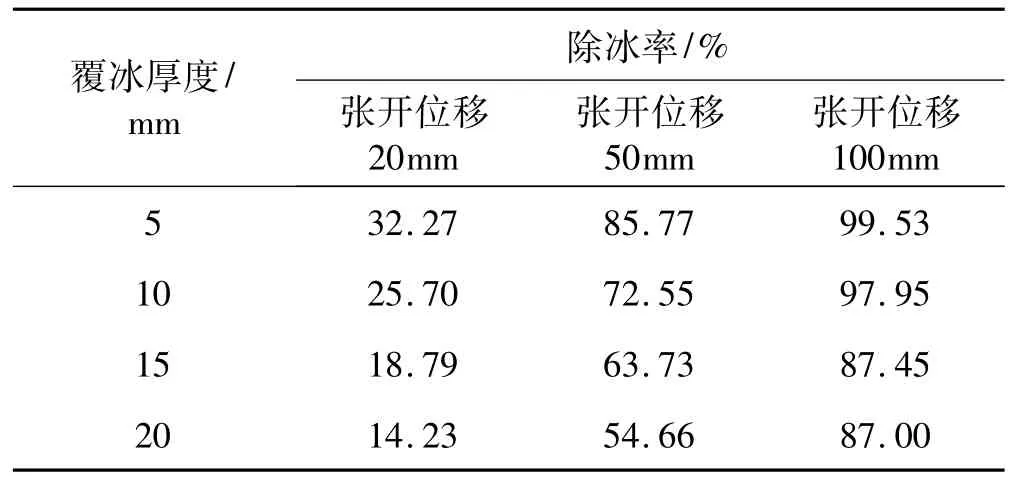
表4 不同覆冰厚度下的除冰效果Tab.4 De-icing rate in different ice thickness

3.4 智能除冰装置个数对除冰率的影响

最后，讨论档内除冰装置安装个数对除冰效果的影响。保持档距200 m，冰厚10 mm不变，模拟研究安装4个，6个和8个除冰装置时导线的除冰过程，考虑了10 mm，50 mm和100 mm三种不同张开位移的情况。

表5所列为安装不同除冰装置个数时的除冰率。可见，除冰装置个数越多，除冰效果越好。现行的输电线路设计规程根据冰区、线路电压等级和档距等规定了档内间隔棒的安装个数和位置，可以根据线路所处地段的覆冰情况和其重要性，用恰当个数智能除冰装置替代间隔棒，以达到理想的除冰效果。

表5 智能除冰装置安装个数对导线除冰效果的影响Tab.5 De-icing rate in different number of de-icing equipment

4 结论

本文针对智能除冰装置的设计思想，利用ABAQUS有限元软件及用户材料子程序VUMAT，实现了除冰过程的数值模拟方法。通过对除冰装置不同张开位移、安装个数以及覆冰厚度等情况下除冰过程的数值模拟研究，得到如下结论：

（1）除冰装置的张开位移越大，除冰率越大，即除冰效果越好。当除冰率达到100%后，继续增加张开位移无意义。

（2）覆冰厚度越小，除冰效果越好。实际应用中应在覆冰厚度较小时及时除冰，以阻止更大厚度的覆冰形成。

（3）同一档距内除冰装置安装的个数越多，除冰效果越好。可根据线路覆冰的严重程度和线路的重要性确定档内除冰装置的安装个数。

［1］申屠刚.电力系统输电线路抗冰除冰技术研究进展综述［J］.机电工程，2008，25（7）：72－75.

［2］严 波，李文蕴，周 松，等.覆冰四分裂导线舞动数值模拟研究［J］.振动与冲击，2010，29（9）：102 －107.

［3］刘小会，严 波，张宏雁，等.分裂导线舞动非线性有限元分析方法［J］.振动与冲击，2010，29（6）：130 －133.

［4］孙珍茂，楼文娟.覆冰输电导线舞动及防舞效果分析［J］.振动与冲击，2010，29（5）：141 －146.

［5］ Robert I，Robert L，et al.An investigation of power line deicing by electro-impulse methods［J］.IEEE Trans on Power Delivery，1989，4（3）：1855 －1861.

［6］ James W H.Ice storm management on an electrical utility system［J］.Proceedings of the 7th IWAIS，Canada，1996：225－230.

［7］Landry M，Beauchemin R，Venne A.De-icing EHV overhead transmission lines using electromagnetic forces generated by moderate short-circuitcurrents［C］//9th International Conference on Transmission and Distribution Construction，Canada，2000：94－100.

［8］杨 暘，高虹亮，孟遂民，等.架空输电线路除冰机器人的结构设计［J］.电力建设，2009，30（3）：93－96.

［9］谷山强，陈家宏，蔡 炜，等.输电线路激光除冰技术试验分析及工程应用设计［J］.高电压技术，2009，35（9）：2243－2249.

［10］Ping F，Farzaneh M，Bouchard G.Two-dimensional modeling of the ice accretion process on transmission line wires and conductors［J］.Cold Regions Science and Technology，2006，46：132－146.

［11］ Druez J，Nguyeh D，Lavoie Y.Mechanical properties of atmospheric ice［J］.Cold Regions Science and Technology，1986，13：67–74.

［12］ Kermani M.Compressive strength and effective modulus of atmospheric ice［J］.Cold Regions Science and Technology，2007，49：195–205.

［13］ Kermani M.Bending strength and effective modulus of atmospheric ice［J］.Cold Regions Science and Technology，2008，53：162－169.

［14］张宏雁，四分裂导线智能除冰装置［P］.中国专利：ZL 2008 2 0223022.4，2009.9.16.

［15］ Hibbitt， Karlsson ＆ Sorensen， Inc. ABAQUS User SubroutinesReference Manual， volumes， version 6.4［Z］，2003.

［16］Yan B，Lin X，Luo W，et al.Numerical study on dynamic swing of suspension insulator string in overhead transmission line under wind load［J］.IEEE Transactions on Power Delivery，2010，25（1）：248 －259.

［17］邵天晓.架空送电线路的电线力学计算［M］.北京：中国电力出版社，2003.354－357.

［18］ Kálmán T，Farzaneh M，McClure G.Numerical analysis of the dynamic effects of shock-load-induced ice shedding on overhead ground wires［J］.Computers and Structures，2007，85（7－8）：375－384.

［19］ Barbieri N，Honorate De Souza Junior O，et al.Dynamic analysis oftransmission line cables，partⅡ damping estimation［J］.Mechanical Systems and Signal Processing，2004，18：659－669.