复合材料层板冲击剪切实验技术研究

彭 刚，冯家臣，刘原栋，王丹勇，王绪财，李树虎

（中国兵器工业集团 第五三研究所，济南 250031）

冲击过载失效和高速冲击侵彻破坏，是兵器防护材料、结构部件在服役中所面对的主要威胁之一。冲击类剪切失效破坏则是材料和部件所要抵御的关键破坏形式，装甲抗侵彻、抗冲击侵彻失稳与破坏，很大程度上是由法向冲击压应力和冲击剪应力的压剪复合加载所造成的。

树脂基纤维增强复合材料（以下简称复合材料）作为轻质、高效抗冲击防护与结构材料，在兵器和航空器上得以广泛应用。复合材料高应变率下抗冲击剪切特性，将会直接决定或影响到复合材料及部件的设计和有效应用，并且复合材料在准静态性能与动态冲击下的破坏失效特点及性能都存在很大不同，因此，准确可靠的完成高应变率冲击剪切性能的试验与表征，获得冲击剪切下复合材料动态性能参数，对复合材料防护结构设计、抗侵彻过载计算模拟和安全评估都是十分重要的。

获得材料动态剪切性能的方法多种多样［1］，如飞片冲击压剪试验技术、Hopkinson扭杆试验技术、Hopkinson压剪冲击试验技术等，但针对非均质各向异性的复合材料，从试样制备、试验技术的可实现性，及工程设计应用的需求分析，Hopkinson压剪冲击试验技术更实用且便于采用。基于一维分离式Hopkinson压杆（SHPB）试验技术，改造建立的分离式冲击剪切杆系统（Split Hopkinson Bar Punch Shear，简称 SHBPS）是进行材料动态剪切性能表征的有效方法。SHBPS的设计和实现也有多种形式：通过试样特殊设计实现的动态剪切［2］、通过输入杆和输出杆端头改造的单槽式或双槽式杆－杆冲剪式［3～5］、输出杆端部改造建立的支座式冲孔动态剪切、输出杆设计成套管的杆－管冲孔式加载剪切［6］，以及杆－管冲孔式加载装置的改进型：杆－管双槽冲剪式加载装置［7］。Harding在利用杆－管式冲剪装置对树脂基玻璃纤维布增强复合材料冲孔剪切试验时发现，冲孔负荷受加载率的影响十分明显，而破坏时的冲孔剪切位移却保持相对稳定；复合材料增强体结构与试样尺寸的匹配对试验结果影响大：细编纤维增强体试样冲孔边缘整齐、负荷～位移曲线可重复，而粗编试样冲剪载荷下破碎，试验结果分散性很大，这说明复合材料冲击剪切试样的尺寸相对于增强结构几何尺寸足够大时，其动态剪切性能才能得到较好的表征。

无论哪种形式冲击剪切试验，如何保证复合材料动态试验结果稳定性，减小分散性，使试验结果更准确且客观反映被测材料的动态剪切性能，并便于实验操作，才是冲击剪切试验技术需改进优化的主要发展方向。

压剪冲击试验具有与防护材料、防护结构的服役状态最相近的破坏作用形式，样品的冲击剪切破坏状态也与弹板作用中破坏模式十分相似。从试样设计和制备的难易程度、冲击剪切技术的可靠性、与实际应用的相似性方面考虑，杆－管结构冲击剪切对平板试样，尤其对层板结构的复合材料试样是合适的，且动态冲击剪切试验及数据处理相对简单。该试验的应变率范围在104/s量级，与实际服役状态的104－105/s是基本吻合的。

1 SHBPS实验装置的改进

1.1 SHBPS实验技术分析

分析基于分离式霍普金森杆的高应变率剪切性能试验的的冲击加载形式，可以发现：利用SHPB的基本要求，以特殊试样设计进行的冲击剪切加载试验，对各向异性的复合材料的动态剪切性能的表征不是一个有效地方法。例如Meyer利用轴向冲击压缩来实现剪切加载的帽形结构试样（图1），通过自剪切的设计来测定材料局部位置的冲击剪切破坏强度，该方法的局限性大，且试样结构复杂制备难度大，对复合材料等各向异性材料则难以实现，并且试样本身的复杂性也使得试验和数据处理比较复杂和困难，杆－杆式冲剪加载（不论是单槽冲剪还是双槽冲剪，图2与杆－管槽口式剪切（图3）都存在以下典型技术问题：有效剪切面积有限、试样尺寸设计受约束，易增大试验结果的分散性；杆（管）端槽型或凸台的结构设计，会导致应力波传播复杂化，干扰杂波的出现增加了数据处理的难度。另外，双槽冲击加载剪切方式，存在的切应力导致输入杆与输出杆（管）的相对转动，在剪应变增大时，试样不再以纯剪形式破坏。上述问题又较难克服或规避。

图1 利用纵向加载产生剪切变形的帽形试样［2］Fig.1 Hat-like specimen for shear leading under axial compression impact［2］

图2 杆－杆型动态剪切装置示意图Fig.2 Schematic of bar-bar type dynamic shear setup

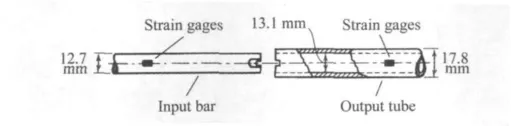
图3 杆－管型双槽动态剪切装置示意图［7］Fig.3 Schematic of bar-tube and double-groove type dynamic shear setup［7］

杆－管冲孔式冲击加载装置，边界约束清晰，是层板复合材料动态剪切性能的一种较好的试验表征形式。首先，一维应力在“杆－管”中传播单一，应力分析简单、明晰，便于数据处理；其次，试样制作简单，试样性能可较好反映材料的性能，并且试验控制技术相对简单，输入杆与输出管的相对轻微转动不影响试验结果，对复合材料的试验有优势；杆－管结构中，输出管代替输出杆，将有利于应力波传播中的横向应力效应的改善［5］。对于杆－管型冲剪试验设计也同样存在一些技术问题：冲击过程输入杆与输出管保持对中困难；受复合材料试样表面平整性、厚度均匀性影响，输入杆与试样接触受力不均，导致输入杆的跳动，同时，试样非均匀性剪切及剪切间隙不均，导致结果分散性大等问题。但这些技术缺陷是可以通过试验系统的改进与优化，并进一步规避或弱化。

复合材料层板非均质各向异性的特点，决定了其垂直于板面不同走向上的抗冲击剪切性能可能不同，而“杆－管”圆孔式冲剪表征的则是复合材料层板的综合冲击剪切能力，测试数据将更趋于稳定。复合材料层板中较大增强体尺寸的特点，则要求冲击剪切区域要足够大，实验数据才能反映材料性能，因此圆孔式冲剪比仅能局部剪切的“槽式”冲剪更有优势。复合材料层板的后加工性远逊色于金属，板面的平整性相对较差，杆系冲剪会造成较大跳动，这也是冲剪实验必需考虑的难题。

综上分析可以发现，杆－管式动态冲击剪切方式，是获得高应变率剪切性能的一种较好的平面冲击加载方式，只要对该实验技术进行适当的改进和优化，克服该试验方式存在的技术缺陷，可成为表征复合材料层板高应变率剪切性能较为理想的实验技术方法。

1.2 SHBPS实验装置的优化与改进

在满足SHPB实验技术基本要求的前提下，针对复合材料层板的材料和试样特点，对杆－管加载进行了如下改进：

（1）为了保证冲击剪切过程中输入杆与输出管的稳定对中，不出现接触受力不均而发生跳动、周向剪切间隙不均匀等问题，且试样便于固定，在杆－管间设计加装了一套“定位对中导向器”装置，示意图如图4所示。输入杆导向口与输出管定位口采取不同公差设计，并保证导向器与输入杆和滑动管间保持滑动配合。试样由试样槽放入，并由槽内塞块塞紧固定。

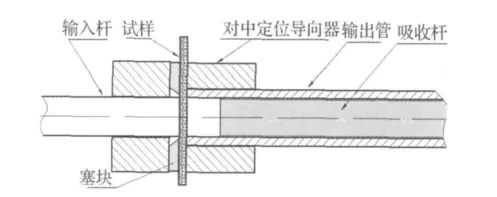
图4 冲剪定位对中导向器示意图Fig.4 Schematic of centring guide apparatus of punch shear

（2）为了保证冲击能量的平稳传递，冲击过程中输入杆总的前进位移量应适当，避免输入杆上的应变计及传输信号线受到损伤，在输出管中放置一根能量吸收杆，以吸收冲击后的剩余动能。吸收杆与输出管要有良好的滑动性，且吸收杆端与试样要保持一定的预留距离。

（3）为了避免冲击过程中应力波传播的衰减和干扰杂波的产生，便于分析计算，使输入杆和输出管的广义波阻抗应保持一致：（Aρc）i=（Aρc）t，因此，若输入杆和输出管采用相同的材料，则它们的横截面积应保持相等Ai=At。

杆－管冲击剪切装置的改进与优化，较好的解决了杆－管对中难、调试难、试样非均匀化剪切，及输入杆因试样端面造成的跳动等问题，且试样也便于夹持固定。冲击过程满足一维应力传播的基本要求。图5为超硬铝制备的定位对中导向器在实验中的应用情况。

图5 定位对中导向器在实验中的应用Fig.5 Application of centring guide apparatus in test

1.3 实验参量的匹配性分析

1.3.1 试样尺寸与冲击杆/管的匹配分析

冲击剪切是压剪复合作用的过程，要实现被测材料达到较理想的纯剪切状态，即实现正压应力到侧剪应力的理想转换，并且试样被剪切破坏前不应发生压缩破坏。因此，入射应力波脉冲，特别是前沿脉冲应能够在试样剪切厚度方向上完成多次往返传播，使剪切厚度方向压应力σ尽量均匀化，同时让被剪切区域受力均匀，反映材料的抗冲剪特性。要实现试样既不被“压坏”，沿厚度方向局部区域应力均匀的目的，需对被测试样进行约束设计，按应力波试样内2－3次往返可满足均匀化要求［6］，则有：

式中：h为试样厚度，mm；cL为试样厚度方向波速（m/s）；tcr为入射应力波前沿时间宽度（μs）；n为入射应力波前沿在试样厚度上的往返次数，n=2，3。

对高强度钢质冲击杆，冲击应力波的前沿脉冲宽度一般在（5 μs～6 μs左右，对入射脉冲可适当整形，增大脉冲前沿宽度，则对试验结果更为有利。

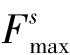
即：

在通常情况下τ≤σ，若适当放大剪应力估值，使τ=σ，则可认为d/h≥4，是确保试样冲孔剪切破坏前不会压缩破坏的条件之一。事实上，最好应是试样被剪切时不会发生压缩塑性形变。对Φ14.5 mm的输入杆，复合材料试样的厚度一般取3 mm～4 mm左右。对增强体尺寸较小的复合材料d/h可以取小些，而大尺寸增强体的复合材料，d/h就需取大一些，这样实验结果一致性更好。

1.3.2 剪切间隙的分析

输入杆与输出管间的预置剪切间隙是决定试样有效剪切破坏的另一关键要素。预置剪切间隙过小，会导致压剪复合作用中压缩破坏权重的增大，并且试验中输入杆与输出管的对中操作难度大，容易发生杆与管端部碰撞和试验结果分散等问题。预置剪切间隙过大，则容易造成冲击过程中材料因发生弯曲而失效。预置剪切的间隙，是复合材料冲击剪切实验设计中的重要一环，直接影响到试验动态剪切破坏性能的测定。为此，我们采用数值分析方法，通过冲击剪切过程中输入杆和输出管之间间隙参数的分析研究，以寻求针对复合材料试样恰当的预置间隙，使预置间隙成为材料的绝热剪切破坏带区域。

数值分析采用了ANSYS有限元计算程序，以铺层顺序为［0/90］的3 mm厚热固复合材料层合板为模拟分析参照样板。输入杆外径d=14.5 mm，弹性模量E=210 GPa，泊松比ν=0.3。a为输入杆与输出管之间间隙（图6）。

冲压有限元模型如图7所示，对输入杆与层合板接触区域进行局部网络细分，如图8所示。

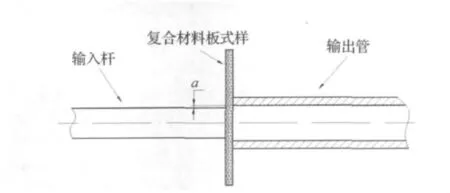
图6 冲头和套管结构简图Fig.6 Schematic diagram of plunger and tube

图7 有限元模型Fig.7 Finite element model

图8 局部网格细分Fig.8 Subdivison of local mesh

数值模拟分析显示，复合材料层合板在动态剪切过程中，纤维基体剪切破坏单元数量D随冲头和输出管之间间隙a的变化规律如图9所示，从拟合曲线可以看出，间隙为0.1 mm时，层合板中剪切破坏数量最多，冲击剪切性能最好。考虑到实际加工误差，以及输入杆与输出管动态实验的实际配合状态，建议冲头和输出管之间间隙可预置为（0.2 ～0.3）mm ±0.05 mm。图10为冲头与模具之间间隙为0.1mm时，复合材料层合板典型铺层损伤情况。

图9 剪切破坏单元D的数量随间隙a的变化曲线Fig.9 Relationship between the number of shear failure units（D）and clearance size（a）

2 复合材料层板的冲剪试验

为了验证装置改进优化后冲剪试验的可靠性，选取了应变率效应不敏感的1mm厚LY12cz材料作为验证试样，分别在优化后的SHBPS系统和准静态试验机上进行了动态和静态压剪试验，两组试验数据吻合很好，三个试样的强度均值分别为τd=275.7 MPa，τs=279.5 MPa。

由试验结果可以看到，相同冲击速度下各试样得到剪应力～位移数据重复性较好。冲剪后的试样剪切区整齐，面内剪切区域均匀，剪下的部分未发生压缩破坏现象，厚度未发生变化，说明未发生压缩塑性形变。

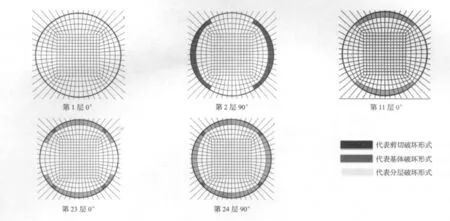
图10 0.1 mm间隙时复合材料层合板的损伤状态Fig.10 the failure of composite laminates for 0.1 mm clearance

实验中，输入杆和输出管移动合理，应变计及信号线完好。残余能量基本由预置吸收杆吸收，实验后吸收杆飞入缓冲器。

所测复合材料的剪切强度受加载率（应变率）影响明显，成正比发展，说明应变率对复合材料抗剪力学性能的影响不可忽视。但数据显示，最大强度下的位移变化并不大。

3 结束语

（1）基于一维Hopkinson杆的“杆－管”冲剪技术是适合复合材料层板高应变率剪切力学性能表征的实验方法，实用可靠，便于操控。

（2）冲剪定位对中导向器的设计使用，在不影响一维应力波传播的条件下，解决了冲剪过程中输入杆和输出管间的抖动、难以同轴对中、试样定位，及实验技术导致的结果分散性大等问题。

（3）要获得良好、可靠的复合材料动态剪切力学性能数据，需考虑“杆－样－管”间实现动态剪切的匹配关系，按照各自尺寸约束条件来设计冲击剪切试验。

（4）根据数值模拟结果，同时考虑试验的对中调试技术要求，以及材料试验面的尺寸公差，对2 mm～4 mm均厚复合材料板冲击剪切间隙取0.2 mm～0.3 mm较为合适。

［1］崔云霄，卢芳云，林玉亮，等.Hopkinson杆动态剪切实验技术综述［C］.第四届全国爆炸力学实验技术学术会议论文集，福州，2006：1 －10.

［2］ Meyer L W，Manwring S，Murr L E，et al.Critical Adiabatic Shear Strength of Low Alloyed Steel Under Compressive Loading，Metallurgical Applications of Shock-Wave and High-Strain-Rate Phenomena［M］.Meyer M.A.Editors，Dekker New York，1986：657－674.

［3］ Hosur M V，Waliul S M，Islam U K，et al.Experimental studies on the punch shear characterization of satin weave graphite/epoxy composites at room and elevated temperatures，Materials Science and Engineering，A368（2004）269－279.

［4］ Dowling A R，Harding J，Campbell J D.The Dynamic Punching of Metals［J］.J.Inst.Metals，1970，98：215 － 224.

［5］ Werner S M，Dharan C K H.The dynamic response of graphite fiber-Epoxy laminates at high shear strain rates［J］.Journal of Composite Materials，1986：365 －374.

［6］ Harding J.Mechanical properties at high rates of strain［C］//Proc.2nd Conf.on the Mechanical Properties at High Rates of Strain Held in Oxford，1979：28－30.

［7］ Harding J，Huddart J.The use of the double-notch shear test in determining the mechanical properties of uranium at very high rates of strain［C］，Proc.2nd International Conf.Mechanical properties at high rates，J.Harding，Editor.，The Institute of Physics，London，1979：49 －61.

［8］宋顺成，田时雨.HOPKINSON冲击拉杆的改进及应用［J］.爆炸与冲击，1992，12（1）：62 －67.

［9］胡时胜.霍普金森压杆技术［J］.兵器材料科学与工程，1991，（11）：40－47.