基于BP神经网络对学生学习专业课程效果的评价

严朝宁

（陕西国防工业职业技术学院机械工程学院 710302）

随着我国高等教育的迅猛发展，学校对办学质量倍加重视。学习效果作为检验学生掌握知识的一个因素也被更加关注，它反应出学生对知识的掌握程度以及教师教学成果和管理的优劣。当然，有许多因素同时影响着教学效果，并且各自占有的影响比重是不同的。因此，我们在评估度量学生学习效果时，很难用数学解析表达式来对其进行表示，显然，这是一个典型的非线性的几何问题［1］。目前，还没有一个公认的、理想的学习效果评价体系。因此，寻找一个简单、优化、客观的学习效果评价方法是相当必要的。从现有的研究状况来看，学习效果评价主要集中在两个方面，一方面是对其体系中内容的研究，另一方面是在对体系中每项指标给定后，怎样评定学习效果等级方法的研究。

1 学习效果评价体系

1.1 学习效果评价内容

我们知道，学生的学习和其自身的发展是一个不断进取的过程，并且学生学习和其成长环境不同。所以将评价指标置于学生学习过程中，从过程管理的层面分析，多因素相互作用和多环节综合体现于整个教学过程，因此，若要对不同学科分类、不同性质的课程、不同的学习环节、不同的学习对象的学习效果进行对比，将会非常困难。基于以上原因，必须要从最能直接反映学习效果并有共性的基本因素等方面去设计评价体系，这样才具有一定的实际可操作性。以下几类要素常应用于现有的学习效果评价体系中。

（1）学习态度：学习是否认真投入，预习是否及时，作业完成是否认真。

（2）学习内容：内容难易度是否得当，与基础知识联系是否紧密，所用到的交叉知识是否多。

（3）学习能力：学生的基础是否好，理解能力、查阅资料能力、动手能力、理论联系实际的能力、融会贯通能力。

（4）学习方法：是否依据自己特长、灵活选用方法，是否注重启发、注重能力，是否注重与请教老师、学生交流、互动。

（5）学习目的：是以掌握自己特长、或是以应付老师、家长、还有考试为目的。

1.2 学习效果评价方法

学习效果评价体系中的各个度量指标一但确定，下一环节的任务就是给出一套合适的方法，处理和分析来自评价体系中的数据。

现有的评价方法有：（1）采用传统的学习效果评价方法，其结果由两方面因素决定：一个是打分制（给评价指标的打分），一个是等级制（不同的评价指标处于不同的等级）。（2）模糊综合评价法，该方法运用模糊数学的理论和方法，对评价主体进行分析评价，最终取得对学习效果的综合评价［2］。

显然，上述两种数据处理方法都无法避免人的主观因素对评价结果的直接影响，使得评价结果一定程度上偏离了客观实际。当然，我们并不否定以上方法在提高教学质量水平、促进学会生学习方面还是发挥了一定的积极作用。要实现对教学效果的客观评价、并且方法具有实际可操作性，仍有待进一步分析探讨。

人工神经网络作为一种新技术，凭借自身非线性映射和学习分类，以及实时优化等作为模式识别，在各类评价问题中得到了广泛应用，为我们研究非线性分类等问题创造了一种全新的思路。为了克服人为因素对评价结果的主观影响，以及为了建立全面合理的综合评价指标体系，本文将人工神经网络引入学习效果评价体系中。基于上述特点，我们建立了一个评价体系BP网络模型，用于评价一门课程的学习效果。该模型具有自组织、自学习功能，通过对网络进行训练，可以对学习效果做出等级评价。

2 BP神经网络评价模型

2.1 BP神经网络的原理

BP（back Propagation）神经网络即前向多层神经网络。标准的BP神经网络由输入层、隐含层及输出层三层神经元构成，该网络模型具有以下几个主要特征：相邻两层神经元之间有连接；各层内神经元之间没有任何连接；各层神经元之间没有反馈连接，并且输入与输出之间表现出极强的非线性映射关系。假定输入层数为n，输出层数为m，那么BP网络便是一个从n维欧氏空间到m维欧氏空间的映射。基于以上原理，我们可以把学习效果评价体系中的各评价指标特性值进行归一化处理，把它作为BP网络模型的输入，把评价结果作为BP网络模型的输出，在可能的前提下，用大量的样本训练这个网络，以便最终得到评价专家对指标重要性判断的一致性倾向，这样BP网络模型的内部结构便显示出网络经过自适应学习所得到的根据需要评价的学习效果各指标属性值。训练好的BP网络模型就可得到对学习效果的评价结果，专家的经验、知识、主观判断及其对指标重要性的倾向可以再次重现，有效实现定性与定量的结合，确保评价结果的真实客观［3－5］。

2.2 评价指标体系的建立

学习效果的评价是通过学习过程中的一些因素来建立评价因素，从而得出正确的评价等级［6］。可以确立以下指标体系。如图1所示。

2.3 确定评价等级

评价等级档次集：b＝｛b1，b2，b3，…，bm｝.学习效果评价等级集合可以划分为：B＝（b1，b2，b3，b4，b5）＝｛优秀，良好，中等，及格，不及格｝。

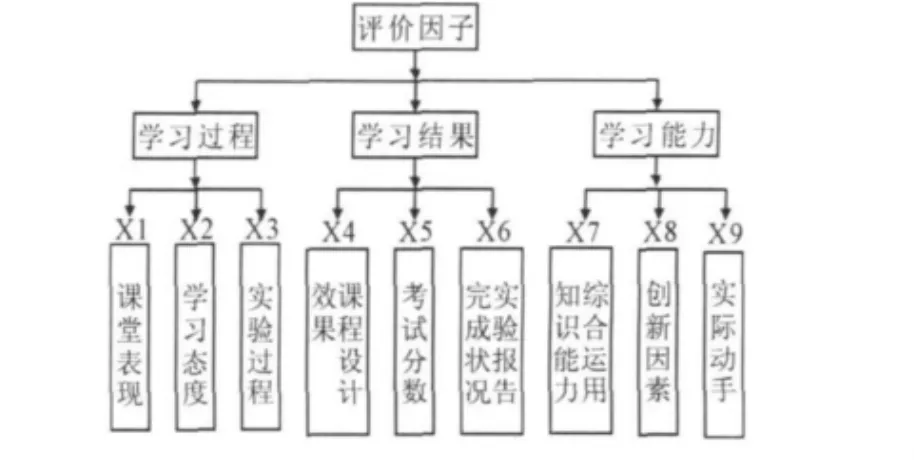
图1 学习效果的评价因子

2.4 BP网络评价模型的确立

网络模型结构选择的好坏，直接影响到网络训练次数的多少及网络学习的精度，因此十分重要。

（1）正确给定输入层神经元个数。由指标体系知，共有9个主要指标影响学习效果，因此假定输入层个数n＝9。

（2）正确给定输出层神经元个数。评价结果是网络的输出，因此假定输出层个数m＝1。

（3）正确给定网络隐含层个数。神经网络学习速度快慢与，隐含层个数多少有直接关系，根据Kosmogorov定理，如果网络结构合理且权值条件恰当，理想的结构模型是3层BP网络，因为其可以趋近任意的连续函数，故结构相对简单的3层BP网络是我们最终的选择。

（4）正确给定隐含层神经元个数。通常我们是根据网络收敛性能的好坏来确定隐含层神经元个数的。通过对大量网络模型结构的分析研究，得到经验公式如下：

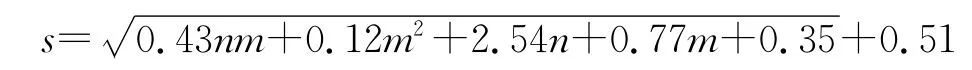
根据经验公式，得隐含层神经元个数为6。

（5）合理确定神经元转换函数。一般均采用S型函数作为BP神经网络神经元转换函数，其具体函数形式为：

（6）合理确定模型结构。综上所述，确定如图2为BP网络模型结构。

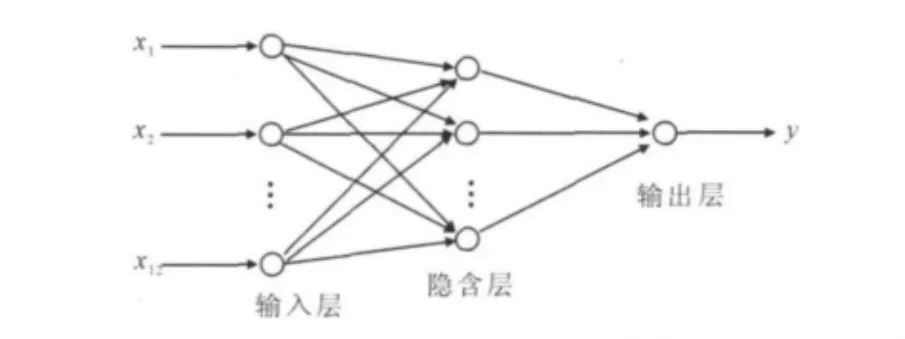
图2 BP神经网络模型结构

3 课程学习效果评价神经网络模型的实现

建立三层BP神经网络，选用高性能的数值计算可视化软件MATLAP，隐含层神经元6个，输出层神经元1个，输入层神经元9个，学习次数为1000次，迭代次数为500次。初始步长选取0.9，M取值400，动量系数为0.9，允许误差0.001。为简化网络结构可以只用3个输出节点表示5种状态类别：b1优秀表示为（0，0，1）；b2良好表示为（0，1，0）；b3中等表示为（0，1，1），b4及格表示为（1，0，0）；b5不及格表示为（1，0，1）。

选取12对样本数据，数据已由百分制做了归一化处理，如下表1所示，测试结果与专家评价结果比较。通过对测前10组数据采用MATLAP神经网络工具箱学习训练网络，我们最终获取并建立了神经网络评价模型。训练步骤及误差如图3所示。由图3可知，当训练步骤达到800步时，误差即小于0.001，为0.00077。通过对后两组测试数据的进行验证发现，预测结果与专家评价结果一致，表明网络训练结果很准确。如表2所示。

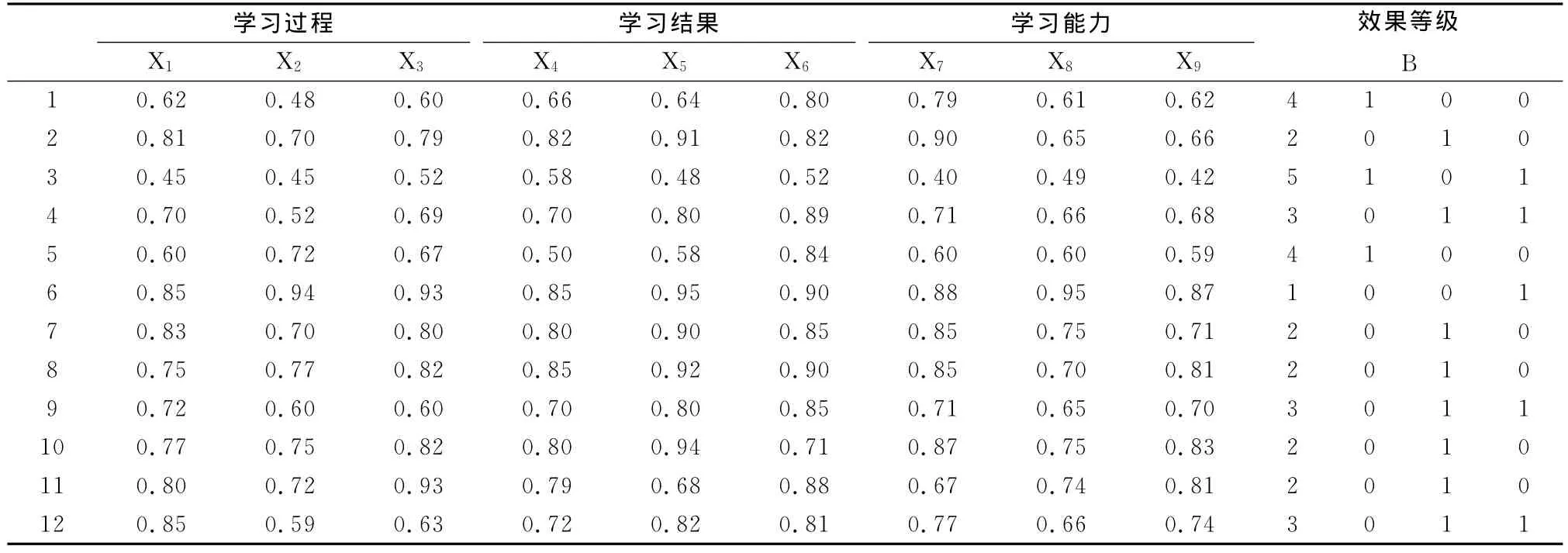
表1 学校效果打分及专家评价样本

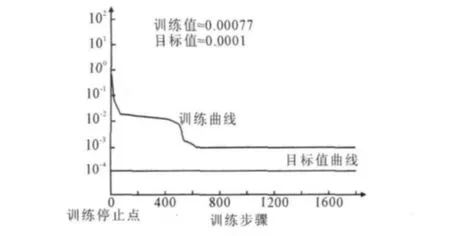
图3 训练步骤及误差

表2 学习效果评价输出值

4 结束语

本文采用BP神经网络的对学生学习一门专业课的效果进行评价，其中选用某一门专业课程的12组打分作为系统样本，其中10组作为训练样本，2组打分作为检验样本，通过Matlab软件，完成了网络的实例训练和验证，结果表明，评价结果与专家评价一致，因此，BP神经网络模型可以较准确的对学生学习某门课程的效果进行有效的评价，是一个简单、公正、客观的评价方法。

［1］ 丁邦俊：高职毕业设计环节的重要性及创新方略［J］.无锡商业职业技术学院学报，2007.2，No7（1）.

［2］ 张金梅，员世芬，谢克明.人工神经网络在教学质量评价体系中的应用［J］.太原理工大学报，2005，vol.36，No.1.

［3］ 唐幼纯，胡建鹏.神经网络在旅游可持续发展能力评价中的应用［J］.计算机工程与设计，2008，29（18）：4815－4818.

［4］ 韩立群.人工神经网络理论、设计及应用［M］.北京：化学工业出版社，1996.

［5］ 周志华，曹存根.神经网络及应用［M］.北京清华大学出版社，2004.

［6］ 盛承发.科技评估的效率原理与模型探讨［J］.科研管理，2003，24（1）：40－42.