利用蒙特卡罗方法设计医用加速器均整器

潘夫兴， 罗文芸， 周诗情， 董晓庆， 王传珊，陈 捷， 吴国华， 查元梓， 蒋马伟

(1.上海大学射线应用研究所，上海200444;2.上海交通大学医学院附属新华医院放疗科，上海200092)

目前，医用直线加速器通常采用能量在4～20 MeV的X射线作为照射源，并且电子束打靶产生的X射线束剂量分布不均匀，需要使用均整器进行修正，使其在治疗处得到35～40 cm大小且满足一定平坦度和对称性要求的剂量分布，才可以用于临床治疗［1-2］.由于各种能量的X射线在透过不同物质时的衰减程度不同，因此，发生光电效应、康普顿效应或电子对效应等相互作用的几率不同.均整器的材料选取以及几何参数的设置已成为了一个值得研究的问题［1，3］.

蒙特卡罗(Monte Carlo)方法非常适合于解决物质中粒子的输运问题，可以用来模拟粒子与物质的相互作用，被称作“理论上的实验”.由于 Monte Carlo方法具有解析方法无法比拟的优点，因而在核科学、统计物理、分子动力学、医学等自然科学领域得到了广泛的应用［4-6］.BEAMnrc是一种通用的Monte Carlo程序包，可用来模拟光子、电子等粒子输运问题［7-8］.BEAMnrc全面考虑了电子、光子在通过物质时发生的各种相互作用，通过对大量粒子历史的追踪记录，得到治疗野平面的相空间数据.BEAMdp和DOSXYZnrc程序可以用来分析相空间数据，得到粒子在治疗野平面上的能量注量、能谱分布角分布以及模体中的离轴剂量分布、离轴比(offaxial ratio，OAR)、百分深度剂量(percentage depth dose，PDD)分布等信息［9-12］.

张洁熹等［3］利用 Monte Carlo程序 BEAM对XHA9医用加速器治疗模式进行了模拟，计算了水模中的PDD分布曲线，分析了各部件产生的电子对治疗电子束的贡献，确定了限光筒产生的大量低能电子是导致出现标称能量低、表面剂量偏高的主要原因.通过修改限光筒、散射箔等部件，分步优化了治疗头结构.Sawkey等［13］将测量所得的西门子加速器机头参数作为模拟参数输入，利用 EGSnrc/ BEAMnrc程序对6MV和18MV医用加速器进行了模拟，并将模拟计算得到的X射线剂量分布曲线与实验测量得到的剂量分布曲线进行了对比，二者的一致性非常好，说明Monte Carlo模拟计算结果非常准确，可将这种方法应用于临床.

本研究利用BEAMnrc程序构建了加速器治疗头模型，采用尝试错误法设计了X射线均整器.首先对几种单一材料均整器下的射野剂量分布进行了模拟计算，通过分析各种材料对X射线衰减程度的特征，选择了两种金属作为均整器材料.反复调整几何参数进行计算，最终使得X射线在通过所设计的均整器后射野剂量分布均匀，满足了国家标准规定的均整度要求.此外，本研究还讨论了X射线剂量利用率、粒子角分布及带电粒子污染问题.

1 模型与方法

1.1 治疗头参数设置

本研究所建立的加速器治疗头模型如图1所示.采用16 MeV电子束打靶产生的X射线作为辐照源，电子束半径为0.001 cm，垂直入射打靶，靶几何形状为长方体，长和宽均为1.6 cm，厚为1 cm，分3层，各层厚度由上而下依次为 0.16，0.64和0.20 cm，材料依次为金、水和不锈钢.模拟粒子数目为107个，取标称源皮距(source skin distance，SSD)为100 cm，射野为10 cm×10 cm光子束照射野.初级准直器、次级准直器等部件按厂家给定参数设置.受治疗头内部空间条件的限制，均整器的几何外形给定为底面半径为3.0 cm，高为3.2 cm的圆锥(见图2)，其他模拟参数按程序默认值设置，均整器的材料及其几何参数需要多次模拟后确定.

图1 加速器治疗头模型Fig.1 Model of medical linear accelerator head

1.2 均整器的设计

图3为模拟计算的流程图.治疗头的主要参数设定如1.1节所述，均整器参数的确定采取尝试错误法，即预先设定其材料和几何参数，在一次计算完成后对得到的数据进行分析，然后修改均整器的材料及几何参数再次计算.重复上述步骤，直至得到满意的结果为止.主要步骤如下：①选取铅作为均整器材料，其他参数如1.1节所述，进行仿真模拟;②分别选取铝、铜、钨作为均整器材料，其余参数同步骤①，分3次进行计算;③ 分析以上两步计算结果，设计复合材料均整器，几何外形如图4所示.采用两锥或多锥嵌套结构，即在上述固定外形的圆锥形均整器内部依次插入一个或多个小圆锥，内外圆锥的材料参数根据各材料对X射线的衰减程度和均整程度的不同而定.通过反复调整内部圆锥的锥度及底面半径，调节各材料的相对厚度，直到X射线剂量分布均匀且符合相关技术标准为止.

图2 沿Z轴方向的单一材料均整器剖面图Fig.2 Profile chart along Z direction of single-material flattening filter

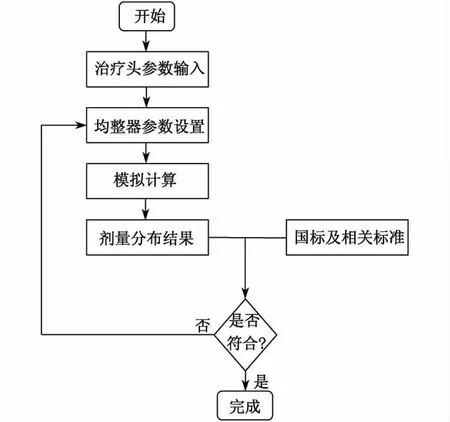
图3 模拟计算流程图Fig.3 Flow chart of simulation

图4 沿Z轴方向的复合材料均整器剖面图Fig.4 Profile chart along Z direction of multi-material flattening filter

2 结果及分析

2.1 离轴剂量分布与离轴比

离轴剂量分布与离轴比是衡量射野平坦度和对称性好坏的重要标准［14］.由图1可以看出，治疗头关于X，Y轴轮换对称，故只计算了X轴方向的离轴比及离轴剂量分布.图5为单一材料均整器对应的离轴比曲线.可以看出，低原子序数的铜、铝均整器对X射线的均整效果不明显;高原子序数的铅、钨对X射线有一定的均整度，其离轴比和剂量离轴分布曲线在距离射野中心轴附近有一定的平坦区域，对称性较好，但边缘处的相对剂量波动超过±5%，未能达到国际电子委员会(IEC)规定的±3%标准［1］.图6为各均整器对应的离轴剂量分布曲线.可以看出，相对铝材料而言，重金属钨材料的均整器对应的X射线剂量利用率较低.

图5 单一材料均整器模体表面下10 cm深处X轴方向的离轴比Fig.5 OAR in 10 cm depth below the surface of phantom(single-material flattening filter)

图6 模体表面下10 cm深处X轴方向的离轴剂量分布Fig.6 Off-axis dose distribution in 10 cm depth below the surface of the phantom

考虑到低原子序数金属对X射线衰减程度较小，铜材料的均整器也产生了一定的均整效果，这里利用铝、铜两种金属制作了两层相嵌套的复合均整器，外锥几何尺寸如1.1节所述，材料为铝，内部小圆锥材料为铜，采用了多种不同尺寸分别进行计算.图6和图7记录了其中的两组曲线(标记为Al-Cu-1和Al-Cu-2).从这两组离轴剂量分布图和离轴比可以看出，只采用轻金属作为均整器材料很难将其离轴比和离轴剂量分布曲线中的凸起部分“消平”，要想实现X射线在治疗射野内的剂量平坦度要求，必须在射野中心轴附近适当加入高原子序数材料，通过重金属对X射线的衰减来降低射野中心轴附近的剂量值.

图7 模体表面下10 cm深处X轴方向的离轴比(复合材料均整器)Fig.7 OAR in 10 cm depth below the surface of phantom(multi-material flattening filter)

采用重材料铅锥嵌入铝锥中心处(见图4)，外锥尺寸如1.1节所述，内部铅锥底面半径为1.6 cm，高为2.6 cm.由于铅材料可使透射X射线能量有较大幅度的降低，而包围铅锥的铝材料对X射线的衰减程度较小，因此，这种设计不仅可以“消去”各离轴分布曲线中心处的凸起部分，还不会过分降低射野边缘区域的X射线剂量，进而在满足射野剂量平坦度要求的同时，达到提高X射线剂量利用率的目的.

由图6和图7中Al-Pb-1的离轴剂量分布和离轴比可以看出，射野中心轴附近有较宽的平坦部分，说明铝-铅复合材料均整器的均整效果已经得到了显著提高，但射野边缘剂量值的陡降程度不够理想，导致均整区域内最大吸收剂量点与最小吸收剂量点吸收剂量的比值超出了国标中规定的不大于106%的标准［14］.经过几次调整铅锥高度及底面半径大小，当铅锥底面半径调整为1.2 cm，高为2.2 cm时，得到了标记为Al-Pb-2的离轴分布曲线和离轴比，如图6和图7所示.图中可见，整个均整区域内，Al-Pb-2均整器下的X射线剂量分布平坦，且对称性好，区域边缘处剂量值急剧下降，均整区域内最大吸收剂量点与最小吸收剂量点吸收剂量的比值约为103%，完全满足GB 15213—94的要求［14］.对比图6中的各组离轴剂量分布曲线还可以看出，Al-Pb-2均整器下X射线剂量利用率较高.

为验证模体不同深度处的剂量分布是否理想，计算了模体表面下5和15 cm深度处X轴方向的离轴比和离轴剂量分布，结果如图8和图9所示.该结果与10 cm深度处的结果具有一致性.5 cm深度处X射线剂量分布均匀，治疗射野内剂量平坦度和对称性非常好，边缘区域剂量分布也满足要求;15 cm深度处的离轴比和剂量离轴分布曲线在均整区域内出现了小幅度波动，这主要是由于统计误差造成的，更精确的计算需要继续增大入射粒子数.

图8 模体表面下5 cm深处X轴方向的离轴比和离轴剂量分布Fig.8 OAR and off-axis dose distribution in 5 cm depth below the surface of the phantom

2.2 能量注量分布

能量注量(energy fluence)是以进入辐射场内某点处单位截面积球体的粒子总动能描述辐射场性质的一个量.能量注量离轴分布可以从能量角度反映出治疗射野剂量平坦度和对称性问题.图10为源皮距SSD为100 cm的治疗野平面上各均整器对应的能量注量离轴分布曲线.可以看出，X射线经各均整器后得到的能量注量分布差别很大，其规律与离轴剂量分布类似：低原子序数的铝、铜材料均整器下，能量注量在靠近射野中心轴附近较高，射野边缘较低;高原子序数的铅、钨材料均整器下，能量注量在射野内有较宽的平坦宽度，但射野边缘处剧降效果不明显，而且整体上能量注量值相对较低，反映出X射线剂量利用率较低.复合材料均整器(Al-Pb-2)对应的能量注量分布在射野内非常平整，均整区域内射线能量分布均匀，且能量注量值较高，说明X射线剂量利用率较高，边缘部分能量注量值急剧下降.

图9 模体表面下15 cm深处X轴方向的离轴比和离轴剂量分布Fig.9 OAR and off-axis dose distribution in 15 cm depth below the surface of the phantom

2.3 粒子角分布

图11为X射线经过复合材料均整器(Al-Pb-2)均整后的粒子角分布曲线，插图为放大后的电子和正电子角分布曲线.由图可见，光子角分布集中在0°～4°之间，前向性较好，利于临床治疗使用.正负电子角分布范围广，角度较大，这种分布会使其偏离出治疗射野外，不能进入模体，不会造成射野内带电粒子污染.射野外的带电子污染可通过辐射防护设计来解决.

图10 能量注量离轴分布Fig.10 Off-axis energy fluence distribution

图11 复合材料均整器(Al-Pb-2)下的粒子角分布Fig.11 Angular distribution for Al-Pb-2 flattening filter

2.4 粒子能谱分布

图12为X射线经过复合材料均整器(Al-Pb-2)后在治疗野平面上的粒子能谱分布图，插图为放大后的电子和正电子能谱分布图.由图可见，光子能量在0～16 MeV范围内呈连续分布，峰值出现在1 MeV附近，射野内光子平均能量约为3.81 MeV，电子和正电子能谱分布在数值上与光子能谱分布相差近3个数量级，说明带电粒子污染非常小.

2.5 百分深度剂量分布

图13为X射线经复合材料均整器(Al-Pb-2)均整后得到的水模体内深度分布曲线，SSD为100 cm.可以看出明显的X射线剂量建成区，最大剂量点约在模体下3.5 cm处，表面剂量小于37%，满足国标中规定的中心轴表面剂量不得超过最大剂量的60%的要求.由于最大剂量点不在表面，因此，在治疗深度肿瘤时可以很好地保护皮肤.

图12 复合材料均整器(Al-Pb-2)下的粒子能谱分布Fig.12 Energy distribution for Al-Pb-2 flattening filter

图13 复合材料均整器(Al-Pb-2)下的X射线深度剂量分布Fig.13 PDD for Al-Pb-2 flattening filter

3 结束语

本研究利用BEAMnrc程序设计了复合材料均整器.由以上分析可以看出，重金属材料对X射线的衰减程度较大，因此，在经过了几次对计算结果分析后，选择了两种金属相结合作为均整材料.采用尝试错误法多次调节材料各区域的相对厚度，即根据X射线束流分布特点，增大射野中心轴附近区域重金属材料的厚度，减小边缘区域重金属材料的厚度，最终使得X射线分布均匀，在均整区域内得到了平坦的剂量分布.经验证，所得到的射线前向性非常好，带电粒子污染也很小，说明该均整器的设计比较成功.另一方面，从价格上来说，铝、铅材料较传统的钨材料均整器更廉价更经济.当然，模体下15 cm深处的离轴剂量分布出现了小幅度波动，说明该均整器还可以通过调节模拟参数继续改进，更大射野下剂量分布是否平坦还需进一步验证.总之，利用蒙特卡罗方法对治疗头进行仿真模拟，通过分析处理得到的粒子能量、剂量分布等信息反复调制均整器参数，用于设计均整器是一种非常经济可行的方法.

［1］ 胡逸民.肿瘤放射物理学［M］.北京：原子能出版社，1999：171-174.

［2］ ROGERSD W O.Monte Carlo techniques in radiotherapy［J］.Physics in Canada，2002，58(2)：63-70.

［3］ 张洁熹，李泉凤.医用加速器电子治疗模式的BEAM程序分析［J］.原子能科学技术，2009，43(7)：664-672.

［4］ 陈朝斌，黄群英.蒙特卡罗方法在放疗计划中的应用［J］.核技术，2006，29(1)：22-28.

［5］ AYYANGARK M，KUMARM D，NARAYANP，et al.Monte Carlo simulation of a multi-leaf collimator design for telecobalt machineusing BEAMnrccode［J］.Medical Physics，2010，35：23-32.

［6］ 许淑艳.蒙特卡罗方法在实验核物理中的应用［M］.北京：原子能出版社，2006.

［7］ ROGERSD W O，FADDEGONB A，DINGG X，et al.BEAM：a Monte Carlo code to simulate radiotherapy treatment units［J］.Medical Physics，1995，22：503-524.

［8］ 李泉凤，严慧勇.用Monte Carlo方法设计X射线均整器［J］.清华大学学报，2003，43(6)：732-734

［9］ ROGERSDWO，WALTERSB，KAWRAKOWI.BEAMnrc users manual［R］∥ NRCC Report，PIRS-0509(A)revK.Canada：National Research Council of Canada，2005.

［10］ WALTERSB，KAWRAKOWI，ROGERSDWO.DOSXYZnrc users manual［R］∥ NRCC Report，PIRS-794 revB.Canada：NationalResearch Councilof Canada，2002.

［11］ MAC M，ROGERSD W O.BEAMDP users manual［R］∥ NRCC Report，PIRS-0509(C)revA.Canada：National Research Council of Canada，1999.

［12］ SHEIKH-BAGHERID，ROGERSD W O.Sensitivity of megavoltage photon beam Monte-Carlo simulations to electron beam and other parameters［J］.Medical Physics，2002，29(3)：379-390.

［13］ SAWKEYD，FADDEGONB A.Simulation of large X-rays fields using independently measured sourcegeometry details［J］.Medical Physics，2009，36(12)：5622-5632.

［14］ 国家技术监督局.GB 15213—94医用电子加速器性能和试验方法［S］.1994.