离轴超构透镜设计与特性分析

胡金高娃，赵尚男 ，王灵杰，叶昊坤，张建萍，张 新

（1.中国科学院长春光学精密机械与物理研究所,吉林 长春 130033；2.中国科学院大学,北京 100049）

1 引言

超构透镜是由二维超材料构成的平面光学器件，是在成像领域中具有较大应用潜力的超表面平面光学器件。其可以灵活操控光的相位、偏振、振幅等[1]，而且平面化的结构特点使其制造简单、插入损耗低。此外，超构透镜还能够以紧凑的形式实现对反射和透射光场空间分布的控制，已经成为当前的研究热点。

为了有效调控电磁波波前，传统透镜一般通过调控界面的几何形状或折射率来实现相位分布调控。但由于天然材料的介电常数和磁导率受限，现有的传统光学透镜通常尺寸较大、不易集成[2]。超构透镜通过调整单元结构的分布就可以得到所需相位分布，大大缩小了元件尺寸和体积。根据应用场合的不同，研究人员设计出了不同类型的超构透镜，如消色差超透镜[3-7]、基于超透镜的带通滤波器[8]、亚分辨率超构透镜[9-10]、彩色全息[11-13]、多功能超构透镜[14-17]和可重构超构透镜[18-20]等。

超构透镜分为共轴超构透镜和离轴超构透镜。其中，共轴超构透镜使光束聚集在轴上，离轴超构透镜是在共轴超构透镜上偏离中心截取一部分。它可使不同波长光束的轴线分开，相互分离地聚焦在原光轴上不同的点。其可以通过控制纳米单元的相位分布实现指定位置聚焦。相比于共轴超构透镜具有色散特性，可被应用于光谱仪中，为实现紧凑型光谱仪提供了新的思路。

2016 年，Khorasaninejad 等人基于离轴超构透镜研究了近红外波段的紧凑型光谱仪，光束的离轴角度最大在80°，大角度聚焦使超构透镜具有超色散特性，能够分辨小至200 pm 的波长差异，聚焦效率在30%左右。此外，通过拼接多个超构透镜可在宽波段内实现高分辨率[21]。2017年，Capasso 课题组同样基于离轴超构透镜研制了可见光波段的紧凑型光谱仪，光谱分辨率小至0.3 nm，总工作波长范围超过170 nm，并在一个基板上集成了多个具有不同数值孔径的超构透镜，使得其具备多种不同的光谱分辨率和灵活的工作波长范围[22]。同年，浙江大学马云贵课题组利用离轴超构透镜设计了波分解复用器[23]。该解复用器的光纤能量耦合效率可达89%以上，通道带宽约为9 nm。他们还对焦距和离轴角度产生的影响进行了研究。该研究对研制小型、紧凑的光通信解复用器件具有重要的指导意义。2018 年，该课题组使用波动光学和几何光学方法研究了基于离轴超构透镜的光谱仪的结构参数对有效光谱范围和光谱分辨率的影响。针对不同的用途，数值上提出了两种基于离轴超构透镜光谱仪[24]。2019年，Capasso 研究团队利用离轴超构透镜实现了一个具有纳米光谱分辨率的微型像差校正光谱仪，透镜到探测器的工作距离仅为几厘米，且基本上不因任何方式受到限制[25]。

然而，目前国内外对于离轴超构透镜的研究都存在着应用场景单一、特性分析不完备的局限性，需要进行更详细的参数分析来充分理解离轴超构透镜的特性。这些信息对基于离轴超构透镜的微小型器件设计至关重要。为了进一步提升离轴超构透镜设计参数对其分光聚焦能力的影响，本文提出了一种离轴超构透镜设计方法，并进行了不同参数的仿真，分析了离轴角度对光谱分辨率和聚焦效率的影响，分析了数值孔径对超构透镜的聚焦位置理论计算结果与仿真结果产生偏差的影响。本文研究为后续开展离轴超构透镜的设计和拓展应用提供参考。

2 离轴超构透镜工作原理

用于实现0～2π 范围内相位调制的超构透镜可分为三种类型：传输相位型、电路相位型和几何相位型[26]。本论文采用传输相位型离轴超构透镜。通过选定不同半径的纳米柱实现对0～2π 的相位覆盖。

如图1 所示，离轴超构透镜所在平面原点处相位为Φ(0)，离轴超构透镜上任意位置的相位为Φ(x,y)，选定聚焦位置F，若要光束聚焦在点F上，则相位需满足

图1 离轴超构透镜聚焦示意图Fig.1 Diagram of focusing an off-axis meta-lens

其中，xf、yf和zf为聚焦位置F点的坐标，f是离轴超构透镜的焦距，f=sqrt(xf2+yf2+zf2)。

根据式（1）得到聚焦位置为(xf,yf,zf)的离轴超构透镜相位分布函数[22]：

离轴超构透镜可实现任意位置的聚焦，并且对于不同波长的光，聚焦位置不同，具有一定的色散能力。选定聚焦位置后，通过式（2）可得到离轴超构透镜上离散的相位分布，以实现对入射光波的相位调制。

3 离轴超构透镜设计与特性分析

3.1 离轴超构透镜设计方法

本文所提的离轴超构透镜的设计方法中，为了避免偏振产生的影响，选用圆柱型单元结构。通过改变单元结构的半径，可获得0～2π 的相位覆盖，据此建立离轴超构透镜相位库。在选定设计参数后，根据公式（2）得到所需的相位分布。接着，在相位库中挑选与所需相位相近的单元结构，得到离轴超构透镜每个单元结构的半径分布，并根据获得的半径分布数据建立仿真模型，得到光场分布。当仿真结果与理论计算不符时，检查仿真结构的相位分布与理论计算的相位分布是否一致，若不一致，则建模出现问题，重新建模后再次仿真；若一致则建模正确，此时需考虑离轴超构透镜其他参数对仿真与理论计算结果产生的影响，设计流程图如图2 所示。

图2 离轴超构透镜设计流程图Fig.2 Design flowchart of off-axis mate-lens

根据表1 所示参数搭建单元仿真结构，选用高度为1 μm，单元周期T为500 nm 的离轴超构透镜单元结构，纳米柱材料为Si，基底材料为SiO2[27]。扫描不同半径的单元结构对应的相位，选取相位覆盖0～2π 的单元结构，建立在此参数下的相位库。不同半径单元结构对应的相位分布如图3 所示。

表1 离轴超构透镜设计参数Tab.1 Designed parameters of off-axis meta-lens

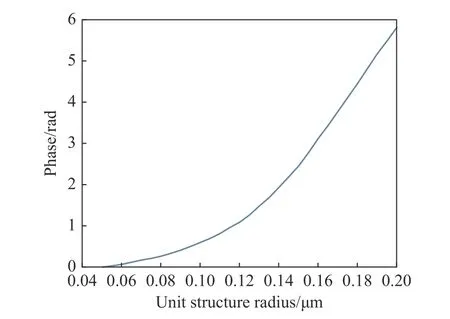
图3 不同半径单元结构对应的相位分布Fig.3 Phase distribution corresponding to unit structure with different radii

根据表1 参数，通过式（2）可以获得相位分布。本文采用Lumerical 软件，选取相位库中与所需相位相近的单元结构，进行离轴超构透镜建模，如图4（彩图见期刊电子版）所示。

图4 离轴超构透镜的（a）单元结构仿真示意图 及（b）仿真结构图Fig.4 (a) Schematic diagram of unit structure simulation and (b) simulated structure diagram of off-axis mate-lens

将监视器放在距离结构0.1λ位置处，并通过程序计算x-z平面远场的光场分布，获得的仿真结果如图5（彩图见期刊电子版）所示。

图5 离轴超构透镜的Lumerical 仿真结果图Fig.5 Simulation results of off-axis mate-lens by Lumerical

根据表1 中的离轴角度和焦距可以计算出该离轴超构透镜理论聚焦坐标为（7.420,0,32.141）（单位：μm）。如图5 所示，经Lumerical 仿真后离轴超构透镜将光束聚焦在（7.100,0,31.200）（单位：μm）处，与理论计算偏差在5%以内，证明设计方法正确。

3.2 对不同参数离轴超构透镜的影响分析

3.2.1 不同数值孔径对仿真结果的影响

图1 中离轴超构透镜的张角为β，数值孔径NA=sin(β/2)。可见，当离轴超构透镜的直径D与离轴角度α固定时，焦距f越长，则张角β越小，即NA越小。不同的NA会导致计算相位分布范围不同。图6（彩图见期刊电子版）为D=30 μm，α=13°，入射波长λ0=1.550 μm，焦距f=32.986 μm时离轴超构透镜的理论相位分布和Lumerical 仿真结果，此时NA=0.408。

图6 D=30 μm，α=13°，λ0=1.550 μm，f=32.986 μm 时的相位分布与仿真结果图Fig.6 Phase distributions and simulation results for D=30 μm,α=13°,λ0=1.550 μm,f=32.986 μm

图7（彩图见期刊电子版）为D=30 μm，α=13°，入射波长λ0=1.550 μm，焦距f=80 μm 时离轴超构透镜的理论相位分布和Lumerical 仿真结果，此时NA=0.180。

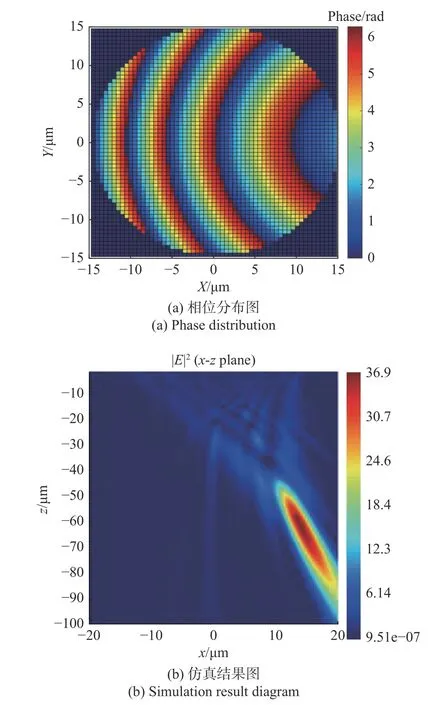
图7 D=30 μm，α=13°，λ0=1.550 μm，f=80 μm 时的相位分布与仿真结果图Fig.7 Phase distribution and simulation results for D=30 μm,α=13°,λ0=1.550 μm,f=80 μm

根据图6（a）和图7（a）可以看出，对于离轴超构透镜，当NA较小时，相位分布范围缩小，如图7（a）中相位右半部分被覆盖。对比表2 中不同NA的理论计算和仿真聚焦位置偏差，可知，NA越小，理论计算与仿真的偏差越大。偏差大小取决于相位缺失部分的大小。

表2 不同NA（不同焦距f）的离轴超构透镜理论计算与仿真聚焦位置对比Tab.2 Comparison of the focusing positions of off-axis meta-lens with different NA and different focal lengths obtained by theoretical calculation and simulation (Unit: μm)

上述情况为口径D相同、离轴角度α相同，改变焦距f，从而实现不同NA。当口径D与焦距f固定时，改变离轴角度α，同样会使NA发生变化，离轴角度α越大，NA越小。

选择D=30 μm，焦距f=32.986 μm，仿真分析离轴角度分别为α=27°（此时NA=0.388），和α=34°（此时NA=0.371）的情况。仿真结果如表3所示。

表3 不同NA（不同离轴角度d）的离轴超构透镜理论计算与仿真聚焦位置对比Tab.3 Comparison of the focusing positions of off-axis meta-lens with different NA and different offaxis angles obtained by theoretical calculation and simulation (Unit: μm)

对比表3 中不同NA的理论计算和仿真聚焦位置偏差可以得到与表2 相同的结论，即随着NA的减小，离轴超构透镜理论与仿真的聚焦位置坐标偏差会增大。该现象产生的原因是当口径和离轴角度一定时，数值孔径减小会导致相位覆盖范围减小。根据公式（2）可知，口径一定会使得超表面结构的坐标位置范围固定，NA越小，则焦距越长，离轴聚焦位置与坐标原点偏离程度越大，其相位分布的偏离趋势与图6（a）到图7（a）的一致。因此，随着NA的减小，在一定口径所在的坐标范围内，离轴超构透镜结构能覆盖到的有效相位范围有所减小。同理，当口径和焦距一定时，根据公式（2）可知，离轴角度越大（NA越小），一定口径所在坐标范围内的有效相位覆盖范围越小，仿真结果与上述规律一致。为了更准确地分析不同离轴角度对分辨率和聚焦效率的影响，缩小仿真结果与理论的偏差，后续的分析将选择NA为0.408 的超构透镜参数。

3.2.2 不同离轴角度对光谱分辨率和聚焦效率的影响

离轴超构透镜有一定的色散能力，当不同波长的光入射时，离轴超构透镜会将光束聚焦在不同位置。根据式（3）可以算出相应参数下离轴超构透镜的分辨率。

式中，f为离轴超构透镜焦距，为改变入射波长导致的聚焦位置的位移距离，如 图8 所示，F为离轴超构透镜的F数（F=f/D），λ0为设计波长，dλ为设计波长与工作波长的偏差，α为离轴超构透镜聚焦角度。

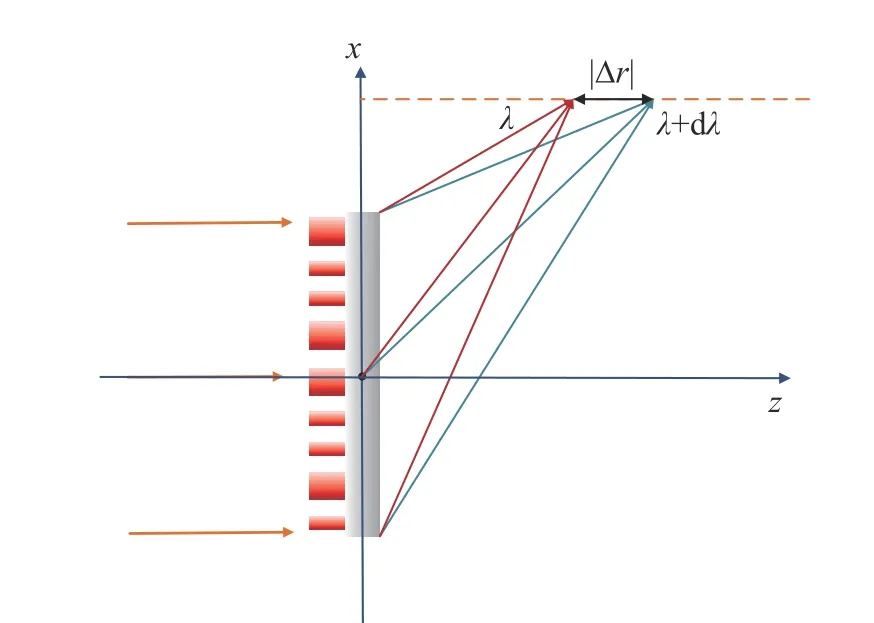
图8 示意图Fig.8 Schematic diagram of

当NA=0.408，λ0=1.550 μm，D=30 μm 时,分别仿真α=13°和α=20°时离轴超构透镜的色散特性，如图9（彩图见期刊电子版）所示。当NA相同时，不同离轴角度的离轴超构透镜相位覆盖范围相近。

图9 不同α 的离轴超构透镜相位分布图Fig.9 Phase distributions of off-axis meta-lens with different α

在α=13°，λ0=1.550 μm 时，根据公式（3）可以计算出该离轴超构透镜的最小分辨率为0.472 μm。在以工作波长λ0入射时，仿真表明x-z（7.100 μm,31.200 μm）处光强最大。在以工作波长λ1入射时，仿真表明x-z（7.161 μm,21.821 μm）处光强最大。为方便测量，将监视器放在设计波长对应的仿真光强最大位置处，即x=7.100 μm，观察λ0和λ1在Z方向的光强分布。如图10（彩图见期刊电子版）所示，对比λ0=1.550 μm和λ1=2.022 μm 仿真结果。

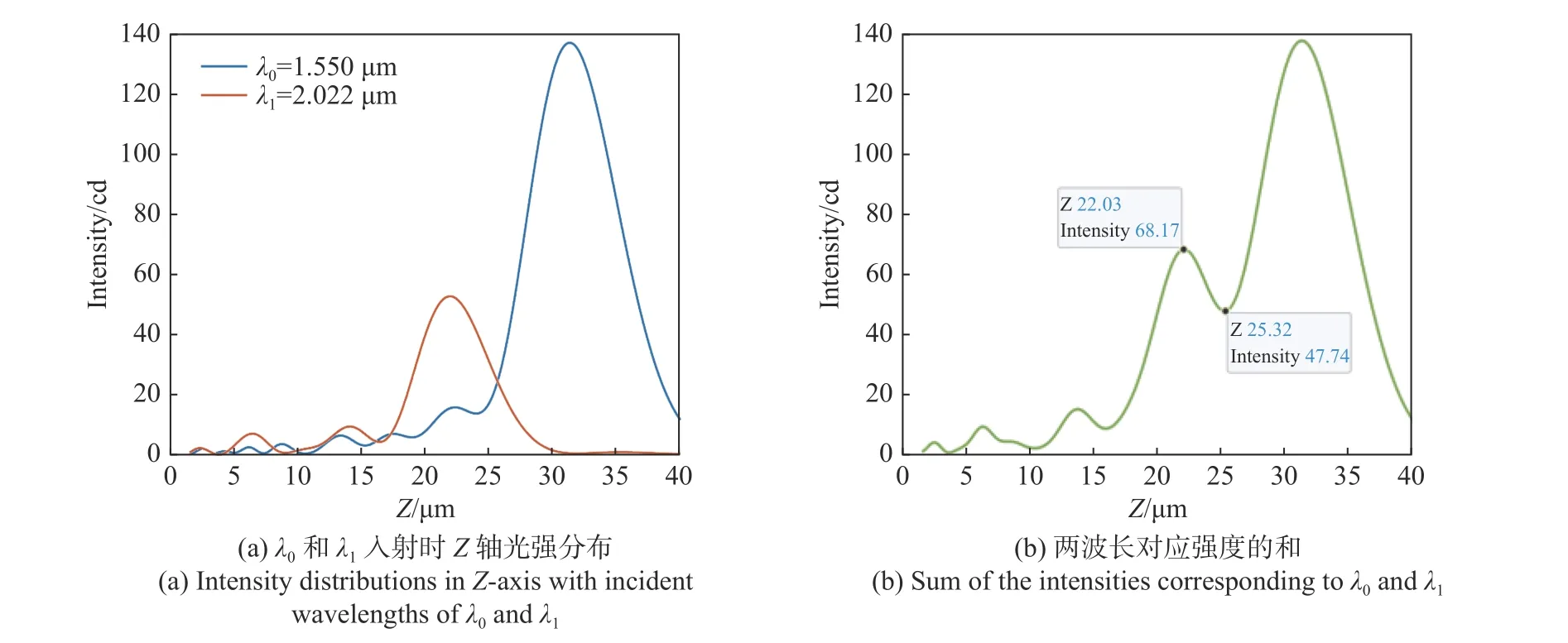
图10 α=13°,不同λ 入射时离轴超构透镜沿Z 轴的光强分布图Fig.10 The intensity distributions of the off-axis meta-lens along Z axis with different incident wavelengths when α=13°

在α=20°，λ0=1.550 μm 时，根据公式（3）可以计算出该离轴超构透镜的最小分辨率为0.306 μm。在以工作波长λ0入射时，仿真表明x-z（11 μm,30.400 μm）处光强最大。在以工作波长λ1入射时，仿真表明x-z（11.080 μm,23.586 μm）处光强最大。为方便测量，将监视器放在设计波长对应的仿真光强最大位置处，即x=11 μm，观察λ0和λ1在Z方向的光强分布。如图11 所示，对比λ0=1.550 μm 和λ1=1.856 μm 仿真结果。

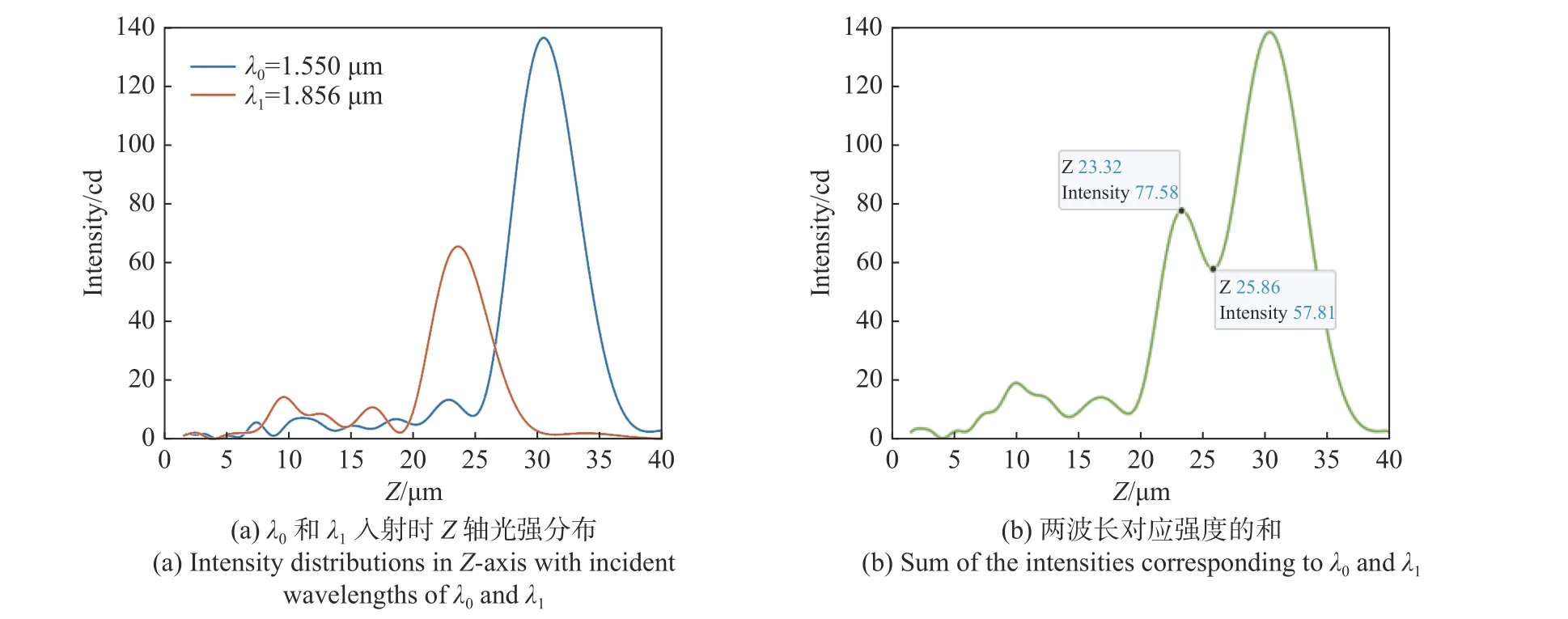
图11 α=20°,不同λ 入射时离轴超构透镜沿Z 轴光强分布图Fig.11 Intensity distribution of the off-axis meta-lens along Z axis with different incident wavelengths when α=20°

根据图10（b）和图11（b）可以看出两个极大值中间的极小值小于最小极大值的81%，满足瑞利判据，即可以分辨。

仿真结果表明，当NA一定时，离轴角度越大，光谱分辨率越小。

此外，对于离轴超构透镜，离轴角度的选择不仅对光谱分辨率有着重要的影响，还对其聚焦效率有一定的影响。需要说明的是，本论文中聚焦效率是利用焦斑能量与光源能量的比值计算得到的，其中，焦斑能量是在焦平面用焦点中心直径为3×FWHM 的圆对坡印廷矢量进行积分得到的，光源能量是利用焦平面的能量与透过率之比计算得到的[28-29]。通过控制变量法，设计波长为1.550 μm，数值孔径NA为0.408，仿真分析离轴角度分别为13°、20°、23°、30°、41°的离轴超构透镜。其聚焦效率分别是：59.14%、57.36%、55.46%、53.14%和49.70%，并绘制聚焦效率与离轴角度的曲线图，如图12 所示。

图12 NA=0.408 时，不同离轴角度对应的聚焦效率曲线图Fig.12 Curve of focusing efficiency corresponding to different off axis angles at NA=0.408

通过图12 可知，当NA和入射波长固定时，随着离轴角度的逐渐增大，聚焦效率会逐渐减小，根据之前的分析可知离轴角度增大，分辨能力增强。因此，若想同时保证高聚焦效率和高的光谱分辨率，离轴角度需要折衷选取。

此外，当NA和离轴角度α固定时，若入射波长偏离设计波长（1.550 μm），会导致聚焦效率大幅度下降，如表4 所示。

表4 离轴角度α=13°时不同工作波长对应的聚焦效率Tab.4 Focusing efficiencies at different working wavelength at the off-axis angle α=13°

本节分析了不同数值孔径对仿真结果的影响和不同离轴角度对光谱分辨率及聚焦效率的影响。随着数值孔径的减小，离轴超构透镜理论与仿真的聚焦位置坐标偏差会增大。这是因为数值孔径小会导致相位覆盖范围减小。仿真结果显示，随着离轴角度的增大，光谱分辨率会提升，该现象与公式（3）中反映的离轴超构透镜的光谱分辨率和离轴关系规律是一致的。此外，随着离轴角度的增大，聚焦效率会降低，这是因为离轴角度增加会导致离轴聚焦位置更加偏离光轴，从而使接收面的光强变小，聚焦效率则越低。

4 结论

本文介绍了离轴超构透镜的工作原理，并提出了一种离轴超构透镜设计方法。在此基础上，对不同参数产生的影响进行了分析。结果表明：数值孔径、离轴角度、入射波长的改变会对离轴超构透镜的聚焦位置、光谱分辨率和聚焦效率等产生影响。对于离轴超构透镜，数值孔径的减小会导致聚焦位置的理论与仿真结果偏差变大，以口径D=30 μm，离轴角度α=13°的超构透镜为例，NA=0.408 的仿真与理论聚焦位置偏差在1 μm 以内，而NA=0.180的偏差约为16.5 μm。同时，离轴角度越大，离轴超构透镜的色散特性会越强，则光谱分辨率越高，但聚焦效率会随之降低，以口径D=30 μm，NA=0.408 的超构透镜为例，α=20°的光谱分辨率为0.472 μm，聚焦效率是59.14%，α=13°的光谱分辨率为0.306 μm，聚焦效率是57.36%。设计者需根据不同的需求合理平衡离轴超构透镜的设计参数。本论文提出的离轴超构透镜设计方法以及特性分析结果可为后续基于离轴超构透镜的微小型结构设计以及应用提供一定的参考。