求解三维电磁场问题的改进的自适应区域分解算法

李 鹏， 孟令琴

(1.上海大学特种光纤与光接入网省部共建重点实验室，上海200072;2.东南大学毫米波国家重点实验室，南京210096)

很多电磁问题用理论分析来计算十分复杂，甚至不可能得到结果，因此需要通过数值计算得到问题的结果.1966年，Yee［1］首次提出一种新的电磁场数值计算方法——时域有限差分(finite difference time domain，FDTD)算法.该算法已广泛应用于电磁散射、电磁兼容、天线、波导与谐振腔系统、微波集成电路等问题的研究中.FDTD算法是以差分原理为基础，用离散点上的数值解来逼近连续场区域的真实解.随着研究的深入，各种提高FDTD算法的精度和速度的技术不断涌现.Xu等［2-4］提出了一种新的区域分解算法，该算法首先把计算区域分割成几个子区域，在每个子区域里面采用适合本区域的共形网格，然后分别计算各个子区域，最后在各个子区域边界上采取一种数据传递方案，综合可得整个区域的解.文献［5］将拓扑网络应用到FDTD算法中，把一个大问题区域分解成为几个相互独立的子区域，分别计算各个区域的散射参数，然后通过矩阵方程计算出总的散射参数，从而计算大区域上的电磁耦合和传输问题.文献［6］提出并验证了一种空间区域划分FDTD算法.该算法把一个大的计算区域分解为几个小的区域，并重复利用电脑有限的内存，从而可以解决大的电尺寸问题.然而这种方法会占用很大的硬盘空间和很长的计算时间.为了计算稀疏填充的大型多物体，文献［7-8］提出了一种多区域的FDTD(multiple region/FDTD，MR/FDTD)算法，达到了减少内存需要量和缩短求解时间的目的.文献［9-10］提出并验证了一种自适应区域分解(adaptive domain decomposition-FDTD，ADD-FDTD)算法.该算法将三维电磁场问题的求解区域分解为若干独立的子区域，在各个子区域之间通过连接边界条件进行自适应检测，以判断波是否能传播到子区域，以及子区域是否需要进行运算.该算法可以显著缩短计算时间.

本研究针对文献［9-10］中的自适应区域分解方法，提出了一种改进的自适应区域分解算法.在判断波是否传播到检测面的时候，不采用某点的电场值和预先设定的阈值比较，而是通过对检测面上的电场积分得到相应的电压，然后选取其中最大的一个电压值和预先设定的阈值比较.

随着半导体材料科学和通信电子技术的快速发展，20世纪60年代出现了微波集成电路(hybrid microwave integrated circuit，HMIC)，之后又出现了单片微波集成电路(monolithic microwave integrated circuit，MMIC)、三维微波集成电路，最后出现了微波多芯片组件(microwave multi-chip module，MMCM).由于现代通信的需要，微波电路工作频率不断提高，这使得MMIC的互连和封装越来越困难.互连是多芯片组件(multi-chip module，MCM)中的最关键技术之一，研究互连的特性问题可以提高集成电路集成度、速度和可靠性.对高速电路互连结构的分析过程中，采用频域分析方法计算所要求的宽频上的特性是十分耗时和繁琐的，而时域方法可以通过一次计算得到宽频上的频率响应.

为了验证所提出的算法在高速互连结构中应用的正确性，本研究选取了3个在高速电路互连结构中的常见结构，分别采用HFSS、原始FDTD算法、ADD-FDTD算法和IADD-FDTD算法进行了分析，证明了本研究提出的IADD-FDTD算法的正确性.

1 一种改进的ADD-FDTD算法

原始的ADD-FDTD算法中，各子区域之间在进行自适应区域检测时，通过选择相邻子区域边界面上的一点的电场值和预先设定的阈值进行比较.如微带结构中，取微带导带下方的中心线上一点的电场值作为检测值，取电场激励源最大幅值的0.001%作为阈值.但该算法有2个比较明显的缺点.

(1)在某些结构中，如图1所示的多条平行微带线结构中，有N条平行的微带线，原始的ADDFDTD算法只是简单地选择检测面上其中一条微带线导带下的电场Ei作为检测值.如果Ei在检测面上的所有电场值中并不是最大的，就可能出现波其实已经传播到此子区域，但是当前的计算并没有包含此子区域，从而造成计算结果的错误.

图1 多条平行微带线结构Fig.1 Parallel multi-microstrips structure

(2)原始ADD-FDTD算法中，如果检测面与不连续结构距离过大，则整个计算区域只能分成很少的几个子区域，不能充分发挥ADD-FDTD算法通过划分子区域来提高计算效率的作用.如果检测面距离不连续结构很近，则检测面上有的点的电场值可能存在不稳定的情况，这就会出现虚假的较大的电场值.在检测时如果选择检测面上的最大电场值的点作为检测点，则容易出现其实波并没有传播到检测面上，但是由于某点不稳定而造成了较大的电场值，程序就会认为波已经传播到了下一个子区域，从而将下一个子区域加入迭代，这样就会削弱ADDFDTD算法运算时间短、运算效率高的优点.

针对原始ADD-FDTD算法中的不足，本研究提出一种改进的ADD-FDTD算法，其流程图如图2所示.从图中可以看出，IADD-FDTD算法的步骤如下：首先，对整个区域初始化赋0值，根据实际计算的物理结构将计算区域分为Z0个区域，令Z的初始值等于1;然后，开始时间循环，对Z个子区域内的电场值和电压值进行更新，其余Z0－Z个子区域的值不变.对于子区域之间边界上的电场进行积分得到电压，根据这些电压值判断电磁波是否传播到了下一个子区域.如果没传播到，则直接开始下一个时间循环，如果传播到了下一个子区域，则Z值加1以后再进入下一个时间循环.这样一直循环下去，直到时间步进结束.

图2 IADD-FDTD算法流程图Fig.2 Flow chart of IADD-FDTD method

本算法在判断波是否传播到检测面时，并不采用原始ADD-FDTD算法中的方法，即将某点的电场值和预先设定的阈值Eon比较，而是通过对检测面上的电场积分得到相应的电压，然后选取其中最大的一个电压值和预先设定的阈值电压进行比较.图3是一个沿着z轴放置的微带结构，ABCD面代表其中的一个检测面.设结构沿x方向划分了i+1个网格，那么在ABCD面上沿虚线积分可以得到i个电压值V1，V2，…，Vi，选择其中最大的值Vx和阈值Von相比较，如果Vx＞Von，则认为波已经传播到了检测面;如果Vx＜Von，则认为波还未传播到检测面.阈值Von的选取是令Ey等于电场源的最大值的0.001%，然后乘以dy再乘以y方向上的网格数目J得到的.

图3 检测面示意图Fig.3 Schematic drawing of test surface

首先，由于对检测面上的1，2，…，i的所有Ey分别进行积分得到V1，V2，…，Vi，然后取其中的最大值和Von进行比较，这样在计算有多条平行微带线结构时，就不会出现选择的点不是边界面上的最大场值点的问题，从而确保了不会出现波已经传播到下一子区域而计算中却没有包含下一子区域的情况.

其次，由于采用了电压检测，即使某点电场由于不稳定而造成了较大的电场值，该电场值在整个积分中的影响也很小.也就不会出现程序由于错误的最大电场值，而认为波已经传播到了下一个子区域，从而将下一个子区域加入迭代的情况.这表明本研究提出的算法具备一定的抗干扰性.另外，由于检测面和不连续结构不需要相隔太远，因此可以对计算区域进行更为密集的子区域划分.

2 数值计算

下面举例对高速电路中常见的微带结构进行分析，包括三维微带结构和多层微带电路互连结构(单通孔结构和双通孔结构)，以证明本研究提出的IADD-FDTD算法的正确性和有效性.

2.1 微带线结构的分析

在高速微波电路中，微带线是应用最广泛的微波信号传输线.本算例采用FR4材料的PCB板，尺寸为20 mm×20 mm，介电常数εr=4.5，介质高h= 0.7 mm，微带线宽W=1.2 mm.具体结构如图4所示.

图4 微带互连线Fig.4 Microstrip interconnection line

为了将数值色散减少到可以接受的水平，空间网格步长需要满足［11］：

式中，Δhmax表示Δx，Δy和Δz的最大值，λmin为计算频率范围内波长的最小值.综合考虑所计算结构的尺寸，这里取Δx=Δy=Δz=0.1 mm.

空间和时间离散间隔应该满足Courant稳定性条件［11］：

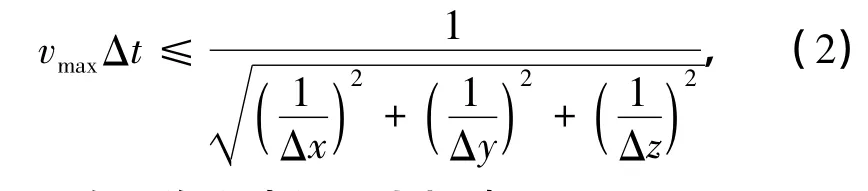
式中，vmax为工作模式的最大相速.

根据以上条件，并考虑到计算频率和合理的迭代次数，选择Δt=0.18×10－12s.

在导带下面的切面上均匀设置激励源，即

式中，t0=6T，T=25Δt.

微带地板和导带均设置成理想金属导体(perfect electric conductor，PEC)，在介质板上方设置10层空气层，四周包裹单轴各向异性介质完全匹配层(uniaxial perfectly matched layer，UPML)，总网格数为220×220×27.首先，在Ansoft HFSS软件中建模仿真微带线结构;然后，分别用原始FDTD，ADDFDTD和IADD-FDTD 3种算法通过Matlab编程进行仿真.采用ADD-FDTD算法仿真时，将微带结构沿z轴分成5个子区域，而采用IADD-FDTD算法仿真时，将微带结构沿z轴分成8个子区域.图5给出了采用4种方法仿真得到的散射参数曲线.

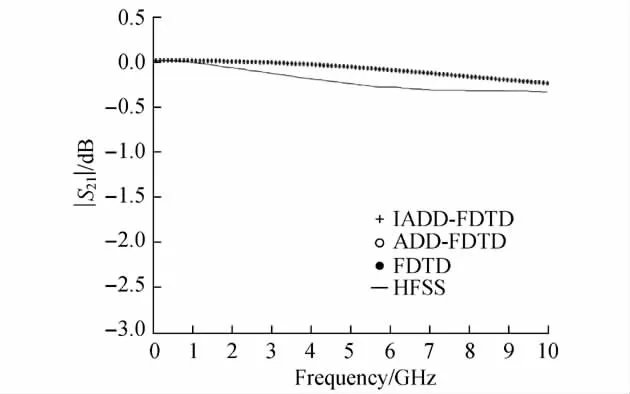
图5 微带线的频率响应Fig.5 Frequency response of microstrip

由图5可知，采用3种算法计算的结果完全相同，另外，3种算法和HFSS仿真得到的结果也比较吻合.ADD-FDTD算法比原始FDTD算法节省约6.80%的计算时间，而本研究提出的IADD-FDTD算法比原始FDTD算法节省约10.98%的计算时间.

2.2 多层印刷电路板结构中微带单通孔互连结构的分析

随着电路小型化的需求，印刷电路板(printed circuit board，PCB)更多地采用多层结构，这样就可以将传输线放在不同的层，在不同走线之间用接地板进行屏蔽以减少相互间的干扰.这些不同层的传输线之间通过通孔连接，由于电路的结构越来越复杂、传输速率越来越快、工作频率越来越高，使得由于互连和封装所引起的寄生效应在实际电路设计过程中变得越来越不容忽视，其中比较突出的问题就是多芯片结构的垂直通孔互连的分析.

本算例的具体结构如图6所示，其中 L= 25.2 mm，W=13.9 mm，T=3.2 mm，Wm=3.3 mm，D1=0.7 mm，D2=3.9 mm，D3=3.9 mm，介质的介电常数为3.4.

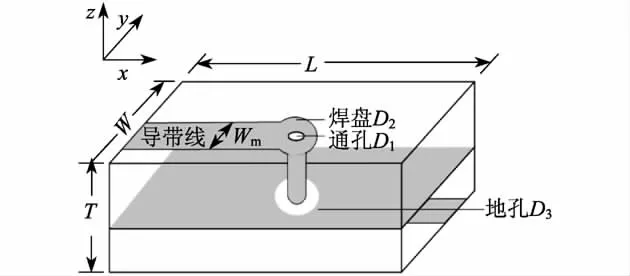
图6 单通孔互连结构Fig.6 Interconnection structure of single through-hole

在进行空间网格划分时，x方向和y方向的空间步长均为0.1 mm，z方向的空间步长为0.2 mm;时间步长Δt=0.1×10－12s.激励源和2.1节中的算例相同，将激励源加在10Δx处微带线下方的平面上.波出射面选择在距离右边界10Δx的平面上.

在计算区域周围采用一阶Mur吸收边界条件，总划分网格为252×139×32.由于原始ADD-FDTD算法采用电场检测，要求检测边界与不连续结构的距离较远，所以只能划分成4个区域.而 IADDFDTD算法由于采用电压检测，不需要检测边界和不连续结构相隔太远，所以在程序中可以划分6个区域.图7给出了采用4种算法仿真得到的0～20 GHz的散射参数曲线.

由图7可知，原始FDTD，ADD-FDTD和IADDFDTD 3种算法的计算结果完全相同，另外，3种算法和HFSS仿真得到的结果也比较吻合，从而验证了本研究提出的算法的正确性.ADD-FDTD算法比传统FDTD算法节省约5.88%的计算时间，本研究提出的IADD-FDTD算法比传统FDTD算法节省约10.61%的计算时间.

图7 单通孔的频率响应Fig.7 Frequency response of single through-hole

2.3 多层PCB结构中双通孔互连结构的分析

在多层PCB结构中往往采用多个通孔对微带进行互连，多个通孔之间会产生干扰，本算例以2个通孔为例进行分析.由于FDTD算法中的基本计算单元是矩形网格，为了计算简便，本算例用方形柱来代替实际应用中采用的圆柱.采用的板材为FR4材料，其介电常数εr=4.5，PCB板尺寸为30 mm× 17.6 mm，此结构共有2层，每层高为0.8 mm.矩形方柱的尺寸为0.8 mm×0.8 mm×1.6 mm，地层上的矩形反焊盘尺寸为1.6 mm×1.6 mm，顶层和底层上的所有微带线长度均为 10.8 mm，宽度为1.6 mm，具体结构和尺寸如图8所示.

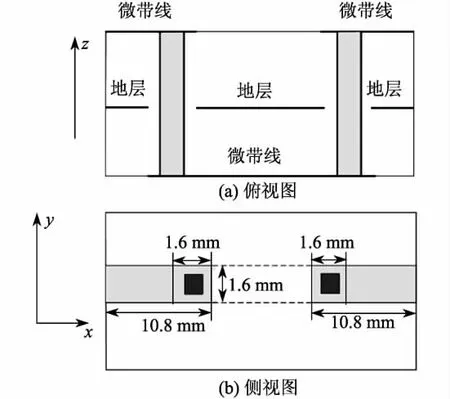
图8 双通孔互连结构Fig.8 Interconnection structure of double through-holes

对该结构进行空间网格划分时，x，y，z方向上的空间步长均为0.2 mm;时间步长 Δt=0.385× 10－12s.激励源和2.1节中算例相同，将激励源加在10Δy处微带线下方的平面上.

在z方向上，器件上下包裹10层空气层，四周各设置10层UPML吸收边界条件.总的网格数为170×108×48.分别采用HFSS，FDTD，ADD-FDTD和IADD-FDTD算法对该结构进行仿真.采用ADDFDTD算法时将待解问题分成4个区域，采用IADDFDTD算法时将待解问题分成6个区域.图9给出了4种算法仿真得到的0～20 GHz的散射参数曲线.

图9 双通孔结构的频率响应Fig.9 Frequency response of double through-holes

由图9可知，FDTD，ADD-FDTD和IADD-FDTD 3种算法的计算结果完全相同，另外，3种算法和HFSS仿真得到的结果也比较吻合，从而验证了本研究提出的算法的正确性.ADD-FDTD算法比传统FDTD算法节省约7.12%的计算时间，本研究提出的IADD-FDTD算法比传统 FDTD算法节省约12.67%的计算时间.

3 结束语

相对于传统FDTD和ADD-FDTD算法，本研究提出的IADD-FDTD算法消除了不稳定点对程序的影响，进一步提高了运算速度.对高速互连电路中常见的3种结构，分别用原始FDTD，ADD-FDTD和IADD-FDTD算法进行了Matlab编程仿真.3种算法的计算结果完全一致，并且和HFSS仿真得到的结果也非常吻合.

由于本研究提出的算法可以减少检测面上不稳定点造成的影响，从而可以进行更密集的分区，这也使得本研究提出的算法更能节省计算时间.这个优点在计算复杂结构和电的大尺寸问题时表现得更为明显，可以节省更多的计算时间.

另外，由于本研究提出的算法采用了分区域检测的方法，因此可以在不同的子区域内分别建立不同的计算模型，提高了解决复杂问题的精度.这对于计算区域较大、集成度较高的高速电路也是非常适合的.

［1］ YEEK S.Numerical solution of initial boundary value problems involving Maxwell’s equations in isotropic media［J］.IEEE Transactions on Antennas Propagation，1966，14(5)：302-307.

［2］ XUF，HONGW.Domain decomposition FDTD algorithm for the analysis of a new type of E-plane sectorial horn with aperture field distribution optimization［J］.IEEE Transactions on Antenna and Propagation，2004，52 (2)：426-434.

［3］ XUF，HONGW，ZHUX W.A new time domain near field to farfield transformation forFDTD in two dimension［C］∥ IEEE MTT-S International Microwave Symposium Digest.2002：2057-2060.

［4］ XUF，HONGW.Accurate analysis of microstrip patch antennas using FDTD method［C］∥ International Conference on Computational Electromagnectics and Its Applications Proceedings.1999：214-217.

［5］ WANGJ Y，GAOB Q.A hybrid method on calculating EM coupling in large problem space［C］∥International Symposium on Electromagnetic Compatibility Proceedings.1997：442-445.

［6］ XUEZ H，GAOB Q，LIUR X，et al.Space-divided FDTD method［C］∥ International Symposium on Electromagnetic Compatibility Proceedings.1999：568-571.

［7］ JOHNSONJ M，YAHYAR S.Multiple region FDTD (MR/FDTD)and its application to microwave analysis and modeling［C］∥IEEE MTT-S Symposium Digest.1996：1475-1478.

［8］ JOHNSONJ M，YAHYAR S.MR/FDTD：a multipleregion finite difference time domain method［J］.Microwave and Optical Technology Letters，1997，14 (2)：101-105.

［9］ 张华，洪伟，郝张成，等.一种采用边界检测的自适应区域分解时域有限差分方法［J］.应用科学学报，2005，23(5)：493-496.

［10］ 张华，洪伟，郝张成.求解三维电磁问题的自适应区域分解FDTD方法［J］.电波科学学报，2006，21(3)：397-402.

［11］ 葛德彪，闫玉波.电磁波时域有限差分法［M］.西安：西安电子科技大学出版社，2002：25-31.