Schrödinger方程的交替方向Legendre谱元法

曾凡海， 马和平， 赵廷刚

(上海大学理学院，上海200444)

谱方法是求微分方程数值解的重要方法之一，但在实际应用中会受到一些制约.对于高维问题，其导出的代数方程组规模很大，给求解造成困难，且计算量大.解决的方法之一是使用交替方向隐式(alternating direction implicit，ADI)方法，把高维问题转化为低维问题进行计算求解［1-2］.

单区域谱方法难以直接应用于复杂区域，但是通过区域分裂方法能较好地解决这一困难［3］.将区域分解成若干个子区域，在每个子区域上分别使用谱方法，可以降低导出的代数方程组系数矩阵的规模，改善矩阵的条件数，减少存储，并实现并行计算.

本工作首先考虑如下形式的线性Schrödinger方程：

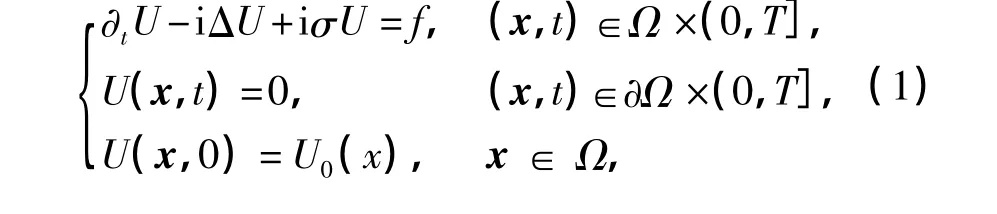
式中，Ω=(0，1)×(0，1)，∂Ω为Ω的边界，i2=-1，Δ为Laplace算子，σ=σ(x，y，t)为实值函数，U，U0，f为复值函数.Schrödinger方程是量子力学中最基本的方程，在高能物理、非线性光学以及超导等领域有着非常广泛的应用.

对Schrödinger方程的数值解已开展了许多研究工作.文献［4］建立了方程(1)的ADI正交样条配置法，文献［5］给出了方程(1)在f=0，σ=0时，时间和空间方向上具有二阶精度的ADI差分格式.关于非线性 Schrödinger方程的 Galerkin逼近可见文献［6-8］.

本工作提出一种交替方向Legendre谱元方法求解二维线性和非线性Schrödinger方程.该算法的优点在于其计算的高度并行化，并可以减少存储.该算法利用ADI方法把二维问题转化为一维问题进行求解，同时利用区域分裂法，可以并行计算.对于线性情形给出了方法的最优H1误差估计.最后的数值算例显示，该方法在时间方向具有二阶精度，空间方向具有谱精度.

1 记号与约定

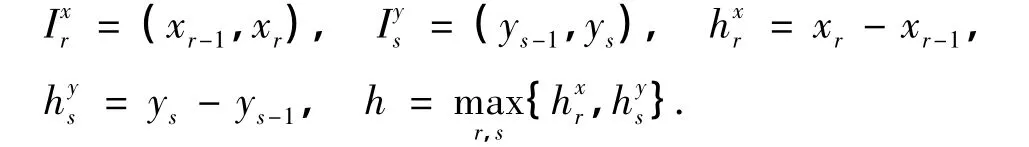
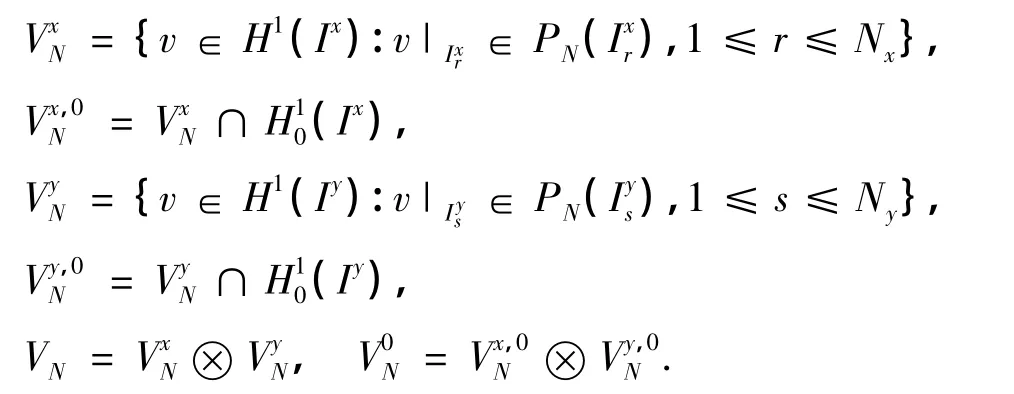
记L2(Ω)为通常的Hilbert空间，其上的内积和范数分别记为(·，·)和‖·‖L2.对于非负整数 r，Hr(Ω)为Sobolev空间，其上的半范数和范数分别为|·|Hr和‖·‖Hr.设 X为赋范线性空间，简记L2(X)=L2(0，T;X)和Hr(X)=Hr(0，T;X)，其上的范数记为‖·‖L2(X)和‖·‖Hr(X).

2 格式和算法实施

设τ为时间方向步长，{tk}为区间［0，T］的一个等距划分，即tk=kτ，τ=T/nT.记

2.1 交替方向Legendre谱元格式

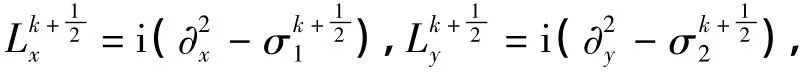
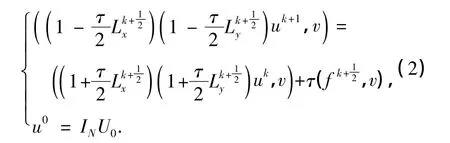
2.2 格式的矩阵表示和计算

假设σ1=σ1(x，t)，σ2=σ2(y，t)，令

则由方程(2)得到矩阵方程

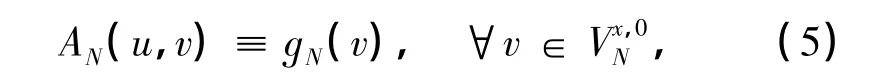
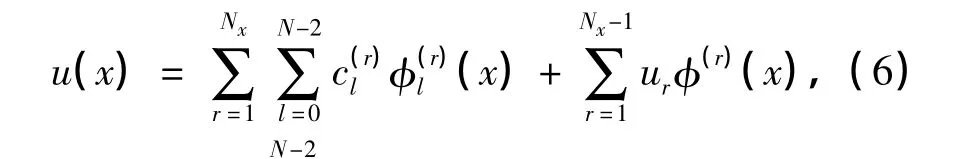
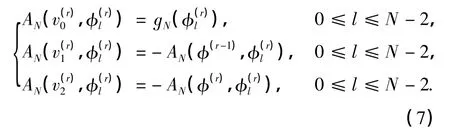
因此，可以得到

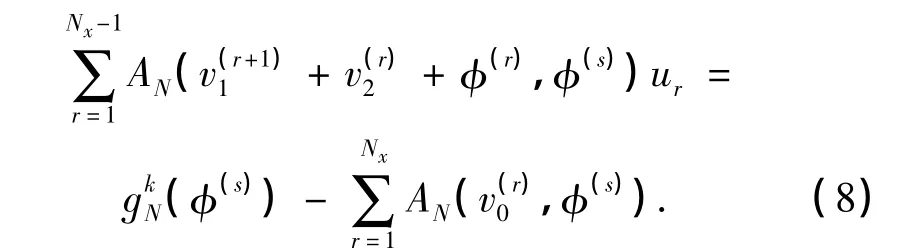
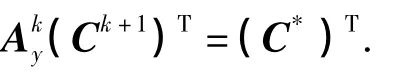
以下给出交替方向Legendre谱元格式(2)的一个收敛性结果.

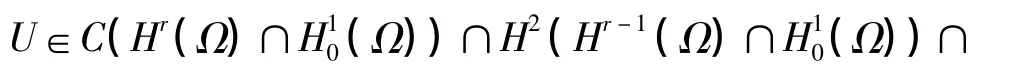
3 非线性Schrödinger方程

将交替方向谱元法应用到如下的非线性Schrödinger方程：

式中，F(U)为关于U的非线性函数.为了便于计算，采用三层格式，对非线性项显示处理.方程(10)的交替方向Legendre谱元格式如下：找uk∈，使得对于任意的v∈(1≤k≤nT-1)，成立

其求解过程和线性情况完全类似.

4 数值算例

例1 考虑如下线性Schrödinger方程：

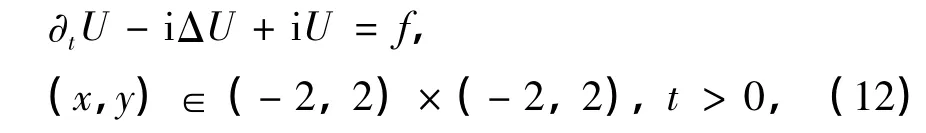
取其精确解为

分别在单区域和2×2区域上使用格式(2)计算，结果如表1所示.

表1 格式(2)在t=1时的最大模误差Table 1 Maximum error at t=1 for the Scheme(2)

由表1可以看出，格式(2)的单区域和2×2区域的结果在时间方向都具有二阶精度，空间方向具有谱精度.取较小的时间步长τ=1E-5以检验空间误差，可见，格式(2)的2×2区域的结果比单区域要好.

例2 考虑如下非线性Schrödinger方程［9］：

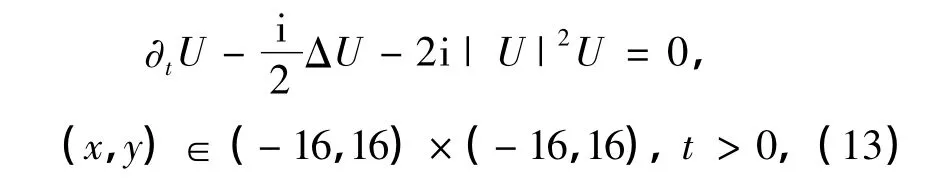
其精确解为

使用格式(11)在单区域上计算，结果如表2所示.

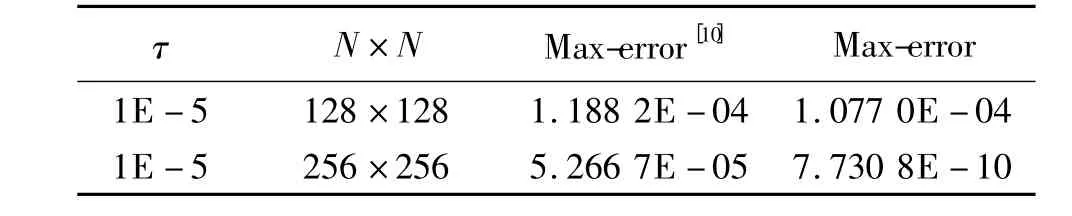
表2 方法(11)与文献［10］中的方法在t=0.5时的误差比较Table 2 Error comparison between the Scheme(11)and Reference［10］at t=0.5

此为文献［10］中的一个算例，在时间方向上采用二阶精度的时间分裂法，空间方向采用单区域Chebyshev-Tau方法.由表3可以看出，本工作采用格式(11)的计算结果要好于文献［10］中的计算结果.

［1］ DOUGLASJ，Jr.，DUPONTT.Alternating direction Galerkin methods on rectangles［C］∥ Proc symposium on Numerical Solution of Partial Differential Equations-Ⅱ.1971：133-214.

［2］ DENDYJ E.An analysis of some Galerkin schemes for the solution of nonlinear time dependent problems［J］.SIAM J Numer Anal，1975，28：541-565.

［3］ ORSZAGS A.Spectral methods for complex geometries［J］.Journal of Computational Physics，1980，37：70-92.

［4］ LIB K，FAIRWEATHERG，BIALECKIB.Discrete-time orthogonal spline collocation mehods for Schrödinger equtions in two space varialbles［J］.SIAM J Numer Anal，1996，35：453-477.

［5］ DENDY JE.An alternatingdirection method for Schrödinger’s equation［J］.SIAM J Numer Anal，1977，24：1028-1032.

［6］ AKRIVISG D，DOUGALISV A.Onaclassof conservative，highly accurate Galerkin methods for the Schrödinger equation［J］.RAIRO Model Math Anal Numer，1991，25：643-670.

［7］ AKRIVISG D，DOUGALISV A，KARAKASHIANO A.On fully discrete Galerkin methods of second-order temporal accuracy for the nonlinear Schrödinger equation［J］.Numer Math，1991，59：31-53.

［8］ KARAKASHIANO A，AKRIVISG D，DOUGALISV A.On optimal order error estimates for the nonlinear Schrödinger equation［J］.SIAM J Numer Anal，1993，30：377-400.

［9］ SHENJ.Efficient spectral-Galerkin method(Ⅰ)—direct solvers for second-and fourth-order equations using Legendre polynomials［J］.SIAM J Sci Comput，1994，15：1489-1505.

［10］ WANGH Q.An efficient Chebyshev-Tau spectral method for Ginzburg-Landau-Schrödinger equations ［J］.Computer Physics Communications，2010，181：325-340.