多普勒效应的最简规律

雷裕波

(昭平中学 广西 贺州 546800)

当波源与观测者之间存在相对运动时，观测者观测到的频率与波源发射波的频率不同，这种现象就是多普勒效应．引起多普勒效应的根本原因在于波源与观测者之间存在相对运动．在低速传播的机械波里所产生的多普勒效应比较容易掌握.然而当波源或观测者的运动速度较高时，必须要考虑时空变换的相对效应，此时的多普勒效应会遵循怎样的规律呢？本文就从洛伦兹时空变换的角度，阐述各种情形下的多普勒效应，并从中总结出多普勒效应所遵循的最简规律 ．

1 纵向多普勒效应

设有三个惯性参照系，如图1所示．

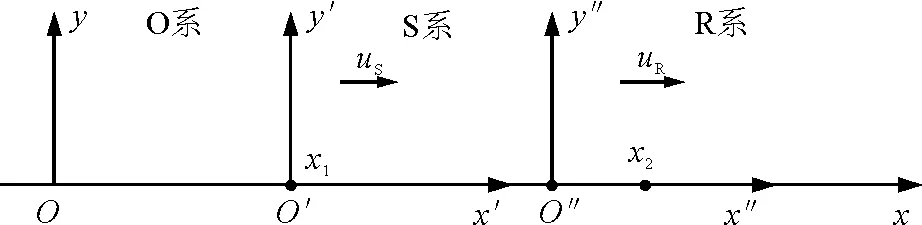
图1

媒质(场)参照系，即静系，简称O系，相应的坐标系为xOy．

波源参照系，即动系，简称S系，以波源S所在处为坐标原点，建立坐标系x′O′y′．

观测者参照系，即动系，简称R系，以观测者R处为坐标原点，建立坐标系x″O″y″．

由图1可看出,O、S、R系的x轴重合,令t=0时刻，O、O′、O″三原点重合，S系以速度uS、R系以速度uR同时沿O系的x轴正方向运动，此时波源S在O处发射第1个波峰，至t时刻，S系运动到O系的x1处，波源恰好发射第2个波峰，且第1波峰以速度vφ(相对O系)运动到O系的x2处，在S系及R系上表示t时刻的这两个相邻波峰的相应坐标分别如下：

O系：(0，0) (x1，t) (x2，t)

S系：(0，0) (x1′，t1′) (x2′，t2′)

R系：(0，0) (x1″，t1″) (x2″，t2″)

由洛伦兹的时空变换得

对S系：

(2)

(4)

对于R系，有完全相似的关系式.

由(1)、(2)式得

由(3)、(4)两式得

由此可见，t2′与t1′在S系上看来并非同一时刻，即x2′-x1′不是在S系观测到的波长.由于t2′比t1′早|Δt′|时间,所以在S系观测到的波长应为

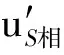
联立前面有关各式，解得

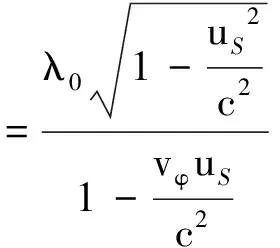
设TS为波源发射波的周期，则

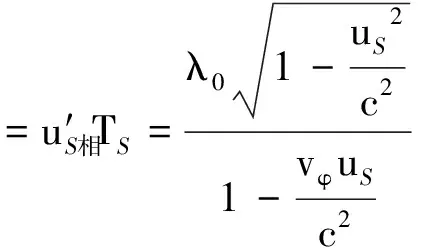
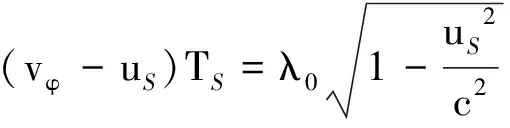
(5)

同理，在R系中不难得到

(6)

(6)式中，TR为在R系上的观测者所观测到的周期．

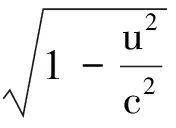
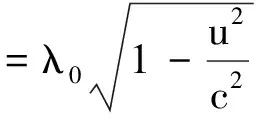
若不考虑动系相对静系的时空收缩效应,则λ洛=λ0；此时多普勒效应属于伽利略变换下的效应.若设T0为波在静系里沿u方向传播的周期，则λ0=vφT0.据洛伦兹变换知，当静系里的时间间隔为T0时，在动系里测得的时间间隔便为

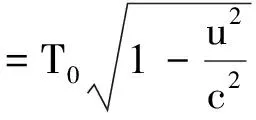
于是λ洛=vφT洛，显然在r0方向上亦有

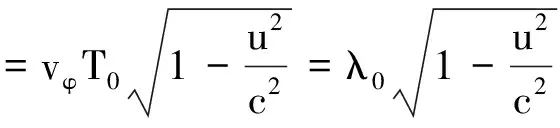
此时T0、λ0则分别表示波在静系里沿r0方向上传播的周期和波长，且有可能发生变化.例如当波源运动时，沿u方向传播的波波长λ0最小,而沿与u相反方向传播的波波长λ0最大，在垂直于u方向上传播的波λ0取值在此两者之间，但通常情况下λ0不必求出．于是(5)、(6)式可写成统一式

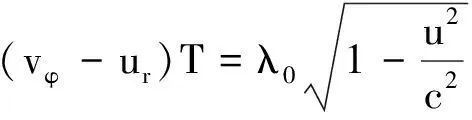
(7)

由此可见上述(5)、(6)两式应视作(7)式的特殊情形；然而(7)式的正确性及普遍性还有待于后面进一步的论证．

设

由(5)、(6)式得

(8)

(8)式为纵向多普勒效应的频率公式.显然对于机械波，由于波速vφ及波源或观测者的运动速度都远小于光速，相对效应很不明显，所以有

(9)

(9)式就是机械波的纵向多普勒效应的频率关系式，据此式可知，当观察者运动的方向与传向观测者的波的传播方向相同时，uR>0，使观测到的频率fR降低，反之升高.当波源的运动方向与传向观测者的波的传播方向相同时，uS>0，使观测到的频率升高，反之降低．

对于光波而言，vφ=c，当uR或uS比较大时，相对效应较明显，此时由(8)式得

设u为观测者相对波源的相对运动速度，据洛伦兹速度变换关系有

于是上式变为

(10)

由(10)式知，当观测者远离波源运动时，u取正，使观测到的频率降低；当观测者靠近波源运动时，u取负，使观测到的频率升高．当u≪c时，即观测者相对波源做低速运动时，(10)式可化为

即

Δf为由多普勒效应所引起的频移量．

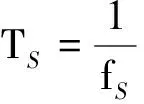
与前面的(7)式对比，此式应有类似的物理意义．

以上推导得出的(8)、(9)、(10)式，其正确性可从另外的角度加以证明(略)，从而知(7)式适用于纵向多普勒效应．

2 横向多普勒效应

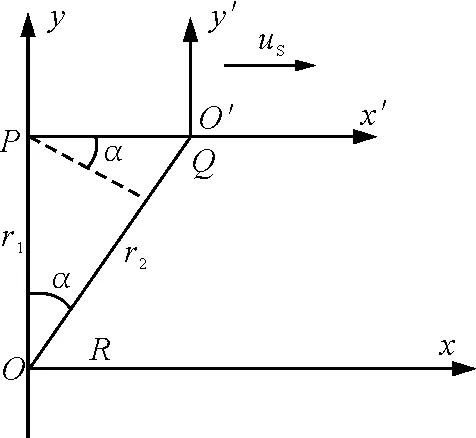
图2

如图2所示，观测者相对媒质静止，以观测者R处为原点O，建立静止的参照系R，以波源S处为原点O′，建立运动的参照系S，两系的x轴相互平行.在R系看来，t=0时刻，波源S位于R系的y=r1的P处，并以速度uS沿x轴正方向匀速运动，同时波源发射的波沿y轴负方向传向观测者R处．设波源的周期为TS，频率为fS，观测者观测到的周期为TR，频率为fR，如果前述(7)式依然适用，则对观测者即R系而言，因为uR= 0，所以

而

由λR伽=λR洛得

fR=f0

(11)

对波源即S系而言，因波沿y轴负方向传向观测者，故伽利略相对速度为vφ,所以有

由λS伽=λS洛得

(12)

由(11)、(12)两式得

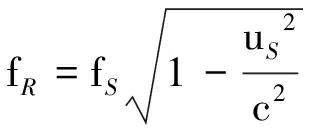
(13)

(13)式为横向多普勒效应的频率关系式,其正确性可作如下证明：如图2所示，设相对R系波的圆频率为ωR,相对S系波的圆频率为ωS.在R系上看，经一微小时间Δt，波源沿x轴正方向由P处运动到Q处，在S系上看相应的时间为Δt′，波振动的位相差为Δφ′=ωSΔt′；而在R系上看，观测者接收到分别由P、Q两处传来的两次波振动,其位相差应为

式中r2为Q,O间的距离．当Δt很小时，α很小，则此式中

故

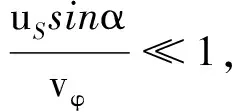
再利用ωS=2πfS及ωR=2πfR，便得

此式与(13)式相同，表明：

(1)上面的(7)式适用于横向多普勒效应；

(2)横向多普勒效应不如纵向多普勒效应明显, 因为当uR=0时,有

对机械波而言，uS≪c，故fR横≈fS，即横向多普勒效应很不明显，难于观测到．

3 斜向多普勒效应

下面讨论更为一般的多普勒效应——斜向多普勒效应．如图3所示，观测者R静止，以R处为原点O，建立坐标系xOy，简称R系.

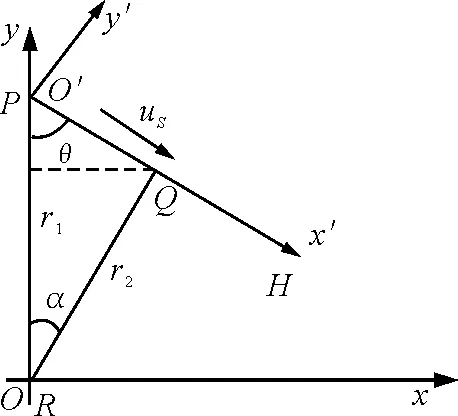
图3

在y=r1的P处，有一以速度uS沿PH方向运动的波源S，PH与PR成θ角．以波源S处为原点O′，建立坐标系x′O′y′,简称S系，x′轴与PH重合，t=0时刻波源刚好在P处，假设(7)式仍然成立，但此时沿y轴负方向传给观测者的波在S系上的伽利略相对波速为(vφ-uScosθ)，于是得

及

vφTR=λ0

由此得

(14)

(14)式的正确性，亦可仿照前述的方法加以验证．设在R系上，观测者观测到的圆频率为ωR；在S系上，波源发射波的圆频率为ωS，自t=0时刻开始，波源由R系的P处沿PH方向(即S系的x′轴正方向)以速度uS运动，经一微小时间Δt运动到Q处，则观测者接收到来自P、Q两处的波振动，其位相差为

因Δt很小，α角很小，所以有

故

而在S系上看，波源在P、Q两处发射的波振动位相差为Δφ′=ωSΔt′(Δt′为在S系上观测的时间)，根据位相不变原理得Δφ=Δφ′，即

根据洛伦兹变换，有

并代入上式得

令ωR=2πfR，ωS=2πfS，于是得

此式与(14)式一致.

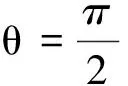
综上所述，知(7)式既适用于纵向也适用于横向多普勒效应.多普勒效应的这一最简规律可表述为：在任一惯性系里，伽利略变换下的相对波长等于洛伦兹变换下的收缩波长．