此题还一个解
——对《正确使用平均值》一文的补充
2011-08-16 09:46:44姜付锦
物理通报 2011年7期
姜付锦
(武汉市黄陂区第一中学 湖北武汉 430030)
《物理通报》2010年第6期一篇文章《正确使用平均值》[1]中,例题1的参考解答是利用动量与能量的观点来研究的.但笔者认为此题还有一个解,分析如下.文中如有不当之处还请各位批评指正.
【题目】
质量为m长为L的平板小车,放在光滑的水平面上,左端靠近一固定轻弹簧的自由端(不连接).用一水平外力缓缓推动小车将弹簧压缩,当弹簧被压缩了x0时,将小车用销钉固定,此时弹簧的弹性势能为Ep.现将一质量也为m、与小车之间动摩擦因数为μ的金属块放在小车的右端,如图1所示.突然去掉固定销钉,小车被弹簧推动,同时金属块与小车开始发生相对滑动,小车离开弹簧后两者又继续相对滑动了一段时间,最终金属块恰好停在了小车的最左端.求:
(1)金属块相对小车停止相对滑动时两者速度的大小;
(2)从拔掉销钉到小车离开弹簧的时间.
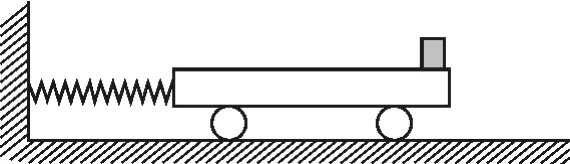
图1
原解:
(1)设两者最后速度为v,根据能量守恒有
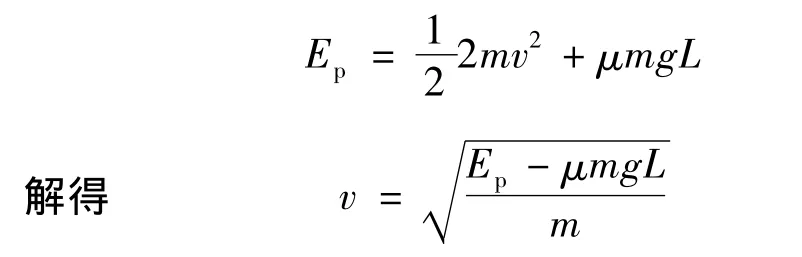
(2)弹簧恢复原长时,小车与弹簧分离.设从运动到分离所用时间为t,分离时车的速度为v1,金属块的速度为v2,此过程弹簧对小车做功等于Ep
对金属块 μmgt=mv2
对整体,小车离开弹簧后,系统动量守恒
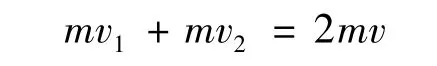
联立以上各式可得
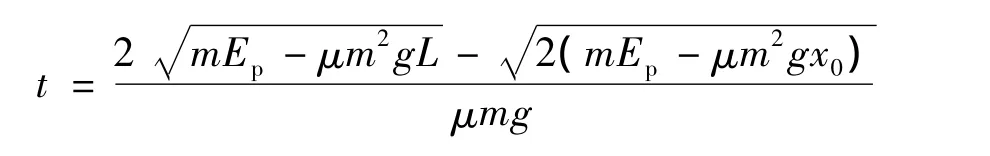
另一个解
小车在水平方向所受的外力有弹簧的弹力和与金属块的摩擦力,其中弹力是正比于弹簧形变量,而摩擦力为f=μmg,可以把摩擦力等效成重力即
mg'=μmg,从而把小车的运动等效为竖直方向上的弹簧振子的运动.
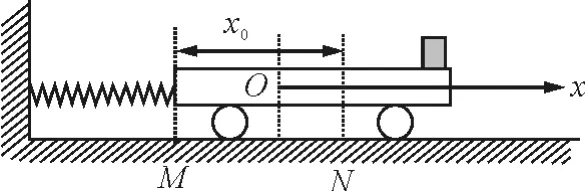
图2
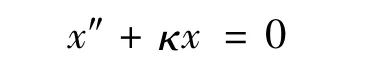
初始条件x(0)=-A,x'(0)=0.
此方程的通解为
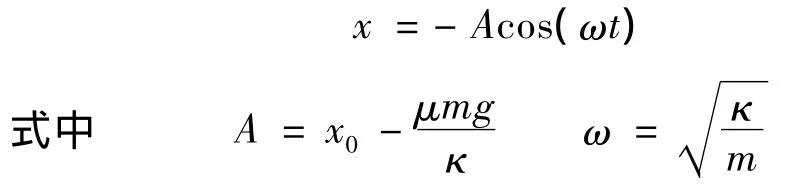
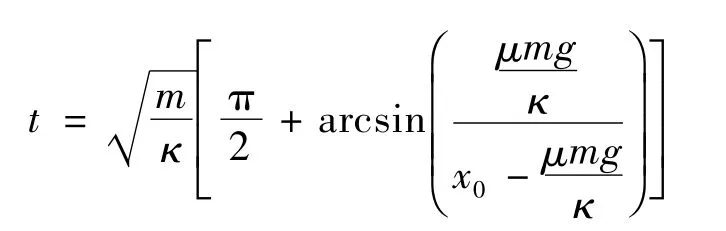
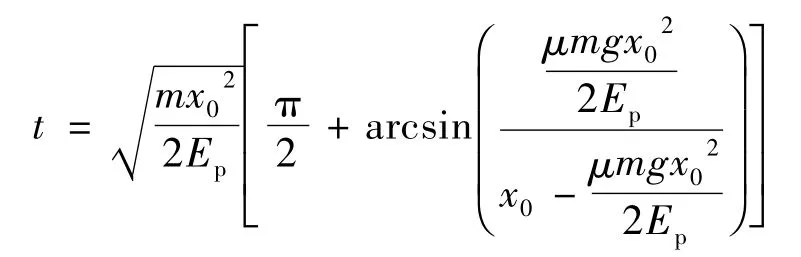
通过这个例子可以认识到对于有关弹簧振子的题目,既可以从动量与能量的观点来研究,还可以运用简谐振动的知识来研究,二者是等效的.
猜你喜欢
高中数理化(2024年8期)2024-04-24 05:21:33
中国铁路(2022年8期)2022-09-22 02:41:24
轻兵器(2022年3期)2022-03-21 08:37:28
中学生数理化·自主招生(2021年8期)2021-05-30 10:48:04
中学生数理化(高中版.高考理化)(2020年9期)2020-10-27 02:30:46
中学生数理化(高中版.高考数学)(2020年1期)2020-02-20 13:23:44
机械制造文摘(焊接分册)(2018年3期)2018-08-08 02:11:02
数学物理学报(2018年1期)2018-03-26 08:16:58
电测与仪表(2016年18期)2016-04-11 11:30:30
物理实验(2015年10期)2015-02-28 17:36:55

