基于约束条件的三次NURBS曲线插值研究

陈绍平，何精雄，李 真

(武汉理工大学 理学院，湖北 武汉 430070)

1 引言

非均匀有理B样条(NURBS)[1]是几何造型的一个十分有用的工具，在计算机辅助设计和辅助制造集成系统中都得到广泛的应用.又因为它具有局部性、凸包性、仿射与透视不变性、参数连续性等优良性质，因此NURBS方法受到工程界人士的广泛的重视[2].在实际应用中，人们可以利用三次NURBS曲线插值方法得到一条理想的光顺曲线，比如船舶型线设计就用到此方法.因此研究三次NURBS曲线插值方法具有非常重要的实际意义，它不仅提供生成曲线的方法，而且为工程设计人员提供了理论依据.

2 基于约束条件下的三次NURBS曲线插值

2.1 NURBS曲线

由于NURBS方法是一种可以统一表示初等曲线曲面和自由型曲线曲面的方法，一旦节点矢量、控制顶点和权因子被确定之后，NUBRS曲线和曲面的形状也就唯一确定了.比如一条K次NUBRS曲线可以表示为：

其中，ωi(i=0,1,…,n)称为权因子，ω0,ωn>0,wi≥0， 以防分母为零；di(i=0，1，2，…，n)为控制顶点.Ni,k(u)是由节点矢量U=[u0,u1,…,un+k+1]决定的K次规范B样条基函数.B样条基函数的de Boor-Cox递推公式如下：

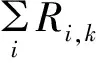
2. 2 某两点具有曲率限制的NURBS曲线插值

其中di=ui+1-ui，Qi为控制点.

下面根据任意两点曲率限制推导控制点所对应的方程，由于非均匀B样条曲线的各节点处有：

aiQi-1+biQi+ciQi+1=ei;i=2,3,…,n

(3)

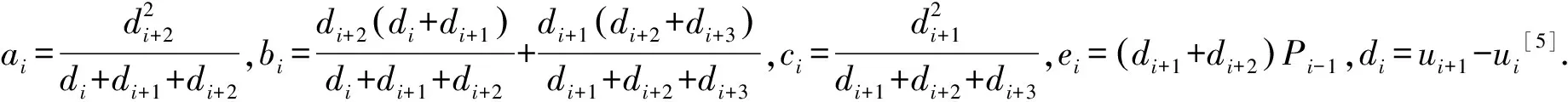
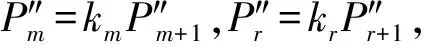
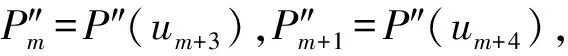
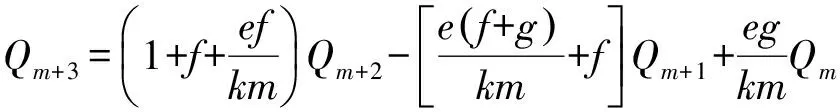
(4)

又由式(3)得：

am+2Qm+1+bm+2Qm+2+cm+3Qm+3=em+2

(5)

故把式(4)代入式(5)得：

(6)

又由式(3)得：

am+1Qm+bm+1Qm+1+cm+1Qm+2=em+1

(7)

联立式(6)、(7)消去Qm得：

(8)

在式(8)中令Qm+1的系数为Am+1，Qm+2的系数为Bm+1，令右边式子为Em+1,得：

Am+1Qm+1+Bm+1Qm+2=Em+1

(9)

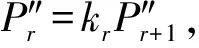
故在关于控制点的方程组(3)中，又可以增加两个方程，得到关于控制点的矩阵方程为:

由于其系数矩阵可逆，而且有n+1个未知数，n+1个方程，故可求出唯一的一组控制点[6].

2.3 某一点只有切矢约束，另一点只有曲率限制的NURBS曲线插值

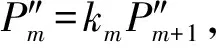
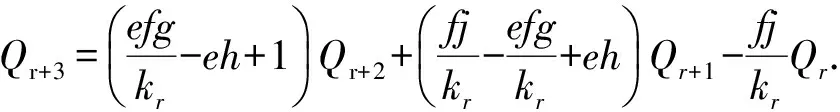
(10)

又由于ar+1Qr+br+1Qr+1+cr+1Qr+2=er+1

(11)

ar+2Qr+1+br+2Qr+2+cr+2Qr+3=er+2

(12)

把式(10)代入式(12)并与式(11)联立，消去Qr得：

(13)

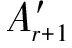
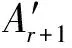
(14)

将式(9)和式(14)都代入节点方程组(3)中也可以得到n+1个方程的方程组，即：

可求出唯一一组控制点Qi,i=1,2,…,n+1,对于NURBS曲线，只要在该方程组中，将Qi改成带权控制顶点Di，再取其在w=1超平面上的投影即可求出Qi.

3 结束

本文的方法能够使三次NURBS曲线更好的满足操作者的需要，操作者只需改变相应的曲率参数和切矢参数就可以很好的控制曲线的形状，从而得到所需要的曲线.

[1] Piegl L.On NURBS: A Survey[J].IEEE CG&A,1991：55-71.

[2] 李东，汪希龄.应用曲率参数的B样条曲线插值方法[J].船舶工程，1994(3)：55-58.

[3] 施法中.计算机辅助几何设计与非均匀有理B样条[M].北京：北京航空航天大学出版社，1994：228-238.

[4] 李强，席光，王尚锦.NURBS曲线插值的实现方法与探讨[J].计算机工程与应用，1999(7)：24-26.

[5] 苏晓红，李东，王宇颖.基于曲率参数的NURBS曲线插值[J].哈尔滨工业大学学报，2001,33(1):108-111.

[6] 秦开怀，孙家广，范刚.三次NURBS曲线的插值方法[J].计算机辅助设计与图形学学报，1993,5(3)：179-183.

[7] Les A Piegl,Wayne Tiller.Curve Interpolation with Arbitrary End Derivatives[J].Engineering with Computers，2000,16：73-79.

[8] Les A Piegl,Khairan Rajab,Volha Smarodzinana.Curve interpolation with directional constraints for engineering design[J].Engineering with Computers，2008,24：79-85.