特征系统实现算法中的噪声问题研究*

李 萍,王树青,李华军

(中国海洋大学工程学院,山东青岛266100)

特征系统实现算法中的噪声问题研究*

李 萍1,王树青2,李华军3

(中国海洋大学工程学院,山东青岛266100)

研究特征系统实现算法在模态识别过程中的噪声处理问题。特征系统实现算法为目前土木工程领域应用较为广泛的一种模态识别法。在处理实测数据时,特征系统实现算法将实测数据分解为结构真实信号和噪声信号,从而将噪声消除。分块Hankel矩阵的维数对信噪分离过程影响很大。提出当分块Hankel矩阵的分块行与分块列数接近时,真实和噪声信号可以最好的分离。通过在实测信号里添加噪声(产生噪声-噪声信号),将实测信号和噪声-噪声信号识别的结果进行比较,提出了1种验证识别模态参数是否为结构真实模态的检验方法。本文应用导管架平台实例来验证提出方法的适用性。结果表明,当分块Hankel矩阵的分块行与分块列数接近时,真实和噪声信号能够有效地分离,此时添加的噪声主要影响噪声信号部分。由实测信号和噪声-噪声信号识别的模态参数非常吻合。

模态参数识别;特征系统实现算法;噪声;模型阶数

模态参数识别是通过结构的动态特性试验数据,来估计结构模态参数的过程[1-2]。模态参数识别结果的准确性直接影响到结构物有限元模型修正和损伤检测工作的进行[1,3]。参数识别方法分频域法和时域法2类。时域法是1970年代随着计算机技术迅速发展起来的,先后经历了单输入单输出(SISO)、单输入多输出(SIMO)、多输入多输出(M IMO)3个阶段。

特征系统实现算法(Eigensystem Realization A lgorithm,ERA)是美国NASA的Langley研究中心于1984年在最小实现理论基础上提出来的[4],属于M IMO时域整体模态参数识别方法。该方法源于控制理论中Ho-Kalman的最小实现理论[5],利用脉冲响应数据,采用奇异值分解(SVD),求得模态参数。目前在国外航空航天领域应用广泛。

特征系统实现算法通过M arkov参数(如:脉冲响应数据)来组建分块Hankel矩阵,并以此矩阵作为离散时间状态模型[6]实现的基础。通过最小实现理论,ERA方法可用于实测信号的模态参数识别。ERA算法的实质是:将实测信号分解为真实信号和噪声信号,并借助于模态置信度(MAC)和模态奇异值(M SV)来区分真实和噪声模态[7]。其中,分块Hankel矩阵秩(即模型阶数)的确定对能否将真实信号和噪声信号有效地分离非常关键。周等[8]提出了利用奇异值差值法进行模型定阶,该方法具有直观,无需进行反复试算的特点。Hu[9]等,Peeters[10]等,M isra[11]等利用了奇异值分解法进行模型定阶。目前的噪声处理方法大多对信号进行降噪预处理,得到消噪信号后再进行模态识别。林[12]等提出了利用小波去噪方法对脉冲响应信号进行处理。Zhang[13-14]利用相关滤波对测量数据进行预处理,有效地提高了识别精度。本文研究ERA方法中的噪声处理问题。区别于以往对实测信号进行降噪预处理的方法,本文研究模态分析过程中如何将真实信号和噪声信号有效地分离。Hankel矩阵维数对其信噪分离过程很关键。如果矩阵的维数选择不佳,可能导致真实和噪声信号不能很好地分离,从而影响模态参数识别的准确性。

本文提出了确定最佳分块Hankel矩阵的方法。通过对此矩阵最佳维数的确定,可以使真实信号和噪声信号有效分离,保证识别模态的准确性。本文还提出验证识别的模态参数鲁棒性和准确性的方法。此方法通过在实测信号中添加噪声,称之为噪声—噪声信号,并比较由实测信号和噪声—噪声信号识别的模态参数的符合性,来确定识别模态是否为真实模态。文中借助导管架平台模型检验所提出方法的有效性。

1 特征系统实现算法(ERA)

时不变系统的连续时间状态方程可表示为:

其中,x∈Rn,u∈Rr,y∈Rm分别为状态向量,输入向量和输出向量;n=2M,为模型阶数;M为系统参与模态数;r和m分别为输入和输出数量。常数矩阵Ac,Bc,C和D代表线性系统的内部关系。

离散时间状态空间模型可表示为:

其中,k代表某个时刻,常数矩阵A和B可由Ac,Bc得到。

当输入为脉冲激励时,输出脉冲响应数据Yk∈Rm×r可表示为:

公式(3)中的常数矩阵序列又称为M arkov参数。ERA系统实现为通过公式(3)中的M arkov参数来求解公式(2)中的矩阵组[A,B,C]的过程。同一个输入输出系统可有多个实现来表示。其中最小实现指状态矩阵A的维数最小时对应的模型。

假设状态矩阵A线性独立的特征向量为(Ψ1,Ψ2,…,Ψn),对应的特征值为(λ1,λ2,…,λn)。定义Λ为特征值对角矩阵,Ψ为特征向量矩阵。矩阵组[A,B,C]的实现过程可转换为矩阵组[Λ,Ψ-1B,CΨ]。对角矩阵Λ中包含了模态阻尼比和阻尼频率信息;矩阵Ψ-1B包含初始模态幅值信息;矩阵CΨ包含传感器位置处的模态振型信息。结构的所有模态参数可由矩阵组[Λ,Ψ-1B,CΨ]来获得。在将特征值对角阵Λ通过Λc=ln(Λ)/Δt转换到连续时间域后,其实部和虚部分别对应模态阻尼比和阻尼频率。这里需要指出,从数学角度,当状态矩阵A的特征值存在重根时,其对应的模态振型并不一定唯一。重根对应的2个模态振型的任一组合均可构成一个新的振型[6]。在工程领域,结构频率可能非常接近,出现重根(相同频率)的几率很小。

系统实现是通过公式(3)中的Markov参数来组建维数为αm×βr的分块Hankel矩阵开始的:

其中,α为分块行数;β为分块列数。

1.1 模型定阶

模型阶数n的选择对模态参数识别精度影响很大。目前,模型定阶已成为模态参数识别领域的最为重要的问题。这里模型定阶方法是通过矩阵H(0)的秩来确定n的值[9,15]。

当k=1时,可以得到

n为模型阶数,当αm≥n且βr≥n时,矩阵H(0)的秩理论上为n。

目前常用确定矩阵秩的方法为奇异值分解法。通过对矩阵H(0)进行奇异值分解(SVD),

其中,矩阵R∈Rαm×αm和S∈Rβr×βr为正交矩阵,矩阵Σ∈Rαm×βr为对角矩阵,其对角元素为降序排列的奇异值。理论上,超出矩阵秩的奇异值应当为0,即Σ可分解为

其中,Σn=diag[σ1,σ2,…,σn]。对实测信号,由于噪声影响,超出矩阵秩的奇异值并不等于0,而会变得很小。这里采用的确定模型阶数的方法为首先将奇异值根据第一个奇异值σ1进行归一化处理,然后划出归一化奇异值图,当奇异值图趋近于水平时,对应的奇异值个数即为矩阵的秩[9]。

1.2 系统最小实现

当k=2时,公式(4)为

定义 Oi为阶数i的空矩阵,Ii为阶数i的单位阵,则以下矩阵组

为一最小实现。其中,Rn和Sn分别为矩阵R和S的前n列。^代表估算值。当测量信号噪声很小时,状态矩阵^A的秩为n,即系统的阶数。

1.3 模态奇异值(M SV)

M SV是量测识别的各阶模态对实测响应信号贡献大小的一种方法。M SV的计算公式如下:

其中,

2 噪声消除法

假设某实测信号有M个参与模态,其对应的分块Hankel矩阵H可分解为2部分:

其中,S和N分别代表真实信号和噪声信号对应的矩阵。信噪分离过程就是基于H(0)得到S。在将矩阵H(0)逼近到S时,通常应用最小化H(0)和S的差别的Frobenius范数的方法,即:‖H(0)-S‖2最小。矩阵S可由矩阵H(0)通过奇异值截断得到,这种方法称为截断奇异值分解法(TSVD)或者Eckart-Young方法[16]。注意,矩阵S不具备原有矩阵H(0)的分块Hankel结构。此外,本方法不需迭代。

特征系统实现算法噪声处理与分块行数α和分块列数β的选取方式关系很大。ERA法识别模态参数的准确度主要依赖于能否将S和N有效地分离。1个最直接的想法是使H(0)的第n个奇异值σn与第n+1个奇异值σn+1的差别越大越好(n=2M),即由归一化奇异值图观察到奇异值σn和σn+1处有一个突降。这里取α和β最接近的情况,这时矩阵H(0)的维数最大。假设每个信号只采用99个信号点,满足α+β-1=99的情况下,则(α,β)的最优取法为(50,50),此时矩阵H(0)维数最大,且奇异值数p也最多(p=min(αm,βr))。当参与S的模型阶数为2M时,参与N的组成个数为p-2M,这里假设所有的p-2M个组成均为噪声。

3 模型实验

3.1 海洋导管架平台模型概述

采用某一海洋导管架平台模型来验证提出的噪声处理方法的有效性,见图1。平台采用钢材,甲板尺寸为0.6 m×0.3 m,厚度为0.01 m;平台高度1.7 m,4条腿斜率均为10∶1,采用直径D=0.025 m,厚度t=2.5 mm的钢管;导管架设3层水平横撑,分别位于1.35,0.9和0.5 m处,在0.9和0.5 m处设竖向斜撑。水平横撑和斜撑的尺寸均采用直径D=0.016 m,厚度1.5 mm的钢管。

平台上共布设32个传感器(4层,每层8个传感器),由于实际海洋平台通常把传感器布设在水面以上,这里只采用平台上层的8个传感器进行分析(见图1),x和y向传感器各4个。分别施加脉冲激励于平台甲板的中间和边缘的x和y方向(见图1),可获得共32个测量信号,采样频率为500 Hz(Δt=0.002 s)。同时,利用ANSYS建立有限元模型,计算得到前8阶模态频率(不包括刚体模态)见表1。

图1 实验室内导管架平台模型Fig.1 Test jacket-type p latform in the lab

表1 有限元得到的前八阶模态Table 1 Modal p roperties of the first eight modes of the FEmodel fo r a jacket-type offsho re p latform

对每个实测信号,只取200个测点进行分析,见图2。为了检验识别模态的真实性,对测量信号后期添加噪声,产生噪声—噪声信号,进而比较测量信号和噪声—噪声信号识别的模态参数的符合性。如果他们相一致,则表明添加的噪声没有影响真实信号,则测量信号中的噪声对其识别的准确性也影响不大。假设如下:如果S和N能有效地分离开来,则添加的噪声将主要影响N,因而基于S的模态识别变化会非常小。噪声—噪声信号的模拟是通过在测量信号基础上添加高斯白噪声得到的。添加噪声的概率密度函数满足正态分布,同时它的功率谱密度函数理论上是常数。噪声水平通过一个百分比来定量描述,该百分比定义为白噪声的标准差和测量信号的标准差之比。当噪声水平很低时,其对矩阵秩的影响并不明显,只有噪声达到一定水平时,矩阵的秩才会发生明显变化。同时,图2中还给出的是某信号添加的15%噪声。图3为图2中给出的某15%噪声的功率谱密度函数。由图3可知,其功率谱密度函数大体在某常数值附近波动。

图2 某实测信号截取的200个测点和添加的15%噪声Fig.2 An examp le of themeasured and injected 15%noise signal

图3 图2中给出的某15%噪声的功率谱密度函数Fig.3 Power spectra density of injected 15%noise in Fig.2

3.2 模型阶数确定

首先,研究噪声对单个信号模型阶数的影响。对于图2给出的单个信号实例,其测量信号和含15%的噪声—噪声信号对应的H(0)(取α=100,β=100)矩阵的归一化奇异值曲线见图4,每个奇异值均由第一个(最大)奇异值归一化所得。从图4可知,对于单一信号,添加的15%噪声对奇异值影响很大,其影响已从第4个奇异值开始。

对实测的32个信号,采用前199个测点来组建分块Hankel矩阵H(0)。可通过H(0)秩的大小来获得参与模态数量,理论上H(0)的秩(即模型阶数)为模态数的2倍[17]。

图4 某实测信号和含15%噪声-噪声信号对应的归一化奇异值图Fig.4 Normalized singular values of the Hankel matrix from one signal

这里研究矩阵H(0)的2种情况:(1)α=100,β=100,矩阵H(0)∈R800×400;(2)α=3,β=197,矩阵H(0)R24×788。2种情况对应的归一化奇异值曲线见图5。在这里当归一化奇异值曲线突降接近水平时,认为此奇异值处对应分块Hankel矩阵的秩。从图5可以观察,对于情况一,可以明显观察到在第8个奇异值处曲线有明显的突降,而对于情况二则没有此现象。因此,可以从情况一中得出矩阵的秩为8。对于第二种情况,采用相同的模型阶数。

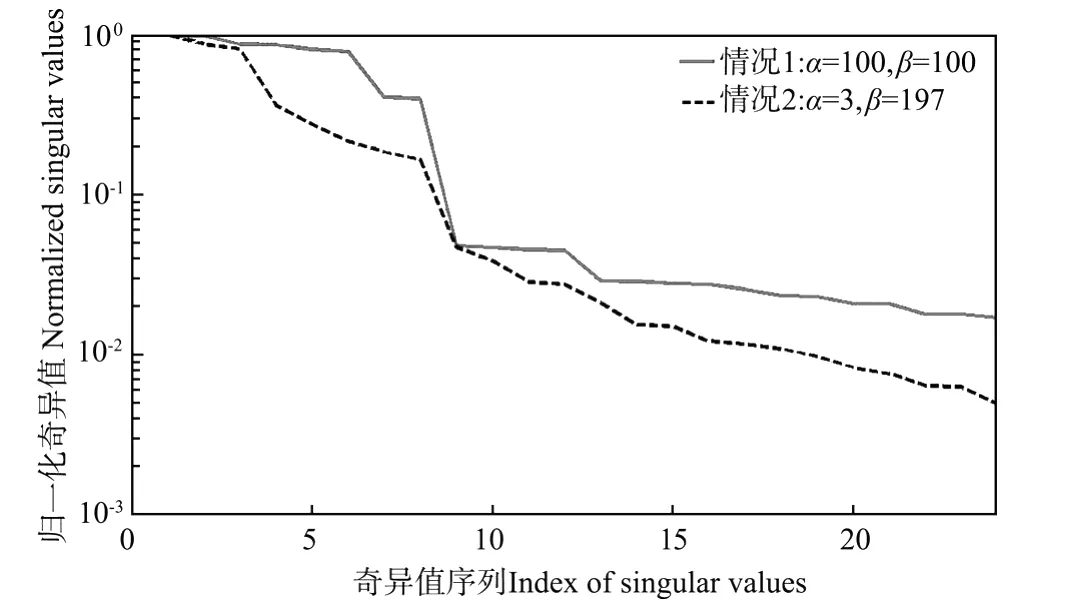
图5 2种情况下实测信号对应的归一化奇异值图Fig.5 Normalized singular values of the block Hankelmatrices from 128 signals

在32个测量信号上分别添加5%和15%的白噪声来产生噪声—噪声信号。2种情况下对应的测量和噪声—噪声信号的归一化奇异值曲线分别见图6和图7。

从图6可知,对第一种情况,测量信号、含5%和15%噪声-噪声信号对应矩阵的秩皆为8。且添加的噪声绝大部分影响第8个之后的奇异值,对前8个奇异值影响非常小。而对于情况二(见图7),添加噪声主要影响第8个之后的奇异值,但对前8个奇异值(5～8个)也有影响,由于不能由图7明确判定矩阵的秩,这里采用与情况一相同的模型阶数。

图6 测量和噪声—噪声信号对应的归一化奇异值图(情况一)Fig.6 No rmalized singular valuesof the block Hankelmatrices for case 1

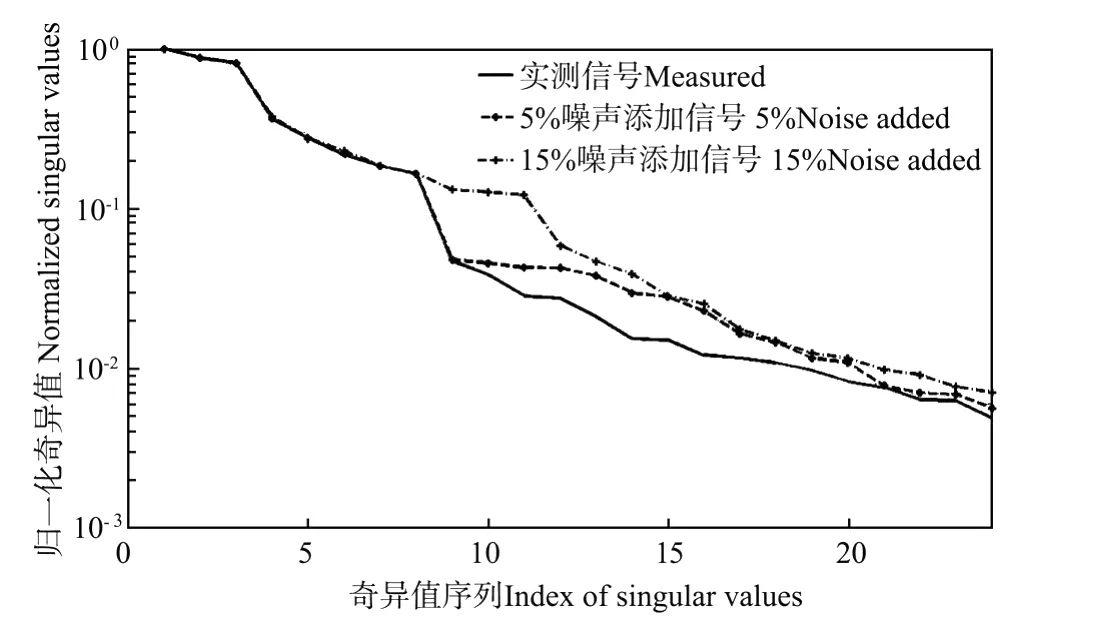
图7 测量和噪声—噪声信号对应的归一化奇异值图(情况二)Fig.7 Normalized singular values of the block Hankelmatrices for case 2

表2 测量信号和噪声—噪声信号识别的模态频率(情况一)Table 2 Estimated frequencies from measured,5%-noise and 15%-noise added signals(Case 1)

表3 测量信号和噪声—噪声信号识别的模态频率(情况二)Table 3 Estimated frequencies f rom measured,5%-noise and 15%-noise added signals(Case 2)

3.3 模态参数识别

在确定模型阶数之后,根据公式(9)可求得一最小实现,进而求得模态参数。表2和表3中分别为两种情况下由测量信号、含5%和15%噪声-噪声信号识别的模态频率。对比表2和表3可知,情况一识别的模态频率在添加噪声前后差别很小,相对误差均小于0.005%,而情况二识别频率的最大相对误差为0.632%。此外,情况一的识别频率与有限元得出的频率也更接近。

表4和5中分别为2种情况下由测量信号、含5%和15%噪声-噪声信号识别的模态阻尼比。由表4可知,情况一中识别的阻尼比相对误差最大处为第4阶识别模态,为10%。对比情况二(表5),其阻尼比最大相对误差为990.476%,为第四阶模态。可知当α和β取值接近,即当矩阵H(0)分块行和列的数目相近时,识别结果明显提高,尤其是阻尼比,此时噪声信号已被有效地分离并剔除,识别结果比较准确。

表4 测量信号和噪声—噪声信号识别的模态阻尼比(情况一)Table 4 Estimated damping ratios from measured,5%-noise and 15%-noise added signals(Case 1)

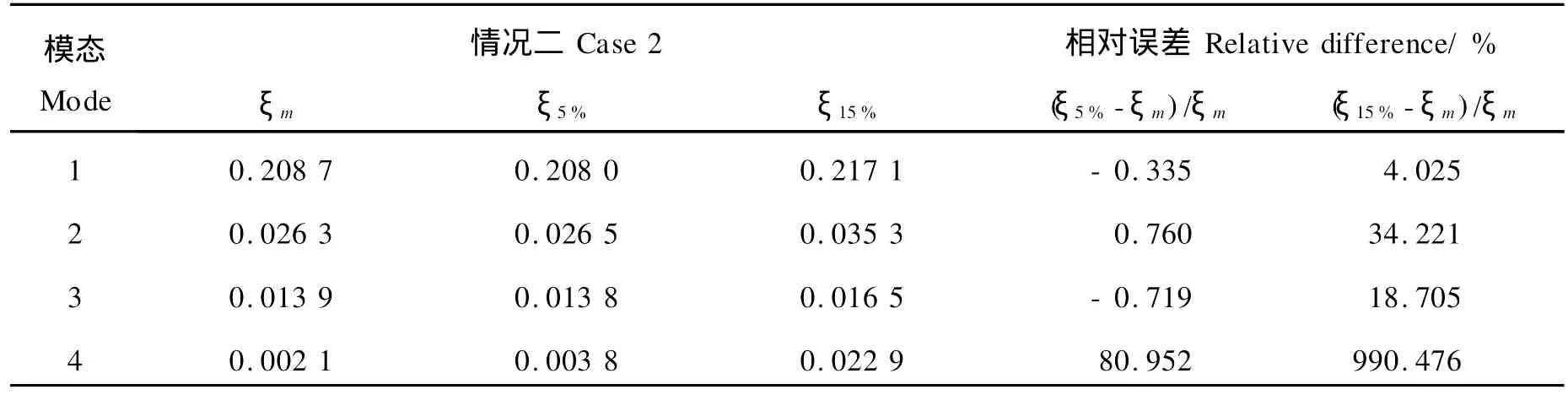
表5 测量信号和噪声—噪声信号识别的模态阻尼比(情况二)Table 5 Estimated damping ratios from measured,5%-noise and 15%-noise added signals(Case 2)

表6和7分别为2种情况下由测量信号、含5%和15%噪声-噪声信号识别的模态奇异值(M SV)。M SV是各识别模态对测量信号贡献大小的量度。由表可见,情况一(见表6)识别的M SV值一致性要比情况二(见表7)的好。此外,由表6和表7可知,第3阶识别模态贡献最大,第4阶识别模态贡献最小。

表6 测量信号和噪声—噪声信号识别的M SV值(情况一)Table 6 Estimated MSV from measured,5%-noise and 15%-noise added signals(Case 1)

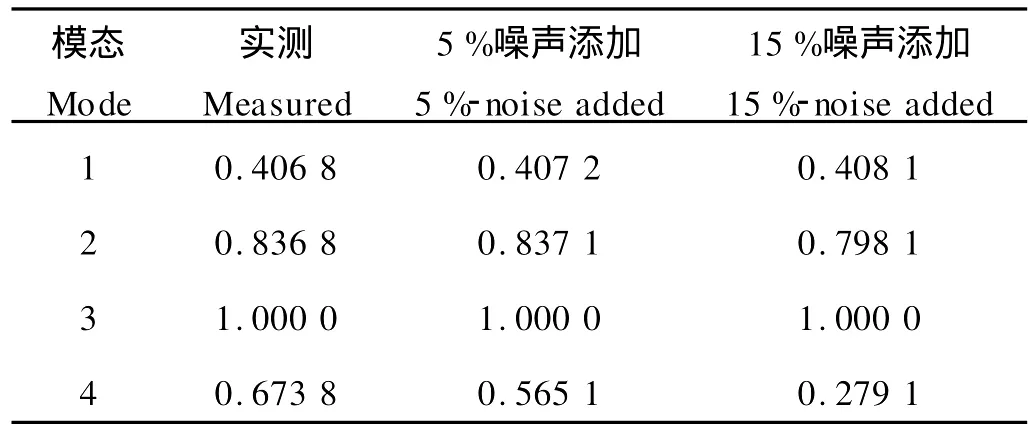
表7 测量信号和噪声—噪声信号识别的M SV值(情况二)Table 7 Estimated MSV from measured,5%-noise and 15%-noise added signals(Case 2)

4 结语

针对特征系统实现算法,本文提出了基于分块Hankel矩阵维数选择来进行信噪分离,从而将噪声剔除的方法。通过采取分块行和列的数目最接近的Hankel矩阵结构,识别的模态参数准确性有明显提高,尤其是识别阻尼比有明显改善。通过在测量信号中添加噪声,并比较测量信号和噪声—噪声信号识别模态参数的一致性,来判别识别模态是否为结构真实模态。物理模型试验结果表明,通过选择最佳的分块Hankel矩阵维数,可以有效地将真实信号和噪声信号分离,提高识别精度。

[1] Ew ins D J,Modal Testing:Theory,Practice and Applications[M],2nd Edition.Baldock,Hertfordshire,England:Research Studies Press,2000.

[2] Maia N,Silva J,He J,et al.Theoretical and Experimental Modal A-nalysis[M].Taunton,Somerset,England:Research Studies Press,1997.

[3] Friswell M I,Mottershead J E,Finite Element Model Updating in Structural Dynamics[M].1st edition,Nethelands:Kluwer Acadamic Publishers,Sp ringer,1995.

[4] Juang J N,Pappa R S,An eigensystem realization algo rithm fo r modal parameter identification and model reduction[J].Journal of Guidance,Control,and Dynamics.1985,8(5):239-260.

[5] Ho B L,Kalman R E,Effective construction of linear state variablemodels from input/output data[C].∥Proceedingsof the 3rd Annual A llerton Conference on Circuit and System Theory.U rbana:university of Illinois,1966,14:545-548.

[6] Juang J N.Applied system identification[M].1st Edition:USA:Prentice-Hall Inc.,1994.

[7] Juang J N,Pappa R.S,Effectsof noise onmodal parameters identified by the eigensystem realization algorithm[J].Journal of Guidance,Control,and Dynamics.1986,9(3):294-303.

[8] 周帮友,胡邵全,杜强,特征系统实现算法中的模型定阶方法研究[J].科学技术与工程,2009,9(10):2715-2716.

[9] Hu SL J,Bao X X,Li H J.Model order determination and noise removal for modal parameter estimation[J].Mechanical Systems and Signal Processing,2010,24(6):1605-1620.

[10] Peeters B,De Roeck G.Reference-based stochastic subspace identification for output-only modal analysis[J].Mechanical Systems and Signal Processing,1999,13(6):855-878.

[11] Misra P.Nikolaou M,Input design for model order determination in subspace identification[J].AlChEJournal,2003,49(8):2124-2132.

[12] 林贵斌,陆秋海,郭铁能.特征系统实现算法中的小波去噪方法研究[J].工程力学,2004,21(6):91-96.

[13] Zhang L M.A polyreference frequency domain method formodal parameter identification[C].Ohio:ASME Design Engineering Division Conference and Exbit on Mechanical Vibration and Noise OH IO,1985,85-DET-106.

[14] Zhang L M,An imp roved time domain polyreference method for modal identification[J].Mechanical Systems and Signal Process-ing,1987,1(4):399-413.

[15] Sanliturk K Y,Cakar O,Noise elimination from measured frequency response functions[J],Mechanical Systems and Signal Processing,2005,19(3):615-631.

[16] Eckart C,Young G,The approximation of onematrix by another of lower rank[J].Psychometrika,1936,1(3):211-218.

[17] Li P,Li H J,Hu SL J.Estimating modal parameters from free vibration response of jacket-type platforms[C].China:Proceedings of the Twentieth International Offshore and Polar Engineering Conference,2010:20-25.

Noise Handling of the Eigensystem Realization Algorithm

L IPing1,WANG Shu-Qing2,L IHua-Jun3
(College of Engineering,Ocean University of China,Qingdao 266100,China)

In dealing with noisy measurement data,the Eigensystem Realization Algo rithm(ERA)partitions the realized model into signal and noise portions so that the noise portion can be disregarded.A critical issue is the determination of the dimensions of the block Hankelmatrix.We show that the signal and noise matrices can be better separated when the number of block-row sand number of block-columns of the corresponding block Hankelmatrix are chosen to be close to each other.We propose a verification procedure to justify that the estimated modal parameters are noise insensitive and thus indeed associated with the true system.The procedure involves artificially injecting random noise into the measured signals to create noisy-noisy signals,then comparing the identification results obtained respectively from the measured and noisy-noisy signals.Using experimental data collected from a jacket-type p latform,we demonstrate that signal and noise portions can be p roperly separated w hile the number of the block-rows and number of block-columns are close.

model parameters identification;eigensystem realization algorithm;noise;model order

TP273

A

1672-5174(2011)7/8-176-07

国家自然科学基金项目(51079134),重大国际合作研究项目(51010009)资助

2011-01-08;

2011-4-14

李 萍(1983-),女,博士生。E-mail:lipingljk@gmail.com

责任编辑 陈呈超