主能量脉冲反褶积*
李金山,姜秀萍,王修田**
(中国海洋大学1.海洋地球科学学院;2.海底科学与探测技术教育部重点实验室,山东青岛266100)
主能量脉冲反褶积*
李金山1,2,姜秀萍1,2,王修田1,2**
(中国海洋大学1.海洋地球科学学院;2.海底科学与探测技术教育部重点实验室,山东青岛266100)
本文提出的主能量脉冲反褶积方法,旨在保持原反褶积相位特性的同时将有效频带拓宽为期望输出的主能量谱,以期获得更为可靠的地震分辨率。其首先根据地震波的有效频带范围设计出期望输出的主能量谱,然后通过主能量谱滤波获得主能量信号,并以其为输入求取初始的反褶积因子,再在保持初始反褶积因子相位特性的前提下以主能量谱为期望的振幅谱,求取1个优化的反褶积因子,最后即可通过褶积运算获得期望输出的地震信号。
反褶积;地震有效频带;主能量谱;白噪系数
获得高分辨率的地震剖面一直是地球物理学家们追寻的目标,反褶积技术是提高分辨率的重要手段之一,其基本目的是压缩子波,提高地震资料的分辨率,进而更有效地辨别地下反射界面[1]。长期以来,人们提出了多种反褶积技术方法[1-6],例如最小平方反褶积、预测反褶积、最小熵反褶积、最大熵反褶积以及同态反褶积等等。最小平方反褶积是目前油气地震勘探中常用的反褶积方法,而脉冲反褶积是期望输出为零延迟尖脉冲时的最小平方反褶积,其取得较好效果的前提条件是地震子波为最小相位的且反射系数序列与随机噪音均为白噪。此外,对整个区域来讲还应满足地表一致性条件[7]。当实际情况越满足假设条件时,反褶积的效果就越好,反之效果就差。如果地震记录中的噪音比较严重,该方法只能通过加大白噪系数的方式来折衷反褶积后地震记录的信噪比和分辨率,难以达到理想的效果,且白噪系数大小没有1个直观的选取标准,只能通过实验效果来确定。
本文在前人工作的基础上,提出了主能量脉冲反褶积方法,其基本思想是先在地震主能量(即有效波的主频带范围)内求取初始的反褶积算子,再在保持原反褶积相位特性的同时按地震波的有效频带范围拓宽频谱,合成最优的反褶积算子。其中地震波的主频带范围可通过对地震记录的频谱分析和频率扫描来确定。众所周知,反褶积或反滤波的基本目的是在时间域压缩子波,对应于频率域即是拓宽频谱,而只有在地震有效波的主频带范围内拓宽频谱才是有意义的反褶积。因此,通过主能量脉冲反褶积压缩子波后的地震记录更具有可靠性。由于主能量脉冲反褶积是在地震波的有效频带范围内拓宽频谱,即使在噪音比较严重的情况下,其仍可取很小的白噪系数而获得较好的反褶积效果。
1 常规脉冲反褶积的参数分析
常规的脉冲反褶积一般是在时间域内实现的,其处理效果的好坏一般也是根据反褶积后的地震记录的质量来检验。根据脉冲反褶积的(可参阅文献[8]等)基本原理和实现方法,相关时窗长度、反褶积因子长度与白噪系数等3个参数的取值大小将直接影响着脉冲反褶积的处理效果。
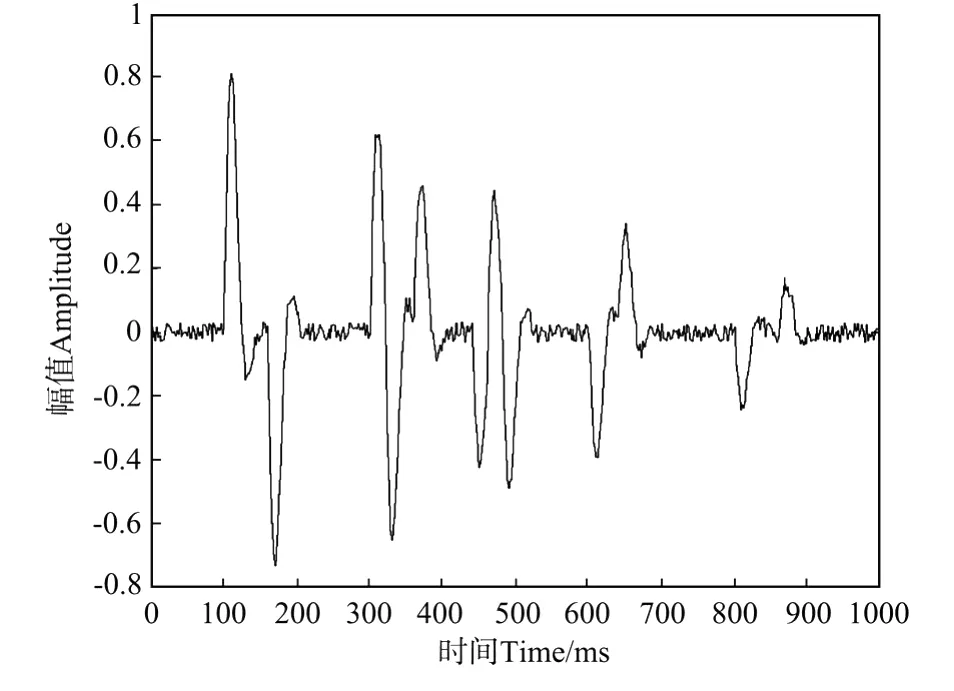
图1 原始地震记录Fig.1 The original seismic record
尽管当相关时窗和反褶积因子的长度取值过小时会使得脉冲反褶积的处理效果变差,但在实际处理中恰当地选取这两个参量还是相对容易的,即相关时窗和反褶积因子的长度足够长即可。参数选择的主要的难点是白噪系数的取值。为了能直观分析白噪系数的大小对反褶积效果的影响,本文首先由12个反射界面模型合成地震记录,再以最大值的3%添加随机噪音。由此得到的单道含噪地震记录及其振幅谱分别如图1和2所示。

图2 原始地震记录的振幅谱Fig.2 The amplitude spectrum of the original seismic record
实验1 取白噪系数为0.001,固定相关时窗和反褶积因子长度分别为1 000和80 m s。由此得到常规脉冲反褶积后的地震记录与反褶积因子分别如图3和4所示,其振幅谱则分别如图5和6所示。通过对比可知:反褶积后的地震记录的振幅谱忽略其抖动后基本为全频带的,很明显频带得以拓宽,高频成分得到了提高,而在时域内则表现为地震记录的垂向分辨率有了明显提高,在反褶积前难以分辨的界面现已能够清晰分辨出来,但已出现了明显的高频噪音或者假频,使得有些界面反而淹没在其中。此外还可看出,此时的反褶积因子衰减变慢,其振幅谱包括反褶积后地震记录的振幅谱的高频段出现了较大的抖动现象。

图3 常规脉冲反褶积后的地震记录(白噪系数取为0.001)Fig.3 The seismic record after traditional spiking deconvolution with the w hite noise coefficient being 0.001
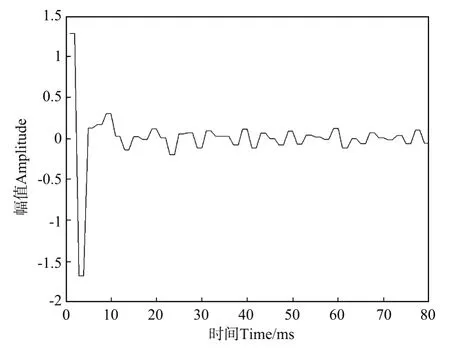
图4 白噪系数取为0.001时所计算的反褶积因子Fig.4 The computed deconvolution factor with the white noise coefficient being 0.001
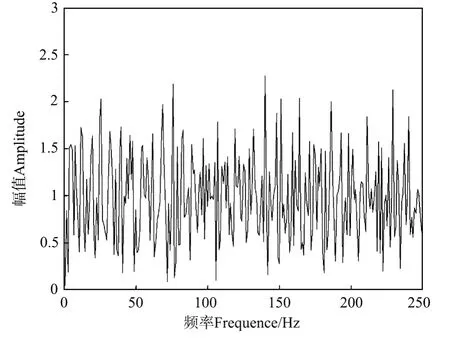
图5 反褶积后地震记录的振幅谱(白噪系数取为0.001)Fig.5 The amplitude spectrum of seismic record after deconvolution with the white noise coefficient being 0.001
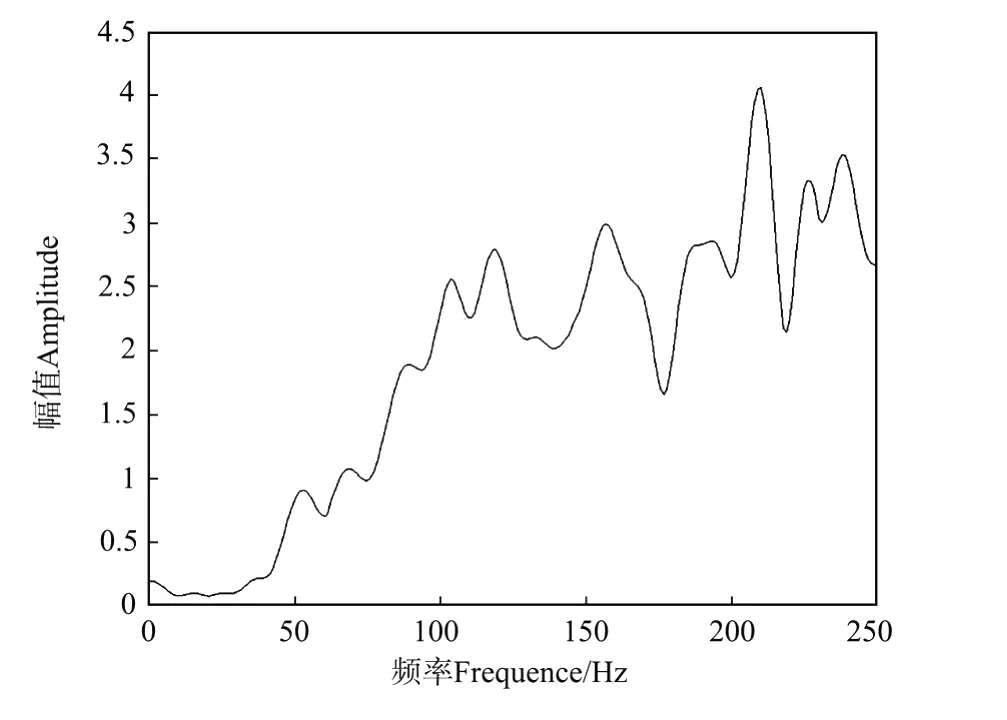
图6 白噪系数取为0.001时所计算的反褶积因子的振幅谱Fig.6 The computed amplitude spectrum of deconvolution factor with the white noise coefficient being 0.001
实验2 取白噪系数为0.5,同样固定相关时窗和反褶积因子长度分别为1 000和80 m s。由此得到常规脉冲反褶积后的地震记录与反褶积因子分别如图7和8所示,其振幅谱则分别如图9和10所示。通过对比可知:无论在时间域还是在频率域,此时的反褶积因子及其振幅谱的抖动程度明显变弱,在反褶积后的地震记录上则表现为分辨率与信噪比的进一步折衷。
在常规脉冲反褶积中,一般根据地震记录的信噪比确定白噪因子的数值。原始信号信噪比越高,白噪系数可取值越小,分辨率提升越高;原始信号信噪比越低,白噪系数取值须越大,分辨率提升越低。显然,白噪因子的值过小会造成高频噪音的过度抬升,信噪比相应过度下降,并非可靠地提高了分辨率,甚至出现假频;而其值过大又可能达不到压缩子波,提高地震分辨率的目的。因此,如何在信噪比与分辨率这一对矛盾中取得恰当的折衷是常规脉冲反褶积的一个难点问题。
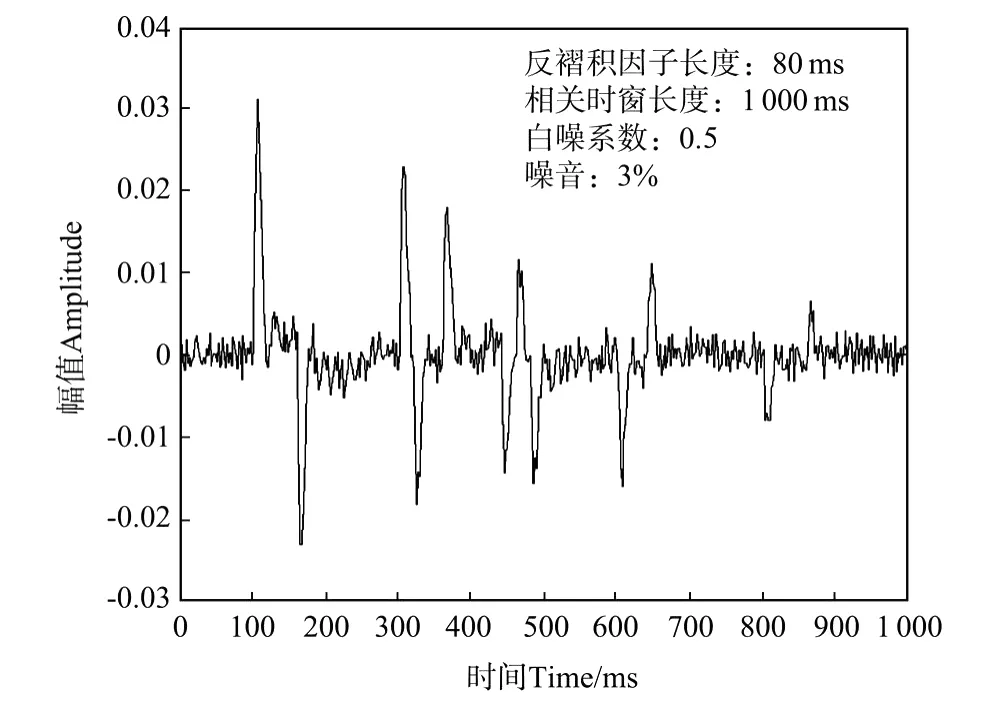
图7 常规脉冲反褶积后的地震记录(白噪系数取为0.5)Fig.7 The seismic record after traditional spiking deconvolution with the w hite noise coefficient being 0.5

图8 白噪系数取为0.5时所计算的反褶积因子Fig.8 The computed deconvolution factor with the white noise coefficient being 0.5

图9 反褶积后地震记录的振幅谱(白噪系数取为0.5)Fig.9 The amplitude spectrum of seismic record after deconvolution with the w hite noise coefficient being 0.5
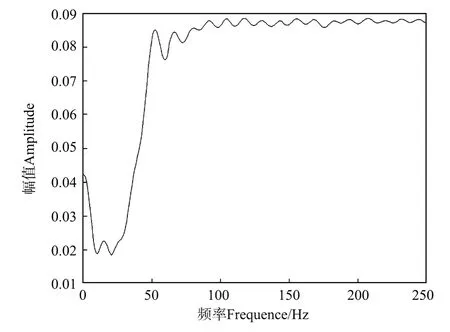
图10 白噪系数取为0.5时所计算的反褶积因子的振幅谱Fig.10 The computed amplitude spectrum of deconvolution factor with the white noise coefficient being 0.5
2 主能量脉冲反褶积
2.1 主能量脉冲反褶积的基本原理
如果地震记录中的噪音比较严重,常规的脉冲反褶积方法只能通过加大白噪系数的方式来折衷反褶积后地震记录的讯噪比和分辨率,难以达到理想的效果,且白噪系数大小没有1个直观的选取标准,只能通过实验效果来确定。
假设通过对地震记录的频谱分析和频率扫描确定出地震波的主频为fm,有效频带范围在f1~f2之间,此显然就是我们希望拓宽频谱的主要区间。现设计1个零相位的频谱M(f),使其在有效频带f1~f2之间接近于1(在主频fm处达到极大值1),而在f1和f2处迅速衰减为/2,且在有效频带范围之外衰减为非显著能量(如图11所示)。这样1个类型的频谱,即可作为我们希望输出的地震记录的振幅谱。为便于讨论起见,将M(f)称为主能量谱。

图11 主能量谱示意图Fig.11 The sketch map of main energy spectrum
事实上主能量谱M(f)又可视为1个将有效频带作为主要通频带的滤波器。让原始地震记录通过该滤波器后必然会提高其讯噪比。设原始地震记录为x(t),主能量谱M(f)对应的时间域信号为m(t),则经其滤波后的输出y(t)可表示为:
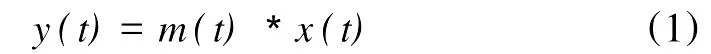
现将y(t)视为输入地震记录,按脉冲反褶积方法求取初步的反褶积因子b(t),则可得:

由于y(t)是1个经过主能量谱滤波后的地震记录,即使在原记录中高频噪音比较严重的情况下也能够明显提高讯噪比。一般来讲,当应用y(t)作为输入的地震记录时,即使选取1个很小的白噪系数β也能够通过(2)式获得1个稳定的初始反褶积因子b(t),此时如果令b(t)与y(t)进行褶积运算所得信号的振幅谱将是1个接近于常数的宽带谱。因此,可通过让主能量谱M(f)作为期望输出的振幅谱来进一步优化反褶积因子b(t),即令:

则c(t)即作为最终优化的反褶积因子。令其与y(t)进行褶积运算,即:
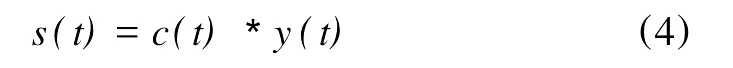
则s(t)即为经过主能量脉冲反褶积之后输出的地震记录。
简析:硫酸钠溶液存在H2O、Na+、和极少量的H+、OH-,通电时阳极上OH-(实质上可看作是H2O)被氧化导致H+浓度增大,阴极上H+(实质上也可看作是H2O)被氧化导致OH-浓度增大,同时H+向阴极定向移动,OH-向阳极定向移动,但电极反应的影响明显占主导。
2.2 时变主能量脉冲反褶积
由于大地介质的吸收衰减作用,随着记录时间的增大地震波的主频与有效频带的范围将越来越向低频方向移动,因此,在实际的地震记录中,不仅地震子波是时变的,而且地震波的主能量谱也是时变的。当整张地震记录/剖面中的主能量谱变化比较严重时,必须采用恰当的时变反褶积技术才能由浅到深均获得好的处理效果。
将地震记录分时窗处理是解决时变问题的1个基本思路。理论上讲,所划分的时窗个数应根据实际时变的程度来确定,时窗可以是等间隔的也可以是非等间隔的。实际处理时往往是按等间隔时窗将地震记录进行划分,在同一个时窗内可在假设地震子波和地震波的主能量谱是时不变的前提下求取反褶积因子。
假设将地震记录划分为N个时窗,所设计的主能量谱分别为Mi(f),i=1,2,…,N,其所对应的时域信号分别为mi(t),在各时窗内所求取的最终优化的反褶积因子分别为ci(t),由此即可在整张记录上插值出各点最终优化的反褶积因子c(t),再由式(4)即可计算反褶积之后输出的地震记录。
3 数值实验示例
图12为一模拟的含噪地震偏移剖面,其中:地震子波的主频在1 200 m s的记录长度范围内由起始的25 Hz降为20 Hz,剖面的起始和终止道的位置分别位于300和5 500 m处,其道间距为25 m,记录长度为1 200 m s,采样率为2 m s。原模型共有13层,速度变化范围为1 500~3 650 m/s,海底约位于85 m深度上(即在图12所示的时间剖面上约为113 m s处的同相轴),紧邻其下间隔约15 m存在第1个反射界面,其在时间剖面上与海底混合在一起,即在使加噪之前也难以分辨。
为了检验主能量脉冲反褶积对时变子波/主能量频谱的容时变能力,特仅用1个时窗进行反褶积处理。根据频谱分析(图13中较窄频带的曲线为原地震记录的振幅谱)和频率扫描(图示从略)可知:在1个时窗内,地震记录的主频约为19.5 Hz,有效波频带范围在5~60 Hz之间,据此设计的主能量频谱如图13中的较宽频带曲线所示,其再经过低截频(3~6 Hz)和高截频(60~200 Hz)带通滤波处理后即得期望输出的主能量频谱。

图12 模拟的含噪偏移剖面Fig.12 Themodeled migration section with noise

图13 所设计的主能量频谱(较宽频带曲线)与原地震记录的振幅谱(较窄频带曲线)Fig.13 The designed main energy spectrum(relatively wider curve)and the amplitude spectrum of the original seismic record(relatively narrow curve)

图14 主能量脉冲反褶积后的地震剖面Fig.14 The seismic section after Main Energy Spiking Deconvolution
理论上讲,即使在噪音比较严重的情况下,主能量脉冲反褶积仍可选用很小的白噪系数,这是其与常规脉冲反褶积的显著差别之一。为了验证这一结论,在实验中特取白噪系数为零值。图14给出了反褶积后的地震剖面,从中可以看出:在本例中,由主能量频谱所确定的期望输出结果可明显地压缩子波,已能较清晰地分辨出紧跟海底之下的第一个反射界面(图15示例了浅部区域纵向放大后的显示结果)。图16和17分别给出了反褶积前后地震剖面的振幅谱。比较可知:经反褶积后的频谱主要是在有效频带范围内拓宽,其与所设计的期望输出频谱(振幅谱)的形态基本吻合。

图15 对图14所示剖面浅部区域放大后的显示结果Fig.15 The scale-up section of the shallow part in Fig.14

图16 原始地震剖面(图12所示)的振幅谱Fig.16 The amp litude spectrum of the original section(as show n in Fig.12)

图17 反褶积后剖面(图14所示)的振幅谱Fig.17 The amp litude spectrum of the section after deconvolution(as show n in Fig.14)

图18 原始叠前时间偏移剖面Fig.18 The pre-stack timemigration section
4 实际地震资料处理示例
对实际地震资料进行主能量脉冲反褶积处理的思路与数值实验基本相同,其步骤可归结如下:
(1)对地震记录/剖面进行频谱分析,初步确定地震波的有效频带范围;
(2)根据频谱分析初步结果,给定频率扫描范围,并以一定的频率步长进行窄频带扫描分析;
(3)根据频率扫描分析结果,确定地震波的主频和有效频带范围;
(4)根据地震波的主频和有效频带宽度,设计主能量频谱;
(5)以主能量频谱为期望输出的振幅谱进行主能量脉冲反褶积处理,最终获得期望输出的地震记录/剖面。
图18和19分别给出了反褶积前、后的叠前偏移地震剖面示例(在处理中取白噪系数为0.000 1)。可见:主要在地震波的有效频带范围内拓宽频谱的主能量脉冲反褶积方法,不仅能可靠地提高地震记录的分辨率,同时还可避免高频噪音的提升,保持较好的信噪比。
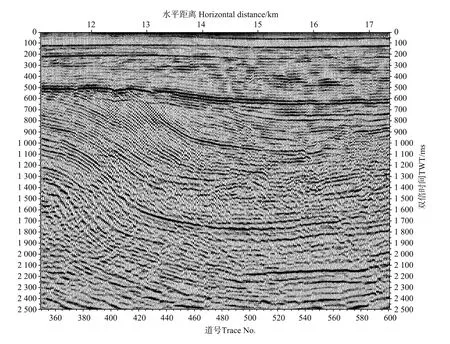
图19 主能量脉冲反褶积后的地震剖面Fig.19 The seismic section after Main Energy Spike Deconvolution
5 结论
(1)由于在频率域拓宽频带等同于在时间域压缩地震子波,因此主要在地震有效频带范围内拓宽频谱的主能量脉冲反褶积,可获得更为可靠的地震分辨率;
(2)与传统的脉冲反褶积相比,即使在原记录噪音比较严重的情况下,主能量脉冲反褶积方法仍可取很小的白噪系数而获得较好的反褶积效果;
(3)通过设计合理的期望主能量谱,主能量脉冲反褶积方法不仅能可靠地提高地震资料的分辨率,同时还可避免高频噪音的提升,保持较好的信噪比;
(4)通过主能量脉冲反褶积获得较好处理效果的关键是精确地确定地震波的有效频带范围,对此本文提出了通过频谱分析和频率扫描的技术手段来确定的模式。如何结合其它的方法技术更加精确地确定地震波的有效频带范围,进而更为合理地设计期望输出的主能量谱,将是今后的研究问题之一。
[1] 熊翥.复杂地区地震数据处理思路[M].北京:石油工业出版社,2002.
[2] Robinson E A.Predictive decomposition of seismic traces[J].Geophysics,1957,22(4):767-778.
[3] Burg J P.Maximum Entropy Spectral Analysis[C].[s.l.]:Proc.of the 37th Meeting of the Society of Exploration Geophysicists,1967
[4] Peacock K L,Treitel Sven.Predictive deconvolution:theory and p ractice[J].Geophysics,1969,34(2):155~169
[5] Robinson J C.Computer-designed wiener filters for seismic data[J].Geophysics,1972,37(2):235-259.
[6] Wiggins R.Entropy guided deconvolution[J].Geophysics,1985,50(12):2720-2726.
[7] 余日可,岳继光.子波最小相位对最小平方反褶积效果影响[J].电子测量技术,2008,31(2):15-19.
[8] 徐伯勋,白旭滨,于常青.信号处理及应用[M].北京:地质出版社,1997,35-124.
The Main Energy Spiking Deconvolution
LIJin-Shan1,2,JIANG Xiu-Ping1,2,WANG Xiu-Tian1,2
(1.College of Marine Geosciences;2.The Key Lab of Seafloor Science&Exp lo ration Technique,Ministry of Education,O-cean University of China,Qingdao 266100,China)
The main energy spiking deconvolution app roach is presented in this thesis.The method can maintain the frequency phase characteristics of the original deconvolution and expand the frequency bandwidth within the effective range to a desired so-called main energy spectrum.This is expected to achieve a more reliable seismic resolution.Themain energy spiking deconvolution processing can be divided into the following steps.Firstly,the effective seismic bandwidth is determined by using the frequency spectrum analyzing and scanning,and a main energy spectrum is designed to be expected as the output based upon the analyzing result.Secondly,a main energy signal is obtained by using the main energy spectrum filtering,and an initial deconvolution operator is computed by taking themain energy signal as the input.It is then to calculate the op timum deconvolution operator series based upon the rule that the frequency phase characteristics of the initial deconvolution operator is maintained and the main energy spectrum is to be taken as a desired amplitude spectrum.Finally,the desired seismic signal is outputted by the simple convolution operation.
deconvolution;seismic effective bandwidth;main energy spectrum;white noise coefficient
P631.4+14
A
1672-5174(2011)7/8-119-08
国家科技重大专项(2008ZX05025-001-006)资助
2010-12-10;
2011-05-09
李金山(1963-),男,高级工程师。E-mail:ljs@ouc.edu.cn
**通讯作者:E-mail:xtwang@ouc.edu.cn
责任编辑 徐 环

