幂群的等价条件及其性质的研究

张朝凤,王连平

(1.吉林大学数学中心,吉林长春 130012; 2.吉林大学计算机中心,吉林长春 130012)

幂群的等价条件及其性质的研究

张朝凤1,王连平2

(1.吉林大学数学中心,吉林长春 130012; 2.吉林大学计算机中心,吉林长春 130012)

在幂群概念及已有性质的基础上,给出了循环群幂群、一般幂群的等价条件,并给予了严格的证明.提出了幂群的一些新的性质,得到了一些有意义的结论.

幂群;循环幂群;等价关系

1 预备知识

本文始终假定(G,·)是一个群.在P(G)-{Φ}中规定代数运算[1]:

取非空集类g⊂P(G)-{Φ},如果g关于运算(1.1)做成群,则称g为G上的一个幂群.其单位元用E表示.

特别称g是G上的一个正则幂群,如果e∈E,这里e是G的单位元.

定理1.1[2-4](基数定理)设g是群G上的幂群,则对任意一个A∈g,有|A|=|E|.若g是群G的幂群,置是半群.

设E是G的含单子半群,称E是G的正规子半群,如果E满足条件:对任意x∈G,有x E=Ex.

定义1.1[5]设E是G的正规子半群,则{x E|x∈G}是G的幂群,称为G的广义商群.

2 循环群的幂群的等价条件

设G=〈a〉是循环群,A={aj1,aj2,…,ajn,…}∈G,且A中列出的元素两两互异,则称Ap={j1, j2,…,jn,…}为A的指数集,称A为A p相应的元素集.

取g⊂P(G)-{Φ},记gp={Ap|A∈g}.

设m为正整数,X为一整数集,且对任意a,b∈X,a≠b(modm),则称X为关于m的非同余数集.

设m为正整数,X,Y都是关于m的非同余数集.如果对每个a∈X,有b∈Y,使a≡b(modm),且对每个d∈Y,有c∈X,使d≡c(modm),则称X与Y是关于m的等价组.记为X≡Y(modm).

注2.1如果X与Y是关于m的等价组,则有|X|=|Y|.

注2.2如果X与Y是关于m的等价组,则称X与Y关于m有关系“～”,显然“～”是整数集间的等价关系.

设G=〈a〉是循环群[6-8],g⊂P(G),g≠Ø,定义g的指数幂集的子集gp中的加法[3]:

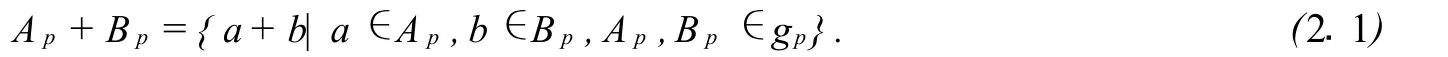
命题2.1设G=〈a〉为有限循环群,且o(G)=m,g是G上幂集的子集,则g是幂群的充要条件是gp满足如下条件:

(1)对任意Ap,Bp∈gp,存在Cp∈gp,使Ap+Bp≡Cp(modm);

(2)存在Ep∈gp,使得对任意Ap∈gp,有Ap+Ep≡Ap(modm);

(3)对任意Ap∈gp,存在Bp∈gp,使Ap+Bp≡Ep(modm).

证明必要性:如果g是G上幂群,则对任意Ap,Bp∈gp,考虑相应的元素集A,B,则有C∈g,使C=AB,于是有Cp∈gp,使Cp≡Ap+Bp(modm).

事实上,∀s∈Cp,有as∈C且as=ak·al,其中ak∈A,al∈B,即s≡k+l(modm);反过来,对任意k′+l′∈Ap+Bp,有ak′+l′∈AB=C,故有as′∈C,使ak′+l′=as′,从而k′+l′≡s′(modm),条件(1)得证.

与上面的讨论类似,可由群的单位元的存在性,推知条件(2)被满足;可由群的逆元的存在性推知条件(3)被满足.

充分性:如果g的指数幂集的子集gp满足条件(1)—(3),则:

(ⅰ)对任意A,B∈g考虑A和B的指数集Ap和Bp.由条件(1),存在Cp∈gp,使Ap+Bp≡Cp(modm).这样,∀ai∈A,aj∈B,存在k∈Cp,使i+j≡k(modm),相应的有ai+j=ai·aj=ak∈C;而∀ak′∈C,应有i′∈Ap,j′∈Bp,使i′+j′≡k′(modm),即有ai′∈A,aj′∈B,使ak′=ai′+j′=ai′·aj′,即得到C∈g,使AB=C∈g,g对乘法封闭.

(ⅱ)由条件(2)中Ep的存在性,同条件(ⅰ)的讨论类似,可证明g中与Ep相对应的元素E∈g即为g的右单位元.

(ⅲ)∀A∈g,由条件(3),考虑A的指数集A p,知有Bp∈gp,使Ap+Bp≡Ep(modm),则同(ⅰ)的讨论类似,可知与Bp相对应的B∈g即为A在g中的右逆元.

综合(ⅰ)—(ⅲ)可得g为G上幂群.

注2.3显然(2.1)式中定义的加法可交换,并由此可知命题2.1的条件(1)—(3)中做和的两项可交换.

命题2.2有限循环G的阶为m,那么G上的幂群(g,·)与(gp,+)同态,因而(gp,+)为整数加群中的幂群.

则由gp的定义即知φ是g到gp的满射.

又对A,B∈g,由基数定理可设

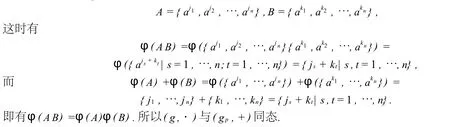
推论2.1有限循环群幂集的子集g关于运算(1.1)所给的乘法做成幂群的充要条件是g的指数集的子集gp关于整数集类的等价系(可视为相等关系),在运算(2.1)所给的加法下做成(整数集类的)幂群.

与命题2.2的讨论类似,我们立刻可得下面的命题.

命题2.3设G=〈a〉为无限循环群,g⊂p(G)-{Ø},则g关于运算(1.1)给出的乘法做成幂群的充要条件是gp满足:

(1)对任意Ap,Bp∈gp,存在Cp∈gp,使Ap+Bp=Cp;

(2)存在Ep∈gp,使对任意Ap∈gp,有Ap+Ep=Ap;

(3)对每个Ap∈gp,都存在Bp∈gp,使Ap+Bp=Ep.

命题2.4设G为无限循环群,G上的幂群(g,·)与g指数幂集的子集gp关于运算(2.1)中加法做成的有运算集(gp,+)同构.

推论2.2无限循环群幂集的子集g,关于运算(1.1)所给的乘法做成幂群的充要条件是g的指数幂集gp关于运算(2.1)所给的加法做成幂群.

3 一般幂群的等价条件

定义3.1设G是群,g⊂p(G)-{Ø},对于A,B∈g,如果存在C∈g,使AC=B,则称A在g中可经C右传递到B,简称A(在g中)可右传到B.记为A～CB.如果存在D∈g,DA=B,则称A在g中可经D左传递到B,简称A可左传到B.记为AD～B.如果A既可左传到B,亦可右传到B,则A可传到B,记为A～B.

如果∀A,B,C∈g,A～B D,AC～K时总有D,K∈g,则称g为关于运算(1.1)中乘法的传递闭包,简称g为一个传递闭包.

命题3.1设G是群,g⊂p(G)-{Ø},则g是关于运算(1.1)中乘法的传递闭包的充要条件是∀A,B,C∈g,都有AB,CA∈g.

命题3.2 设G是群,g0⊂p(G)-{Ø},令

命题3.5设G是群,g⊂p(G)-{Ø},g是G上一个幂群,当且仅当以下条件满足:

(1)g是关于运算(1.1)中乘法的传递闭包;

(2)∀A∈g,A都可经g中同一元E右传递到A;

(3)对每个A∈g,A都可右传递到E.

证明(ⅰ)如果g是G上幂群,则∀A,B和C∈g,由命题3.1知AB和CA∈g,从而g为一个传递闭包.

(ⅱ)g中存在单位元E,使∀A∈g,有A E=A,即A～E A,也即g中任一元A都可经g中同元右传到本身.

(ⅲ)对每个A∈g,存在A-1∈g,使AA-1=E,即A～A-1E,亦即A总可右传递到E.反之,如果g⊂p(G)-{Ø},且满足条件(1)—(3),则:

(ⅰ)对A,B∈g,由命题3.1,总有AB∈g,故g对乘法封闭;

(ⅱ)因g中每一元都可经同元E右传递到本身,即对A∈g,有A～EA,A E=A成立.故E为g中右单位元;

(ⅲ)因对每一A∈g,有B∈g,使A～B E,即AB=E,所以每一元A∈g都有右逆元,即g为关于运算(1.1)乘法的幂群.

注3.1显然,将命题3.5中条件(2)和(3)里的“右”全改为“左”,命题3.5的结论不变.若将条件(2)和(3)里的“右”全删去,命题的结论亦成立.

定义3.2设G是群,g⊂p(G)-{Ø},称

为A在g中关于Ei的右可除元集.

如果对一切A∈g,β(A,Ei)≠Ø,那么称Ei为g的一个右单位元;称β(A,EI)中元A为q的右逆元.由群论知识可知,g的右单位元即g的左单位元,也即g的单位元,且唯一.又g的一个元的右逆元,即它的左逆元,也即它的逆元,且唯一.

命题3.6设G是群,g⊂p(G)-{Ø}是G上的幂群,当且仅当以下条件被满足:

(1)g是关于运算(1.1)中乘法的传递闭包;

反之,如果G上g⊂p(G)-{Ø},且g满足条件(1)—(3),则显然g对运算(1.1)的乘法封闭.

又因为存在Ei∈ε,使每个A(A∈g)的右可除元集β(A,Ei)≠Ø,故Ei即是g对运算(1.1)中乘法的单位元.事实上,对每个A∈g,因Ei∈εA,有A Ei=A.

再由β(A,Ei)≠Ø,知存在B∈g,使AB=Ei,这就证得g为G上的幂群.

(2)g的右单位元胚集ε≠Ø;

(3)对g存在Ei∈ε,使得每个g中元A的右可除元集β(A,Ei)≠Ø.

证明如果g是G上的幂群,则条件(1)显然被满足.又由g中存在单位元E,故对每一个A∈g,有

4 其他性质

命题4.2设G为一个群,g是G的幂群,E是g的单位元.如果e∈A⊂g,则总有A-1⊂E⊂A.

由命题4.1的证明,知E⊂A.且E=AA-1=[E∪(A|E)]A-1=A-1∪(A|E)A-1,即得A-1⊂E.

[1] 李洪兴,汪培庄.幂群[J].应用数学,1988(Z1):1-4.

[2] L IHONG XING.HX group[J].BUSEFAL,1987,33:31-37.

[3] L IHONG XING.HX group[J].BUSEFAL,1988,34:14-17.

[4] 李洪兴.正则HX群的同态与同构[J].模糊系统与数学,1990,4(1):1-7.

[5] 何清,李洪兴.幂群的表示与同构的提升[J].北京师范大学学报:自然科学版,1999,35(1):32-37.

[6] 张禾瑞.近世代数基础[M].北京:高等教育出版社,1998:60-101.

[7] M·赫尔.群论[M].裘光明.北京:科学出版社,1981:40-87.

[8] 刘晓蕾,王燕鸣.有限群的p-幂零性的一个注记[J].吉林大学学报:理学版,2009,47(3):523-526.

The equal value requirement and nature of power group

ZHANG Chao-feng1,WANG Lian-ping

(1.Centre of Mathematics,Jilin Univesity,Changchun 130012,China; 2.Centre of Computer,Jilin Univesity,Changchun 130012,China)

On the basis of the pow er group concep t and the exited nature,this thesis w ill further put forw ard some equal value requirement for the power group of cycle group and the general power group.Furthermore,this thesis has p roved strictly and puts forward some other natures of power group.Therefore,some meaningful conclusions have been obtained.

power group;power group of cycle;equivalence relation

O 152

110·2115

A

1000-1832(2010)04-0026-04

2010-08-20

国家自然科学基金资助项目(10871057).

张朝凤(1962—),女,副教授,主要从事代数理论研究.

(责任编辑:陶 理)