一种基于知识编译的模型计数方法

殷明浩,刘 华,谷文祥

(东北师范大学计算机科学与信息技术学院,吉林长春 130117)

一种基于知识编译的模型计数方法

殷明浩,刘 华,谷文祥

(东北师范大学计算机科学与信息技术学院,吉林长春 130117)

提出一种新的基于知识编译的模型计数方法——M TREE.该方法以一个否定范式(NF)作为输入,利用命题表推演过程,结合香农扩展和简化规则,将输入的否定范式编译成与之等价的R-模型树,在R-模型树上应用多项式时间算法求出其模型个数,即为原输入NF的模型个数.严格证明了该算法是完备有效的.

模型计数;知识编译;否定范式;模型树;R-模型树;香农扩展

0 引言

模型计数(#SA T)是求解给定命题公式模型个数的问题,是命题可满足问题(SA T)的泛化,其计算复杂性高于SA T,是标准的#P完备问题.随着SA T研究的日益成熟,许多NP问题都可以转化成SA T求解,如智能规划问题.有些求解难度高于NP的问题无法转化成SA T求解,却可以转换成#SA T求解,如一致性规划问题和概率推理问题[1-2].模型计数正日趋完善,目前模型计数可分为精确模型计数和近似模型计数,精确模型计数已经可以求解数百变量规模的问题,而近似模型计数已经可以求解上千变量规模的问题.其中精确模型计数是源于SA T求解方法的,它可以分为两类:一类是基于DPLL的,扩展系统DPLL式SA T求解器求解模型计数问题最早是由E.Birnbaum和E.L.Lozinskii在其模型计数器CDP中提出的[3];另一类是基于知识编译的,简单来说这种方法是将要求解的命题公式先编译成与之逻辑等价的一种易处理的目标语言,再用一个多项式时间算法计算该目标语言的模型个数.现有的基于知识编译的模型计数有文献[4]中提到的Darw iche的编译器c2d和文献[5]中提到的基于扩展规则的模型计数器JLU-ERWMC,其中文献[4]将CNF编译成d-DNNF来求解模型个数;文献[5]则是以CNF作为输入,利用扩展规则求解模型个数.文献[4-5]中算法均依赖于CNF,不是所有的命题公式都能在多项式时间转换成CNF,所以已有的这两种算法不能对所有命题公式的模型个数求解.本文在基于知识编译的基础上提出一种新的模型计数方法——基于表推演的模型计数算法M TREE,该方法能求解所有命题公式的模型个数.M TREE以否定范式(NF)作为输入,先将原公式编译成一棵与之等价的R-模型树,之后在多项式时间内遍历R-模型树求出原公式模型个数.M TREE方法是完备有效的,并且编译后模型计数是多项式时间的.

1 相关概念

为便于展开讨论,对本文中使用的符号进行如下约定:Σ,α,β…表示命题公式;Ai,F,G表示子命题公式;p,pi表示变量,其中i={1,2,…},pi,pi,…表示变量对应的文字;VAR(Σ)表示一个命题公式Σ中所有变量的集合;T表示一个表推演(tableau).

表推演方法是一种经典逻辑和各种非经典逻辑统一的推理框架.以下表推演相关定义见文献[6].

定义1.1(表推演tableau)令{A1,A2,…,An}为公式的有限集合.

(1)下列分枝树为公式{A1,A2,…,An}的一个表推演:

(2)如果T为{A1,A2,…,An}的一个表推演,且T′为T应用表推演扩展规则后的结果,那么T′也是{A1,A2,…,An}的一个表推演.

利用表推演进行定理证明可以将命题公式分为两类:α型公式和β型公式.见图1-2.

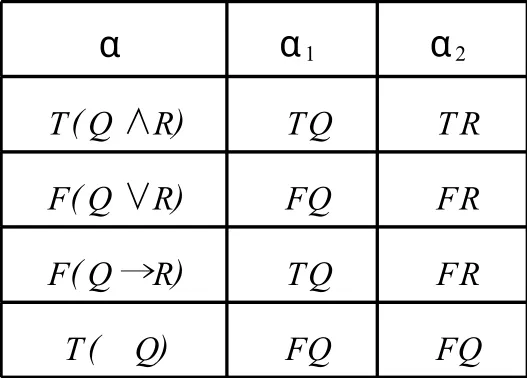
图1 α型公式

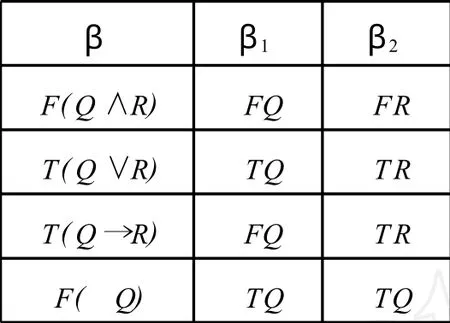
图2 β型公式

根据α型公式和β型公式可得到命题表推演的扩展规则:

定义1.2(命题表推演扩展规则)

α扩展规则处理α型公式,若使命题公式α成立必须使命题公式集{α1…αn}同时成立;β扩展规则处理β型公式,若使命题公式β成立,命题公式集{β1…βn}中一个成立即可.

本文采用树形结构表示α和β扩展规则,同一分支上节点为合取关系(α扩展规则),分支之间为析取关系(β扩展规则).形式如图3.

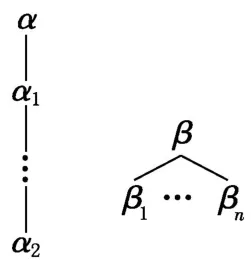
图3 树形结构

本文提出的基于知识编译模型计数方法——M TREE,是将表推演过程结合香农扩展规则和简化规则实现的.其定义见文献[7].

定义1.3(香农扩展)给定任意的一个命题公式Σ和一个变量p,Σ关于p的香农扩展:

文献[8]中已经证明经过香农扩展的命题公式与原公式是逻辑等价的.

给定任意的命题公式Σ,假设F,G是Σ的任意子公式,令Σ[G/F]表示用G替换Σ中所有子公式F的结果.p是Σ中的一个变量.本文将用到如下简化规则:

定义1.4[9](否定范式NF)由变量、逻辑常量0,1及二元连接符∧,∨,⇔构成命题公式.

定理1.1[7]所有的命题公式都可以在线性时间内转换成NF.

2 模型树

本文提出的M TREE方法是将输入的否定范式转换成与之等价的R-模型树来处理的,模型树、R-模型树定义如下:

定义2.1(模型树)令VAR(Σ)={p1,…,pn}为任意命题公式Σ的变量,Σ的模型树是以1为根, p1和p1分别为其左右子树的根,pi+1和pi+1分别为pi和pi的左右子女,pn和pn为叶子节点,同一分支上所有文字取正后Σ为真的分支组成的与或二叉树.

注模型树为n+1层,规定根为第0层,第i层节点由变量pi的文字标记,每个分支上不会出现相同变量,并且树的同一分支路径上的节点是与(∧)关系,分支间节点是或(∨)关系,一个分支路径上所有文字为真即是Σ的一个模型.不可满足的命题公式的模型树为空树.

例2.1令Σ=p1∧(p2⇔p3),它的模型树如图4.

图4 Σ的模型树

图5 R-模型树

定理2.1命题公式的模型树与其本身是逻辑等价的.

证明根据定义2.1,我们知道模型树遍历命题公式中所有变量取值情况,是类DPLL的,讨论所有赋值情况之后保留所有使命题公式为真的分支,这样得到的模型树与原命题公式解相同,即为逻辑等价的.

定理2.2求解一棵模型树的模型个数可以在多项式时间完成.

证明求解一棵模型树的模型个数只需遍历该模型树,记录数的分支个数d,model_c=d.显然算法是树宽的线性时间.

根据定义2.1,要用模型树表示一个有效的命题公式,则需要一个n+1层的完全二叉树,这种表示非常浪费空间,因而我们给出简化模型树(R-模型树).

R-模型树是在模型树的基础上应用简化规则SR5-SR8得到的,简化后R-模型树与模型树是逻辑等价的.规则中合取关系是在同一路径上,析取关系在两个分支之间.这样得到的R-模型树叶子节点不存在叶子兄弟,树的层数至多为n+1层,有效命题公式的R-模型树将只有根节点1.

例2.2将例2.1中模型树转换成R-模型树.

显然,当模型树中存在多对兄弟叶节点时,简化可以有效地节约空间.这里的M TREE算法采用R-模型树,如图5.

定理2.3求解一棵R-模型树的模型个数可以在多项式时间完成.

证明一个命题公式对应的R-模型树有三种形式:

(1)R-模型树为空,表示该命题公式无解.

(2)R-模型树只含根节点1,表示命题公式是有效的,即有2n个解.

(3)R-模型树含有文字节点,其分支有两种:一种是含n个变量文字,这样的分支是命题公式的一个解;另一种变量文字个数为c(c＜n),没在分支中出现的变量取值0或1均可,这样的分支包含命题公式2n-c个解.我们用d表示R-模型树中的分支数,ci记录第i个分支的文字个数,命题公式的模型个数

综上所述,计算一棵R-模型树的模型个数是树宽的线性时间.

3 模型计数方法——M TREE

将输入的NF公式Σ编译成与之等价的R-模型树,再利用多项式时间算法求出模型个数.编译过程是用表推演结合香农扩展和简化规则完成的.具体算法如下:

定理3.1M TREE算法是完备有效的.

证明(完备性)M TREE方法以NF作为输入,根据定理1.1,它可以处理所有命题公式的模型计数问题.

(有效性)M TREE方法中的表推演过程、香农扩展、简化规则都保证公式的等价性,所以算法是有效的.

例3.1 求p1∧(p2⇔p3)的模型个数.

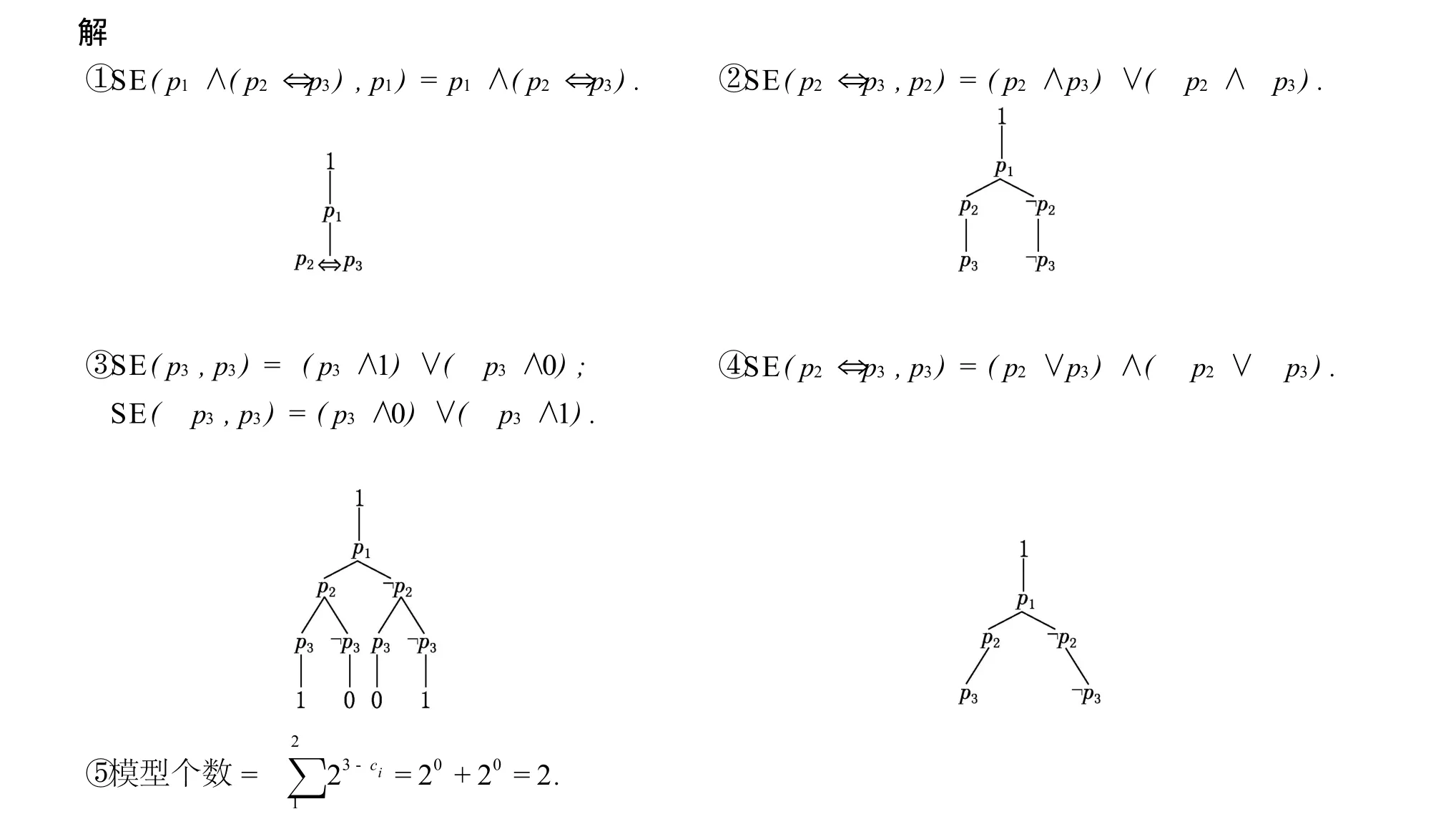
算法说明:首先设置R-模型树的根节点为1,从下标为1的变量开始,每个分支都会对应一个Σ(每个分支上的Σ不同),对Σ先简化再香农扩展,简化可以减少香农扩展的难度或直接剪枝(Σ=0删除该分支,Σ=1停止扩展该分支),香农扩展是为表推演过程按顺序扩展出变量,之后利用β规则和α规则推演,如此循环直到i=n.该算法与文献[4-5]中的方法比较其优点在于:它具有完备性,不依赖任何一种命题语言,能求解所有命题公式的模型计数问题.

4 总结

提出一种新的知识编译模型计数方法——M TREE.对本算法我们提出了R-模型树,它能完备有效地表示一个NF公式,并可以在多项式时间内求出其模型个数.M TREE算法通过表推演结合香农扩展和简化规则,将输入的NF命题公式编译成文中给出的R-模型树,再利用一个多项式时间算法求出输入公式的命题个数.理论证明M TREE方法不依赖任何一种命题语言,是完备有效的.

[1] HÉCTOR PALACIOS,BLA IBONET,ADNAN DARW ICHE,et al.Pruning conformant plans by countingmodelson compiled d-DNNF rep resentations[C]∥Monterey,California:Proceedings of ICAPS,AAA IPress,2005:141-150.

[2] STEPHEN M MAJERCIK,M ICHAEL L.Littman:contingent planning under uncertainty via stochastic satisfiability[J]. A rtificial Intelligence,2003,147(1/2):119-162.

[3] BIRNBAUM E,LOZINSKII E L.The good old Davis-Putnam p rocedure helps counting models[J].Journal of A rtificial Intelligence Research,1999,10:457-477.

[4] DARW ICHE A.New advances in compiling CNF into decomposable negation normal form[C]∥In Proceedings of ECA I-04: 16th European Conference on A rtificial Intelligence,Spain:Valencia,2004:328-332.

[5] 殷明浩,林海,孙吉贵.JLU-ERWMC:基于扩展规则的#SA T求解系统[J].软件学报,2009,20(7):1714-1725.

[6] 刘全,孙吉贵,于万钧.基于tableau的自动推理技术综述[J].计算机科学,2005,32(11):1-5.

[7] REINER HÄHNLE,NEIL V MURRA Y,ERIK ROSENTHAL.Normal forms for know ledge compilation[C]∥New York: ISM IS,2005:304-313.

[8] SHANNON C E.A symbolic analysis of relay and sw itching circuits[J].Transactions of the A IEE,1938,57:713-723.

[9] DARW ICHE A,MARQUISP.A know ledge compilationmap[J].Journalof A rtificial Intelligence Research,2002,17:229-264.

A model coun ting method using knowledge com pilation

YIN M ing-hao,L IU Hua,GU Wen-xiang

(College of Computer Science and Information Technology,Northeast Normal University,Changchun 130117,China)

A model counting methods using know ledge compilation w as p roposed,it w as called M TREE.This method used a negated form as input,and used p ropositional tableau,together w ith Shannon expansion and simp le rules made the input compiled into a R-model tree w hich w as logical equal to the input NF,then used a polynomial algorithm to compute themodel number of the R-model tree,also the input NF's.Thismethod w as p roved comp lete and valid.

model counting;know ledge compilation;normal form s;model tree;R-model tree;Shannon expansion

TP301

520·10

A

1000-1832(2010)04-0046-05

2009-06-04

国家自然科学基金资助项目(60473042,60573067,608003102).

殷明浩(1979—),男,博士,讲师,主要从事自动推理与智能规划研究;谷文祥(1947—),男,教授,博士研究生导师,主要从事计算机网络管理与智能规划、规划识别研究.

(责任编辑:陶 理)