风电场风速时间序列的复杂动力学特性分析

王东风,张有玥,韩 璞,徐大平

(华北电力大学自动化系, 河北 保定071003)

风力发电是当今世界增长最快的可再生能源,许多国家把发展风电作为改善能源结构、减少环境污染和保护生态环境的一种措施纳入国家发展规划[1] .目前, 国内外对风力发电相关问题的研究越来越深入和广泛, 但关于风电场风速预测的研究还不能达到令人满意的程度[2].主要原因是风速受温度、气压、地形、海拔等多种因素影响, 具有很强的随机性,要得到较精确的预测结果,难度很大.事实上,风速不完全是一种随机信号, 在很大程度上包含有确定性的一面, 至少在短时间内具有可预测性.因此,如果能证明风速是某个确定性混沌系统产生的, 就有助于掌握它的演变规律, 引入混沌方法对风速进行预测.这对提高预测精度将起着非常重要的作用.

本文的主要目的就是检验风速是否具有混沌特征.为避免理论假设对分析结果的影响,采用我国某大型风电场的实测数据分析.据混沌学理论, 可从以下几个方面来判断一个过程是否根源于某个混沌系统[3] :①过程是有界的;②过程是非线性的;③随着嵌入维数增加, 关联维数有限;④对初始条件的敏感性,即至少有1 个Lyapunov 指数为正;⑤所有Lyapunov 指数之和为负.如果其中任何一条不成立,则可肯定该信号不是由混沌系统产生的.对风速时间序列来说,如果条件③, ④成立, 则①, ②, ⑤就易验证.因此, 在介绍关联维数和Lyapunov 指数的有关概念和计算方法后, 主要对条件③, ④验证.结果表明,风速时间序列确实具有混沌系统的这些典型特征.

1 风速时间序列的混沌特性分析

1 .1 由时间序列重构动力学相空间

据Takens 嵌入定理[4],对一个时间序列, 只要嵌入维数足够大,即延迟坐标的维数M≥2D+1(D是动力系统的维数),在该嵌入维空间里可将有规律的轨道(吸引子)恢复出来,即重构空间中的轨道与原动力系统保持微分同胚, 与原吸引子的拓扑结构完全相同.对混沌时间序列x1 ,x2,…,xn-1 ,xn,若嵌入维数为m,延迟时间为τ, 则相空间重构为

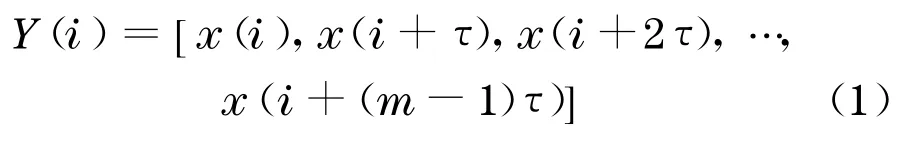
其中,i=1 ,2,…,N,N=n-(m-1)τ.式(1)中任一相点都包含有m个分量(或状态点),对N个相点在m维的相空间中构成一个相型, 相点间的连线是描述系统在m维相空间中的演化轨迹, 重构后的样本数为N.在重构相空间的过程中, 时间迟延和嵌入维数的选取具有十分重要的意义, 二者的恰当选取直接影响到相空间重构的质量,进而影响到预测精度.嵌入维数太低, 会出现吸引子的自交性;太高, 则使点与点之间的距离太远.时间延迟太小,重构吸引子相邻点的相关性太强, 吸引子的分析很容易被噪声干扰;时间延迟太大, 本来较近的向量也会拉远, 而导致不确定的系统状态[5].

1.2 最佳嵌入维数m 与延迟时间τ的确定

近些年的研究表明, 影响相空间重构质量的主要因素,不只在于单独选取延迟时间τ和嵌入维数m,更重要的是将τ和m联合起来的嵌入窗宽τw=(m-1)τ的确定.C-C 法[6]通过序列的关联积分来构成统计量, 统计量代表了非线性时间序列的相关性.通过统计量和延迟时间的关系图同时计算出τ和τw,从而确定出嵌入维数.定义统计量

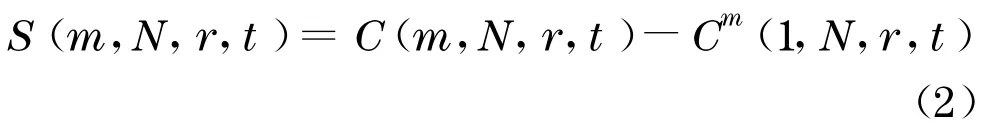
式中:C是嵌入时间序列的关联积分[6].

把时间序列{x(ti),i=1,2,…,N}分成t个不相交的时间序列,t=1 时为单个时间序列本身,t=2 时为{x(t1),x(t3), …,x(tN-1)}和{x(t2),x(t4), …,x(tN)},长度为N/2 .对t个不相交子序列,有

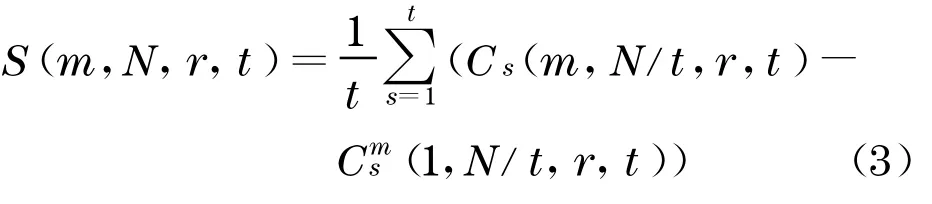
若序列独立同分布, 对固定的m和t,当N→∞,对所有的r,均有S(m,r,t)恒等于零.但实际序列是有限的,故一般S(m,r,t)不等于零.定义

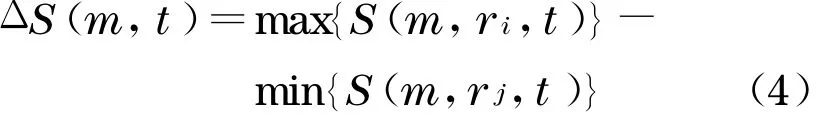
为关于r的最大偏差.一般地,N,m,r的选择有一定范围.当2 ≤m≤5,σ/2 ≤r≤2σ(σ指时间序列的均方差或标准差),N≥500 时,渐进分布可以通过有限序列很好地近似.具体计算时, 可以取m=2 ,3 ,4 ,5 ,r i=iσ/2 ,i=2 ,3 ,4 ,5 .计算下列3 个统计量:

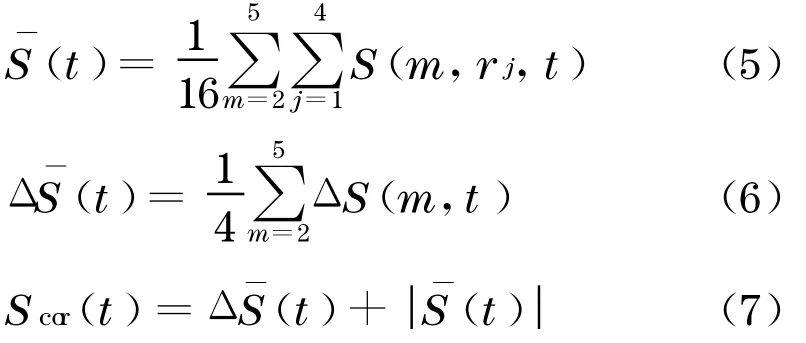
最佳迟延时间对应(t)第1 个零点,或Δ(t)的第一极小值,Scor(t)最小值对应的时间为最佳嵌入窗宽τw .C-C 方法计算量小, 对小数据组可靠, 实际应用表明该方法还具有较好的抗噪声能力.

1 .3 吸引子关联维数的计算

G-P 算法[7]是最常用的确定关联维数的方法.步骤如下:首先,在获得τ后,利用时间序列{x(ti),i=1 ,2,…,N},先给定一个较小的嵌入维数m0,则对应一个重构相空间Y(t i)=[x(ti),x(ti+τ),x(t i+2τ), …,x(ti+(m0-1)τ)] ;计算关联函数

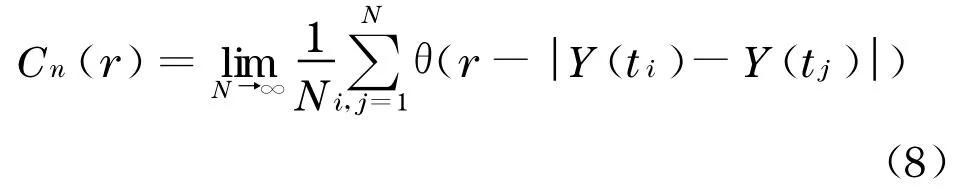
1 .4 风速时间序列最大Lyapunov 指数的提取

通常对最大Lyapunov 指数的估计有小数据量法[8] 和Wolf 法[9].为了减少计算量和人为因素影响,提高计算最大Lyapunov 指数的效率和精度, 采用文献[10] 给出的小数据量改进算法.首先对风速时间序列{x(ti),i=1,2,…,N}进行快速傅里叶变换(fast fourier transform ,FFT),计算平均周期P;由C-C 方法确定延迟时间τ和嵌入维数m并重构相空间{Y j,j=1,2,…,M};寻找相空间中每个点Y j的最近邻点Y j^,并限制短暂分离,即

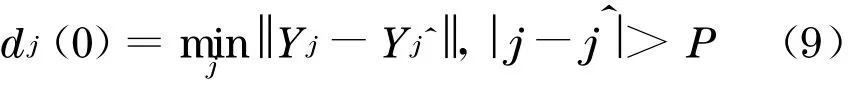
然后,对相空间中每个点Y j,计算出该邻点所对应的i步离散时间后的距离d j(i):

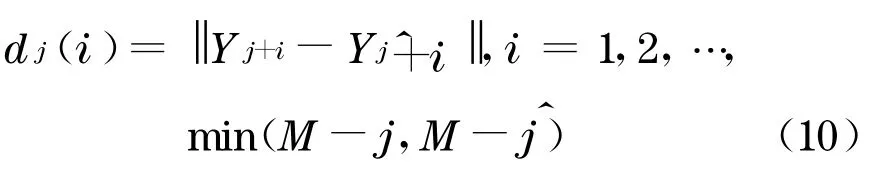
最后, 对每个i,求出所有j的lnd j(i)平均值y(i),即

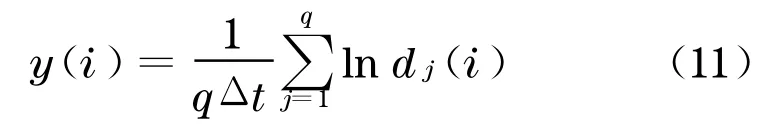
其中,q为非零d j(i)的数目.用最小二乘法作出回归直线, 该直线的斜率就是最大Lyapunov 指数λ1.该方法充分利用了序列的演变信息,对小数据组可靠,而且计算精度较高, 操作相对容易.

2 风电场风速序列实例分析

2.1 实例分析一

以我国某大型风电场的实测风速为例, 采用上述方法对其进行混沌特性分析.为更充分地说明风速时间序列的混沌特性, 采用不同地点、不同采样频率下的实测风速数据.下面分析的是每10 min 采样1 点的风速时间序列, 共1 500 点.如图1 所示.首先对这1 500 个风速数据进行FFT 变换得平均周期P=139(23 .2 h);然后由C-C 方法计算延迟时间τ=21 ,嵌入窗宽τw=165,并得出嵌入维数m=9 ;再根据G-P 算法求出饱和关联维ds和相应的最小嵌入维数mc ,图2 和图3 分别为lnCn(r)-lnr关系曲线和关联维数d(m)随m的变化曲线;最后据小数据量改进算法, 计算得到最大Lyapunov 指数λ1=0 .017 1 .这与由Wolf 方法计算得出的λ1=0 .020 5相差不大,但其耗时仅为后者的一半.图4a 为实验中风速时间序列的频谱图,图4b 为风速时间序列相空间重构向量的3 个分量x1,x2和x3的三维相图.

由图2 可以看出,随着嵌入维数m的增加,曲线趋于饱和.由图3 可以确定, 饱和关联维数ds=4 .357 8和最小嵌入维数mc =6 .这说明风速时间序列有分数维吸引子存在.这是混沌系统的一个典型特征.由图4 可以看出, 谱图连续且变化较为剧烈,并且相图与随机序列的相图存在较大差异(随机序列点均匀一致地几乎填满整个相空间).图4 表明,风速时间序列不是简单的周期序列, 而是复杂的非线性序列, 相空间图的复杂形状暗示风速序列可能存在混沌.通过对最大Lyapunov 指数λ1的计算, 得出λ1＞0 的结论, 说明风电场风速具有混沌特性.正是这种混沌特性,使风速吸引子在相空间中拉伸、折叠或回转, 在时间序列上呈现出一定的不规则、貌似随机等特点,但其内部又遵循着一定的规律性.

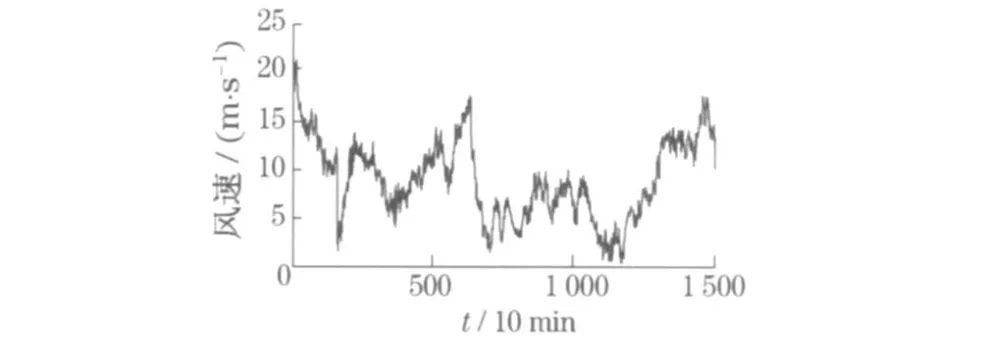
图1 风电场风速时间序列(实例一)Fig .1 Time series of wind speed in wind farm(example 1)

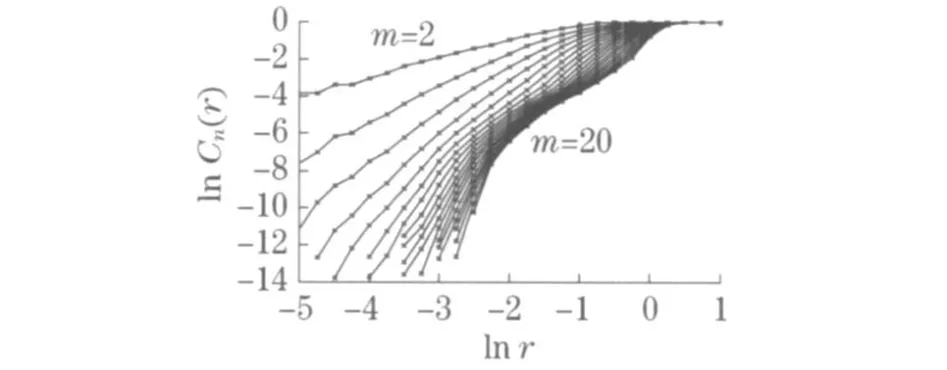
图2 lnC n(r)-lnr 关系曲线(实例一)Fig.2 Curves of lnC n(r)-lnr(example 1)

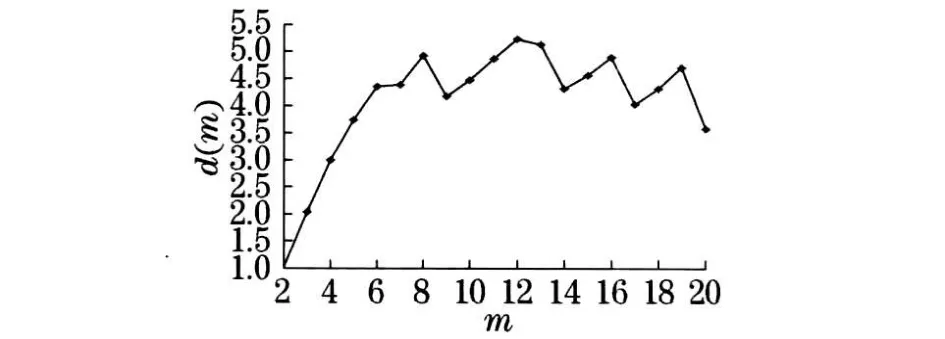
图3 d(m)-m 关系曲线(实例一)Fig .3 Curve of d(m)-m(example 1)

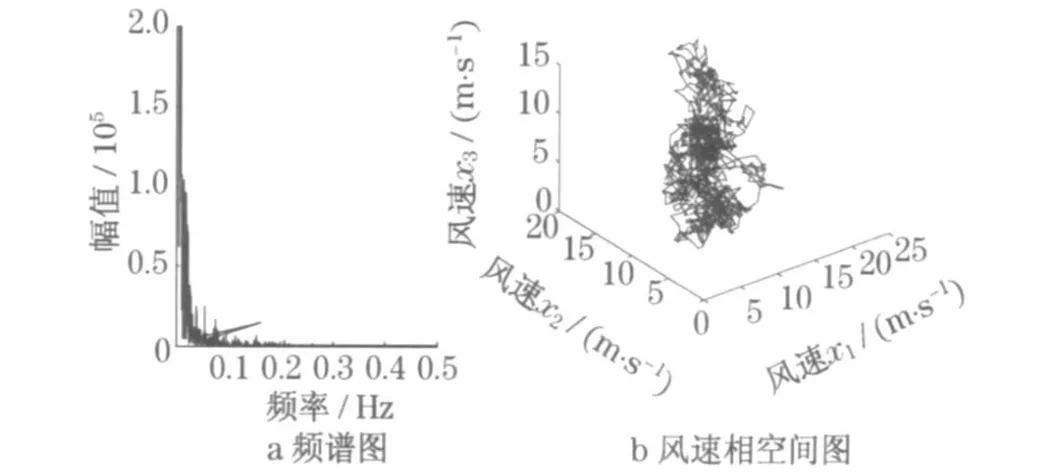
图4 风速时间序列频谱图和相空间图Fig .4 Freq-power and phase diagram of wind speed

2.2 实例分析二

下面对每1 小时采样1 点的风速时间序列实测数据进行分析.如图5 所示, 共601 点按照上述方法,先进行FFT 变换,得平均周期P=26 h(与例一的结果十分接近);然后由C-C 方法计算出延迟时间τ=11 ,嵌入窗宽τw=57 ,并得出嵌入维数m=6 ;再据G-P 算法, 求出其饱和关联维ds=4 .213 6 ,相应的最小嵌入维数mc=5 ,图6 和图7 分别为lnCn-lnr关系曲线和关联维数d(m)随m的变化曲线,由图6 可以看出, 随着嵌入维数m的增加,曲线同样也趋于饱和, 说明了风速时间序列分数维吸引子的存在;最后, 根据小数据量改进算法计算得到最大Lyapunov 指数λ1=0 .075 5 ＞0 (由Wolf 方法计算得出的λ1=0 .084 2), 这些参数均能表明风电场风速确实具有混沌特性.

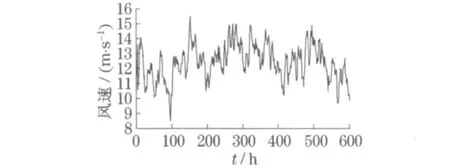
图5 风电场风速时间序列(实例二)Fig .5 Time series of wind speed in wind farm(example 2)

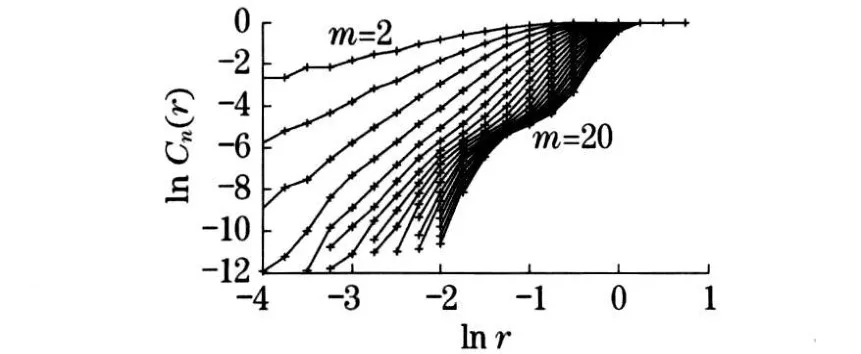
图6 ln C n(r)-ln r 关系曲线(实例二)Fig.6 Curves of ln C n(r)-ln r(example 2)

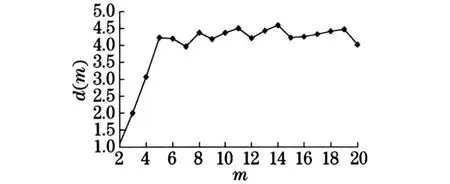
图7 d(m)-m 关系曲线(实例二)Fig .7 Curve of d(m)-m(exam p le 2)

3 结语

通过选取合适的混沌特征参数计算方法, 只需相对较小的计算量, 即可实现某大型风电场不同地点、不同采样频率下的实测风速数据的混沌分析.实验结果证实了风速时间序列具有混沌系统的典型特征,为正确掌握风速的演变规律具有重要意义,对提高风速本身和风电场发电功率的预测精度具有重要的指导作用.

[1] 杨秀媛, 梁贵书.风力发电的发展及其市场前景[J] .电网技术, 2003, 27(4):77.YANG X iuyuan, LIANG Guishu.Development of wind power generation and its market prospect [J] .Power System Technology,2003, 27(4):77.

[2] 雷亚洲, 王伟胜, 戴慧珠, 等.风电对电力系统运行的价值分析[J] .电网技术, 2002, 26(2):10.LEI Yazhou, WANG Weisheng,DAIHuizhu, et al.Analysis of wind power value to wind power operation[J] .Power System Technology,2002, 26(2):10.

[3] Hay kin S,LI Xiaobo .Detection of signals in chaos [J] .Proceeding s of the IEEE,1995, 83(1):95.

[4] Takens F .Detecting strange attractors in turbu lence[M] ∥Lecture Notes in Mathematics.Berlin:Springer Press,1981:366-381.

[5] 冬雷, 高爽, 廖晓钟, 等.风力发电系统发电容量时间序列的混沌属性分析[J] .太阳能学报, 2007, 28(8):1290.DONG Lei, GAO Shuang,LIAO Xiaozhong,et al.Chaos characteristic analysis on the time series of wind power generation capacity [J] .ACT A Energiae Solaris SINIC A ,2007, 28(8):1290.

[6] Kim H S, Eykholt R, Salas J D.Nonlinear dynamics, delay times and embedding windows[J] .Physica D,1999, 127(1/ 2):48.

[7] Grassberger P,Procaccia I .Measuring the strangeness of strange attractors[J] .Physica D, 1983, 9 (1/2):1898.

[8] Rosenstein MT,Collins J J, De L C J.A practical method for calculating largest Lyapunov exponents from small data sets[J] .Physica D,1993, 65(1/2):117.

[9] Wolf A,Swift J B,Sw inney H L, et al.Determining Lyapunov exponents froma time series[J] .Physica D, 1985, 16(1):285.

[10] 吕金虎, 陆君安, 陈士华.混沌时间序列分析及其应用[M] .武汉:武汉大学出版社, 2002.LV Jinhu,LU Jun' an,C HEN Shihua.Chaotic time series analysis and applications [M] .Wuhan :W uhan University Press, 2002.