基于数据的建筑能耗分析与建模

刘丹丹 ,陈启军 ,森一之 ,木田幸夫

(1.同济大学电子信息工程学院, 上海201804;2.上海电力学院计算机与信息工程学院, 上海200090;3.日本三菱电机先端技术研究所, 日本 尼崎661-8661;4.日本三菱电机福山制作所, 日本 福山720-8647)

建筑能耗分析是确定合理的节能策略的基础,是节能降耗工作的研究热点之一, 国内外很多学者对于建筑能耗分析与建模方法进行了深入的研究,这些研究可分为两类.第一类研究[1-4]主要以建筑结构为研究对象, 在建筑设计阶段使用建筑能耗逐时模拟软件对于能耗进行预测.模拟软件多以热力学理论为基础, 综合考虑影响建筑能耗的多种内扰(人,使用方式等)、外扰(环境)因素, 列出热力学方程进行求解, 得出建筑在满足人的需求以及达到人体舒适度的情况下所需的能耗.代表性的软件为美国能源部主导开发的DOE-2,EnergyPlus ,中国清华大学开发的DeS T 软件等.软件模拟的方法在建筑设计阶段起到很大的辅助作用, 深入研究了建筑本身的固有特性(如结构、围护等)对能耗的影响.而在建筑使用阶段, 由于人对于建筑物的使用方式具有不确定性, 导致建筑设计中对能耗的预测分析结果与实际情况有较大区别.

而建筑能耗数据包含了建筑在运行阶段的所有信息.研究能耗数据可以了解能耗的产生规律,由此选择合理的建筑管理方案与节能策略.因此第二类研究集中在对于能耗数据的分析上.对建筑的能耗数据进行深入研究与调研, 使用线性回归算法[5-8],人工智能方法[9-10]或者数据挖掘算法[11]寻找能耗数据与影响因素之间的关系, 由此预测与分析建筑能耗.但是这些文献的研究对象一般为一个城市或一个地区的用电量, 同时大多以月耗电量或者年耗电量为研究分析对象, 对于建筑的逐时耗电量分析几乎没有涉及, 因此对于能耗规律的描述过于粗略,不能完全满足短期负荷预测的需要.

本文在对能耗数据以及建筑的运行方式深入研究的基础上, 提出了基于数据的建筑能耗的建模方法.根据不同类别能耗数据的特点的不同, 分别利用线性回归算法以及决策树算法建立了能耗模型.该模型可预测建筑的逐时能耗, 预测准确率较高.同时, 也可使用能耗模型评估建筑的管理方式对电力消耗的影响.

1 原理与方法

对建筑能耗数据分项计量, 不同类型的能耗数据具有不同的特点.因此必须选择不同的算法进行描述.

1.1 线性回归分析算法

回归分析算法是一种很实用的统计分析方法,其基本功能是研究某一变量和其他有关变量之间的依赖关系,能够根据已知信息对其建立数学模型,并利用该模型做出估计或预测.

其主要步骤为:①从一组数据出发确定某些变量之间的定量关系式, 即建立数学模型并估计其中的未知参数.估计参数的常用方法是最小二乘法.②对这些关系式的可信程度进行显著性检验.③在许多自变量共同影响着一个因变量的关系中,判断哪个(或哪些)自变量的影响是显著的,哪些自变量的影响是不显著的, 将影响显著的自变量选入模型中,而剔除影响不显著的变量.④利用所求的关系式对某一生产过程进行预测或控制[12].

1.2 决策树算法

决策树是一种从无次序、无规则的样本数据集中推理出决策树表示形式的分类规则方法.分类与回归树(classification and regression trees,CA RT)算法是一种产生二叉决策树的技术.其利用历史数据中包含的信息建立决策树, 也可利用已经建立的规则对数据进行预测.CA RT 决策树算法包括以下三个部分:

(1)建立决策树

CA RT 算法对每次样本集的划分计算Gini 系数,Gini 系数越小分裂越合理.假设样本集T中含有m类数据,则:

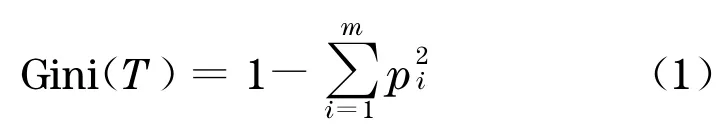
其中pi为类别Ci在T中出现的概率.若T被划分为T1和T2,则此次划分的Gini 系数为

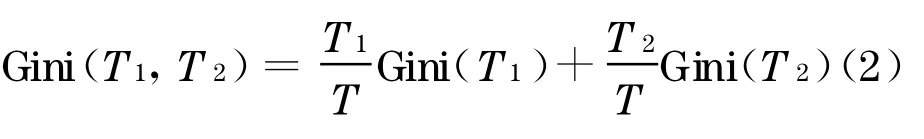
对于候选属性集中的每一个属性, CA RT 算法计算该属性上每种可能划分的Gini 系数, 并找到最小的Gini 系数作为该属性上的最佳划分, 同时CA RT 算法将比较所有候选属性上最佳划分的Gini系数, 拥有最小划分Gini 系数的属性成为最终分类的依据与规则[13].

(2)选择最佳决策树

CA RT 算法先产生最大的决策树, 而后采用交叉验证(cross validation)算法对决策树进行剪枝.该方法将训练集分为N份, 取第1 份作为测试集, 其余N-1 份作为训练集,经过一次剪枝,得到一棵局部决策树.以此类推, 直到整个模型中的N份样本集都做一次测试集为止.

(3)利用已经建立的决策树分类新的数据

利用已经建立的决策树的分类规则, 将新观测的自变量的值分配到各个终端节点上, 由此预测因变量的值.

2 建筑能耗模型的实现

2 .1 数据分析

选择一栋办公建筑为实验对象, 对该建筑的能耗数据进行了逐时分项测量, 同时也调查了建筑内的逐时办公人数以及建筑的管理与控制方式.测量的能耗数据有:办公设备能耗数据以及照明能耗数据.建筑的管理方式有以下几个特点:办公人员的办公时间不固定;照明设备除人为控制开关之外,还随太阳辐射强度的变化而自动调整照度.

图1 与图2 分别为办公设备逐时能耗数据(electricity energy consumption of office equipment ,EECO)与办公人数(number of people, PNum)逐时数据在一周之内的时序图.从图中可以看出,这些变量随时间变化的特性比较明显.同时, 在人数为零的情况下,办公设备能耗数据并不为零.这也说明某些办公设备在接入电路时,即使在未使用的情况下也会耗电,如笔记本电源等.根据数据特点,将办公设备逐时能耗数据分为“人数为零” 时产生的数据以及“人数非零” 时产生的数据两部分.“人数为零” 部分的能耗数据几乎为常数,因此仅分析“人数非零” 部分能耗的产生规律.图3 描述了该部分数据人数与办公设备能耗的相关关系.从图中可以推断,二者之间的关系为正线性关系.

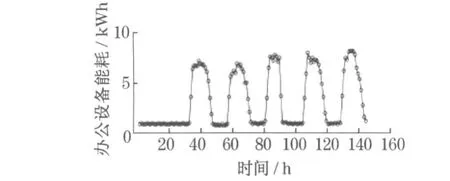
图1 办公设备逐时能耗数据时序图Fig .1 Measured hourly electricity energy consumption of office equipment over time

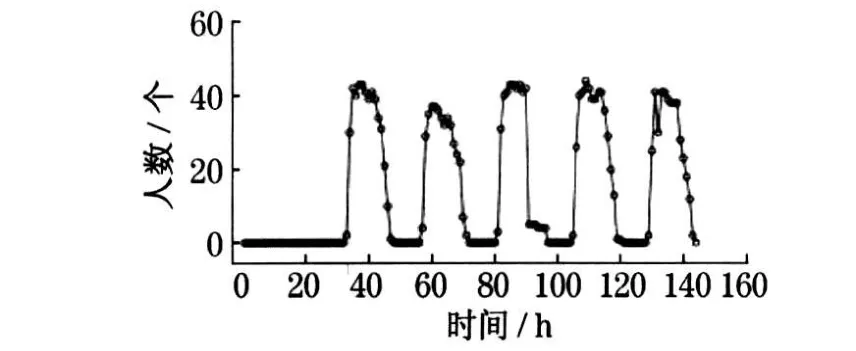
图2 办公人数时序图Fig .2 Measured hourly number of people over time

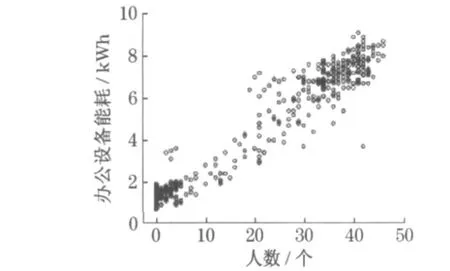
图3 办公人数与办公设备能耗的关系Fig.3 Relationship between number of people and electricity energy consumption of office equipments

图4 则表示了逐时照明能耗(lighting electricity energy consumption ,EECL)在一周内的变化趋势.根据建筑的管理方式,工作日中午12 时将会统一关闭所有照明, 但根据需要, 用户可重新打开照明设备.图5 为逐时照明能耗数据与人数的关系.与办公设备能耗不同的是, 人数多少对照明能耗有一定的影响,但当人数值大于某一个值时, 其影响变弱, 二者之间的关系明显为非线性.同时根据建筑的管理方式可知, 照明设备根据太阳辐射强度自动调整照度, 而大多数情况下太阳辐射强度在一天之内跟随时间有规律地变化.因此可认为照明能耗数据与时间有关.由此可知,该种类型的能耗数据的影响因素应为办公人数以及时间.图6 表示了三者之间的关系.

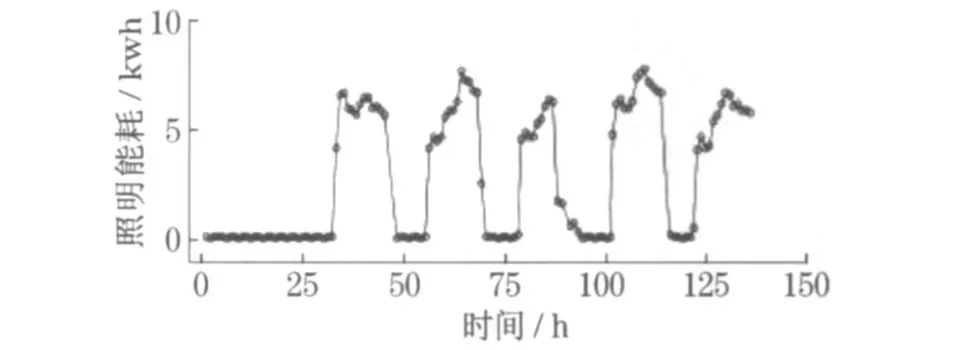
图4 照明逐时能耗数据时序图Fig .4 Measured hourly lighting electricity energy consumption over time

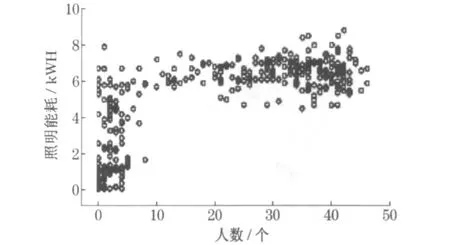
图5 照明能耗与人数的关系Fig.5 Relationship between number of people and lighting electricity energy consumption

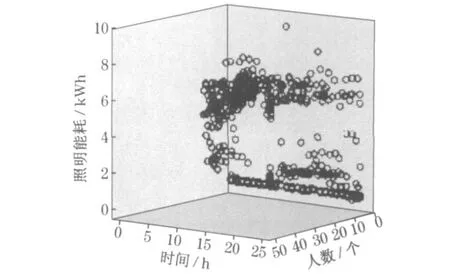
图6 照明能耗与时间以及人数之间的关系Fig .6 Relationship among number of people, time and lighting electricity energy consumption

2 .2 办公设备能耗模型

根据上文对办公设备能耗数据的分析, 线性回归算法可用以描述该类型的能耗数据.由于其“人数为零” 部分的能耗数据几乎为常数, 因此选择“人数非零” 部分的数据进行研究.选择逐时办公人数为回归模型的自变量,该线性回归方程可描述如下:

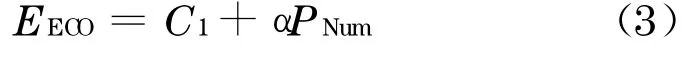
式中:EECO代表办公设备逐时能耗, kWh ;PNum代表办公人数;C1为截距;α为回归系数.

利用最小二乘法计算回归系数,C1的值为1 .459 ,α值为0 .15 .回归系数为正, 表示以上根据散点图的推断是正确的.考虑到 “人数为零” 部分的数据,回归方程可重新描述如下:

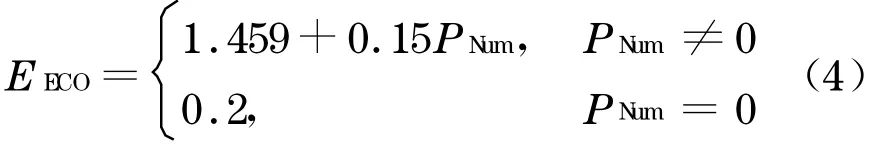
线性回归方程不能直接用于实际问题的分析,还须对该方程进行各种统计检验.本例中R2值为0 .883 ,说明办公设备能耗的88 .3 %可由自变量来解释.同时, 回归模型通过了显著水平为1 %的假设检验.而残差分析图(见图7)进一步表明了模型是可靠的.在模型通过各种检验的基础上, 利用式(4)即可预测办公设备能耗.图8 表示了预测值与实际值之间的差异.

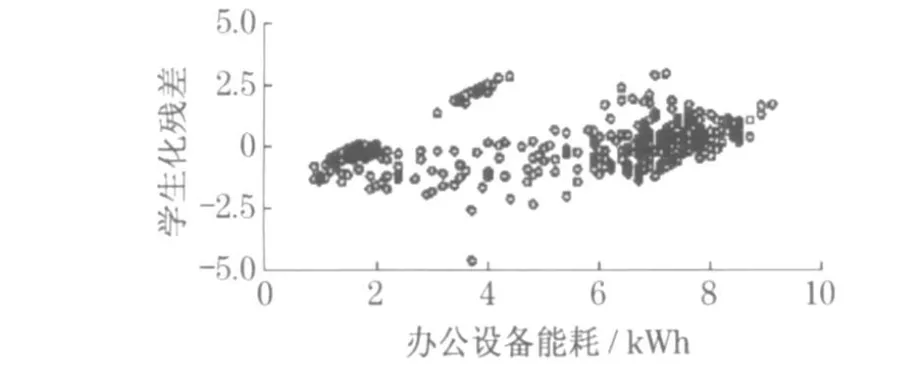
图7 办公设备能耗数据残差图Fig .7 Plot of studentized residuals

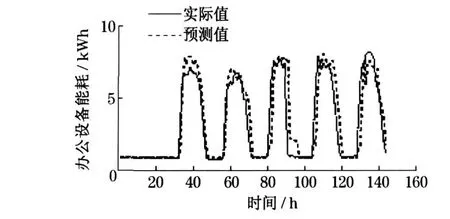
图8 办公设备能耗数据预测值与实际值的对比曲线Fig.8 Comparative curves between estimated results and real values of E ECO

采用准确率计算式(5)可进一步计算模型预测的正确率

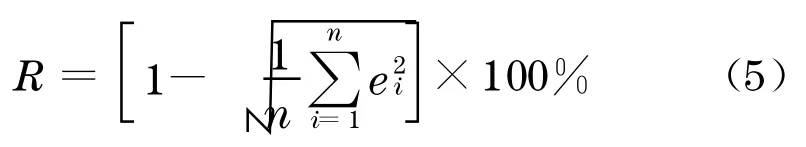
式中:R为正确率;n为样本中的数据总数;ei为文献[14] 中定义的相对误差.计算结果为预测精度等于93 %,表明该能耗模型预测准确度较高.

2 .3 照明能耗模型

根据上文描述的照明能耗数据特征, 利用CA RT 算法建立了自变量为时间与办公人数的决策树模型.以图9 为例介绍该决策树模型的建立方法.首先将时间分为两种时段:“1” 代表太阳辐射强度较弱的时段;“2” 代表太阳辐射强度较强的时段.将办公人数分为3 种类型:较多;中;较少,由此建立决策树.当太阳辐射较弱且人数较多的情况下, 照明能耗较高.当太阳辐射较强且人数较少的情况下, 照明能耗较低.其余情况下照明能耗为中等水平.

事实上,能耗决策树模型远比图9 复杂.其中时间数据为从1 到24 的整数,分别代表一天24 个小时.根据上文描述的CA RT 算法, 该回归与分类树共有8 层, 包含35 个节点,20 个终结点.表1 显示了20 类数据的基本统计特征.该20 类数据可描述如下:(1)在类15 ,22 ,31,13,29,27,28,32 及30 中,人数值为0 ,但时间属性各不相同;(2)在类25,9,35 ,38 ,26 ,37,35 及24 中, 人数较少(小于5 人),但时间属性以及电能能耗完全不同;(3)在其余类中, 人数值分布在10～45 之间,同时, 中午12 时照明数据被完全分配在数据类12 中,从另外一个侧面证明决策树方法分类数据的可靠性.

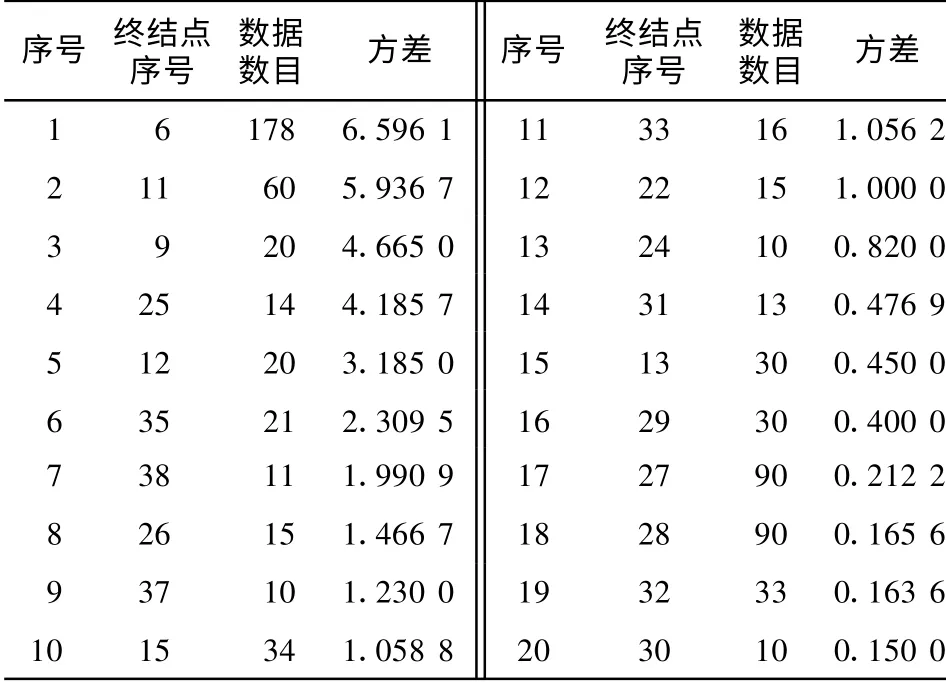
表1 各个终结点数据的统计特征Tab.1 Gain summary for nodes

用该模型预测能耗数据, 并计算模型精度.利用式(5)得到模型的预测精度为87 %.采用式(6)也可计算模型的预测精度:

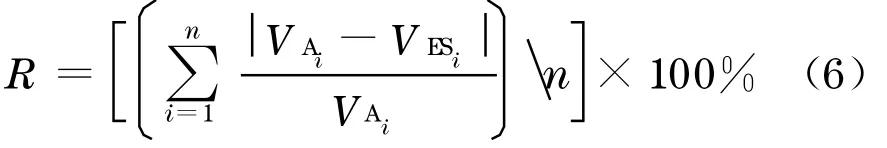
式中:VAi为第i个测量值;VESi为模型的第i个预测值;n为样本集中的数据个数.利用该公式计算模型的预测精度为92 %.这两种精度计算方法的结果都表明了模型的正确性.而图10 体现了预测值与实际值之间的相似程度.

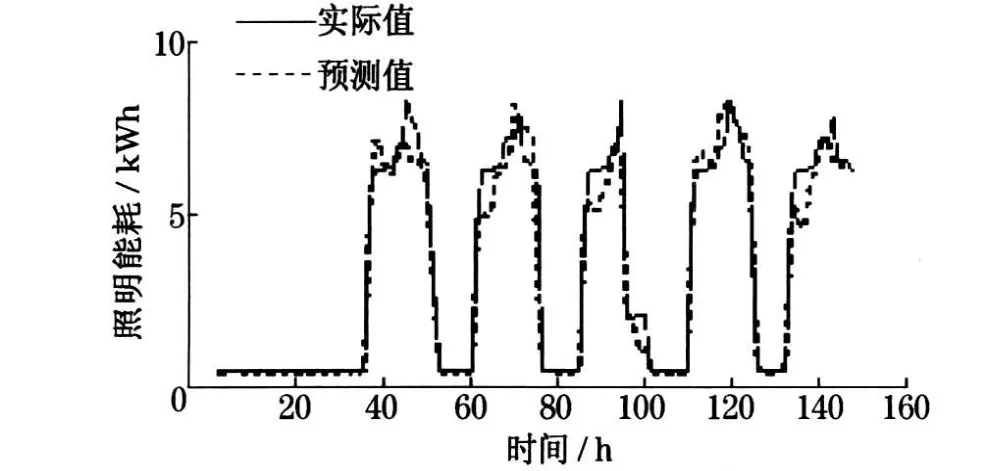
图10 照明能耗数据预测值与实际值的对比曲线Fig .10 Comparative curves between estimated results and real values of EECL

3 结论与展望

本文提出了建筑能耗数据的建模方法.从数据分析可知, 办公设备能耗数据与办公人数有较强的线性关系,可使用线性回归算法进行描述, 预测精度进一步证明了模型的正确性.而照明能耗数据的分析相对较为复杂, 其与办公人数以及太阳辐射强度都具有相关性, 并且为非线性的.在这种情况下, 可使用决策树模型描述三者之间的关系, 预测的结果表明了算法应用的正确性.

能耗数据的建模是建筑节能优化的第一步.利用该模型的预测以及分类结果可进一步研究建筑异常能耗的自动检测方法, 通过分析异常能耗的产生原因研究建筑节能策略.同时, 该模型还可评估建筑的管理模式对能耗的影响, 如模拟影响因素在不同的变化规律下的能耗状况, 有利于选择更为合理的建筑管理与控制模式, 最终达到节能的目的.

[1] Winkelmann F C .DOE-2 BDL summary (Version 21E)[Z] .Berkeley :Energy and Environment Division, Lawrence Berkeley National Laboratory,University of California, 1993.

[2] Law rence Berkeley National Laboratory,University of Illinois ,University of California.Energy plus 1.01 manual [Z] .Berkeley :Lawrence Berkeley National Laborato ry,2002.

[3] C raw leya D B,Lawrieb L K, Frederick C,et al.Energy plus :creating a new-generation building energy simulation program[J] .Energy and Building,2001, 33(4):319.

[4] C raw leya D B,Law rieb L K, Frederick C,et al.Energy plus :new capabilities in a w hole-building energy simulation program[C] ∥Seventh International IBPSA Conference .[S.l.] :Rio de Janeiro,2001:13-15.

[5] Le Com te D M, Warren H E .Modeling the impact of summer temperatures on national electricity consumption[J] .Journal of Applied Meteorol, 1981, 20(12):1415.

[6] Manish Ranjan,Jain V K.Modeling of electrical energy consumption in Delhi[J] .Energy,1999, 24:351.

[7] Lam J C,Tang H L,Li H W .Seasonal variations in residential an commercial sector electricity consumption in Hong Kong[J] .Energy,2008(33):513.

[8] Mohamed Z,Bodger P.Forecasting electricity consumption in New Zealand using economic and demographic variables[J] .Energy,2005(30):1833.

[9] Lai T M, To W M, Lo W C,et al.Modeling of electricity consumption in the Asian gaming and tourism center-Macao SAR, People' s Republic of China[J] .Energy,2008(33):679.

[10] Egolioglu F, Mohamad A A,Guven H .Economic variables and electricity consumption in North Cyprus[J] .Energy,2001, 26:355.

[11] 栗然, 刘宇, 黎静华, 等.基于改进决策树算法的日特征负荷预测研究[J] .中国电机工程学报, 2005, 25(23):36.LI Ran, LIU Yu, LI Jinghua, et al.Study on the daily characteristic load forecasting based on the optimizied algorithm of decision tree[J] .Proceedings of the CSEE,2005,25(23):36.

[12] 冯力.回归分析方法原理及SPSS 实际操作[M] .北京:中国金融出版社, 2004.FENG Li .Regression analysis method and SPSS operation[M] .Beijing :China Financial Publishing H ouse,2004.

[13] H an Jiaw ei,Kamber M.Data mining :concepts and techniques[M] .2nd ed.Beijing :China Machine Press ,2006.

[14] 牛东晓, 曹树华, 赵磊, 等.电力负荷预测技术及其应用[M] .北京:中国电力出版社, 1998.6-9.NIU Dongxiao,CAO Shuhua,ZH AO Lei, et al.T he methods and application of power sy stem load forecasting[M] .Beijing :China Electric Power Press,1998.6-9.