基于HHT 和广义Fourier 变换变频调速异步电动机故障诊断

刘振兴,李月棠,张文蓉,张雄希

(武汉科技大学 冶金自动化与检测技术教育部工程研究中心, 湖北武汉430081)

对于异步电动机的故障诊断国内外学者进行了大量的研究工作.文献[1] 统计了1999 年之前的20多年时间内在国外重要期刊和会议上发表的关于异步电动机和变频器的故障诊断论文和著作,数量达365 篇(部)之多.近年来仍有大量的文章见诸报道.

已有的方法, 如Park' s 矢量方法[2-3]、Hilbert变换方法[4-5]、双P-Q 变换[6-7]主要针对正弦波供电的非调速电机领域.鼠笼式变频调速系统具有高度的非线性、强耦合特点,在异常和故障状态下不能使用常规的简单等效和折算, 不便通过解析的方法进行分析.由于变频器输出电压的大小和频率、功率开关器件的触发角度均与运行模式有关,运行模式和故障模式的多样化, 使得常规的信号处理方法难以有效提取故障特征,难以准确地诊断故障.

在变频调速过程中, 电动机供电电源频率经常处于时变状态, 在频域表现为一段带宽;电动机转速也随时间变化而变化.由于故障成分本为微弱信号,其特征频率很容易被强大的电源信号淹没.如何消除强大的基波量的影响(尤其是断条故障特征)、突出故障特征,是诊断过程中考虑的重要问题之一.

按照变频器输出电压频率的变化规律, 变频调速异步电动机的运行模式包括恒频、频率随时间线性规律变化及其他形式.恒频(图1 中直线1)情况下与常规电源供电有相似之处, 在剔除变频器本身的谐波基础上, 可以按照常规的故障诊断方法来诊断电动机故障.频率随时间线性规律变化模式(图1 中直线2)主要应用于拖动系统的加速和减速, 也是一种常见的运行模式.本文就是针对这种情况的故障诊断进行研究.

频率随时间线性规律变化, 称为线调频运行模式.频率变化规律可以表述为

式中:f0为初始变化频率;k为频率随时间的变化比例.

为了突出故障特征,希望将在f-t平面按照线调频规律变化的电源频率f1转换到新的f′-t′平面(见图1),使电源电压频率在新的时频域中表现为恒定频率f0 .为此,针对变频调速异步电动机系统常见的恒加速和恒减速运行模式, 拟采用HHT(Hilbert-Huang transformation)变换进行运行模式辨识,在获取运行模式的基础上采用广义Fourier 变换,将线调频的电源信号转换为恒频信号,以突出故障特征.

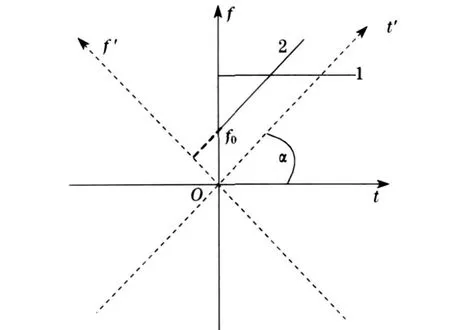
图1 频率随时间变化规律Fig .1 The linear frequency vary pattern with time

1 HHT 变换和广义Fourier 变换原理

1.1 HHT 变换原理

HHT 变 换[8]包括 EMD (empirical mode decomposition)分析方法和Hilbert 变换.通过对原始信号x(t)进行EMD 分解, 得到一系列每一点只有一个瞬时频率的本征模式函数(intrinsic mode function,IMF)单组分序列{ci(t)}和一个残差分量之和,即

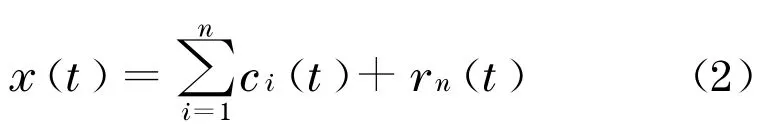
式中,rn(t)称为残余函数, 代表信号的平均趋势.

Hilbert 变换定义为

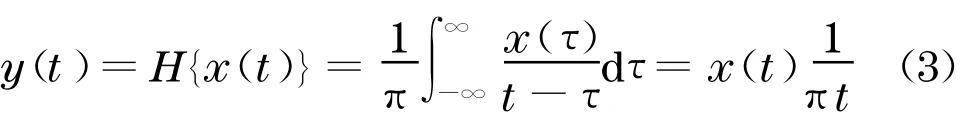
对每个IMF 序列ci(t)=xi(t)实施Hilbert 变换,得到相应的y i(t),由xi(t)与y i(t)可组成一个解析信号z i(t)

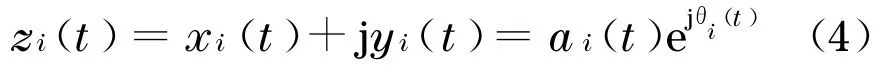
式中:i表示序数;j 为复数运算.

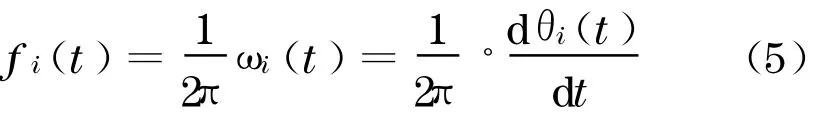
这里省略了残余项rn(t).把式(1)～(4)所表示的变换用于每个本征模态函数序列,可得

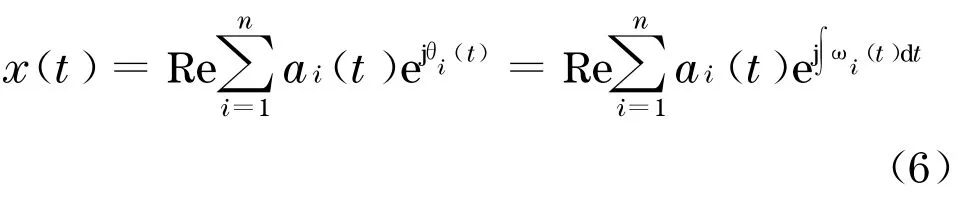
展开式(5)称为Hilbert 幅值谱, 简称Hilbert谱,记作

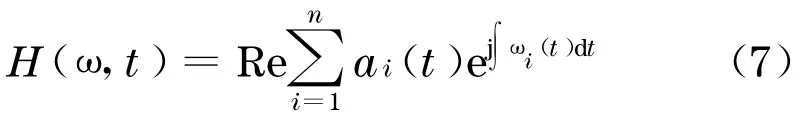
用Hilbert 谱可以进一步定义边际谱

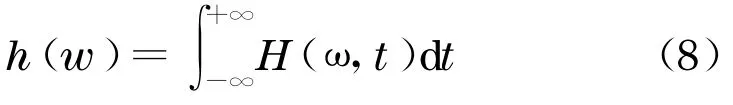
这样, 得到了瞬时频率和幅值, 即可描绘出原始信号的时频图、Hilbert 谱以及边际谱图.

1 .2 广义Fourier 变换原理

对于信号x(t),其广义傅里叶变换[9]定义为

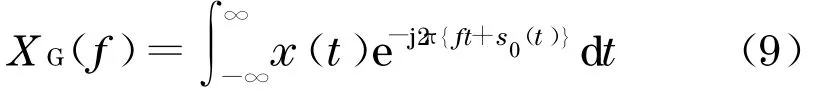
式中,s0(t)是随着时间变化的实值函数,这实际上是对x(t)e-2πS0(t)做标准的傅里叶变换, 同样可以对XG(f)进行逆广义傅里叶变换,得到x(t),即

如果XG(f)=δ(f-f0), 则有x(t)=ej2π{f t+s0(t)}.也就是说,一个瞬时频率为f(t)=f0+s′0(t)的信号, 经过合适的广义傅里叶变换, 其能量集中于频率f=f0上,其中

因此, 对于x(t),在时频相空间里其时频分布为由f0+s′0(t)确定的曲线, 如果能识别出信号频率随时间的变化规律s′0(t), 即可得到广义Fourier域的时频分布为平行于时间坐标轴的直线, 这就是图1 所对应的频率转换思想.实现广义Fourier 的关键是获取s′0 (t), 也就是频率随时间变化的规律, 这可以通过对HHT 获取的时频变化曲线的识别得到.

2 应用

理论和实验已经证明, 在恒频正弦波供电情况下, 鼠笼式异步电动机转子断条和偏心故障时的主要特征频率成分为

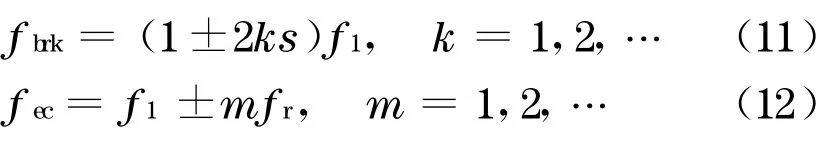
式中:f1为电动机供电电源频率;s=(n1-n)/n1,为转差率,n1为同步转速,n为电动机转子转速;fr为转子旋转频率.

当处于变频调速状态时, 电源频率随时间变化,不再是单一频率成分,转子转速也随时间改变, 故障特征频率成分会被电源频率成分“淹没”.如能将随时间变化的电源转换为恒频成分, 可以克服电源的影响,突出故障特征.

为此,对变频器输出电压或电流使用HHT 方法进行EMD 分解, 由自适应得到IMF 分量, 结合Hilbert 谱分析, 提取信号的瞬时频率,通过识别,即可确定运行模式.同时得到实施广义Fourier 变换所需要的s′0(t),从而获得s0(t).

3 仿真

假设某电动机在变频调速过程中变频器输出频率变化规律为

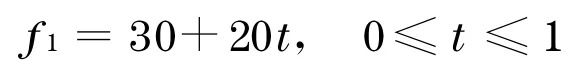
下面对正常情况下鼠龙式异步电动机转子断条、气隙偏心等行为进行仿真分析.

3.1 正常情况下的仿真

设变频器输出电流“基波”(主分量)表达式为

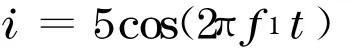
利用HHT 变换获得的三维谱、时频谱和边际谱如图2 所示.从图中可以看出, 频率的线性变化规律特征明显,可以通过辨识确定, 从而得到需要的相位函数s0(t).(此处应为s0(t)=20t2).根据获取的s0(t),进行广义傅里叶变换, 获得的三维谱、时频谱和边际谱(如图3 所示).在新的时频域中, 线调频信号成为了单一恒频成分.

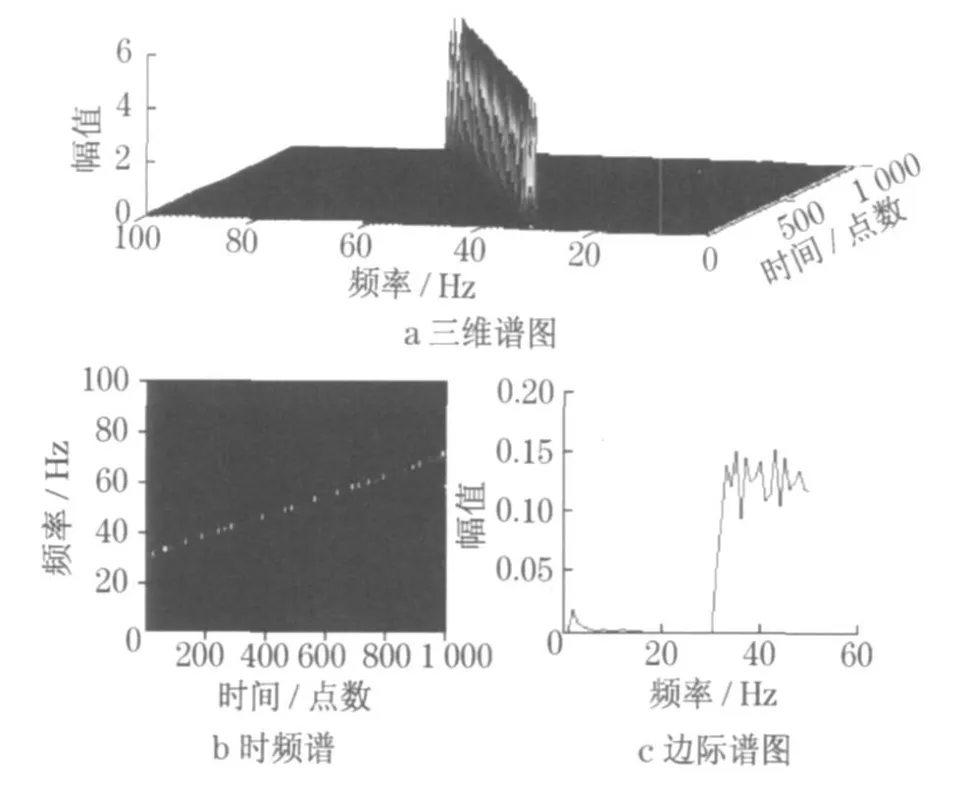
图2 频率随时间线性变化时的时频分布和边际谱Fig .2 Tim e-frequency distribution and marginal spectrum under linear frequency

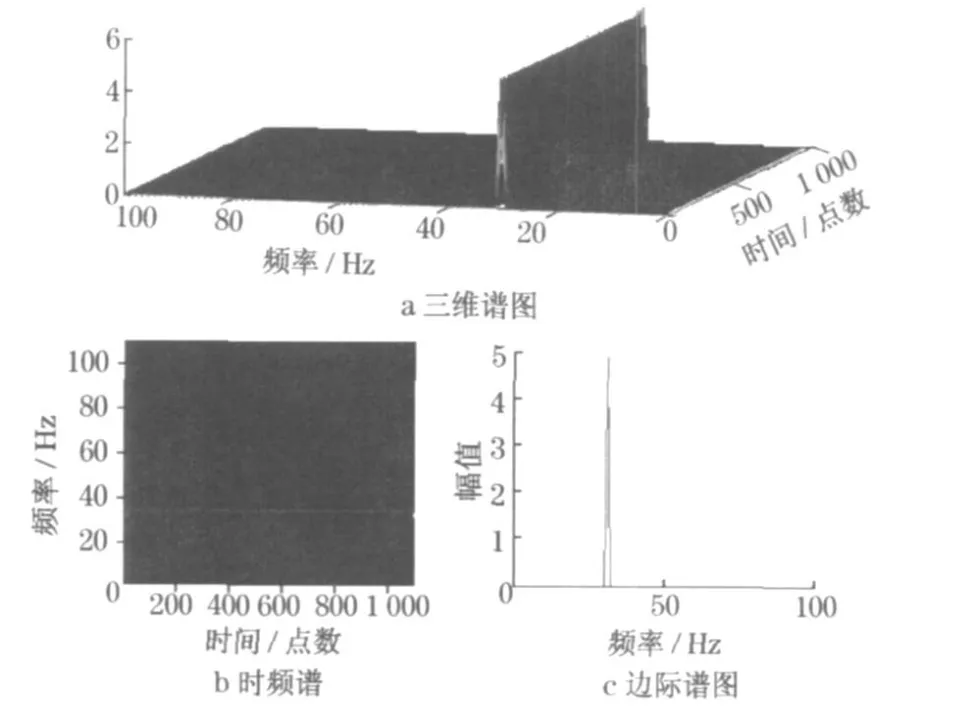
图3 经广义Fourier 变换后的频率分布和边际谱Fig .3 Tim e-frequency distribution and marginal spectrum after the generalized Fourier transform

3.2 鼠笼式电动机转子断条故障时的仿真

转子存在断条故障时,主要出现频率fbrk=(1 ±2ks)f1 的特征成分, 尤其以k=1 时的频率成分明显.为此,可假设相电流为线调频加速情况下, 电动机以最大转矩拖动负载运行,如果负载为恒转矩性质,转速线性增加.

利用HH T 变换获得的三维谱、时频谱和边际谱如图4 所示.由于频率成分的复杂性,难以体现出故障特征.进一步施加广义傅里叶变换,获得的三维谱、时频谱和边际谱如图5 所示.电源转换为恒定频率分量, 与图4 比较可以看出, 有故障频率出现, 边际谱曲线简洁, 有利于突出故障特征.

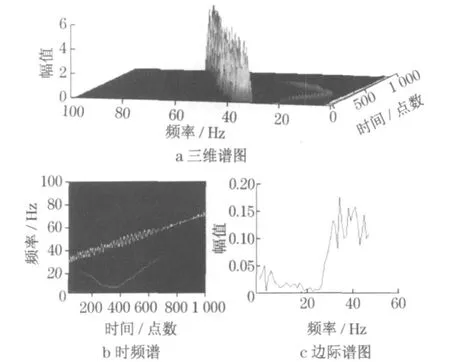
图4 频率随时间线性变化转子断条时的时频分布和边际谱Fig .4 Tim e-frequency distribution and marginal spectrum with broken rotor bar

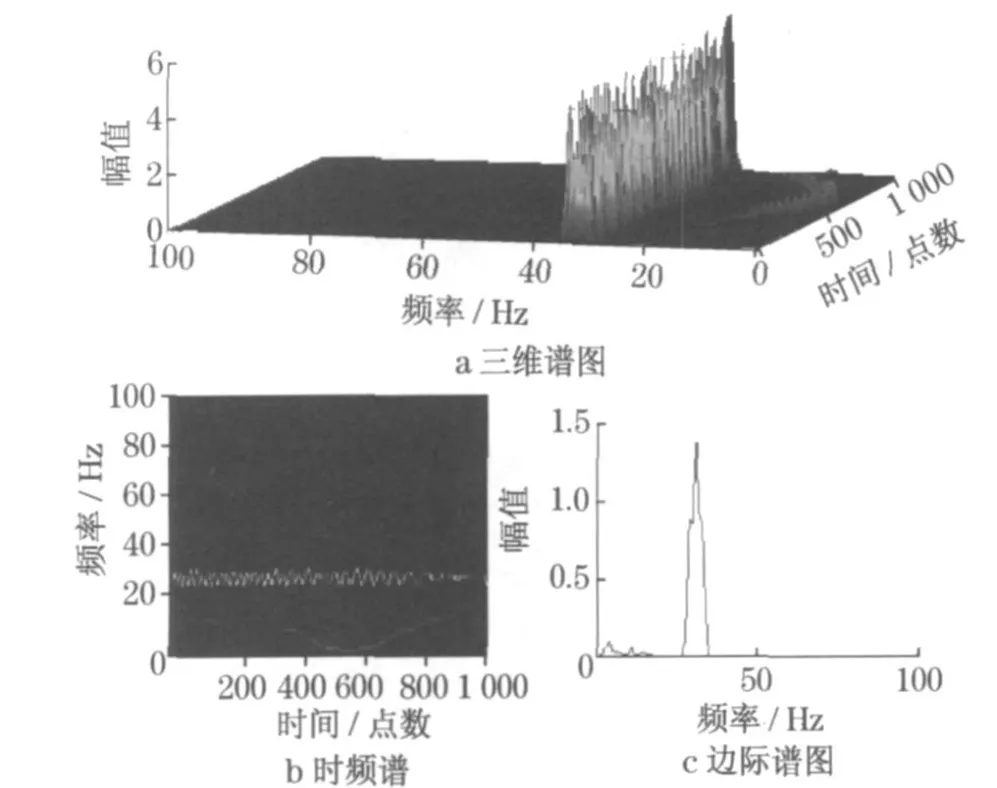
图5 断条情况下经广义Fourier 变换后的频率分布和边际谱Fig .5 Tim e-frequency distribution and marginal spectrum with broken rotor bar after the generalized Fourier transform

3.3 鼠笼式电动机转子偏心故障时的仿真

当电机中存在偏心故障时, 定子电流中会感应出f1±m fr的故障频率分量, 尤其以m=1 时的频率成分明显.假设相电流为

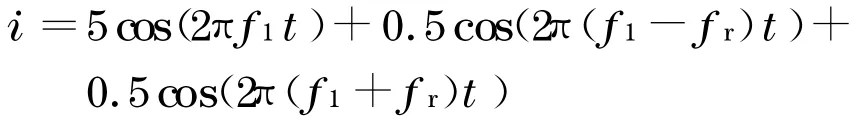
利用HHT 变换获得的三维谱、时频谱和边际谱如图6 所示, 采样信号谱图没有理想的信号谱图“干净” .施加广义傅里叶变换, 获得的三维谱、时频谱和边际谱如图7 所示, 电源转换为恒定频率分量,与图6 进行比较,同样可看出有故障频率的出现.与图5 进行比较, 不同故障所得的边际谱图中的频率变化规律有所差别, 边际谱曲线简洁,同样可以突出故障特征.

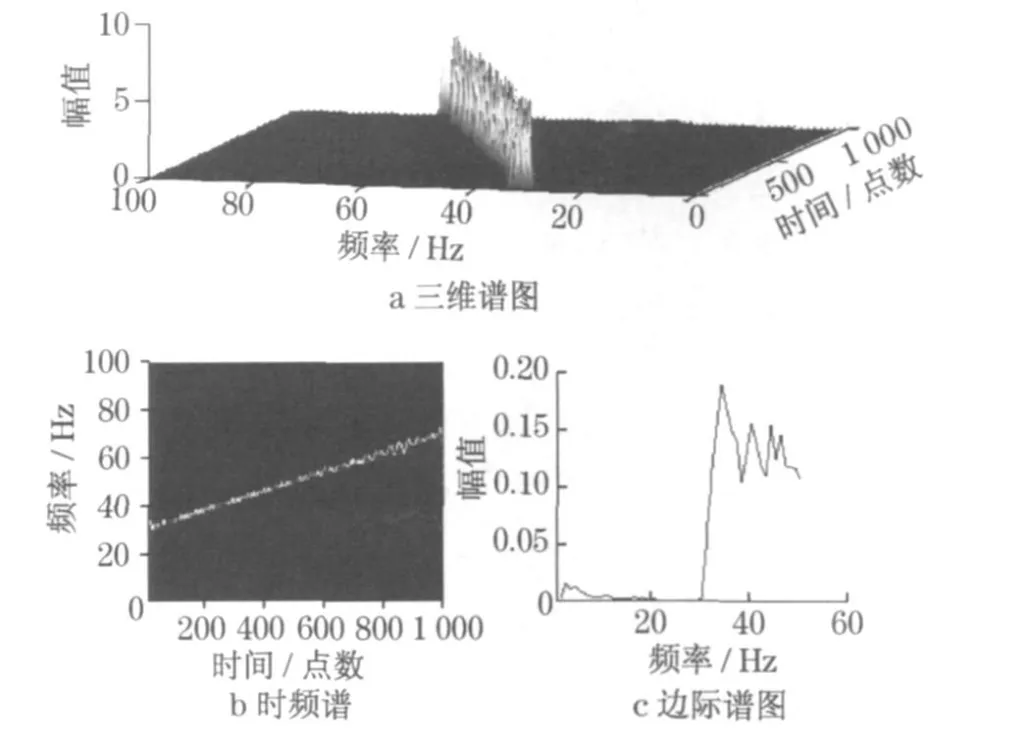
图6 频率随时间线性变化转子偏心时的时频分布和边际谱Fig .6 Tim e-frequency distribution and marginal spectrum with rotor eccentricity

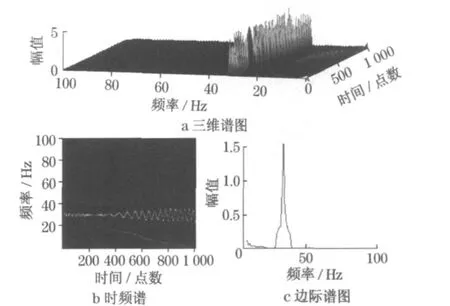
图7 偏心情况下经广义Fourier 变换后的频率分布和边际谱Fig .7 Tim e-frequency distribution and marginal spectrum with rotor eccentricity a fter the generalized Fourier tran sform

4 结语

本文提出了一种基于HHT 变换和广义Fourier变换的变频调速异步电动机故障诊断方法.对变频调速异步电动机的电流信号通过HHT 变换, 可以获取电源主成份频率随时间变化的规律及相应的广义Fourier 变换所需要的时频转换函数;进一步通过Fourier 变换可以将电源主成份转换成新的时频域的恒频成分,可以突出故障特征.仿真结果表明, 该方法效果良好.由于仿真是在理想环境下实施的, 实际的变频器输出电压和电流谐波成分复杂, 且运行方式多样,需要提取其主分量并经过识别以确定运行模式.故故障特征及其量化指标等还有待进一步深入研究.

[1] Benbouzid ME H .Bibliography on induction motors faults detection and diagnosis[J] .IEEE Transactions on Energy Conversion, 1999, 14(4):1065.

[2] C ruz S MA,Cardoso A J M.Rotor cage fault diagnosis in three-phase induction motors by Ex tended Park' s Vector approach[J] .Electric Machines and Power Sy stems, 2000, 28(4):289.

[3] 侯新国, 吴正国, 夏立.基于Park 矢量模平方函数的异步电动机转子故障检测方法研究[J] .中国电机工程学报, 2003, 23(9):137.HOU Xinguo ,WU Zhengguo, XIA Li.Amethod for detecting rotor faults in asynchronous motors based on the square of the Park' vector modulus[J] .Proceeding of the CSEE,2003, 23(9):137.

[4] 邱阿瑞.提取感应电动机转子故障特征的新方法[J] .清华大学学报:自然科学版, 1997, 37(1):35.QIU Arui.New approach of extracting rotor fault feature in induction motors[J] .Journal of Tsinghua University :Natural Science,1997, 37(1):35.

[5] LIU Zhenxing ,ZH ANG Xianglong,YIN Xianggen, et al.Rotor cage fault diagnosis in induction motors based on spectral analy sis of current Hilbert modulus[C] ∥2004 IE EE Power Engineering Society General Meeting .Denver :Institute of Electrical and Electronics Engineers Inc., 2004:1500-1503.

[6] 黄进, 牛发亮, 杨家强.基于双PQ 变换的感应电机转子故障诊断[J] .中国电机工程学报, 2006.26(13):135.H UANG Jin, NIU Faliang,YANG Jiaqiang .Rotor faults diagnosis for induction moto rs based on the double PQ transformation [J] .Proceeding of the CSEE,2006, 26(13):135.

[7] 黄进, 牛发亮, 杨家强.考虑负荷及惯量影响的感应电机转子故障诊断[J] .中国电机工程学报, 2006,26(14):120.H UANG Jin, NIU Faliang,YANG Jiaqiang .Rotor faults diagnosis for induction motors considering effects of the load and inertia[J] .Proceeding of the CSEE,2006, 26(14):120.

[8] Huang N E,Shen Z .T he empirical mode decomposition and the hilbert spectrum for non-linear non-stationary time series analysis[C] ∥Proceedings of the Royal Society of London.Series A :Mathematical, Physical and Engineering Sciences .London:T he Royal Society Press, 1998:903-995.

[9] 杨宇, 程军圣, 于德介.广义解调时频分析方法中的若干问题探讨[J] .振动与冲击, 2008, 27(2):19.YANG Yu, CH ENG Junsheng,YU Dejie .Study on some problems in the generalized demodulation time-frequency analy sis method[J] .Journal of Vibration and Shock, 2008, 27(2):19.