例谈变式在初中数学教学中的作用

● (大麻镇中心学校 浙江桐乡 314514) ● (邵逸夫中学 浙江桐乡 314511)

例谈变式在初中数学教学中的作用

●徐利国(大麻镇中心学校 浙江桐乡 314514) ●许伟龙(邵逸夫中学 浙江桐乡 314511)

所谓变式，就是在引导学生认知事物属性的过程中，不断变更所提供的直观材料或事例呈现的形式，使事物的非本质属性时隐时现，而本质属性保持恒定.在新课程实施过程中，初中数学教学的主要任务还是让学生掌握数学基本知识、基本技能、基本的数学思想及对运算能力、空间想象能力、逻缉思维能力、分析与解决问题能力等的培养.教师要充分利用变式进行变式训练，有意识地把教学过程变为数学思维活动的过程，从而提高学生的解题能力.

1 在命题中变式

在多前件的命题中，把后件与前件作一对一的交换，得到的新命题被称之为偏逆命题.根据逻辑关系，当原命题为真时，偏逆命题则恒真.根据这一特点，可编撰很多题目.

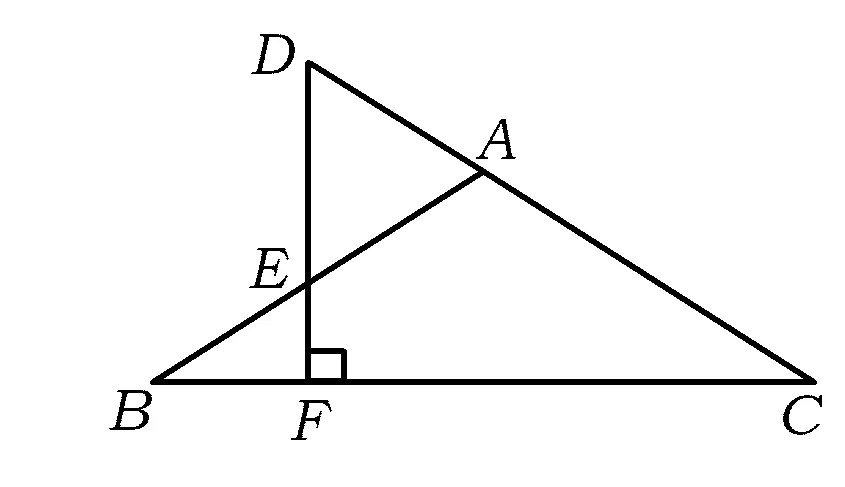
图1

例1已知：如图1所示，在△ABC中，AB=AC，DF⊥BC于点F，交AB于点E，交CA的延长线于点D.求证：AD=AE.

变式1如图1，在△ABC中，DF⊥BC，交AB于点E，AD=AE.求证：AB=AC.

变式2如图1，在△ABC中，AB=AC，DF交AB于点E，交CA的延长线于点D，AD=AE.求证：DF⊥BC.

深度思考

我们发现，通过对命题前、后件的交换，可以让学生多角度获得变式知识，多感观获得变式体验.变式是手段，提升是目的.在变式与提升之间，建立起必然联系就是数学思维.

变式是学生主体在教学活动中个性化的感受，这种感受的最初形态是凌乱、感性的，要成为学生个体的知识还需要有一个内化的过程，需要进行自我建构，自主地对感性状态的变式体验进行归纳、整合，获得对表象性的体验的深度认识.因此，对数学变式思考的深入，能让学生将粗浅的知识升华，让学生的数学思维走向深刻.

2 在集合中变式

已知全集U，欲求子集A，如果直接求A比较麻烦，那么可考虑先求的补集CUA，再求A=CU(CUA).其实质是通过2次否定实现一次肯定，这也是哲学思想上的否定之否定规律在数学中的具体表现.因此，在解此类题目有困难时，可以充分利用这个特点，转变思路，从补集的角度入手.

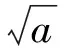
分析“至少有1个方程有2个不相等的实数根”包含着3种情况，分别讨论较繁.而通过补集概念来证明非常简单，因为它的反面只有一种情况，即“没有一个方程有2个不相等的实数根”.

证明假设在3个方程中没有一个方程有2个不相等的实数根,则3个方程的判别式

Δ1≤0，Δ2≤0，Δ3≤0，

于是

因为

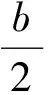
所以

由于a,b,c均为正数，因此

这与式(1)矛盾.故假设“在3个方程中，没有一个方程有2个不相等的实数根”是错误的，从而原命题结论正确.

深度思考

郑毓信教授曾说过：“知识求连，方法求变.”学生的认知发展是有规律的，变式教学是学生获取解题方法的有效途径.张光鉴在《相似论》中指出，如果在问题求解时，某个偶然的机会，相似块与问题求解的信息度达到高度的相似结合与相似匹配，产生了某种共振状态，信息的幅度就会大大增加.因此，在某种意义上说，变式教学的过程就是相似信息的共振过程，或者说是由相似信息的共振引起的.这样的教学设计完全摆脱了学生机械地判断，可以优化学生的思维品质，从而促使学生数学思想的发展.

3 在证明中变式

有些数学问题直接从已知出发进行推理，能得出的结论甚少,此时可以用间接的证法——反证法证明.当然，用反证法要考虑清楚原结论的反面，掌握证明适用的范围.

例3已知凸四边形ABCD,求证：这个凸四边形一定可以被分别以AB，BC，CD，DA为直径的半圆所覆盖.

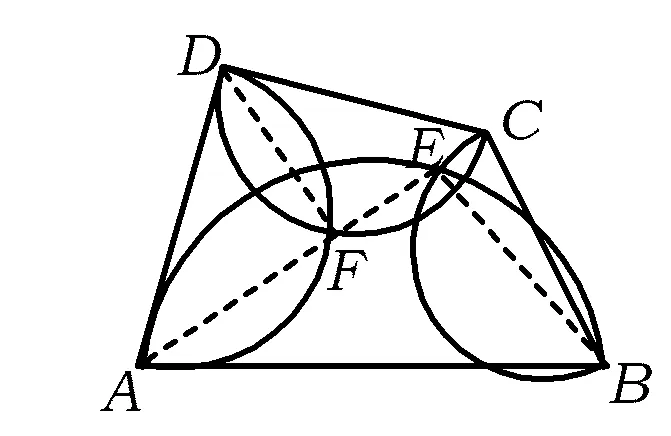
图2

分析如图3，由半圆可以想到以AB，BC，CD，DA为斜边的直角三角形.连结AC，作DF⊥AC于点F，BE⊥AC于点E，则四边形ABCD被4个直角三角形△ABE，△BCE，△CDF，△ADF所覆盖.因为以AB，BC，CD，DA为直径的4个半圆分别覆盖4个直角三角形，所以这4个半圆覆盖四边形ABCD.

这就是正面的思考，主体工作已经完成，需要细致思考的是点E,F可能在AC的延长线上，如图3或图4所示，结论也成立.此时，对比下面的反证法可知，反证法显得更紧凑、有力.

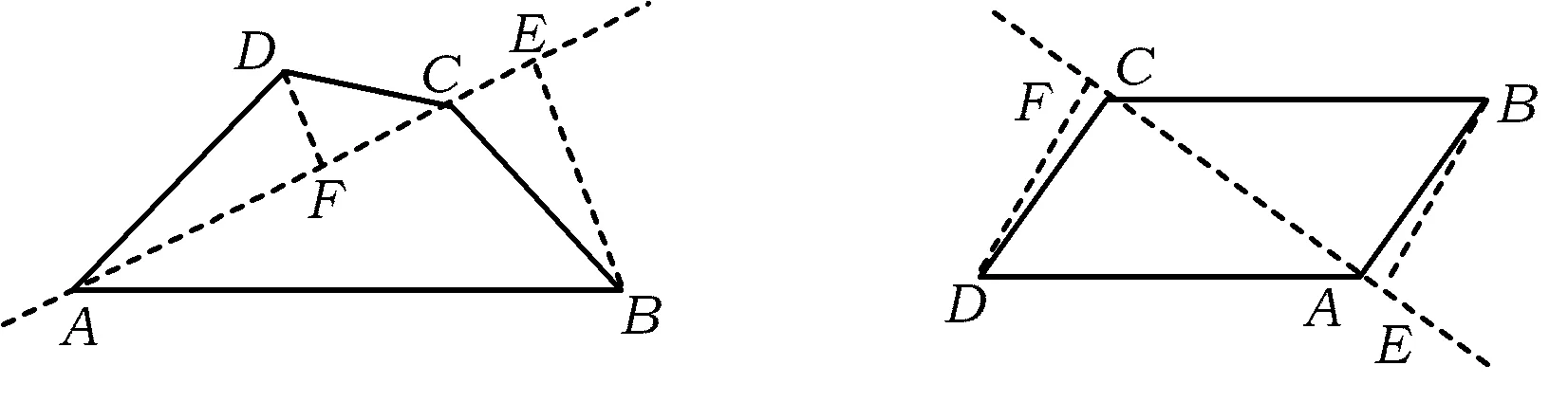
图3 图4

证法1以AB，BC，CD，DA为直径在四边形内作4个半圆.设点P为四边形ABCD内一点，若点P不被这4个半圆的任一个覆盖，则在4个半圆之外.连结PA，PB，PC，PD，则

∠APB<90°，∠BPC<90°，

∠CPD<90°，∠DPA<90°,

相加得

360°=∠APB+∠BPC+∠CPD+∠DPA<360°.

这一矛盾说明，点P必被某一半圆所覆盖.

这个证法的关键是利用了圆周角等于360°，若先使用这一知识，把推理反过来，又得出一个正面证法.

证法2取四边形ABCD内一点P，连结PA，PB，PC，PD,则∠APB，∠BPC，∠CPD，∠DPA中的最大角必非锐角.记∠APB≥90°，则点P被以AB为直径半圆覆盖.

以上说明，若经常利用变式的思维，则可以使命题的证明更有力，同时也可以提升学生解题能力的层次.

深度思考

数学教学离不开反面猜想，反面猜想是一种难度较大的跳跃性的创造性思维，是人的思维在已有事实和经验上，运用非逻辑手段而得到的一种合理的假设推理.在数学的发展史上，有使用反证法的不少典范，学生应该掌握这一基本的证法.在数学教学中，这样的教学设计可以让学生在正面与反面的强烈反差中产生一种震撼，经历此心理活动后往往会给学生留下深刻的印象，从而强化对变式观念的建立.

4 在习题中变式

课本习题中有许多基本的题目，只要仔细挖掘，就能让学生得到变式的训练.

课例4如图5，A，B，C，D这4个点在一条直线上，问图中有几条线段？是哪几条？

解从左到右找线段，以A为起点的线段有AB，AC，AD这3条，以B为起点的有BC，BD这2条，以C为起点的有CD一条，因此图5中共有线段3+2+1=6条.

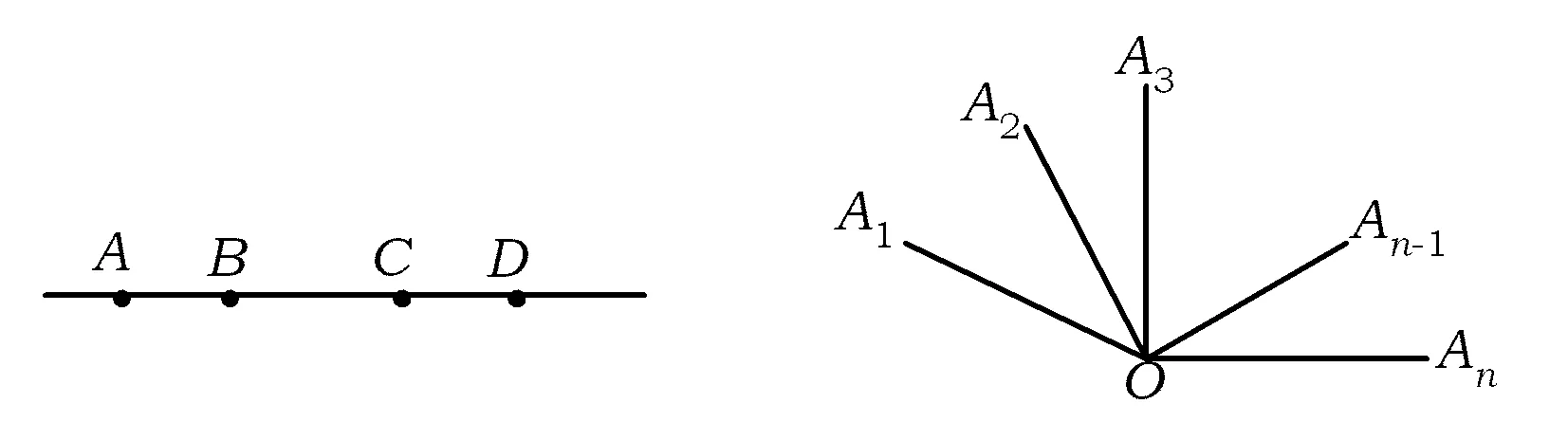
图5 图6

此题有以下多种变式：

(1)数线段：一条线段上有n个点A1,A2,A3,…,An，以任意2个点为端点的线段共有多少条？

解在直线上依规律从左到右找线段，以A1为端点的有(n-1)条,以A2为端点的有(n-2)条，以A3为端点的有(n-3)条,…,以An-1为端点的有1条.因此，共有线段

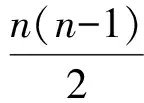
(2)数角：如图6，同一平面上有个n个点A1,A2,A3,…,An，以O为端点作射线OA1,OA2,OA3,…,OAn，则图中共有多少个角？

解在射线上依规律从左到右，以OA1为始边的有(n-1)个角，以OA2为始边的角有(n-2)个，以OA3为始边的角有(n-3)个,…,以OAn-1为始边的角有1个.因此，图中共有角

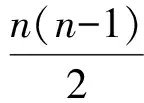
(3)数三角形：如图7所示，一条直线上有n个点A1,A2,A3,…,An，点O是直线外一点，顺次连结OA1，OA2，OA3,…,OAn，则图中共有多少个三角形？

解在直线上依规律从左到右找线段，以点A1为端点的有(n-1)条,以点A2为端点的线段有(n-2)条，以点A3为端点的线段有(n-3)条,…,以点An-1为端点的线段有1条.因此，图中共有三角形

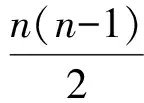
(4)数平行四边形.

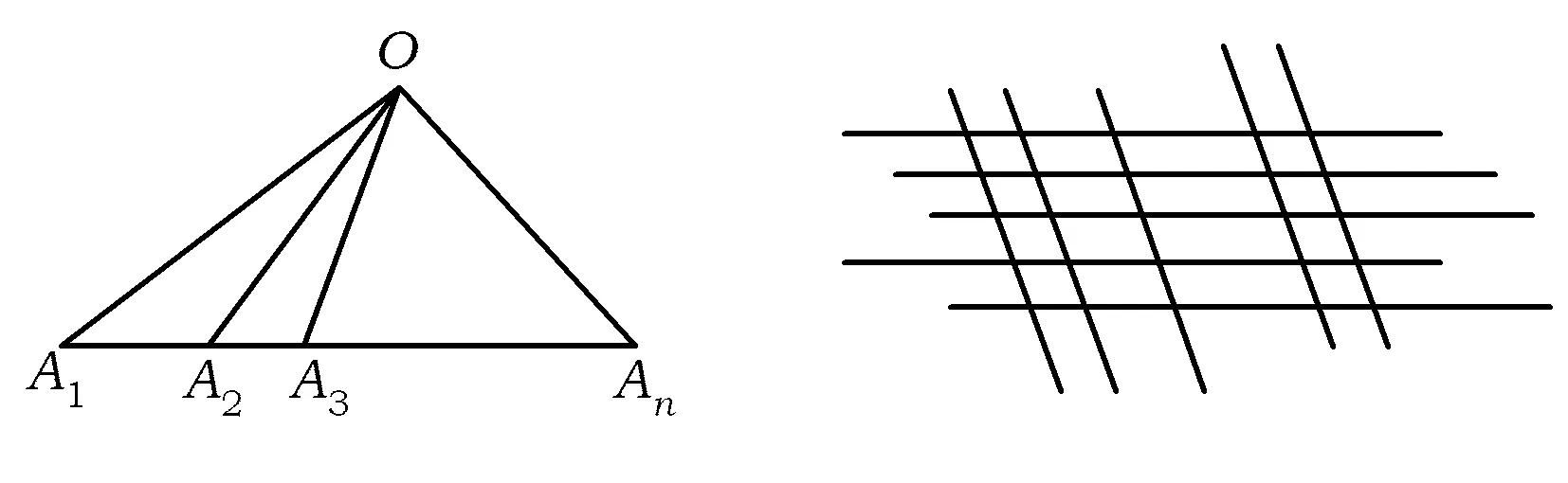
图7 图8

①现有纵、横2组平行线相交，每组5条，如图8，则图中有多少个平行四边形？

解因为每一条直线与一组平行线相交可得5个点，所以平行四边形有

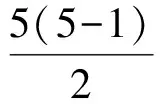
②纵、横2组平行线相交，如果纵向有m条，横向的有n条，那么这2组平行线可构成多少个平行四边形？

解因为横向上每条直线被纵向上的平行线截为m个点，而纵向上每条直线被横向上的平行线截为n个点，所以平行四边形有

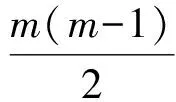
深度思考

“多种变式体验”需要建立联系.通过以上例子，我们发现让学生思维闪光的前提是：教师合理设计变式体验活动，将独立的材料按照一定的顺序进行排列、整合，同时巧妙地加以引导，这样才能让零散的思维聚集为有序的推理.

从独立走向整合.当“独立”的素材进行“整合”时，学生思维的深度也就自然而然地显现出来.在经历比较、分析之后，学生的思考变得有序、推断变得合理.这也正是教师希望达到的境界：直观的变式体验唤醒学生深入的思考，具体的感知提升为抽象的认识！

“让学生数学学习经历变式的过程”伴随着课改的步伐正与我们共同前行！体验数学变式学习的必要性，经历数学思想方法的概括过程，认清知识应用的广泛性及与生活的联系，才能更好地调动学生学习的主动性，使学生的数学思维不仅敏捷而且灵活，不仅深刻而且独创.

“心中悟出始知深.”变式可以简单，而思维必须深刻！结合以上5个例子的教学实践，笔者认为，如果平时能够充分钻研题目，注重变式教学，并运用于教学实际，让学生积极、主动地参与教学的全过程，调动和展示学生的思维，使学生在思维中形成一般性的“定势”，从而有利于培养学生的创造性思维，及大胆创新、勇于探索的精神，这样学生一定会收益匪浅，并真正把能力的培养落到实处.

[1] 罗增儒.初中数学奥林匹克[M].南宁：广西教育出版社，2001.

[2] 毛显勇.数学教学[M].上海：上海教育出版社，2004.

[3] 王万勇.数学大世界[M]．长春：世界图书出版公司，2003.

[4] 何乃忠.新课程有效操作教学解读[M].南宁：广西教育出版社，2008.