简议新课程中高中数学反思性学习
●
(余杭第二高级中学 浙江杭州 311100)
简议新课程中高中数学反思性学习
●刘芳丽
(余杭第二高级中学 浙江杭州 311100)
在教学中,笔者常会有这样的疑惑:这道题明明已经在课堂上讲过,学生也已心领神会,为什么在作业中却一错再错;明明是前两天才出现过的题目,今天为什么学生如此迷茫.作为学生,也挺纳闷:上课认真听、努力做笔记,为什么作业永远有不会的;很多题目今天会做,为什么过了一个晚上又不会了;做了那么多道题目,为什么成绩却每况愈下……
问题究竟出在哪里?
其实很多学生学数学犹如置身于迷雾中,有人带路,亦步亦趋;一旦独处,便会迷失方向.因此,在教学中,教师一定要教会学生学会反思自己的学习,从错误中成长,从似是而非中收获.
1 改错练习,激发反思
实践表明:认知体验最容易在重要的和困难的情境中产生,这种情境会引起学生思想的高度重视,使学生处于高度情绪唤醒之中.因此,要非常重视学生在解决数学问题时产生的错误.特别是有些错误的原因比较隐蔽、比较经典时,学生就容易产生反思认知体验.这时,教师就要指导学生进行反思,究其原因.
例如,在算法的学习过程中,书写算法一直是某些学生无法攻克的一个难点,经常会出现错误.笔者在教学中经常会把他们错误的程序整理出来,让大家一起反思.
例1已知分段函数
编写一个求该函数值的程序.
下面是学生编写的程序:
INPUTx
IF -4≤x≤-1 THEN
y=x2
ELSE
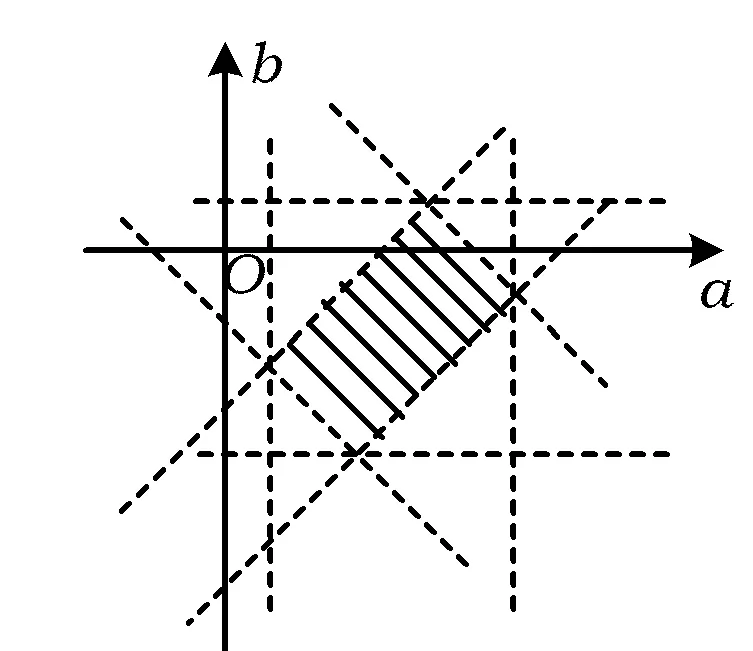
IF -1 y=x ELSE y=2x/x+1 END IF PRINTy END 分析这是一道很典型的有关条件语句的程序题.上述程序是学生中出现的错误程序.在课堂上,笔者把该程序写在黑板上,然后指导学生从书写错误和语句错误2个方面进行反思. 学生在逐句阅读后指出:程序中的不等式“-4≤x≤-1”应为“x>=-4 ANDx<=-1”;程序中的运算有特定的书写格式,“y=x2”应为“y=x^2”;比较隐蔽的书写错误为“y=2x/x+1”应改为“y=2x/(x+1)”. 接下来就是语句错误.很多学生一下子就能发现程序中少了一个“END IF”. “还有没有其他错误了呢?”很多学生觉得到此结束了.于是笔者开始带领大家一起分析“ELSE”中所隐含的x的取值范围:第1个“ELSE”中x的范围应为“x>-1或x<-4”,那么第2个呢?在笔者的提示之下,很多学生恍然大悟:原来第2个“ELSE”隐含着“x>2或x<-4”,而不仅仅代表“x>2”. 通过这道题的改错,学生明白编写程序要注意书写与语句的正确性,更重要的是要关注条件语句中“ELSE”所隐含的条件,更好地掌握“IF”语句. 有时候,通过正误解法的比较也可以让学生把握解题思路的本质. 例2已知-1 错解因为-1 1<2a<7,-5<2b<1, (1) 得 从而 正解令u=a+b,v=a-b,则 因为 -1 所以 故 但是很多学生根本就不明白为什么第1种解法错了,究竟错在哪里? 下面我们从线性规划的角度来解释第1种解法的错误所在: 图1 如图1所示,图中的阴影部分即为根据题设条件画出的可行域,而式(1)中表示的可行域为外面的正方形区域.由此可见,对条件进行处理后扩大了可行域的范围,因此也影响到了2a+3b的范围.这也是把“a+b”和“a-b”当成整体,采用第2种思路处理该问题的原因.通过这样的分析,不仅为学生创设了主动参与学习的问题情境,而且也能引导其养成经常反思自己的认知过程的习惯. 例3已知an=2n2-13n,从n=________起,an+1>an. 解法1可利用作差法解得n=2. 有些学生想到数列也是函数,利用二次函数的性质解得n=3,由此得到了矛盾的结论.这时,可引导学生进一步理解:数列是一种特殊的函数,它的图像是一些孤立的点,因此数列的单调性不等同于函数的单调性.从而指导学生要重视作业中所出现的错误,学会从错误中成长,因为有些错误可以带领我们进入一个新的理解境界. 有些学生做题总是拿不到满分,原因就是思维总存在漏洞.例如,已知f(x)=2+log2x,x∈[1,9],求y=[f(x)]2+f(x2)的最小值.很多学生一看题目就知道可以利用二次函数求最值,但却忽略了函数的定义域发生了变化.针对这一情况,教师可以先呈现错误的解法,让学生来发现漏洞,这样可以激发学生自觉进行反思,加深对解题思路的印象,完善解题思路中的缺陷. 与之类似的错误还有:很多学生一看到“ax2+bx+c”,就想当然地认为这是二次表达式,因此在解题过程中往往会遗忘对“a=0”的情况的讨论;一看到“集合A是集合B的子集”就忘了集合A有可能是空集的情况;一看到求直线方程就设“所求直线方程为y=kx+b”,也不管k是否存在.针对这些错误,多做几次纠错练习,就能不断地完善学生的解题思维.通过反思,可以找出错误的根源所在,可以发现知识或思维方法上的薄弱环节. 变式问题的解决有助于数学知识的灵活迁移.在教学中,要提倡一题多变、一题多解、多题一解的变式训练,精心创设一个符合学生认知规律,能激发学生求知热情的由浅入深、多层次、多变化的问题情境.在变式训练中,反思各种变式所共有的本质要素,揭示问题的条件与结论之间的内在联系及其隐含较深的知识规律. 例如,在算法的学习中,循环结构是算法一个重点和难点.很多学生一遇到循环结构就搞不清循环的次数及输出的结果该是什么. 例4编写求1×2×3×…×n>108的最小正整数n. n=1 T=1 WHILET<=10^8 T=T*n n=n+1 WEND PRINT________ END 思考:(1)在横线上到底该填“n”,“n+1”还是“n-1”呢? (2)循环体两行互换,横线又该填什么? (3)若要求“编写求1×2×3×…×n<108的最大正整数n”,则该程序又该怎么改写? 通过变式练习,加强学生对循环结构的训练,有利于他们总结反思循环结构的特征,攻克程序学习中的这一难点.这样的变式训练也有助于提高学生的学习效率. 同时,通过变式练习还可以区分似是而非的题目,使学生能有效地把握题目的本质,从而采取快捷并行之有效的解题方法. 例5在△ABC中,a,b,c分别为角A,B,C的对边,设f(x)=a2x2-(a2-b2)x-4c2. (2)当f(2)=0时,求角C的取值范围. 粗一看,这2个小题是一样的问题.做了之后,我们才发现,第(1)小题化简后得到的是两边两角的关系,用正弦定理解决该问题比较合适;而第(2)小题化简后得到的是三边关系,求一角,利用余弦定理更容易解决问题.整道题目的解决,诱使学生对正、余弦定理的区别使用进行反思. 数学中有很多定理都是从大胆猜想开始的,可以说猜想是数学思维中的火花.新课程中也对“合情推理”做出了要求,因此在教学中要不断引导学生进行大胆猜想,反思自己的认知过程.一旦猜想正确,学生就能处于一种成功的喜悦之中,并迸发出前所未有的学习热情;即使失败,学生也能从中得到创新的训练,能更自觉、主动地参与到学习中. 同时,合理联想也能帮助我们优化思维,形成新的知识结构.例如,在三角函数学习中,经常会碰到“sinx+cosx”、“sinx-cosx”、“sinxcosx”这3个式子.经过研究后发现这些式子是相互联系的,从这3个式子出发可以得到很多结论.从另一角度看,它们其实就是“a±b”及“ab”在三角函数中的具体表现.而“a±b”及“ab”在数学中还有很多表象:韦达定理、圆锥曲线中求弦长问题的策略、三角函数tan(α+β)的展开式中含有tanα+tanβ及tanαtanβ.既然这些都有相同的形式,在解题中也可以类似地处理,从而可以大大提高学习效率和解题的有效性. 在数学学习中,应重视知识的概括和提炼,反思探究知识的纵横联系,归纳出有更高抽象、概括和包容水平的观念,融会贯通并有序储存,形成活化的知识组块,优化知识结构. 图2 向量是高中数学中的一个有效的工具,尤其是几何问题.下面介绍如何用向量方法统一几何结论.在初中学过矩形的判定定理:“有一个角为直角的平行四边形是矩形”,“对角线长相等的平行四边形是矩形”,那么这2个判定定理有何联系呢? 例6如图2,求证: 利用向量证明后发现,原来这2个判定定理是一样的.同理,其余四边形的判定定理也都是异曲同工.通过这道题的训练可以强化向量数量积的应用,优化知识. 这样,知识点经过反思优化后就更容易记忆,解题时也可以尽量减少错误的出现. 知识在不断吸收的过程中会对原有的知识体系发生冲击,这时要特别反思究竟是原有的认识有问题,还是现在的知识有漏洞.例如,在初中一讲到切线,就认为是圆的切线,且与圆只有1个交点.但是随着学习的不断深入,尤其是经过曲线方程的学习,我们发现与曲线只有1个交点的直线可以是曲线的交线,而非切线.那么会不会有些曲线的切线与曲线的交点不止一个呢?答案是肯定的,例如曲线y=sinx与直线y=1.这样就完全颠覆了我们原有对切线的认识,使得对切线的认识更全面、更正确!因此,养成良好的反思习惯可以不断完善知识体系,达到事半功倍的效果. 除了引导学生对相关知识进行反思之外,还要引导学生全面反思学习的各个环节(预习、上课、作业、复习等),以及反思影响学习的非智力因素.对于作业中的错误要分析原因,寻根问底,及时订正,及时小结.另外,反思是一种持续的活动,并不是一时的心血来潮,它需要学习者有着学习的毅力和坚持不懈的精神.否则,反思就会流于形式,达不到预期的效果. 学习需要反思,没有反思的学习是不可能深刻的;学习是反思的,反思有助于学生主动探究,重构自己的经验,形成自己的解题策略和方式.南京师范大学涂荣豹教授也曾指出:“坚持反思性数学学习,才可能洞察数学活动的本质特征.”[2]因此,在教学中,要引导学生养成良好的反思习惯.曹才翰教授及张建跃教授也非常重视并倡导培养学生对学习过程的反思习惯,他们认为“培养学生对自己的学习过程进行反思的习惯,提高学生的思维与自我评价水平,这是提高学习效率、培养数学能力的行之有效的方法”[3].相信反思能帮助每位学生与数学“风雨同行”! [1] 中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003. [2] 涂荣豹.试论反思性数学学习[J].数学教育学报,2000(4):17-21. [3] 曹才翰,章建跃.数学教育心理学[M].北京:北京师范大学出版社,1999.

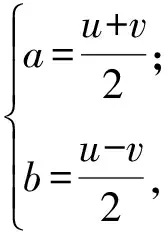
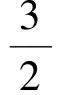

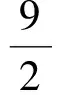
2 变式问题,诱导反思
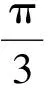
3 合理联想,促成反思
4 积极反思,优化知识

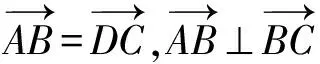
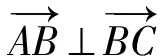
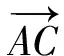



5 全面反思,持之以恒

